3.4 The Route to Spin(10) via Pati-Salam
In the last section, we showed how the Pati-Salam model answers two questions
about the Standard Model:
Why are quarks and leptons so similar? Why are left and right so
different?
We were able to describe leptons as a fourth color of quark, `white', and
treat right-handed and left-handed particles on a more equal footing.
Neither of these ideas worked on its own, but together, they made
a full-fledged extension of the Standard Model, much like 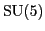 and
and
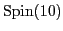 , but based on seemingly different principles.
, but based on seemingly different principles.
Yet thinking of leptons as `white' should be strangely familiar, not
just from the Pati-Salam perspective, but
from the binary code that underlies both the 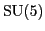 and the
and the
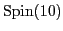 theories. There, leptons were indeed white: they all have
color
theories. There, leptons were indeed white: they all have
color
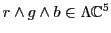 .
.
Alas, while 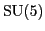 hints that leptons might be a fourth color, it does not
deliver on this. The quark colors
hints that leptons might be a fourth color, it does not
deliver on this. The quark colors
lie in a different irrep of 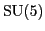 than does
than does
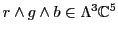 . So, leptons in the
. So, leptons in the 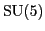 theory are white, but unlike
the Pati-Salam model, this theory
does not unify leptons with quarks.
theory are white, but unlike
the Pati-Salam model, this theory
does not unify leptons with quarks.
Yet 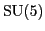 theory is not the only game in town when it comes to the binary
code. We also have
theory is not the only game in town when it comes to the binary
code. We also have
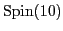 , which acts on the same vector space as
, which acts on the same vector space as
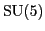 . As a representation of
. As a representation of
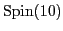 ,
,
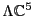 breaks up into just
two irreps: the even grades,
breaks up into just
two irreps: the even grades,
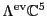 , which contain the left-handed
particles and antiparticles:
, which contain the left-handed
particles and antiparticles:
and the odd grades
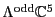 , which contain the right handed particles and
antiparticles:
, which contain the right handed particles and
antiparticles:
Unlike 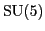 , the
, the
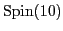 GUT really does unify
GUT really does unify
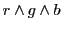 with the colors
with the colors 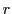 ,
, 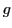 and
and 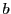 , because they
both live in the irrep
, because they
both live in the irrep
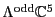 .
.
In short, it seems that the
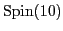 GUT, which we built as an
extension of the
GUT, which we built as an
extension of the 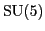 GUT, somehow managed to pick up
this feature of the Pati-Salam model.
How does
GUT, somehow managed to pick up
this feature of the Pati-Salam model.
How does
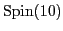 relate to Pati-Salam's gauge group
relate to Pati-Salam's gauge group
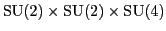 ,
exactly? In general, we only know there is a map
,
exactly? In general, we only know there is a map
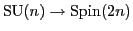 ,
but in low dimensions, there is much more, because some groups coincide:
,
but in low dimensions, there is much more, because some groups coincide:
What really stands out is this:
This brings out an obvious relationship between the Pati-Salam model and the
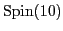 theory, because the inclusion
theory, because the inclusion
 lifts to the universal covers, so we get a homomorphism
lifts to the universal covers, so we get a homomorphism
A word of caution is needed here. While 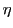 is the lift of an inclusion, it
is not an inclusion itself: it is two-to-one. This is because the universal
cover
is the lift of an inclusion, it
is not an inclusion itself: it is two-to-one. This is because the universal
cover
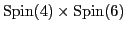 of
of
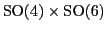 is a four-fold
cover, being a double cover on each factor.
is a four-fold
cover, being a double cover on each factor.
So we can try to extend the symmetries
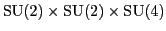 to
to
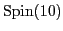 , though this can only work if the kernel of
, though this can only work if the kernel of 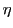 acts
trivially on the Pati-Salam representation.
What is this representation like? There is an obvious
representation of
acts
trivially on the Pati-Salam representation.
What is this representation like? There is an obvious
representation of
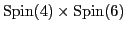 that extends to a
that extends to a
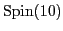 rep.
Both
rep.
Both 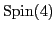 and
and 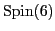 have Dirac spinor representations, so their
product
have Dirac spinor representations, so their
product
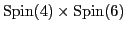 has a representation on
has a representation on
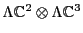 . And in fact, the obvious map
. And in fact, the obvious map
given by
is an isomorphism compatible with the actions of
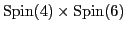 on these two spaces. More concisely, this square:
on these two spaces. More concisely, this square:
commutes.
We will prove this in a moment. First though, we must check that
this representation of
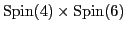 is secretly
just another name for the Pati-Salam representation of
is secretly
just another name for the Pati-Salam representation of
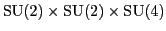 on the space we discussed in
Section 3.3:
on the space we discussed in
Section 3.3:
Checking this involves choosing an isomorphism between
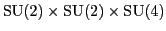 and
and
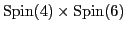 .
Luckily, we can choose one that works:
.
Luckily, we can choose one that works:
Theorem 4
.
There exists an isomorphism of Lie groups
and a unitary operator
that make this square commute:
where the left vertical arrow is the Pati-Salam representation
and the right one is a tensor product of Dirac spinor representations.
Proof. We can prove this in pieces, by separately finding
a unitary operator
that makes this square commute:
and a unitary operator
that make this square:
commute.
First, the 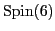 piece. It suffices to show that the Dirac spinor rep
of
piece. It suffices to show that the Dirac spinor rep
of
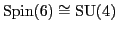 on
on
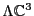 is isomorphic to
is isomorphic to
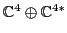 as a rep of
as a rep of
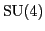 . We start with the action of
. We start with the action of 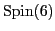 on
on
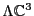 . This breaks up
into irreps:
. This breaks up
into irreps:
called the left-handed
and right-handed Weyl spinors, and these are dual to each
other because 6 = 2 mod 4, by a theorem that can be found
in Adams' lectures [1]. Call these representations
Since these reps are dual, it suffices just to consider one of them, say
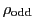 .
.
Passing to Lie algebras, we have a homomorphism
Homomorphic images of semisimple Lie algebras are semisimple, so the image of
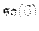 must lie entirely in
must lie entirely in
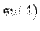 . In fact
. In fact
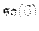 is simple, so this
nontrivial map must be an injection
is simple, so this
nontrivial map must be an injection
and because the dimension is 15 on both sides, this map is also
onto. Thus
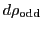 is an isomorphism of Lie algebras, so
is an isomorphism of Lie algebras, so
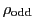 is an isomorphism of the simply connected Lie
groups
is an isomorphism of the simply connected Lie
groups 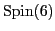 and
and 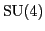 :
:
Furthermore, under this isomorphism
as a representation of
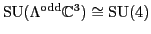 .
Taking duals, we obtain an isomorphism
.
Taking duals, we obtain an isomorphism
Putting these together, we get an isomorphism
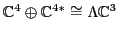 that makes this square commute:
that makes this square commute:
which completes the proof for 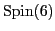 .
.
Next, the 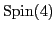 piece. It suffices
to show that the spinor rep
piece. It suffices
to show that the spinor rep
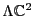 of
of
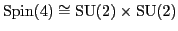 is isomorphic to
is isomorphic to
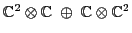 as a rep of
as a rep of
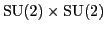 . We start with the action of
. We start with the action of 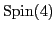 on
on
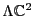 . This
again breaks up into irreps:
. This
again breaks up into irreps:
Again we call these representations
First consider
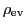 . Passing to Lie algebras, this gives
a homomorphism
. Passing to Lie algebras, this gives
a homomorphism
Homomorphic images of semisimple Lie algebras are semisimple, so the image of
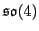 must lie entirely in
must lie entirely in
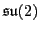 . Similarly,
. Similarly,
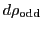 also takes
also takes
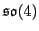 to
to
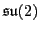 :
:
and we can combine these maps to get
which is just the derivative of 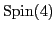 's representation on
's representation on
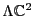 .
Since this representation is faithful, the map
.
Since this representation is faithful, the map
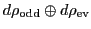 of Lie
algebras is injective. But the dimensions of
of Lie
algebras is injective. But the dimensions of
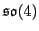 and
and
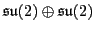 agree, so
agree, so
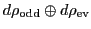 is also onto. Thus it is an isomorphism
of Lie algebras. This implies that
is also onto. Thus it is an isomorphism
of Lie algebras. This implies that
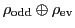 is an isomorphism of of
the simply connected Lie groups
is an isomorphism of of
the simply connected Lie groups 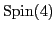 and
and
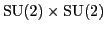
under which
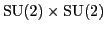 acts on
acts on
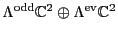 . The
left factor of
. The
left factor of 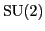 acts irreducibly on
acts irreducibly on
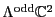 , which the second
factor is trivial on. Thus
, which the second
factor is trivial on. Thus
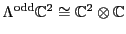 as a rep of
as a rep of
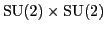 . Similarly,
. Similarly,
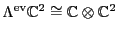 as a rep of this group. Putting these together,
we get an isomorphism
as a rep of this group. Putting these together,
we get an isomorphism
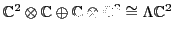 that makes this square commute:
that makes this square commute:
which completes the proof for 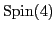 .
. 
In the proof of the preceding theorem, we merely showed that there
exists an isomorphism
making the square commute. We did not say exactly what 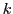 was.
In the proof, we built it after quietly choosing
three unitary operators, giving these isomorphisms:
was.
In the proof, we built it after quietly choosing
three unitary operators, giving these isomorphisms:
Since the remaining map
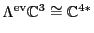 is determined by
duality, these three operators determine
is determined by
duality, these three operators determine 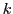 , and they also
determine the Lie group isomorphism
, and they also
determine the Lie group isomorphism 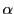 via the construction in our proof.
via the construction in our proof.
There is, however, a specific choice for these unitary operators that we
prefer, because this choice makes the particles in the Pati-Salam
representation
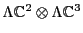 look almost exactly like
those in the
look almost exactly like
those in the 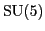 representation
representation
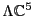 .
.
First, since
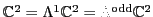 is spanned by
is spanned by 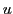 and
and
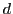 , the (left-handed) isospin states of the Standard Model, we really ought
to identify the left-isospin states
, the (left-handed) isospin states of the Standard Model, we really ought
to identify the left-isospin states 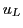 and
and 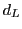 of the Pati-Salam model
with these. So, we should use this unitary operator:
of the Pati-Salam model
with these. So, we should use this unitary operator:
Next, we should use this unitary operator for right-isospin states:
Why? Because the right-isospin up particle is the right-handed neutrino
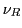 , which corresponds to
, which corresponds to
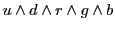 in the
in the 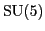 theory, but
theory, but 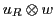 in the Pati-Salam model. This suggests that
in the Pati-Salam model. This suggests that 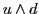 and
and 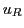 should be identified.
should be identified.
Finally, because
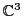 is spanned by the colors
is spanned by the colors 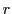 ,
, 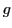 and
and 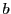 , while
, while
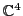 is spanned by the colors
is spanned by the colors 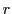 ,
, 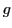 ,
, 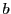 and
and 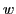 , we really ought
to use this unitary operator:
, we really ought
to use this unitary operator:
Dualizing this, we get the unitary operator
These choices determine the unitary operator
With this specific choice of 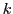 , we can combine the commutative squares
built in Theorems 3 and
4:
, we can combine the commutative squares
built in Theorems 3 and
4:
to obtain the following result:
Theorem 5
.
Taking
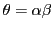 and
and 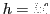 , the
following square commutes:
where the left vertical arrow is the Standard Model representation and
the right one is a tensor product of Dirac spinor representations.
, the
following square commutes:
where the left vertical arrow is the Standard Model representation and
the right one is a tensor product of Dirac spinor representations.
The map 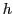 , which tells us how to identify
, which tells us how to identify 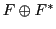 and
and
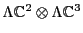 , is given by applying
, is given by applying 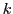 to the `Pati-Salam code' in
Table 5. This gives a binary code for the
Pati-Salam model:
to the `Pati-Salam code' in
Table 5. This gives a binary code for the
Pati-Salam model:
Table 6:
Pati-Salam binary code for first-generation fermions, where 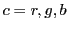 and
and
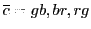 .
.
| The Binary Code for Pati-Salam |
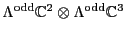 |
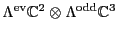 |
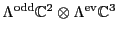 |
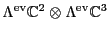 |
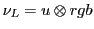 |
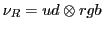 |
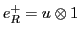 |
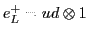 |
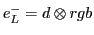 |
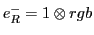 |
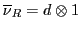 |
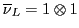 |
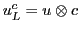 |
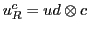 |
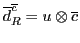 |
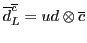 |
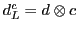 |
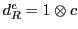 |
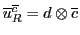 |
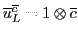 |
|
We have omitted wedge product symbols to save space. Note that if we apply the
obvious isomorphism
given by
then the above table does more than
merely resemble Table 4, which gives the
binary code for the 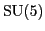 theory. The two tables become
identical!
theory. The two tables become
identical!
This fact is quite intriguing. We will explore its meaning
in the next section. But first, let us start by relating the
Pati-Salam model to the
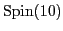 theory:
theory:
Theorem 6
.
The following square commutes:
where the right vertical arrow is the Dirac spinor representation,
the left one is the tensor product of Dirac spinor representations,
and
is the homomorphism lifting the inclusion of
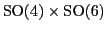 in
in
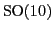 .
.
Proof. At the Lie algebra level, we have the inclusion
by block diagonals, which is also just the differential of the inclusion
 at the Lie group level. Given how the
spinor reps are defined in terms of creation and annihilation operators, it is
easy to see that
at the Lie group level. Given how the
spinor reps are defined in terms of creation and annihilation operators, it is
easy to see that
commutes, because 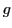 is an
intertwining operator between representations
of
is an
intertwining operator between representations
of
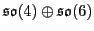 .
That is because the
.
That is because the
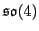 part only acts on
part only acts on
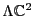 , while the
, while the
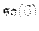 part only acts on
part only acts on
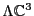 .
.
But these Lie algebras act by skew-adjoint operators, so really
commutes. Since the
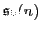 's and their direct sums are semisimple, so are
their images. Therefore, their images live in the semisimple part of the
unitary Lie algebras, which is just another way of saying the special unitary
Lie algebras. We get that
's and their direct sums are semisimple, so are
their images. Therefore, their images live in the semisimple part of the
unitary Lie algebras, which is just another way of saying the special unitary
Lie algebras. We get that
commutes, and this gives a commutative square in the world of
simply connected Lie groups:
This completes the proof. 
This result shows us how to reach the
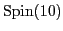 theory, not
through the
theory, not
through the 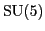 theory, but through the Pati-Salam model.
For physics texts that treat this issue, see for example
Zee [40] and Ross [31].
theory, but through the Pati-Salam model.
For physics texts that treat this issue, see for example
Zee [40] and Ross [31].
2010-01-11
![]() and
and
![]() , but based on seemingly different principles.
, but based on seemingly different principles.
![]() and the
and the
![]() theories. There, leptons were indeed white: they all have
color
theories. There, leptons were indeed white: they all have
color
![]() .
.
![]() hints that leptons might be a fourth color, it does not
deliver on this. The quark colors
hints that leptons might be a fourth color, it does not
deliver on this. The quark colors
![]() theory is not the only game in town when it comes to the binary
code. We also have
theory is not the only game in town when it comes to the binary
code. We also have
![]() , which acts on the same vector space as
, which acts on the same vector space as
![]() . As a representation of
. As a representation of
![]() ,
,
![]() breaks up into just
two irreps: the even grades,
breaks up into just
two irreps: the even grades,
![]() , which contain the left-handed
particles and antiparticles:
, which contain the left-handed
particles and antiparticles:
![]() GUT, which we built as an
extension of the
GUT, which we built as an
extension of the ![]() GUT, somehow managed to pick up
this feature of the Pati-Salam model.
How does
GUT, somehow managed to pick up
this feature of the Pati-Salam model.
How does
![]() relate to Pati-Salam's gauge group
relate to Pati-Salam's gauge group
![]() ,
exactly? In general, we only know there is a map
,
exactly? In general, we only know there is a map
![]() ,
but in low dimensions, there is much more, because some groups coincide:
,
but in low dimensions, there is much more, because some groups coincide:

![]() theory, because the inclusion
theory, because the inclusion
![]() lifts to the universal covers, so we get a homomorphism
lifts to the universal covers, so we get a homomorphism
![]() to
to
![]() , though this can only work if the kernel of
, though this can only work if the kernel of ![]() acts
trivially on the Pati-Salam representation.
What is this representation like? There is an obvious
representation of
acts
trivially on the Pati-Salam representation.
What is this representation like? There is an obvious
representation of
![]() that extends to a
that extends to a
![]() rep.
Both
rep.
Both ![]() and
and ![]() have Dirac spinor representations, so their
product
have Dirac spinor representations, so their
product
![]() has a representation on
has a representation on
![]() . And in fact, the obvious map
. And in fact, the obvious map
![\begin{displaymath}
\xymatrix{
{\rm Spin}(4) \times {\rm Spin}(6) \ar[r]^-\eta \...
...3) \ar[r]^-{{\rm U}(g)} & {\rm U}(\Lambda {\mathbb C}^5) \\
}
\end{displaymath}](img661.png)
![]() is secretly
just another name for the Pati-Salam representation of
is secretly
just another name for the Pati-Salam representation of
![]() on the space we discussed in
Section 3.3:
on the space we discussed in
Section 3.3:
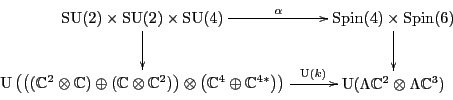
![\begin{displaymath}
\xymatrix{
{\rm SU}(2) \times {\rm SU}(2) \ar[r]^-\sim \ar[d...
...thbb C}^2) \ar[r]^-\sim & {\rm U}(\Lambda {\mathbb C}^2) \\
}
\end{displaymath}](img667.png)
![\begin{displaymath}
\xymatrix{
{\rm SU}(4) \ar[r]^\sim \ar[d] & {\rm Spin}(6) \a...
...b C}^{4*}) \ar[r]^-\sim & {\rm U}(\Lambda {\mathbb C}^3) \\
}
\end{displaymath}](img669.png)
![]() piece. It suffices to show that the Dirac spinor rep
of
piece. It suffices to show that the Dirac spinor rep
of
![]() on
on
![]() is isomorphic to
is isomorphic to
![]() as a rep of
as a rep of
![]() . We start with the action of
. We start with the action of ![]() on
on
![]() . This breaks up
into irreps:
. This breaks up
into irreps:
![\begin{displaymath}
\xymatrix{
{\rm Spin}(6) \ar[d] \ar[r]^\rho_{\rm{odd}}& {\rm...
...}^3) \ar[r] & {\rm U}({\mathbb C}^4 \oplus {\mathbb C}^{4*})
}
\end{displaymath}](img684.png)
![]() piece. It suffices
to show that the spinor rep
piece. It suffices
to show that the spinor rep
![]() of
of
![]() is isomorphic to
is isomorphic to
![]() as a rep of
as a rep of
![]() . We start with the action of
. We start with the action of ![]() on
on
![]() . This
again breaks up into irreps:
. This
again breaks up into irreps:
![]() . Passing to Lie algebras, this gives
a homomorphism
. Passing to Lie algebras, this gives
a homomorphism
![\begin{displaymath}
\xymatrix{
{\rm Spin}(4) \ar[d] \ar[r]^-{\rho_{\rm{ev}}\oplu...
... \otimes {\mathbb C}\oplus {\mathbb C}\otimes {\mathbb C}^2)
}
\end{displaymath}](img704.png)
![]() look almost exactly like
those in the
look almost exactly like
those in the ![]() representation
representation
![]() .
.
![]() is spanned by
is spanned by ![]() and
and
![]() , the (left-handed) isospin states of the Standard Model, we really ought
to identify the left-isospin states
, the (left-handed) isospin states of the Standard Model, we really ought
to identify the left-isospin states ![]() and
and ![]() of the Pati-Salam model
with these. So, we should use this unitary operator:
of the Pati-Salam model
with these. So, we should use this unitary operator:
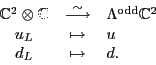
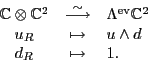
![]() is spanned by the colors
is spanned by the colors ![]() ,
, ![]() and
and ![]() , while
, while
![]() is spanned by the colors
is spanned by the colors ![]() ,
, ![]() ,
, ![]() and
and ![]() , we really ought
to use this unitary operator:
, we really ought
to use this unitary operator:
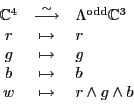
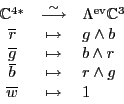
![\begin{displaymath}
\xymatrix{
{G_{\mbox{\rm SM}}}\ar[r]^-{\beta} \ar[d]
& {\rm...
...ght) \ar[r]^-{{\rm U}(k)}
& {\rm U}(\Lambda {\mathbb C}^5)
}
\end{displaymath}](img716.png)
![\begin{displaymath}
\xymatrix{
{G_{\mbox{\rm SM}}}\ar[r]^-\theta \ar[d] & {\rm...
...}(\Lambda {\mathbb C}^2 \otimes \Lambda {\mathbb C}^3) \\
}
\end{displaymath}](img719.png)
![]() , which tells us how to identify
, which tells us how to identify ![]() and
and
![]() , is given by applying
, is given by applying ![]() to the `Pati-Salam code' in
Table 5. This gives a binary code for the
Pati-Salam model:
to the `Pati-Salam code' in
Table 5. This gives a binary code for the
Pati-Salam model:
![]() theory:
theory:
![\begin{displaymath}
\xymatrix{
{\rm Spin}(4) \times {\rm Spin}(6) \ar[r]^-\eta \...
...3) \ar[r]^-{{\rm U}(g)} & {\rm U}(\Lambda {\mathbb C}^5) \\
}
\end{displaymath}](img661.png)
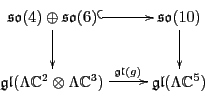
![\begin{displaymath}
\xymatrix{
{\mathfrak{so}}(4) \oplus {\mathfrak{so}}(6) \ar@...
...thbb C}^3) \ar[r]^-{\u (g)} & \u (\Lambda {\mathbb C}^5) \\
}
\end{displaymath}](img744.png)
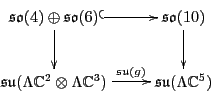
![\begin{displaymath}
\xymatrix{
{\rm Spin}(4) \times {\rm Spin}(6) \ar[r]^-\eta \...
...}^3) \ar[r]^-{{\rm SU}(g)} & {\rm SU}(\Lambda {\mathbb C}^5)
}
\end{displaymath}](img747.png)
![]() theory, not
through the
theory, not
through the ![]() theory, but through the Pati-Salam model.
For physics texts that treat this issue, see for example
Zee [40] and Ross [31].
theory, but through the Pati-Salam model.
For physics texts that treat this issue, see for example
Zee [40] and Ross [31].