
Happy New Year!
The Earth has successfully completed another revolution about the Sun! This is a traditional excuse for a moment of reflection, so I'll try that.
It's been an interesting and stressful year for me. I'm struggling to do some more practical things for the health of our planet. I believe global warming is a serious problem and we're facing a mass extinction event. I can't just sit around. But my love for the beauty of pure math and theoretical physics keeps pulling me back to the things I used to think about. I feel torn and frustrated.
With my pals at the Azimuth Project, we've reached the point of understanding a bit about El Niño prediction — I gave a talk about this to about 1000 people at the Neural Information Processing Seminar, a big annual conference on machine learning. We made some good progress. But we've only just dipped our toes into a very deep subject. To go further I'd need to learn a lot more, get serious about programming, and start attending the annual conference on Climate Informatics. I'd need to get better at working with folks in the Azimuth Project, and pull more experts into it. And most of all: I'd need to think harder about climate science and the art of prediction, and come up with some new ideas.
By comparison, it seems easy to come up with new ideas in pure math and theoretical physics — because I spent decades doing it. Unfortunately, it feels a bit pointless. I don't think the world urgently needs to understand more about the fundamental laws of physics, not right now. Someday it will be important. But fundamental physics doesn't hold the 'magic bullet' for the problems we face today. And anyway, we've already got a lot of very smart people banging their heads against that wall. We need something a bit different. I'm in a lucky position where I can afford to thrash around trying to figure out what that is. If 1000 of us try, some will succeed, and we may do a bit better finding our way through the ecological bottleneck.
That's what I tell myself, anyway. But I also just love pure math regardless of whether it's good for anything. So right now I'm pursuing it as a kind of 'hobby'. It helps me relax. I've stepped aside from the great mathematical challenge of our time — developing the theory of infinity-categories and the new world of math this opens up. Instead, I'm thinking about 'exceptional structures' in algebra, and their role in physics: things like the octonions, the group called E8, and the Leech lattice. I've put enough time into these over the years that I can come up with cute ideas without a massive investment of effort.... thanks to help from Greg Egan, who is great at proving or disproving my conjectures.
As a kind of middle road, I'm also working with my grad students on 'network theory' — basically, applying category theory to comlex systems made of interacting parts, as we see in biology, chemistry, electrical engineering, and the like. This is not instantly useful; it will take years to develop. But I have a good feeling about it! This might be a place where fancy abstract math can do some good.
So I guess it's a three-pronged approach to life. It gets to be a bit much at times! And then there's the job I actually get paid for: teaching. I may be doing too many things to do any of them well.
But I'm rarely bored. When I was a kid, I was often bored. I didn't know how to do the cool things I dreamt of doing. I hated it. Those days are gone. I'm very happy about that.
In case you're wondering, the image here is the Higman-Sims graph, an exceptional structure lurking in the Leech lattice, animated by David Madore. He writes:
The Higman-Sims graph is the unique graph with 100 vertices such that each is adjacent to 22 others and no two adjacent vertices have a common neighbor (i.e., the graph has no triangle) and any two non-adjacent vertices have exactly six common neighbors. It has 88704000 automorphism, forming an extension of 2 by the unique simple group of order 44352000 (the Higman-Sims group, a sporadic group).The Higman-Sims graph occurs inside the 24-dimensional Leech lattice (if X,Y,Z are Leech lattice points at distances 3,3,2 from each other, then there are 100 Leech lattice points at distance 2,2,2 from X,Y,Z, and if we connect those at distance 3 from another, we obtain the Higman-Sims graph).
This animation displays various orthogonal projections of the Higman-Sims graph inside the Leech lattice, chosen so as to reveal an 11-fold symmetry (there is only one conjugacy class of order 11 in the Conway group 70, which is in the Higman-Sims group).
An adult male grizzly bear can stand 3 meters tall (almost 10 feet) on its hind legs. A big one can weigh 360 kilograms (almost 800 pounds).
But that's not the really dangerous animal in this picture. A human being won this contest — with a gun.
Luckily it was a dart gun. This bear, near Vancouver, is sedated, about to be tagged by scientists. It will be fine, losing only a bit of its dignity.
Derrick Jensen wrote a book Thought to Exist in the Wild: Awakening from the Nightmare of Zoos. Here are some quotes:
The bear takes seven steps, her claws clicking on concrete. She dips her head, turns, and walks toward the front of the cage. Another dip, another turn, another three steps. When she gets back to where she started, she begins all over. This is what's left of her life.For more of Derrick Jensen's book, see:Outside the cage, people pass by on a sidewalk. Parents stop strollers until they realize there's nothing here to see. A pair of teenagers approach, wearing Walkmans and holding hands; one glance inside is enough, and they're off to the next cage. Still the bear paces; three steps, head dip, turn.
My fingers are wrapped tightly around the metal railing outside the enclosure. I notice they're sore. I look at the silver on the bear.s back, the concave bridge of her nose. I wonder how long she's been here. I release the rail, and as I walk away, the rhythmic clicking of claws on concrete slowly fades.
Unfortunately most of us by now have been to enough zoos to be familiar with the archetype of the creature who has been driven insane by confinement: the bear pacing a precise rectangle; the ostrich incessantly clapping his bill; the elephants rhythmically swaying. But the bear I describe is no archetype. She is a bear. She is a bear who, like all other bears, at one time had desires and preferences all her own, and who may still, beneath the madness.
Or at this point she may not.
[...]
If you see an animal in a zoo, you are in control. You can come, and you can go. The animal cannot. She is at your mercy; the animal is on display for you.
In the wild, the creature is there for her own purposes. She can come, and she can go. So can you. Both of you can display as much of yourselves to the other as you wish. It is a meeting of equals. And that makes all the difference in the world.
One of the great delights of living far from the city is getting to know my nonhuman neighbors — the plants, animals, and others who live here. Although we've occasionally met by chance, I've found that it is usually the animals who determine how and when they reveal themselves to me. The bears, for example, weren't shy, showing me their scat immediately and their bodies soon after, standing on hind legs to put muddy paws on windows and look inside; or offering glimpses of furry rumps that disappeared quickly whenever I approached on a path through the forest; or walking slowly like black ghosts in the deep gray of predawn. Though I am used to their being so forward, it is always a gift when they reveal themselves, as one did recently when he took a swim in the pond in front of me.
Robins, flickers, hummingbirds, and phoebes all present themselves, too. Or rather, like the bear, they present the parts of themselves they want seen. I see robins often, and a couple of times I've seen fragments of blue eggshells long after the babies have left, but I've never seen their nests.
These encounters — these introductions — are on terms chosen by those who were on this land long before I was: they choose the time, place, and duration of our meetings. Like my human neighbors and friends, they show me what they want of themselves, when they want to show it, how they want to show it, and for that I am glad. To demand they show me more — and this is as true for nonhumans as it is for humans — would be unconscionably rude. It would destroy any potential our relationship may once have had. It would be unneighborly.
I am fully aware that even a young bear can kill me. I am also fully aware that humans have coexisted with bears and other wild animals for tens of thousands of years. Nature is not scary. It is not a den of fright and horrors. For almost all of human existence, it has been home, and the wild animals have been our neighbors.
Right now, worldwide, more than 1 million people die each year in road accidents. In the United States alone, there are about forty-two thousand traffic fatalities a year. Yet I am not afraid of cars — though perhaps I should be. Around the world, nearly 2 million people per year are killed through direct violence by other people. Almost 5 million people die each year from smoking. And how many people do bears kill? About one every other year in all of North America.
We are afraid of the wrong things.
[...]
I'm at a zoo. Everywhere I see consoles atop small stands. Each console has a cartoonish design aimed at children, and each has a speaker with a button. When I push the button, I hear a voice begin the singsong: "All the animals in the zoo are eagerly awaiting you". The song ends by reminding the children to be sure to "get in on the fun".
I look at the concrete walls, the glassed-in spaces, the moats, the electrified fences. I see the expressions on the animals' faces, so different from the expressions of the wild animals I've seen. The central conceit of the zoo, and in fact the central conceit of this whole culture, is that all of these "others" have been placed here for us, that they do not have any existence independent of us, that the fish in the oceans are waiting there for us to catch them, that the trees in the forests stand ready for us to cut them down, that the animals in the zoo are there for us to be entertained by them.
It may be flattering to believe that everything is here to serve you, but in the real world, where real creatures exist and real creatures suffer, it's narcissistic and dangerous to pretend nobody matters but you.
I got the photo from Sean Sparling's Twitter feed. I do not know who took it.

The Pythagorean theorem says the sum of the squares of the sides of a right triangle is the square of the hippopotamus. For example, there's a right triangle with sides of length 3, 4, and 5, since $$9 + 16 = 25$$ so $$3^2 + 4^2 = 5^2 $$ We call three integers with these properties a Pythagorean triple. There are infinitely many! For example, the next ones are $$ \begin{array}{ccc} 5^2+ 12^2= 13^2 &\qquad & (25 + 144 = 169) \\ \\ 8^2+ 15^2= 17^2 & & (64 + 225 = 289) \end{array} $$ There's a nice recipe to get all the Pythagorean triples! Just take integers \(n \lt m\) and let $$ \begin{array}{ccl} a &=& m^2- n^2 \\ b &=& 2mn \\ c &=& m^2+ n^2 \end{array} $$ Then you get $$ a^2+ b^2= c^2 $$
This doesn't give all the Pythagorean triples yet — but you can get the rest by taking \(a, b,\) and \(c\) and multiplying them all by the same number.
All this has been known for a long time — Euclid wrote about it around 300 BC. There's a lot more to say, but not now! Yesterday the guy who fixes my computers, David Scharffenberg, told me that $$ 3^3 + 4^3 + 5^3 = 6^3 $$ That's great! It looks like a generalization of $$ 3^2+ 4^2 = 5^2$$ But it's not really a generalization in any way that I know. As far as I know, this equation is just a wonderfully cute, meaningless coincidence. I could be wrong. But in particular, $$ 3^4 + 4^4 + 5^4 + 6^4 \ne 7^4 $$
When is the sum of 3 cubes a cube? I don't know, but there's a conjecture saying that any number except for those of the form \(9k+4\) and \(9k-4\) is the sum of 3 cubes.
Puzzle 1: Why can't numbers of the form \(9k+4\) or \(9k-4\) for some integer \(k\) be written as the sum of 3 cubes of integers?
Puzzle 2: The solution to Puzzle 1 involves working modulo 9. Why can't you get more constraints by working modulo other numbers?
For example, 29 is the sum of 3 cubes: $$ 3^3 + 1^3 + 1^3 = 29 $$
But cubes can be negative! This makes it harder to find all the solutions. For example, we also have $$ 4^3 + (-2)^3 + (-3)^3 = 29 $$
So, was only rather recently that the number 30 was shown to be the sum of 3 cubes: $$ (-283059965)^3 + (-2218888517)^3 + 2220422932^3 = 30 $$ Pine, Yarbrough, Tarrant, and Beck discovered this in 1999 following an approach suggested by Noam Elkies.
It's still not known if the number 33 is a sum of 3 cubes! But don't bother looking for solutions where the absolute value of one of the three numbers being cubed is less than 100 trillion, because there aren't any.
For more see:
On Dec. 31, 2003, I took a bus from Germany to Macedonia. When we arrived, my nightmare began. Macedonian agents confiscated my passport and detained me for 23 days. I was not allowed to contact anyone, including my wife.Khaled El-Masri wrote this back in 2005, and I added it to my collection of posts about the US-run torture program:At the end of that time, I was forced to record a video saying I had been treated well. Then I was handcuffed, blindfolded and taken to a building where I was severely beaten. My clothes were sliced from my body with a knife or scissors, and my underwear was forcibly removed. I was thrown to the floor, my hands pulled behind me, a boot placed on my back. I was humiliated.
Eventually my blindfold was removed, and I saw men dressed in black, wearing black ski masks. I did not know their nationality. I was put in a diaper, a belt with chains to my wrists and ankles, earmuffs, eye pads, a blindfold and a hood. I was thrown into a plane, and my legs and arms were spread-eagled and secured to the floor. I felt two injections and became nearly unconscious. I felt the plane take off, land and take off. I learned later that I had been taken to Afghanistan.
In Afghanistan, he was interrogated in the Salt Pit, a CIA-run 'black site' shown in the picture above. We are now learning more about this place.
There, I was beaten again and left in a small, dirty, cold concrete cell. I was extremely thirsty, but there was only a bottle of putrid water in the cell. I was refused fresh water.He was interrogated, force-fed, lost 60 pounds. His requests to see a lawyer were ignored. Eventually he was blindfolded, handcuffed, chained to an airplane seat, and taken to Albania, where he was left in the mountains. Eventually he made it back to his home in Germany.That first night I was taken to an interrogation room where I saw men dressed in the same black clothing and ski masks as before. They stripped and photographed me, and took blood and urine samples. I was returned to the cell, where I would remain in solitary confinement for more than four months.
His crime? His name resembled that of the terror suspect Khalid al-Masri.
In 2006 as U.S. Federal District Judge dismissed a lawsuit he filed against the CIA, stating that a public trial would "present a grave risk of injury to national security." A Court of Appeals also dismissed the case, and in 2008 so did the U.S. Supreme Court.
In the newly released U.S. Senate report, a supervisor is quoted as saying the Salt Pit was "good for interrogations because it is the closest thing ... to a dungeon." According to the Los Angeles Times:
Guards and interrogators tiptoed through the darkness, carrying headlamps to count detainees packed into two dozen cells. Their lights illuminated prisoners hanging from overhead bars, next to buckets on the floor to catch their waste. One hung there for 17 days.Another detainee "looked like a dog that had been kenneled," wrote an interrogator. "When the doors to their cells were opened, they cowered," according to CIA documents quoted in the report.
Indeed, reports of sleep and sensory deprivation; of nudity and unhealthful, unsanitary food; of cold showers and ice buckets; and of rough takedowns and mock executions never were reported to supervisors.
The moral? I don't have a moral. But it's curious: anyone in the US who cared has known the rough outlines of what we've been doing for at least 12 years. Read my posts! Yet now some people are acting surprised. Where were they back then?

Leibniz based his approach to calculus on infinitesimals - numbers that are bigger than zero but smaller than 1/2, 1/3, 1/4, ... and so on. Many people were uncomfortable with these, so they figured out how to do calculus without infinitesimals. That's how it's usually taught now.
But it turns out you can do calculus with infinitesimals in a perfectly rigorous way... and in some ways, it's easier! Here's a free online textbook that teaches calculus this way:
The picture here is from this book. There's a tiny little infinitesimal number \(\epsilon\), pronounced 'epsilon'. And \(1/\epsilon\) is infinitely big! These aren't 'real numbers' in the usual sense. Sometimes they're called hyperreal numbers.
You can calculate the derivative, or rate of change, of a function \(f\) by doing $$ \frac{f(x+\epsilon) - f(x)}{\epsilon} $$ and then at the end throwing out terms involving \(\epsilon\). For example, suppose $$ f(x) = x^2 $$ Then to compute its derivative we do $$ \frac{(x+\epsilon)^2 - x^2}{\epsilon} $$ Working this out, we get $$ \frac{x^2 + 2 \epsilon x + \epsilon^2 - x^2}{\epsilon} = \frac{2\epsilon x + \epsilon^2}{\epsilon} = 2 x + \epsilon $$ Then, at the end, we throw out the term involving \(\epsilon\). So, we get \(2 x \) This is the rate of change of the function \(x^2 \).
The book will teach you calculus this way, from scratch. If you had trouble understanding 'limits' in calculus, you might prefer this way. Or, you might just enjoy seeing another approach.
The details of this subject are infinitely interesting, but I'll just say an infinitesimal amount. In 1961 the logician Abraham Robinson showed that hyperreal numbers are just as consistent as ordinary real numbers, and that the two systems are compatible in a certain precise sense. In 1976, Jerome Keisler, a student of the famous logician Tarski, published this elementary textbook that teaches calculus using hyperreal numbers.
Now it's free, with a Creative Commons copyright!

If you ever had a spirograph, or even better if you never had one: now there's a one on your web browser! It's called Inspirograph.
It's easy to use. You just move one gear around the other using your mouse (or finger). I still prefer the actual spirograph: working with actual physical tools is a much more immersive experience than twiddling a computer. People are getting starved for contact with interesting matter. But not everyone has access to a spirograph!
It's written using TypeScript - a typed superset of JavaScript that compiles to plain JavaScript.
What if you look for shapes that are as symmetrical as Platonic solids, but where all the faces are stars? Then you'll find this.
If you look carefully, you'll see lots of 5-pointed stars. Each one is a regular pentagram &mdash a 5-pointed star whose corners are a regular pentagon. Each one touches 5 others at each corner, in exactly the same way. So, it's as regular as you might want.
But it's funny in some ways. First, the faces are stars instead of regular polyhedra. Second, the faces intersect each other: that's why you don't see all of any star.
There are 2 polyhedra whose faces are all regular stars, with each face just like every other and each vertex like every other.
This particular one is called the small stellated dodecahedron, because if you remove all the pyramid-shaped pieces you're left with a dodecahedron! Each star lies in the same plane as one of this dodecahedron's faces. So, there are 12 stars in this shape.
On the other hand, the sharp points of this shape form the corners of an invisible icosahedron! So, there are 20 sharp points.
Puzzle: how many edges does this shape have?
This shape can be seen in a floor mosaic in the Basilica of Saint Mark in Venice, built in 1430. It was rediscovered by Kepler in his work Harmonice Mundi in 1619. This book, about the "harmonies of the world", is an amazing mix of geometry, astronomy and music theory — a mystical warmup for his later breakthroughs on the orbits of the planets.
Much later, Escher made himself a wood model of the small stellated dodecahedron, which he drew in two woodcuts called Order and Chaos.
Besides the small stellated dodecahedron, there's another regular polyhedron with star faces: the great stellated dodecahedron. These two and their duals are called the Kepler–Poinsot polyhedra.
While the Kepler–Poinsot polyhedra are beautiful, I've avoided studying them because I don't see how they fit into the theory of Coxeter groups &mdash the study of discrete symmetries that connects Platonic solids, Archimedean solids and hyperbolic honeycombs to deeper strands of math like Lie theory, the study of continuous symmetries. I've been afraid these shapes are merely cute, not deep.
Maybe it's time to find out.
For more, see:
This shape is called a ditrigonal dodecadodecahedron. The term 'ditrigonal' is a bit hard to explain. But it's called a 'dodecadodecahedron' because it has 12 pentagons and 12 pentagrams as faces.
It's easy to see the pentagrams - they're the red stars. But what about the 12 pentagons? That's the yellow stuff.
Do you see how to get this yellow stuff from 12 pentagons? At first I didn't see how. Now I do. The 20 vertices of a dodecahedron lie on 4 parallel planes. 10 form two pentagonal faces of the dodecahedron. The 10 remaining ones will lie on two more parallel planes, forming two larger pentagons. These give 2 of the 12 yellow pentagonal faces hiding in the picture above. We get the rest by slicing the dodecahedron with parallel places in other ways: there are 6 ways, for a total of \(6 \times 2 = 12 \) yellow pentagonal faces.
This shape is an example of a uniform star polyhedron. A 'uniform polyhedron' has regular polygons as faces, with enough symmetries that every vertex looks like every other. In a 'uniform star polyhedron' we also allow regular stars as faces.
I like how uniform star polyhedra look, but I've never been sure the math of them is deep enough to be worth studying. That may sound snobbish. But you see, a lot of uniform polyhedra come from Coxeter groups. These are discrete symmetry groups that are closely connected to lots of other great math - so these are very interesting. The uniform star polyhedra, on the other hand, don't seem connected to other math in such a strong way. Or maybe I just haven't learned how.
Still, they're pretty. There are 57 of them — not counting an infinite number of prisms and antiprisms, star prisms and star antiprisms. You can see them all here:
Puzzle 1. Why does it say "57 varieties" on a bottle of Heinz ketchup? Is it really because there are 57 uniform star polyhedra?
Puzzle 2. What's the most important appearance of the number 57 in group theory?
Puzzle 3. Why is this shape called ditrigonal'?
This picture was made by Tom Ruen using Robert Webb's Stella software and put on Wikimedia Commons. Webb demands a link to his website. For answers to the puzzles, read the comments on my G+ post.
As recently as 6500 BC, Great Britain was connected to Europe! And if you go back further in your time machine, you'll see a huge plain called Doggerland between Britain and Denmark.
Why? Because the sea level is lower during ice ages. More water is locked up in ice!
The last ice age, the Wisconsin glaciation, reached its peak a bit before 18000 BC. Back then, there were huge ice sheets going down to the Great Lakes and the mouth of the Rhine. The north of Britain was covered with ice, and the south was a polar desert!
The light green stuff in this map shows the land a bit later, in 16000 BC. Back then Doggerland was a wide undulating plain full of complicated meandering river systems.
As the ice age ended, the sea level rose rather quickly. Doggerland shrank to the medium green stuff in 8000 BC and the dark green stuff in 7000 BC. One of the last parts to survive was the Dogger Bank. You can see it on the map if you look close. It was an island until 5000 BC.
A new theory says that Doggerland was flooded by a huge tsunami around 6200 BC, thanks to a submarine landslide off the coast of Norway! It's called the Storegga Slide. There's geological evidence of sediments washed up onto land then. Maybe an earthquake triggered a catastrophic expansion of methane hydrates underwater.
This tsunami would have devastated a rich hunting and fishing ground populated by Mesolithic humans. People of some sort have lived on the British Isles, on and off, for much longer! There are flint tools dating back to 815,000 BC. These would not be made by Homo sapiens, since our species only came into existence around 250,000 BC.
But there were Homo sapiens in Britain by 40,000 BC, in the middle of the last ice age. And when that ice age ended and treeless tundra slowly turned into forests of birch trees, more of us moved in. Instead of eating reindeer and wild horses, the ancient Britons started eating pigs, elk, deer, wild boar and wild cattle — hunting them with ever more sophisticated stone tools. So by 6200 BC, when the tsunami crashed over Doggerland, there would have been lots of people living quite well.
Puzzle 1: Why is this area called 'Doggerland'?
Puzzle 2: What's a 'dogger'?
Puzzle 3: When did people start building things around the cite now called Stonehenge — how does that fit into the chronology here?
For answers to the puzzles, read the comments on my G+ post.

This is Alberto Behar in Greenland with the robotic boat he designed. How fast is Greenland melting due to global warming? Where does the water go? Some people sit around and argue. Others go and find out.
It was very warm in Greenland from July 11th to 13th, 2012. Scientists from NASA traveled by helicopter to study the melting ice. They mapped rivers and streams over 5400 square kilometers of Greenland. They found 523 separate drainage systems — small streams joining to form larger streams and rivers.
The water in every one of these flowed into a moulin! A moulin is a circular, vertical shaft. Water pours down the moulin and goes deep below the surface — sometimes forming a layer between ice and the underlying rock. This layer can help glaciers slide down toward the ocean. And this water reaches the ocean fast.
In the area they studied, a total of between 0.13 and 0.15 cubic kilometers of water were flowing into moulins each day. That's a lot! That would be enough to drain 2.5 centimeters of water off the surface each day.
To study the flow of water, Alberto Behar designed two kinds of remote-controlled boats. The boat shown here, was a drone that measured the depth of the water and how much light it reflected, allowing the researchers to calibrate the depth of the surface water from satellite images. They used this boat on lakes and slow-flowing rivers. But for dangerous, swift-flowing rivers, Behar developed disposable robotic drifters that measured the water's velocity, depth and temperature as they swept downstream.
Just a few days ago, Alberto Behar died in a plane crash. The plane he was flying crashed shortly after he took off from a small airport near NASA’s Jet Propulsion Laboratory in Pasadena, California.
So, his coauthors dedicated their paper on this research to him. Here is is:
Check out the cool images and maps. And watch this great movie:

This is not a tornado or hurricane! It's a supercell: a thunderstorm with a deep, persistently rotating updraft.
Supercells are one of the least common kinds of thunderstorm — but they can be the most severe! Supercells can happen anywhere — but especially in the Great Plains of America and the Tornado Corridor of Argentina, Uruguay and southern Brazil.
They start when the wind is moving faster at one height than another: this is called wind shear, and it can create a vortex. Thunderstorms often have a strong updraft, and this can tilt the vortex so it's vertical instead of horizontal! This creates a mesocyclone, which you see here. And sometimes the mesocyclone creates tornadoes.
Things always get more complicated and interesting when you study them in detail. I find weather to be a very tricky subject. I've just skimmed the surface; you can learn more at the links.
This animated gif seems to be created from photos taken in Nebraska by the storm chaser Mike Hollingshead. Google Image Search shows copis of this all over the place, with many people wrongly saying it's a hurricane.
I went through a supercell in an airplane once, shortly after taking off from Denver. We got caught in a downdraft and the pilot had to use full power to get us up and out. Then we turned around and landed back in Denver. It was pretty scary. It made me queasy about flying for a while: not in a rational way, just adrenaline rushes whenever the plane did something funny.
The feeling when you're in a plane dropping through the air reminds me a bit of being in an earthquake as it gets stronger and stronger — you're frozen, wondering: what next? I remember waking up and looking out the window at a street sign wiggling back and forth when the Northridge quake hit in 1994. It wasn't very strong in Riverside, but strong enough that every aftershock made me tense.

On March 7, 1965, protesters seeking the right to vote tried to march from Selma to Montgomery Alabama. State troopers and a violent posse attacked the unarmed marchers with billy clubs and tear gas.
After another try, the march finally succeeded three weeks later. After walking 54 miles, Martin Luther King gave a speech on the steps of the State Capitol of Alabama. It began like this:
Last Sunday, more than eight thousand of us started on a mighty walk from Selma, Alabama. We have walked through desolate valleys and across the trying hills. We have walked on meandering highways and rested our bodies on rocky byways. Some of our faces are burned from the outpourings of the sweltering sun. Some have literally slept in the mud. We have been drenched by the rains. Our bodies are tired and our feet are somewhat sore.But today as I stand before you and think back over that great march, I can say, as Sister Pollard said—a seventy-year-old Negro woman who lived in this community during the bus boycott—and one day, she was asked while walking if she didn't want to ride. And when she answered, "No," the person said, "Well, aren't you tired?" And with her ungrammatical profundity, she said, "My feets is tired, but my soul is rested." And in a real sense this afternoon, we can say that our feet are tired, but our souls are rested.
They told us we wouldn't get here. And there were those who said that we would get here only over their dead bodies, but all the world today knows that we are here and we are standing before the forces of power in the state of Alabama saying, "We ain't goin' let nobody turn us around."
Now it is not an accident that one of the great marches of American history should terminate in Montgomery, Alabama. Just ten years ago, in this very city, a new philosophy was born of the Negro struggle. Montgomery was the first city in the South in which the entire Negro community united and squarely faced its age-old oppressors. Out of this struggle, more than bus desegregation was won; a new idea, more powerful than guns or clubs was born. Negroes took it and carried it across the South in epic battles that electrified the nation and the world.
Yet, strangely, the climactic conflicts always were fought and won on Alabama soil. After Montgomery.s, heroic confrontations loomed up in Mississippi, Arkansas, Georgia, and elsewhere. But not until the colossus of segregation was challenged in Birmingham did the conscience of America begin to bleed. White America was profoundly aroused by Birmingham because it witnessed the whole community of Negroes facing terror and brutality with majestic scorn and heroic courage. And from the wells of this democratic spirit, the nation finally forced Congress to write legislation in the hope that it would eradicate the stain of Birmingham. The Civil Rights Act of 1964 gave Negroes some part of their rightful dignity, but without the vote it was dignity without strength.
Once more the method of nonviolent resistance was unsheathed from its scabbard, and once again an entire community was mobilized to confront the adversary. And again the brutality of a dying order shrieks across the land. Yet, Selma, Alabama, became a shining moment in the conscience of man. If the worst in American life lurked in its dark streets, the best of American instincts arose passionately from across the nation to overcome it. There never was a moment in American history more honorable and more inspiring than the pilgrimage of clergymen and laymen of every race and faith pouring into Selma to face danger at the side of its embattled Negroes.
The confrontation of good and evil compressed in the tiny community of Selma generated the massive power to turn the whole nation to a new course. A president born in the South had the sensitivity to feel the will of the country, and in an address that will live in history as one of the most passionate pleas for human rights ever made by a president of our nation, he pledged the might of the federal government to cast off the centuries-old blight. President Johnson rightly praised the courage of the Negro for awakening the conscience of the nation.
On our part we must pay our profound respects to the white Americans who cherish their democratic traditions over the ugly customs and privileges of generations and come forth boldly to join hands with us. From Montgomery to Birmingham, from Birmingham to Selma, from Selma back to Montgomery, a trail wound in a circle long and often bloody, yet it has become a highway up from darkness. Alabama has tried to nurture and defend evil, but evil is choking to death in the dusty roads and streets of this state. So I stand before you this afternoon with the conviction that segregation is on its deathbed in Alabama, and the only thing uncertain about it is how costly the segregationists and Wallace will make the funeral.
The whole speech is here:
The arc of the moral universe is long, but it bends toward justice.
I used to wonder if this is true. I now think it's one of those things that only becomes true if enough of us work to make it so. A master orator, Martin Luther King was not trying to describe the world: he was trying to change it.
I saw the movie Selma, and I recommend it—a good reminder of this recent era of American history... and how powerful determination accomplished real changes. We could use some of that spirit now.

Mars is a windy place! This dust devil, roughly 20 kilometers high but just 70 meters wide, was seen whirling through northern Mars on March 14, 2007. It was imaged by a high resolution camera on the Mars Reconnaissance Orbiter... and NASA made this animation based on what they saw.
Dust devils happen on Earth too — I often see them in the deserts around here! They're spinning columns of air, made visible by the dust they pull off the ground. Unlike tornadoes, they usually form on clear days when the ground is heated by the sun, warming the air just above the ground.
As hot air rises, it can start to rotate, by chance... and as more hot air rushes in to replace the air that is rising, the rotation becomes stronger. So the dust devil grows and sustains itself, becoming a quick way for hot air to rise... until it dies.
Puzzle: why does it die?
In short, a dust devil is a great example of how efficient increase in entropy can actually create ordered structures, which however have a finite lifetime. You are an example of this.
Maybe this is why many cultures have considered dust devils to be sentient beings. In Arabia they're djinn, or genies. Among the Navajo they're chindii, or spirits of the dead.
This dust devil happened in Amazonis Planitia during the late spring, two weeks short of the northern summer solstice, when the ground in the northern mid-latitudes is heated most strongly by the sun.
The Mars Reconnaissance Orbiter has been examining the Red Planet with six science instruments since 2006. You can see thousands of images taken by HiRISE — the High Resolution Imaging Science Experiment — at this website:
They're awesome!Mars has a very thin atmosphere, with approach of only 600 pascals, tiny compared to Earth's 101,000 pascals — but there are high winds thanks to the enormous daily temperature variations: the temperature typically swings by 100 Celsius each day! This creates winds that easily gust above 90 kilometers/hour, and huge dust storms that envelope the whole planet. The dramatic heating of air at the ground is the perfect recipe for a huge dust devil.
The physics of wind-blown sand and dust is fascinating and complex:
This paper discusses processes on both Earth and Mars. It also seems that static electricity plays an important role in 'saltation', the process whereby wind-blown sand grains hop along the ground:
Abstract: In a wind-blown sand layer, it has been found that wind transport of particles is always associated with separation of electric charge. This electrification in turn produces some electrostatic forces in addition to the gravitational and fluid friction forces that affect the movement of saltating sand particles, further, the wind-blown sand saltation. To evaluate this effect quantitatively, this paper presents a simulation of evolution of wind-blown sand grains after the electrostatic forces exerted on the grains are taken into account in the wind feedback mechanism of wind-blown saltation. That is, the coupling interaction between the wind flow and the saltating sand particles is employed in the simulation to the non-stationary wind and sand flows when considering fluid drag, gravitation, and a kind of electrostatic force generated from a distribution of electric field changing with time in the evolution process of the sand saltation. On the basis of the proposed simulation model, a numerical program is given to perform the simulation of this dynamic process and some characteristic quantities, e.g., duration of the system to reach the steady state, and curves of the saltating grain number, grain transport rate, mass-flux profile, and wind profile varying with time during the non-stationary evolution are displayed. The obtained numerical results exhibit that the electrostatic force is closely related to the average charge-to-mass ratio of sand particles and has obvious influence on these characteristic quantities. The obtained results also show that the duration of the system to reach the steady state, the sand transport rate and the mass flux profile coincide well with experimental results by Shao and Raupach (1992) when the average charge-to-mass ratio of sand particles is 60 microC/kg for the sand particles with average diameter of 0.25 mm. When the average charge-to-mass ratios of sand particles are taken as some other certain values, the calculation results still show that the mass flux profiles are well in agreement with the experimental data by Rasmussen and Mikkelsen (1998) for another category of sand particles, which tell us that the electrostatic force is one of main factors that have to be considered in the research of mechanism of wind-blown sand saltation..
Here's another dust devil on Mars, filmed by the rover Spirit in Gusev Crater:
According to the Mars ocean hypothesis, this is what Mars might have looked like 3.8 billion years ago.
The northern polar plains of Mars, called Vastitas Borealis, are smooth, free of craters, and 4.5 kilometers below the average elevation of the planet. Along the edges there are riverbeds and deltas!
But if there was an ocean, where did the water go?
The gravity on Mars is low, so some could have escaped into space. There's 1.6 cubic kilometers of water ice in the north polar cap, and about the same amount in the south polar cap and its surrounding ice fields. (The south is very different than the north.)
That's not really much water for a whole planet: taken together, just a bit more than the ice on Greenland. But there could be more water ice underground in Vastitas Borealis. Research with MARSIS, a radar instrument on board the Mars Express satellite in orbit around Mars, supports the idea of a large, northern ocean. The instrument revealed that this area has a dielectric constant similar to that of low-density sedimentary deposits, massive deposits of ground ice, or a combination of the two.
But how could Mars have been warm enough for an ocean? Its atmosphere may have been as dense as our Earth's atmosphere is now - and mostly made of carbon dioxide. (Right now it has a carbon dioxide atmosphere just 0.6% as dense as Earth's atmosphere!) That would give a massive greenhouse effect, enough to keep water liquid. In any event, we know there was liquid water, thanks to those riverbeds and deltas.
But the Mars ocean hypothesis is still controversial. For example, Vastitas Borealis has a bunch of boulders on it which are hard to explain if it was an ocean bed. Maybe they were dropped there by icebergs? That happens here on Earth!
The above picture, from Wikicommons, was made by a user named 'lttiz' using data from the Mars Orbiter Laser Altimeter. The elevations were updated so the shore lines will closely approximate their ancient locations, and any mountains less than two billion years old were removed. lttiz also has some other pretty pictures there.
If Mars had an ocean, it would have existed during the
This is Mars as it might have appeared much more recently,
during the height of its last ice age!
Of all planets in the Solar System, Mars has the climate most like
ours. Both Mars and Earth are sensitive to small changes in the shape
of its orbit and the tilt of its axis.
On Earth, when the axis tilts more, the poles warm up and ice ages
end. But a 2003 paper in Nature did simulations and found that Mars
works the other way! When its axis tilts more, the poles warm up, and
the polar ice caps start to evaporate... bringing more water to the
whole planet. But since Mars is below freezing most of the time, that
brings ice all the way down to 300 latitude in both hemispheres, as
shown here.
From about 2.1 million to 400,000 years ago, the increased tilt of
Mars' axis made its poles warmer. But the tilt has been less since
then. This is making the poles colder, so water vapor has been
leaving the zone between 300 and 600 latitude, and collecting in the
ice caps.
If you haven't read Kim Stanley Robinson's trilogy Red Mars,
Green Mars, Blue Mars, you really should. It's a
sprawling tale of the terraforming of Mars, packed with fascinating
digressions. Now I want White Mars.
The photo is from here:
It was prepared for the December 18, 2003, cover of the journal
Nature. The simulated surface deposit is superposed on a map
based on altitude measurements by Global Surveyor and images from
NASA's Viking orbiters of the 1970s.
The paper is here:
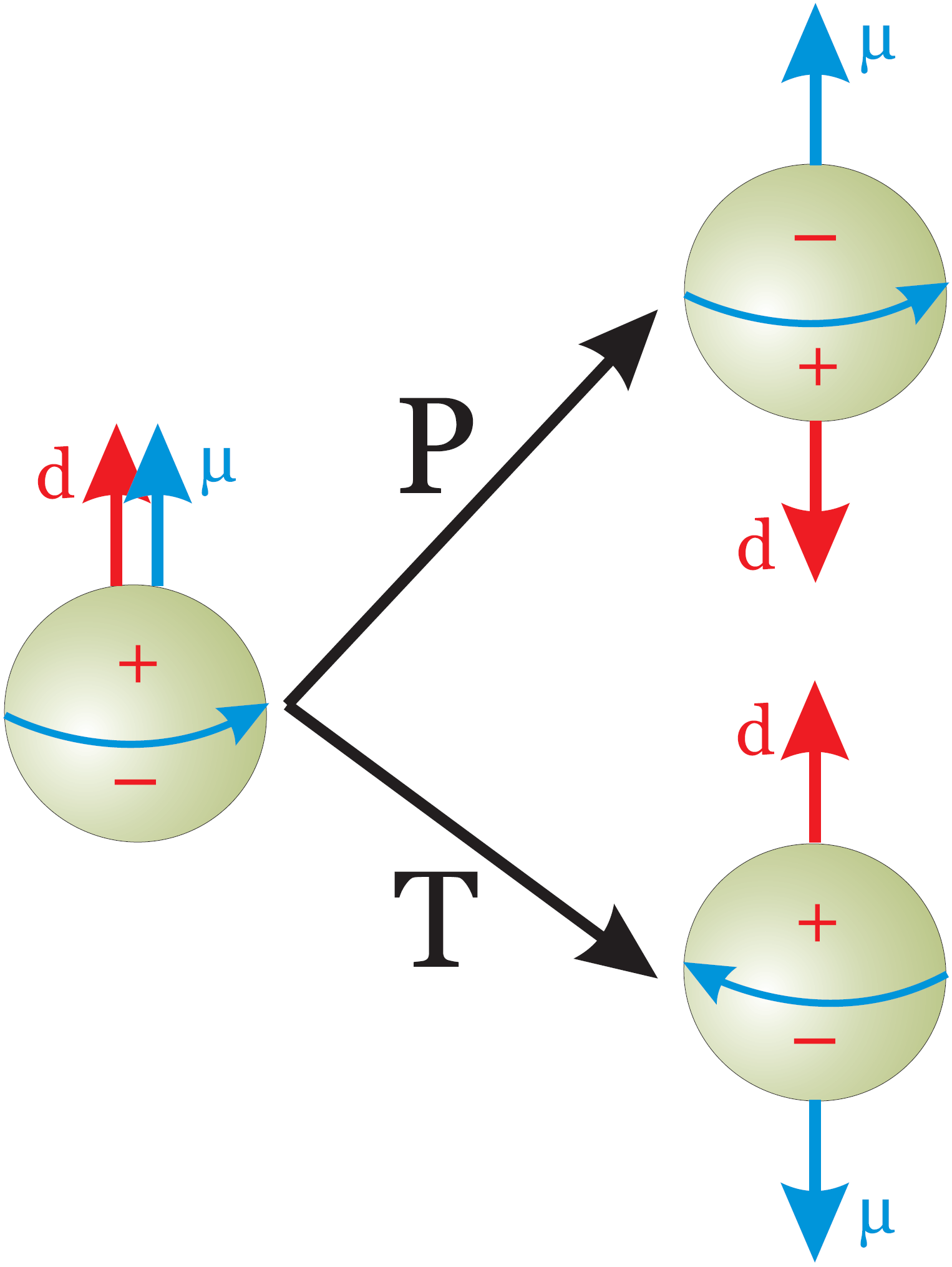
A neutron is a spinning bag of charged particles, so we shouldn't be
surprised that it acts like a little magnet. We say it has a
magnetic dipole moment. This means that like the Earth, it has
a north magnetic pole and a south pole. The blue arrow called \(\mu\)
here points to the north pole.
A neutron might also have an electric dipole moment. That would
happen if there were more positive charge near one pole, and more
negative charge near the other pole. Then we could draw a red arrow
called \(d\) pointing toward the positive charges.
In the picture at left, the red arrow points the same way as the blue
arrow. But nobody knows if there is a red arrow! So far nobody has
seen an electric dipole moment for a neutron. It's either zero, or
very small.
A water molecule has an electric dipole moment: it's shaped like a
head with two big ears, and there's more positive charge near the
ears. You might argue that the electric dipole moment of the neutron
should be zero because — unlike the water molecule — the neutron is
round. There's a kernel of truth to that.
Indeed, if the electric dipole moment wasn't zero, it would violate
some symmetries that the neutron seems to have!
P symmetry, or parity, is the symmetry where you reverse all 3 spatial
directions: send each point \((x,y,z)\) to the opposite point \((-x,-y,-z)\).
If you do this to a spinning sphere, it still spins the same way, so
the arrow \(\mu\) is unchanged. However, if there had been more positive
charges near one pole, now there will be more positive charges near
the other pole. So the arrow \(d\) now points the other way.
T symmetry, or time reversal, is the symmetry where you reverse the
direction of time: send each time \(t\) to \(-t\). We can't actually turn
time around, but we can try to set up a neutron that's a time-reversed
version of some other neutron. It would spin the opposite way, so the
arrow . would point the other way. But the positive charges would
still be on the same side. So \(d\) points the same way.
The picture shows that if a neutron has the \(\mu\) and \(d\) arrows pointing
the same way, and we apply parity or time reversal, we get another
kind of neutron where the \(\mu\) and \(d\) arrows point opposite ways. There
can't be two kinds of neutrons: we'd have noticed that by now. So, if
neutrons have an electric dipole moment, they can't be symmetric under
parity and time reversal.
In fact neutrons probably aren't symmetric under parity and time
reversal, because a force called the weak force doesn't have these
symmetries, and it affects neutrons. But as the name indicates, this
force is very weak. We can calculate the electric dipole moment this
force creates in the neutron, and it's tiny — about 10 million times
smaller than our current ability to measure it.
What's interesting is that as far as we know, the strong force could
also fail to have parity and time reversal symmetry. This is the
force that holds the neutron together. If it broke these symmetries,
it could create a larger electric dipole moment than the weak force
does.
We haven't seen any sign that this happens. People are looking
because this would be one of the best ways to see if the strong force
violates parity and time reversal symmetry. If it doesn't, one of the
fundamental constants of nature must be zero... and nobody knows why,
though there are some fascinating theories. This is called the 'strong
CP problem':
There's a lot more to say about this, but not today!
Puzzle: I said we would have noticed by now if there are two
kinds of neutrons, one where \(\mu\) and \(d\) point the same way and one
where they point in opposite directions. How could we have noticed
this, given that we can't yet measure the \(d\) arrow?
Right now the best upper bound on the neutron's electric dipole moment
is 2.9 · 10-26 e cm. (Electric dipole moment is often
measured in units of the electron's charge times a centimeter.) There
are at least five experiments in progress that aim at improving this
limit to 10-28 e cm. These should be able to rule out various
theories of how supersymmetry could create an electric dipole moment
in the neutron.
The weak force should create a dipole moment of about
10-33 e cm, so detecting that is still far away. This
amount of asymmetry is so small that it's like the Earth being
perfectly round except for mountains that are micron tall!
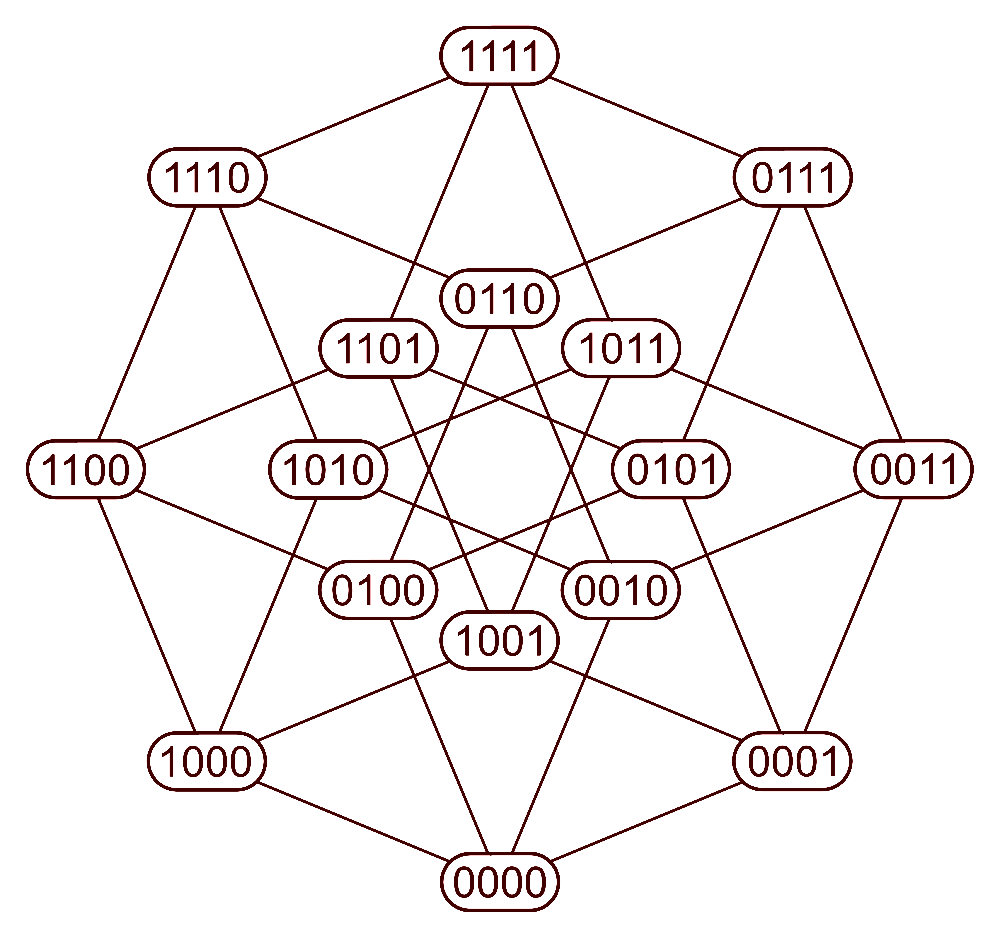
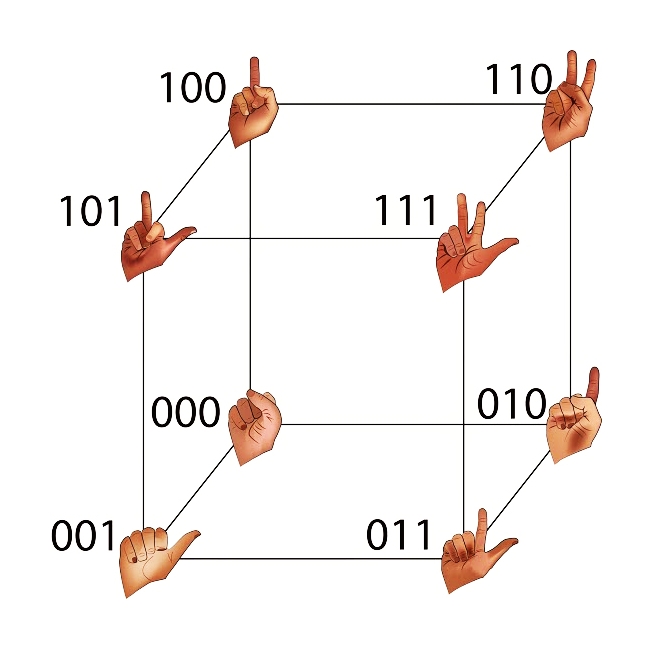
I posted some puzzles about this hypercube of bits, and Scott
Carter responded with a profane version in 3 dimensions:
We can thank photographer Andrey Grachev for this view! He walked
across Lake Baikal, a huge lake in Siberia that freezes over in
winter... and found this ice cave on Olkhon Island.
You can see more of his photos here:
For almost five months a year, Lake Baikal is covered with ice.
Perhaps because it's so deep, it starts freezing only in January, long
after the Siberian frosts become intense. It usually thaws in May.
At its peak, the ice is between 1 and 2 meters thick. Big cracks can
be 10 to 30 kilometers long!
For more on Lake Baikal, including some amazing pictures,
see my October 1st,
2013 diary entry.
If the Greenland ice sheet completely melts, the sea will rise 7.2
meters. This will drown most of the world's coastal cities —
unless we move them or build dikes. So ice on Greenland is important.
It's also a fascinating record of the past! Scientists just made this
wonderful cross-section of Greenland, showing 4 kinds of ice:
This cross-section is just part of a detailed 3d map of Greenland, built using ice core samples and radar from planes. Here's a great video that shows the whole 3d map and how it was made:
The Greenland ice sheet is melting at a rate of about 200 cubic
kilometers per year. The rate is increasing at about 1718 cubic
kilometers per year each year. This sounds bad. Indeed, Greenland is
contributing about as much to sea level rise as Antarctica. But the
Greenland ice sheet won't go away soon. It has about 2,850,000 cubic
kilometers of ice!
Ice from the last interglacial — the Eemian — was only
recently found in Greenland. For more, read this story by Eric Steig:
Puzzle 2: about how many gigatonnes of water are in a cubic kilometer?
Puzzle 3: if it were spread equally over the whole ocean, how
much would a cubic kilometer of water raise the sea level?
You can see some answers on my G+ post.

Puzzle 1: if you extrapolate the constantly accelerating rate
of melting that I described, when would the Greenland ice sheet be
completely melted? Of course this is naive, but the calculation is
easy and fun.
For my February 2015 diary, go here.