3.4
The octonions are fascinating in themselves, but the magic really starts
when we use them to construct the exceptional Jordan algebra ![]() and its associated projective space, the octonionic projective plane.
The symmetry groups of these structures turn out to be exceptional Lie
groups, and triality gains an eerie pervasive influence over the
proceedings, since an element of
and its associated projective space, the octonionic projective plane.
The symmetry groups of these structures turn out to be exceptional Lie
groups, and triality gains an eerie pervasive influence over the
proceedings, since an element of ![]() consists of 3 octonions and
3 real numbers. Using the relation between normed division algebras and
trialities, we get an isomorphism
consists of 3 octonions and
3 real numbers. Using the relation between normed division algebras and
trialities, we get an isomorphism
However, this picture of ![]() in terms of 8-dimensional Euclidean
geometry is just part of a bigger picture — a picture set in
10-dimensional Minkowski spacetime! If we regard
in terms of 8-dimensional Euclidean
geometry is just part of a bigger picture — a picture set in
10-dimensional Minkowski spacetime! If we regard ![]() as sitting
in the lower right-hand corner of
as sitting
in the lower right-hand corner of ![]() , we get an isomorphism
, we get an isomorphism
This picture gives a representation of ![]() as linear
transformations of
as linear
transformations of ![]() . Unfortunately, most of these
transformations do not preserve the Jordan product on
. Unfortunately, most of these
transformations do not preserve the Jordan product on ![]() . As we
shall see, they only preserve a lesser structure on
. As we
shall see, they only preserve a lesser structure on ![]() : the determinant. However, the transformations coming from the subgroup
: the determinant. However, the transformations coming from the subgroup
![]() do preserve the Jordan product. We can
see this as follows. As a representation of
do preserve the Jordan product. We can
see this as follows. As a representation of ![]() ,
, ![]() splits into 'space' and 'time':
splits into 'space' and 'time':
This does not exhaust all the symmetries of ![]() , since there are
other automorphisms coming from the permutation group on 3 letters,
which acts on
, since there are
other automorphisms coming from the permutation group on 3 letters,
which acts on
![]() and
and
![]() in
an obvious way. Also, any matrix
in
an obvious way. Also, any matrix ![]() acts by conjugation as
an automorphism of
acts by conjugation as
an automorphism of ![]() ; since the entries of
; since the entries of ![]() are real, there
is no problem with nonassociativity here. The group
are real, there
is no problem with nonassociativity here. The group ![]() is
36-dimensional, but the full automorphism group
is
36-dimensional, but the full automorphism group ![]() is much
bigger: it is 52-dimensional. As we explain in Section 4.2, it
goes by the name of
is much
bigger: it is 52-dimensional. As we explain in Section 4.2, it
goes by the name of ![]() .
.
However, we can already do something interesting with the automorphisms
we have: we can use them to diagonalize any element of ![]() . To
see this, first note that the rotation group, and thus
. To
see this, first note that the rotation group, and thus ![]() , acts
transitively on the unit sphere in
, acts
transitively on the unit sphere in ![]() . This means we can use an
automorphism in our
. This means we can use an
automorphism in our ![]() subgroup to bring any element of
subgroup to bring any element of ![]() to the form
to the form
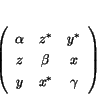
To understand ![]() , we need to understand projections in
, we need to understand projections in ![]() .
Here is where our ability to diagonalize matrices in
.
Here is where our ability to diagonalize matrices in ![]() via
automorphisms comes in handy. Up to automorphism, every projection in
via
automorphisms comes in handy. Up to automorphism, every projection in
![]() looks like one of these four:
looks like one of these four:
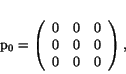
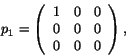
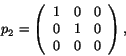
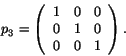
It follows that the points of the octonionic projective plane are
projections with trace 1 in ![]() , while the lines are projections
with trace 2. A calculation [50] shows that any projection
with trace 1 has the form
, while the lines are projections
with trace 2. A calculation [50] shows that any projection
with trace 1 has the form
We use ![]() to stand for the set of points in the octonionic
projective plane. Given any nonzero element
to stand for the set of points in the octonionic
projective plane. Given any nonzero element
![]() with
with
![]() , we can normalize it and then use equation
(3.4) to obtain a point
, we can normalize it and then use equation
(3.4) to obtain a point
![]() . Copying the
strategy that worked for
. Copying the
strategy that worked for ![]() , we can make
, we can make ![]() into a smooth manifold
by covering it with three coordinate charts:
into a smooth manifold
by covering it with three coordinate charts:
We thus obtain the following picture of the octonionic projective plane.
As a manifold, ![]() is 16-dimensional. The lines in
is 16-dimensional. The lines in ![]() are
copies of
are
copies of ![]() , and thus 8-spheres. For any two distinct points in
, and thus 8-spheres. For any two distinct points in
![]() , there is a unique line on which they both lie. For any two
distinct lines, there is a unique point lying on both of them. There is
a 'duality' transformation that maps points to lines and vice versa
while preserving this incidence relation. In particular, since the
space of all points lying on any given line is a copy of
, there is a unique line on which they both lie. For any two
distinct lines, there is a unique point lying on both of them. There is
a 'duality' transformation that maps points to lines and vice versa
while preserving this incidence relation. In particular, since the
space of all points lying on any given line is a copy of ![]() , so
is the space of all lines containing a given point!
, so
is the space of all lines containing a given point!
To dig more deeply into the geometry of ![]() one needs another
important structure on the exceptional Jordan algebra: the determinant.
We saw in Section 3.3 that despite noncommutativity and
nonassociativity, the determinant of a matrix in
one needs another
important structure on the exceptional Jordan algebra: the determinant.
We saw in Section 3.3 that despite noncommutativity and
nonassociativity, the determinant of a matrix in ![]() is a
well-defined and useful concept. The same holds for
is a
well-defined and useful concept. The same holds for ![]() ! We
can define the determinant of a matrix in
! We
can define the determinant of a matrix in ![]() by
by
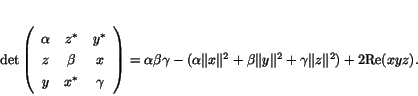
The determinant is a cubic form on ![]() , so there is a unique symmetric
trilinear form
, so there is a unique symmetric
trilinear form
We have already seen that points of ![]() correspond to trace-1
projections in
correspond to trace-1
projections in ![]() . Freudenthal [36] noticed that
these are the same as elements
. Freudenthal [36] noticed that
these are the same as elements
![]() with
with ![]() and
and
![]() . Even better, we can drop the equation
. Even better, we can drop the equation ![]() as
long as we promise to work with equivalence classes of nonzero
elements satisfying
as
long as we promise to work with equivalence classes of nonzero
elements satisfying
![]() , where two such elements are
equivalent when one is a nonzero real multiple of the other. Each
such equivalence class
, where two such elements are
equivalent when one is a nonzero real multiple of the other. Each
such equivalence class ![]() corresponds to a unique point of
corresponds to a unique point of ![]() ,
and we get all the points this way.
,
and we get all the points this way.
Given two points ![]() and
and ![]() , their cross product
, their cross product ![]() is
well-defined up to a nonzero real multiple. This suggests that we define
a 'line' to be an equivalence class of elements
is
well-defined up to a nonzero real multiple. This suggests that we define
a 'line' to be an equivalence class of elements
![]() , where again two such elements are deemed equivalent if one
is a nonzero real multiple of the other. Freudenthal showed that we
get a projective plane isomorphic to
, where again two such elements are deemed equivalent if one
is a nonzero real multiple of the other. Freudenthal showed that we
get a projective plane isomorphic to ![]() if we take these as our
definitions of points and lines and decree that the point
if we take these as our
definitions of points and lines and decree that the point ![]() lies on
the line
lies on
the line ![]() if and only if
if and only if ![]() . Note that this equation
makes sense even though
. Note that this equation
makes sense even though ![]() and
and ![]() are only well-defined up to
nonzero real multiples.
are only well-defined up to
nonzero real multiples.
One consequence of all this is that one can recover the structure of
![]() as a projective plane starting from just the determinant on
as a projective plane starting from just the determinant on
![]() : we did not need the Jordan algebra structure! However, to
get a 'duality' map switching points and lines while preserving the
incidence relation, we need a bit more: we need the nondegenerate
pairing
: we did not need the Jordan algebra structure! However, to
get a 'duality' map switching points and lines while preserving the
incidence relation, we need a bit more: we need the nondegenerate
pairing
We thus obtain a very pretty setup for working with ![]() . If we
use the isomorphism between
. If we
use the isomorphism between ![]() and its dual to reinterpret
the cross product as a map
and its dual to reinterpret
the cross product as a map
For more on octonionic geometry, the reader is urged to consult the
original papers of Freudenthal
[35,36,37,38], as well as
those of Jacques Tits [87,88] and Tonny Springer
[80,81,82]. Unfortunately, we must now bid
goodbye to this subject and begin our trip through the exceptional
groups. However, we shall return to study the symmetries of ![]() and
the exceptional Jordan algebra in Sections 4.2 and 4.4.
and
the exceptional Jordan algebra in Sections 4.2 and 4.4.
© 2001 John Baez