To specify a quantum field theory on 3+1-dimensional Minkowski spacetime, we first need to list the elementary particles. These are irreducible representations (or irreps) of the group
where ISpin(3,1) is the universal cover of the identity component of the Poincaré group, while G is some compact Lie group called the internal symmetry group. Then we need to list the interactions, which are intertwining operators between tensor products of these irreps.
The Standard Model is the currently best accepted theory of elementary particles and their interactions, taking quantum theory and special relativity into account, but not general relativity -- i.e., not gravity. There is a huge amount of experimental evidence for this theory, but its mathematical structure remains complicated and mysterious. Nobody really knows `why' nature likes to work this way! However, the Standard Model displays many tantalizing patterns, which are probably important clues. In the following exercises you will ponder the elementary particles of the Standard Model. We will not discuss the interactions yet.
In the Standard Model, the internal symmetry group is
An irrep of a product of a bunch of groups is the same as a tensor product of irreps of these groups. Thus, to specify an elementary particle in the Standard Model, we just need to specify irreps of ISpin(3,1), SU(3), SU(2) and U(1).
The groups SU(3), SU(2) and U(1) roughly correspond to the three forces other than gravity: strong, weak, and electromagnetic. The strong force holds quarks together in particles like protons and neutrons. The weak force lets one sort of quark or lepton turn into another, which is the process responsible for many radioactive decays in nuclei, and which also occurs in nuclear fusion. The electromagnetic force is the most familiar of the lot.
However, there's a sneaky twist. Specifying an irrep of
SU(3) says how an elementary particle interacts with the
strong force. Specifying an irrep of U(1) says how it
interacts with the electromagnetic force. In
particular, the unitary irreps of
U(1) are labelled by an integer
called electric charge: for each integer Q
there is an irrep
of U(1) on
![]() in which any element α of U(1) acts on a
vector x in
in which any element α of U(1) acts on a
vector x in
![]() to give αQx, and we say this irrep
describes an elementary particle of charge
Q. But,
the
U(1) group describing electromagnetism is not the obvious
U(1) subgroup of
SU(2) × U(1)!
It's actually some other
U(1) subgroup of
SU(2) × U(1),
which we will describe later.
What this means is that the weak and electromagnetic forces
are described using
SU(2) × U(1) in a
tangled-up, "unified" way. For this reason, physicists say that
specifying an irrep of
SU(2) × U(1)
says how an elementary
particle interacts with the "electroweak force".
to give αQx, and we say this irrep
describes an elementary particle of charge
Q. But,
the
U(1) group describing electromagnetism is not the obvious
U(1) subgroup of
SU(2) × U(1)!
It's actually some other
U(1) subgroup of
SU(2) × U(1),
which we will describe later.
What this means is that the weak and electromagnetic forces
are described using
SU(2) × U(1) in a
tangled-up, "unified" way. For this reason, physicists say that
specifying an irrep of
SU(2) × U(1)
says how an elementary
particle interacts with the "electroweak force".
It would take quite a while to explain this better, and it's impossible
without describing the interactions. For now, let's just see
which irreps of
correspond to elementary particles in the Standard Model.
Again, to get an irrep of this group, we just need to take irreps of ISpin(3,1), SU(3), SU(2), and U(1) and tensor them all together. The following chart lists what these irreps are for every particle in the Standard Model:
| type of particle | ISpin(3,1) irrep | SU(3) irrep | SU(2) irrep | U(1) irrep |
| GAUGE BOSONS | ||||
|
|
massless spin-1 | |||
| massless spin-1 | ||||
| massless spin-1 | ||||
| HIGGS BOSON | ||||
| massless spin-0 | ||||
| and its antiparticle! | ||||
| FIRST GENERATION FERMIONS | ||||
| Leptons: | ||||
| left-handed massless spin-1/2 | ||||
| right-handed massless spin-1/2 | ||||
| right-handed massless spin-1/2 | ||||
| and their antiparticles! | ||||
| Quarks: | ||||
|
|
left-handed massless spin-1/2 | |||
|
|
right-handed massless spin-1/2 |
|
||
|
|
right-handed massless spin-1/2 |
|
||
| and their antiparticles! | ||||
| SECOND GENERATION FERMIONS | ||||
| Leptons: | ||||
|
|
left-handed massless spin-1/2 | |||
| right-handed massless spin-1/2 | ||||
| right-handed massless spin-1/2 | ||||
| and their antiparticles! | ||||
| Quarks: | ||||
|
|
left-handed massless spin-1/2 | |||
|
|
right-handed massless spin-1/2 |
|
||
|
|
right-handed massless spin-1/2 |
|
||
| and their antiparticles! | ||||
| THIRD GENERATION FERMIONS | ||||
| Leptons: | ||||
|
|
left-handed massless spin-1/2 | |||
| right-handed massless spin-1/2 | ||||
| right-handed massless spin-1/2 | ||||
| and their antiparticles! | ||||
| Quarks: | ||||
|
|
left-handed massless spin-1/2 | |||
|
|
right-handed massless spin-1/2 |
|
||
|
|
right-handed massless spin-1/2 |
|
||
| and their antiparticles! |
Here are some conventions used in the above chart:
Similarly, we use "red", "blue" and "green"
-- or
We sometimes combine the two previous conventions.
For example, the left-handed up and down quarks correspond to
the representation
The reason for using multiples of
For any complex vector space
In physics, conjugate representations describe antiparticles.
In the above chart, wherever we write "and its antiparticle",
we mean that
in addition to the particle corresponding to the representation shown,
there is also a particle corresponding to the complex conjugate of
this representation.
Now for some problems:
1. List the nine most interesting patterns you can find
in the above chart -- not counting the patterns mentioned
in the following exercises.
2. Ignoring
ISpin(3,1) for a moment, all the fermions of the
first generation correspond to complex irreps of
Let's call the direct sum of
all these irreps the first-generation fermion representation
of G, or
What is the dimension of
3.
What particle corresponds to this trivial representation? This
particle don't interact at all with the strong, weak or
electromagnetic forces, so it's very hard to see. Physicists have
only become convinced of its existence in the last couple of years.
Before this, they used a different version of the Standard Model,
where instead of
4. If we define second-generation
and third-generation fermion representations
as we did for the first generation, what are these representations
like? The direct sum of all three of these representations could
be called the fermion representation of G.
What is the dimension of this representation?
5. Again ignoring
ISpin (3,1), all the gauge bosons correspond to
real irreps of G.
Let's call the direct sum of all these irreps the
gauge boson representation of G,
or G for short. What would
mathematicians call this representation? What is the dimension of
this representation?
6. Again ignoring ISpin(3,1),
the Higgs boson
corresponds to a complex irrep of
G = SU(3) × SU(2) × U(1).
Let's call this irrep
the Higgs representation of G,
or H for short.
What is the dimension of this representation?
7. Can you think of any interesting patterns involving
Hints: G is a real vector space, while
F and H
are complex vector spaces. Thinking about the dimensions of
F, G and H
may be helpful, especially if you're into numerology.
You can think of them all as real vector spaces, but
then the dimensions of F and H double.
You might want to
keep the ISpin(3,1)
irreps in mind when trying to combine
F, G and H
into something interesting. You may or may not
want to bring all three generations into the picture. Finally, don't
forget the fact that F and H
come along with their conjugate reps
There are some fairly interesting solutions to Problem 7, but I'll be
satisfied with any honest attempt. A really good solution could earn you
a Nobel prize!
© 2003 John Baez
![]() to stand for the trivial 1-dimensional
complex representation of SU(3) or SU(2).
We use
to stand for the trivial 1-dimensional
complex representation of SU(3) or SU(2).
We use
![]() to stand for the trivial 1-dimensional real representation
of SU(3), SU(2) or U(1).
to stand for the trivial 1-dimensional real representation
of SU(3), SU(2) or U(1).
![]() as an abbreviation for the defining
representation of SU(3):
that is, its representation on
as an abbreviation for the defining
representation of SU(3):
that is, its representation on
![]() coming from the fact that SU(3)
consists of 3 × 3
matrices. Similarly, we use
coming from the fact that SU(3)
consists of 3 × 3
matrices. Similarly, we use ![]() as an abbreviation for the
defining representation of SU(2).
as an abbreviation for the
defining representation of SU(2).
![]() . For example,
"left-handed electron neutrino" is just a weird way of
talking about the basis vector
. For example,
"left-handed electron neutrino" is just a weird way of
talking about the basis vector
![]()
while "left-handed electron" is a weird way of talking about
![]()
In old-fashioned physics these are considered different particles,
but in the Standard Model they are really just two basis vectors
for the same irrep of SU(2)!
![]() for
short -- as cute names for a basis
of the defining representation of SU(3) on
for
short -- as cute names for a basis
of the defining representation of SU(3) on
![]() :
:
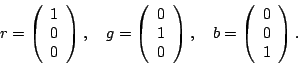
![]() of
SU(3) × SU(2).
This is a 6-dimensional representation with basis
of
SU(3) × SU(2).
This is a 6-dimensional representation with basis
![]()
which physicists abbreviate as
![]()
The conventions get applied in an even more complicated
way for gluons, but you don't need to worry about that now.
![]() , which is called hypercharge and
denoted
, which is called hypercharge and
denoted ![]() . We use
. We use
![]() Y
to stand for the representation of U(1)
on
Y
to stand for the representation of U(1)
on
![]() in which the element
α of U(1) acts on x to give α3Yx.
in which the element
α of U(1) acts on x to give α3Yx.
![]() is purely historical:
quarks were discovered after electrons, and the electric charges of
quarks come out as integer multiples of
is purely historical:
quarks were discovered after electrons, and the electric charges of
quarks come out as integer multiples of ![]() in units where
the electron charge is
in units where
the electron charge is ![]() . Hypercharge is not the same as electric
charge, but they're closely related, so hypercharges wind up being
described as multiples of
. Hypercharge is not the same as electric
charge, but they're closely related, so hypercharges wind up being
described as multiples of ![]() . (The electron, in turn, is
conventionally assigned a negative electric charge because Benjamin
Franklin was mixed up about which way the current flowed in
lightning!)
. (The electron, in turn, is
conventionally assigned a negative electric charge because Benjamin
Franklin was mixed up about which way the current flowed in
lightning!)
![]() ,
, ![]() and
and ![]() as an abbreviation
for the adjoint representations of
SU(3), SU(2), and U(1),
respectively.
as an abbreviation
for the adjoint representations of
SU(3), SU(2), and U(1),
respectively.
![]() there is a conjugate vector
space
there is a conjugate vector
space ![]() , which we get by making
, which we get by making ![]() into a complex vector
space in a different way, such that multiplication by
into a complex vector
space in a different way, such that multiplication by ![]() now acts as
what used to be multiplication by
now acts as
what used to be multiplication by ![]() . Similarly, for any
complex representation of a group on
. Similarly, for any
complex representation of a group on ![]() we get a representation
of this group on
we get a representation
of this group on ![]() , called the conjugate representation.
, called the conjugate representation.
![]() for short.
for short.
![]() ? If you know about Clifford
algebras and spinors, what does this instantly make you wonder? If you were
trying to describe
? If you know about Clifford
algebras and spinors, what does this instantly make you wonder? If you were
trying to describe ![]() using the normed division algebras
using the normed division algebras ![]() and
and ![]() , what might you try?
, what might you try?
![]() contains a one-dimensional trivial representation of G
as a
subrepresentation, so we have
contains a one-dimensional trivial representation of G
as a
subrepresentation, so we have
![]()
where ![]() stands for this trivial representation.
stands for this trivial representation.
![]() they thought the first-generation fermion
representation was
they thought the first-generation fermion
representation was ![]() . What is the dimension of
. What is the dimension of ![]() ? How
would this make you feel if you really liked Clifford algebras
and/or normed division algebras?
? How
would this make you feel if you really liked Clifford algebras
and/or normed division algebras?
![]() , G and
, G and ![]() ? It would be especially
cool if they suggested a way to combine
F
G and H
into some mathematically interesting structure.
? It would be especially
cool if they suggested a way to combine
F
G and H
into some mathematically interesting structure.
![]() and
and ![]() , corresponding to antiparticles.
, corresponding to antiparticles.
![]()
Next: Hypercharge and Weak Isospin
baez@math.removethis.ucr.andthis.eduhome