




|
 
|

|
Today I want to talk about the Enceladus plumes, the Io flux tube, special properties of the number 6 - and the wonders of standard Borel spaces, commutative von Neumann algebras and Polish groups.
Let's start by leaving the fire and brimstone of Io. Let's sail out to the icy splendor of Saturn's moon Enceladus, and gaze at its geysers:

1) NASA Photojournal, Jet blue, http://photojournal.jpl.nasa.gov/catalog/PIA08386
We've seen Enceladus once before, in "week231". I showed you a photo of the icy geysers near its south pole, taken by the Cassini probe back in 2005. Above is a prettier version of the same picture, released this August to celebrate Cassini's return to Enceladus. You can see the geysers shooting plumes of ice into outer space!
You see, this year NASA has been using the Cassini probe to take a better look at large cracks on the icy surface of Enceladus. They're called "tiger stripes", and this where the geysers are. On August 11th, the Cassini probe shot past Enceladus at a distance of just 50 kilometers. It took some wonderful photos as it approached:

2) NASA Photojournal, Great southern land, http://photojournal.jpl.nasa.gov/catalog/PIA11112
Here you see the four main tiger stripes on Enceladus. They're the big greenish cracks near the south pole, running from left to right. For some reason these tiger stripes are named after cities mentioned in that wonderful book of tales called One Thousand and One Nights. From top to bottom: Damascus Sulcus, Baghdad Sulcus, Cairo Sulcus and Alexandria Sulcus. "Sulcus" is Latin for a depression or fissure. It's often used as a medical term, especially for features of the brain - but on Enceladus it just means "tiger stripe".
These tiger stripes are about 2 kilometers wide and 500 meters deep. They're flanked by ridges that are about 2-4 kilometers wide and 100 meters tall. The Damascus and Baghdad Sulci are the most active ones, as far as geysers go:
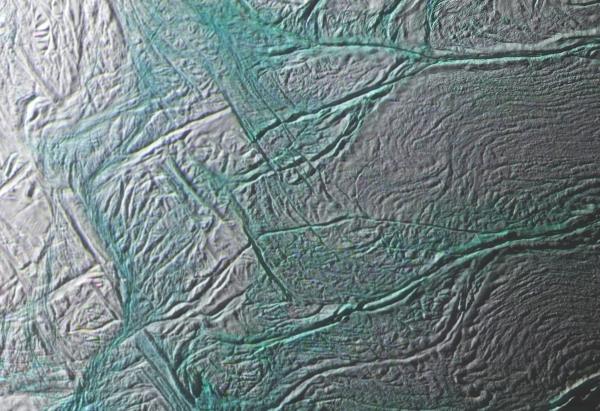
Alexandria Sulcus is the least active.
The white stuff in this false-color image is fine-grained ice. The green stuff is bigger chunks of ice - even house-sized boulders. These bigger chunks are concentrated along valley floors and walls, and along the upraised flanks of the tiger stripes.
At its closest approach, Cassini took much higher resolution photographs of the tiger stripes, like this closeup of the big fork in Damascus Sulcus:
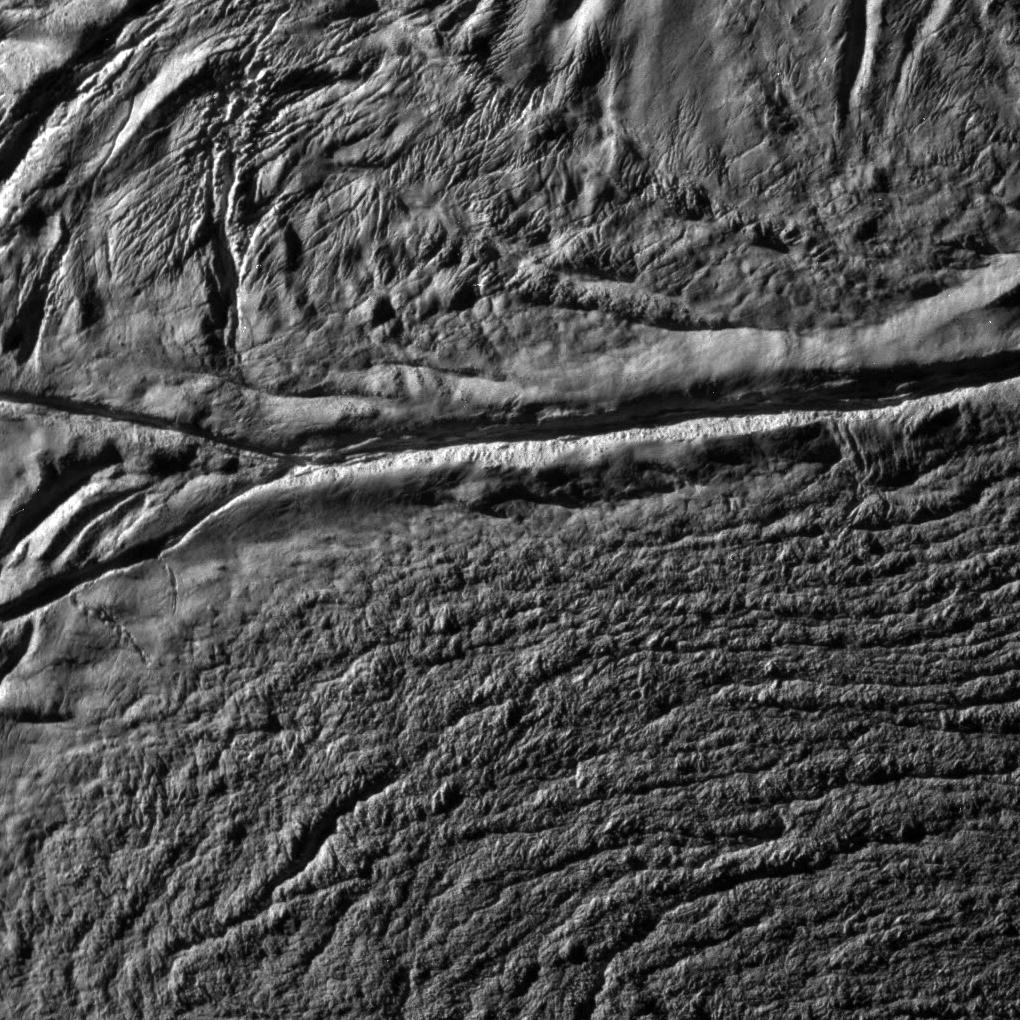
3) NASA Photojournal, Damascus Sulcus on Enceladus, http://photojournal.jpl.nasa.gov/catalog/PIA11113
The hard part was compensating for the fact that the spacecraft was whizzing by the moon. The NASA team used a clever maneuver they called a "skeet shoot" to tackle this problem:
On Earth, skeet shooting is an outdoor shotgun sport that simulates shooting game birds in flight. A small Frisbee-like ceramic disk, called a clay pigeon, is launched through the air, usually diagonally across in front of a shooter armed with a shotgun. The skill in successfully hitting the moving clay target with the birdshot is for the shooter to point a little ahead of the clay pigeon, and match its angular velocity when the trigger is pulled. The clay pigeon then passes into the bird shot at exactly when the shot arrives at its destination in the path of the moving target. So far so good. At and just after closest-approach on the Enceladus 4 flyby, relative to Cassini and Optical Remote Sensing boresight directions, Enceladus was streaking too quickly across the sky for the spacecraft to be able to stably target and track any geological feature on the surface. Borrowing from the firearms sport, the trick was to turn the spacecraft as fast as possible in the same direction as Enceladus' path across the sky. The plan was to be leading Enceladus and match its angular velocity at the exact times when our targets of interest passed into our camera's field of view.It worked amazingly well. They got some photos that could see features as small as 10 meters! It's great fun to read blogs of the scientists involved, and watch a video of the maneuver:
4) NASA Blogs, Enceladus - Aug08, http://blogs.nasa.gov/cm/blog/cassini-aug08/
During this flyby, an infrared spectrometer on the Cassini probe saw that the tiger stripes are significantly warmer than their surroundings. Here's a temperature map with approximate locations of active geysers. From left to right you can see Damascus Sulcus, Baghdad Sulcus, Cairo Sulcus and Alexandria Sulcus:
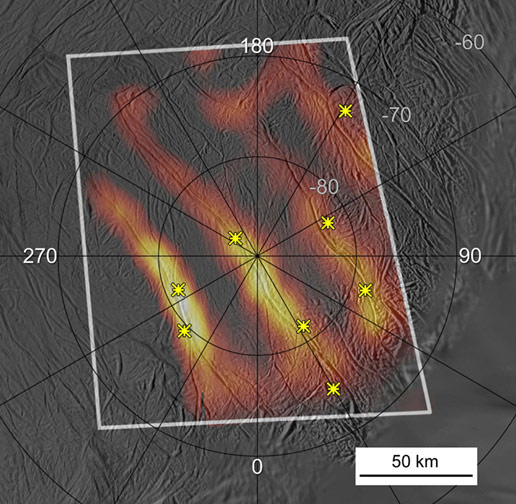
5) NASA Photojournal, Jet spots in tiger stripes, http://photojournal.jpl.nasa.gov/catalog/PIA10361
Other instruments detected a plume of water vapor, ice, methane, carbon dioxide, nitrogen, and more complicated organic compounds. All this is good evidence for "cryovolcanism": a version of volcanic activity that can happen on really cold worlds, with water playing the role of lava. Cryovolcanism has also been seen on other moons of outer planets: Triton, Europa, Titan, Ganymede and Miranda.
Cassini made two more flybys in October, and another in November:
6) NASA Blogs, Enceladus, http://blogs.nasa.gov/cm/blog/enceladus
And just this week, Candice Hansen and her coauthors came out with a new paper about the geysers of Enceladus:
7) C. J. Hansen, L. W. Esposito, A. I. F. Stewart, B. Meinke, B. Wallis, J. E. Colwell, A. R. Hendrix, K. Larsen, W. Pryor and F. Tian, Water vapour jets inside the plume of gas leaving Enceladus, Nature 456 (27 November 2008), 477-479.
8) NASA, Enceladus Jets: Are They Wet or Just Wild?, http://www.nasa.gov/mission_pages/cassini/whycassini/cassinif-20081126.html
They analyzed data from the ultraviolet spectrometer on Cassini and saw four separate jets of water blocking out the light of distant stars. With further clever reasoning they estimated the velocity of these jets. They seem to be moving at supersonic speeds - up to 2000 kilometers per hour.
Then, they argue that such high speeds are only possible if there's lots of underground liquid water near the surface on this part of Enceladus!
This conclusion is still controversial. Susan Kieffer of the University of Illinois at Urbana-Champaign has a competing theory, which says the water is in the form of gas clathrates. I showed you pictures of these back in "week269": they're cage-shaped ice crystal structures that trap gas molecules inside. There are about 6 trillion tons of gas clathrates on the ocean floors here on Earth. Maybe they're also on Enceladus:
9) Susan W. Kieffer, Xinli Lu, Craig M. Bethke, John R. Spencer, Stephen Marshak, Alexandra Navrotsky, A clathrate reservoir hypothesis for Enceladus' south polar plume, Science 314 (15 December 2006), 1764-1766.
Only time will tell.
What's not controversial is that the geysers of Enceladus shoot out plumes of stuff - mainly water vapor and ice, but also other gases and dust - at speeds exceeding escape velocity. Enceladus is small: just 500 kilometers across. So its gravity is weak; its escape velocity is low. So it's easy for geysers to blast stuff straight out into space.
And then what? Then it spreads out and form a huge ring around Saturn: the "E ring". The E ring is much more diffuse than the really famous rings of Saturn. It's much further out, and usually almost invisible. But here's a great photo of the E ring, again taken by the hero of this story - the Cassini probe:

10) NASA Photojournal, Ghostly fingers of Enceladus, http://photojournal.jpl.nasa.gov/catalog/PIA08321
The trick was to take the shot with the sun almost directly behind the camera. Unexpected wispy patterns may hint at interactions between the ring and Saturn's magnetic field. Enceladus is the white blob in the middle of the ring. If you look carefully, you can see its geysers... and you can even see it carving a path through the E ring!
By the way, the volcanic activity on Io also produces a kind of ring: a of ionized sulfur, oxygen, sodium, and chlorine. And since the magnetic field of Jupiter is very strong, and Io is close by, this causes dramatic effects. For example, charged particles from this plasma torus are funnelled down something called the "Io flux tube" to Jupiter's surface, where they create light shows 1000 times brighter than the aurora borealis here on earth! You can see pictures here:
11) Astronomy Picture of the Day, Jovian aurora, http://apod.nasa.gov/apod/ap980123.html
Next: some exceptional properties of the number 6.
Every set has a group of symmetries, but so does every group. The symmetries of a group are called "automorphisms" of the group. Every symmetry of a set gives a symmetry of its group of its symmetries, called an "inner automorphism". But of all finite sets, only the six-element set has a symmetry group with an EXTRA symmetry - a symmetry that doesn't come from a symmetry of that set! This is called an "outer automorphism".
In more jargonesque terms: of all the permutation groups Sn, only S6 has an outer automorphism. It has just one, and I described it here:
12) John Baez, Some thoughts on the number six, http://math.ucr.edu/home/baez/six.html
Recently my friend Bruce Westbury told me some more cool facts about the number 6. One of these is another nice description of the outer automorphism of S6. He heard this from the group theorist Brian Bowditch, who heard it from Chris Penrose (Roger's son). I haven't checked it! I'll just pass it on, as gossip, and let you see if it's true.
It goes like this. Start with the icosahedron, drawn as a graph on the sphere, and identify oposite points. This gives a graph on the projective plane. This graph is called K6: the "complete graph on 6 vertices". In other words, it's the graph with 6 vertices, each one connected to every other one by a single edge. The faces of this graph are triangles. Apparently there are twelve embeddings of K6 in the projective plane and they come in six pairs. Each permutation of the six vertices of K6 induces a permutation of these six pairs. This process gives an automorphism of S6. And apparently this is the outer automorphism!
Westbury later pointed out this related paper:
13) Ben Howard, John Millson, Andrew Snowden, Ravi Vakil, A description of the outer automorphism of S6, and the invariants of six points in projective space, available as arXiv:0710.5916.
I haven't checked to see if the results here imply the claim above.
Another group theorist, Derek Holt, told Westbury about an intriguing conjecture which he believes but has not had the energy to check.
Take a finite simple group and choose two elements at random. What is the probability that they generate the group?
One cool fact is that this probability is never zero. Every finite simple group can be generated by two elements! So, they're all quotients of the free group on two generators.
Another cool fact is that this probability tends to 1 as the order of the group tends to infinity:
14) M. Liebeck and A. Shalev, The probability of generating a finite simple group, Geometrica Dedicata 56 (1995), 103-111.
This implies that this probability attains a mininum value for some finite simple group. For A6 - the group of even permutations of a 6-element set - the probability is 53/90. Holt's conjecture is that this is the minimum among all finite simple groups.
Here are the probabilities for a few finite simple groups, listed in order of increasing size:
A2 1 = 1.000
A3 8/9 ~ .889
PSL(2,3) ≅ A4 2/3 ~ .667
PSL(2,4) ≅ PSL(2,5) ≅ A5 19/30 ~ .633
PSL(2,7) ≅ PSL(3,2) 19/28 ~ .679
PSL(2,8) 71/84 ~ .845
PSL(2,9) ≅ A6 53/90 ~ .589
PSL(2,11) 127/165 ~ .770
A7 229/315 ~ .727
PSL(4,2) ≅ A8 133/180 ~ .739
A9 15403/18144 ~ .849
Here An is the group of even permutations of an n-element set, while PSL(n,q) is the group of n × n matrices with determinant 1 having entries in the field with q elements, mod multiples of the identity matrix. Of the groups listed above, only A4 is not simple. I included this one just because I wanted to list all the unexpected isomorphisms between "alternating" groups (An's) and "projective special linear" groups (PSL's).
(Each of these isomorphisms makes a wonderful story in itself - but not for today! If you want to know these stories, try the first of Conway's "Three Lectures on Exceptional Groups" from his book with Sloane on Sphere Packings, Lattices and Groups. Also try "week79", to see how these stories are related to Galois' fatal duel and the buckyball.)
So, you see the number 6 has several special properties, all related to permutations of a 6-element set. What do these special properties really mean? I don't know! They're just little clues waiting for a big mystery story to come along.
Lately I've been finishing up a big paper on infinite-dimensional representations of 2-groups, which I'm writing along with my former student Derek Wise, the physicist Laurent Freidel, and his student Aristide Baratin. Derek and Aristide are doing all the really hard work, but I used to do functional analysis when I was a youngster, and there's a lot of measure theory in our paper, so sometimes it's my job to dig up papers on this subject and see if they help. And this sort of work can actually be fun, once I get into the mood.
I don't want to try to explain this paper now. I just feel like explaining some tidbits of measure theory that I've picked up while writing it.
A measure space is basically a space that you can do integrals over. But some measure spaces are better than others. Some of them are immensely huge and nasty. But "standard Borel spaces" include all the examples I care about, and they're incredibly nice.
So, what's a standard Borel space?
It's a kind of "measurable space", meaning a space equipped a collection of subsets that's closed under countable intersections, countable unions and complement. Such a collection is called a "sigma-algebra", and we call the sets in here "measurable". A "measure" on a measurable space assigns a number between 0 and +∞ to each measurable set, in such a way that for any countable disjoint union of measurable sets, the measure of their union is the sum of their measures.
A nice way to build a measurable space is to start with a topological space. Then you take its open sets and keep taking countable intersections, countable unions and complements until you get a sigma-algebra. This may take a long time, but if you believe in transfinite induction you're bound to eventually succeed. The sets in this sigma-algebra are called "Borel sets".
A basic result in real analysis is that if you put the usual topology on the real line, and use this to cook up a sigma-algebra as just described, there's a unique measure on the resulting measurable space that assigns to each interval its usual length. This is called "Lebesgue measure".
Some topological spaces are big and nasty. But separable complete metric spaces are not so bad.
We don't care about the metric in this game. So, we use the term "Polish space" for a topological space that's homeomorphic to a complete separable metric space.
And often we don't even care about the topology. So, we use the term "standard Borel space" for a measure space whose measurable sets are the Borel sets for some topology making it into a Polish space.
In short: every complete separable metric space has a Polish space as its underlying topological space, and every Polish space has a standard Borel space as its underlying measurable space.
Now, it's hopeless to classify complete separable metric spaces. It's even hopeless to classify Polish spaces. But it's not hopeless to classify standard Borel spaces! The reason is that metric spaces are like diamonds: you can't bend or stretch them at all without breaking them entirely. But topological spaces are like rubber... and measurable spaces are like dust. So, it's very hard for two metric spaces to be isomorphic, but it's easier for their underlying topological spaces - and even easier for their underlying measurable spaces.
For example, the line and plane are isomorphic, if we use their usual sigma-algebras of Borel sets to make them into measurable spaces! And the plane is isomorphic to Rn for every n, and all these are isomorphic to a separable Hilbert space! As measurable spaces, that is.
In fact, every standard Borel space is isomorphic to one of these:
This amazing result has a nice relative in the world of von Neumann algebras.
Starting from a measure space X, we can form the Hilbert space L2(X). We can also form L∞(X), the space of equivalence classes of bounded measurable complex functions on X, where we identify functions that agree except on a set of measure zero.
L∞(X) is an algebra where we multiply functions pointwise. We can think of it as an algebra of multiplication operators on L2(X). In fact, it forms a "von Neumann algebra" - a kind of algebra that's great for quantum theory. I defined von Neumann algebras back in "week175", so I won't do it again here.
L∞(X) is a very special sort of von Neumann algebra, namely a commutative one. There's a nice theorem: every commutative von Neumann algebra is isomorphic (as an abstract C*-algebra) to one of this form. Even better, every commutative von Neumann algebra of operators on a separable Hilbert space is isomorphic to L∞(X) for one of these choices of X:
If you like keeping your categories straight, it may seem annoying to put a topology on your group when you're trying to do measure theory. But apparently some topology is a good thing... either that, or people haven't found the best framework for this subject.
It's a bit slippery, you see. Not every standard Borel group comes from a Polish group. But the counterexamples seem to be horrid. And more importantly, every measurable homomorphism between Polish groups is automatically continuous! So there must be some way to define Polish groups as standard Borel groups with an extra property - not extra structure.
There are other similar results with the same flavor. For example, suppose we have a Polish group G acting as measurable transformations on a standard Borel space X. Then we can make X into a Polish space so that the action of G on X becomes continuous!
(Of course we also require that the new Borel sets of X are the same as its original measurable sets.)
There are also interesting results saying that Polish spaces and Polish groups "aren't too big". Some of these theorems mention the "Hilbert cube" - that is, a countable product of copies of [0,1], with its product topology. This space sounds big, but thanks to Tychonoff's theorem it's compact! It's also metrizable: that is, its topology comes from a metric. And it's separable: it has a countable dense subset. In fact, a topological space is separable and metrizable iff it's homeomorphic to a subset of the Hilbert cube.
Here's how the Hilbert cube relates to Polish spaces: a topological space is a Polish space iff it's homeomorphic to a countable intersection of open subsets of the Hilbert cube!
And here's how the Hilbert cube relates to Polish groups: a topological group is a Polish group iff it's isomorphic to a subgroup of the group of homeomorphisms of the Hilbert cube!
I'll wrap up with a nice fact about measures on standard Borel spaces. A "probability measure" on a measure space X is one that assigns the number 1 to the whole set X. Then the measure of a measurable subset S of X can be interpreted as the probability of a point being in X. This idea of using measures to study probabilities lies at the foundation of modern probability theory.
But here's a lesser-known fact: the set of probability measures on X, say M(X), is itself a measurable space!
How does this work? First we give M(X) its "weak topology". This is the topology where a bunch of measures μi converge to μ if for every bounded continuous function f on X,
∫ f dμi → ∫ f dμ
Starting with this topology and taking the Borel sets, M(X) becomes a measurable space.
It then turns out that M(X) is a standard Borel space iff X is!
In fact, M is what category theorists call a "monad" on the category of standard Borel spaces. I said what a monad is back in "week89", so I won't do it again, but here it involves the presence of god-given measurable maps
M(M(X)) → M(X)
and
X → M(X)
The first map is the most interesting: a probability measure on the space of probability measures of X gives a probability measure on X! In layman's terms: if you're uncertain about how uncertain you are, you might as well just say you're uncertain.
The second map just sends any point in X to the Dirac delta measure at that point. In layman's terms: if you're certain, you might as well say you're uncertain (just not very much). That is, if you're completely certain about something, you can still describe your state of knowledge by a probability distribution.
You can see some applications of this monad here:
15) David Corfield, Category theoretic probability theory II, http://golem.ph.utexas.edu/category/2007/02/category_theoretic_probability_1.html
16) Ernst-Erich Doberkat, Characterizing the Eilenberg-Moore algebras for a monad of stochastic relations, Universitat Dortmund, Fachbereit Informatik, Lehrstule fuer Software-Technologie, Memo 147. Also available at https://eldorado.uni-dortmund.de/bitstream/2003/2717/1/147.pdf
For more on standard Borel spaces in probability theory, try this:
17) K. R. Parthasrathy, Probability Measures on Metric Spaces, Academic Press, San Diego, 1967.
For standard Borel spaces and von Neumann algebras, try this:
18) W. Arveson, An Invitation to C*-Algebra, Springer, Berlin, 1976.
And for really hard-core results on standard Borel spaces and Polish groups, try this:
19) H. Becker and A. S. Kechris, Descriptive Set Theory of Polish Group Actions, Cambridge U. Press, Cambridge, 1996.
I can't imagine any of the normal readers of This Week's Finds will enjoy this book, but I could be wrong: there could be some really scary people who read this column.
Addenda: I thank Greg Egan, Benoit Jubin, Ted Nitz and Ultrawaffle for corrections and improvements. Originally I had a less complete table of probabilities for finite simple groups, and I begged my readers for help. Ted Nitz and Greg Egan stepped into save me.
Ted Nitz calculated the odds that a pair of elements in A4 generates the group and got 2/3:
I decided to take your challenge. For A4 the odds
are 96/144 = 2/3 that a pair generates. For reference,
the sage code that gave the probability is:
A4 = AlternatingGroup(4)
order = A4.order()
i = 0
j = 0
for g in A4:
for h in A4:
i += 1
if A4.subgroup([g,h]).order() == order:
j += 1
print (j,i)
j/i
It was blindingly fast for A4, and if it ever
finishes for A9, I'll let you know the probability
there.
-Ted
He later realized that the A9 calculation would take at least a century. Greg Egan wrote a Mathematica program based on a more efficient algorithm and got the answer in less than a day.
For more discussion, including the idea behind Egan's algorithm, visit the n-Category Café.
© 2008 John Baez
baez@math.removethis.ucr.andthis.edu

|
 
|

|