




|
 
|

|
1) Dan Christensen, Plots of roots of polynomials with integer coefficients, http://jdc.math.uwo.ca/roots/
2) John Baez, The beauty of roots, http://math.ucr.edu/home/baez/roots/
Click on the picture for bigger view. Roots of quadratic polynomials are in grey; roots of cubics are in cyan; roots of quartics are in red and roots of quintics are in black. The horizontal axis of symmetry is the real axis; the vertical axis of symmetry is the imaginary axis. The big hole in the middle is centered at 0; the next biggest holes are at ±1, and there are also holes at ±i and all the cube roots of 1.
You can see lots of fascinating patterns here, like how the roots of polynomials with integer coefficients tend to avoid integers and roots of unity - except when they land right on these points! You can see more patterns if you zoom in:
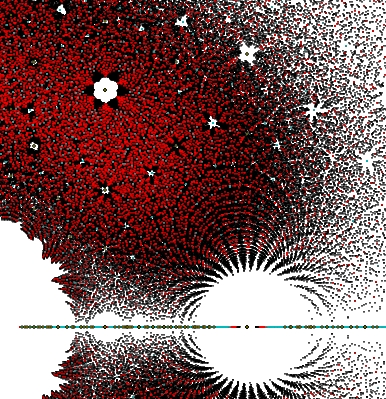
Now you see beautiful feathers surrounding the blank area around the point 1 on the real axis, a hexagonal star around exp(i π / 6), a strange red curve from this point to 1, smaller stars around other points, and more....
People should study this sort of thing! Let's define the set C(d,n) to be the set of all roots of all polynomials of degree d with integer coefficients ranging from -n to n. Clearly C(d,n) gets bigger as we make either d or n bigger. It becomes dense in the complex plane as n → ∞, as long as d ≥ 1. We get all the rational complex numbers if we fix d ≥ 1 and let n → ∞, and all the algebraic complex numbers if let both d,n → ∞.
But based on the above picture, there seem to be a lot of interesting conjectures to make about this set as d → ∞ for fixed n.
Inspired by the pictures above, Sam Derbyshire decided to to make a
high resolution plot of some roots of polynomials. After some
experimentation, he decided that his favorite were polynomials whose
coefficients were all 1 or -1 (not 0). He made a high-resolution plot
by computing all the roots of all polynomials of this sort having
degree 24. That's 224 polynomials, and about 24 ×
224 roots — or about 400 million roots! It took
Mathematica 4 days to generate the coordinates of the roots, producing
about 5 gigabytes of data. He then used some Java programs to create
this amazing image:
The coloring shows the density of roots, from black to dark red to
yellow to white. The picture above is a low-resolution version of the
original image, which is available as a 90-megabyte file on Dan's
website. We can zoom in to get more detail:
Next, here's the hole at i:
But the feathery structures as move inside the unit circle are
even more beautiful! Here is what they look near the real axis —
this plot is centered at the point 4/5:
3) Loki Joergenson, Zeros of polynomials with constrained coefficients, http://www.cecm.sfu.ca/~loki/Projects/Roots/
4) Eric W. Weisstein, MathWorld, Polynomial roots, http://mathworld.wolfram.com/PolynomialRoots.html
My colleague the knot theorist Xiao-Song Lin - sadly no longer with us - plotted the zeros of the Jones polynomial for prime alternating knots with up to 13 crossings, and you can see his pictures here:
5) Xiao-Song Lin, Zeros of the Jones polynomial, http://math.ucr.edu/~xl/abs-jk.pdf
You'll see that some of the patterns in his pictures just come from the patterns we see in the roots of polynomials with integer coefficients... since the Jones polynomial has integer coefficients.
This paper is also interesting:
6) Andrew M. Odlyzko and B. Poonen, Zeros of polynomials with 0,1 coefficients, L'Enseignement Math. 39 (1993), 317-348. Also available at http://dx.doi.org/10.5169/seals-60430
Odlyzko and Poonen proved some interesting things about the set of all roots of all polynomials with coefficients 0 or 1. If we define the set C(d,p,q) to be the set of roots of all polynomials of degree d with coefficients ranging from p to q, Odlyzko and Poonen are studying C(d,0,1) in the limit d → ∞. They mention some known results and prove some new ones: this set is contained in the half-plane Re(z) < 3/2 and contained in the annulus
1/Φ < |z| < Φ
where Φ is the golden ratio, (√5 + 1)/2. In fact they trap it, not just between these circles, but between two subtler curves. They also show that the closure of this set is path connected but not simply connected.
But from the pictures above, these ideas just scratch the surface of the wealth of patterns to be found and theorems to be proved!
Next, let me say a bit about the talks from the second day of the AMS session on homotopy theory and higher algebraic structures at UC Riverside. You can see videos of these talks here, or by clicking on the talk titles below:
7) Special session on homotopy theory and higher algebraic structures, AMS Western Section Meeting, November 7-8, 2009. Talks available as Quicktime videos at http://math.ucr.edu/~jbergner/amsriverside09.htm
It's been good for me trying to discuss all these talks - it's forced me to think about them a lot harder. I'm not sure how good it is for you, though: lots of ideas are flashing past without adequate explanation. Each talk could be the basis for a whole This Week's Finds. But I'm happy to get a chance to at least mention all sorts of ideas that would be fun to explore more deeply someday.
Eric Malm of Stanford University started the show bright and early 8:30 am on Sunday with a talk on "String topology and the based loop space". You can see the slides here:
8) Eric Malm, String topology and the based loop space, http://math.ucr.edu/~jbergner/ucr-st-present.pdf
In its original form, string topology studies the unbased loop space of an oriented d-dimensional manifold M. This is the space LM of all maps from a circle into M. In their fundamental paper on the subject:
9) Moira Chas and Dennis Sullivan, String topology, available as arXiv:math/9911159.
Chas and Sullivan showed that the homology groups of LM with degrees shifted by d:
Ai = Hi+d(LM)
are equipped with a graded-commutative product:
o: Ai ⊗ Aj → Ai+j
together with an operator
D: Ai → Ai+1
with D2 = 0. These satisfy a bunch of equations, which makes the degree-shifted homology of LM into a gadget called a "Gerstenhaber algebra". I explained such gadgets in "week220": they're precisely algebras of the homology of the little 2-cubes operad.
But the homology of the loop space has even more structure: it's a "Batalin-Vilkovisky algebra". That means that in addition to the above stuff, it has a Lie bracket of degree 1:
[·,·]: Ai ⊗ Aj → Ai+j+1
which gets along with the rest in a nice way. I also talked about these in "week220": they're precisely algebras of homology of the framed little 2-discs operad!
This is just the beginning of a big story. Malm's talk surveys this story and adapts the ideas of string topology to the based loop space of a manifold, using its relations to Hochschild homology. For some useful background here, try this book - or at least the very informative review:
10) Ralph L. Cohen, Kathryn Hess, and Alexander A. Voronov, String Topology and Cyclic Homology, Birkhauser, Boston, 2006. Review by Janko Latschev at http://www.ams.org/bull/0000-000-00/S0273-0979-09-01265-8/
Next, Laura Scull of Fort Lewis College spoke on "Orbifolds and equivariant homotopy theory". This is joint work she's doing with Dorette Pronk. Laura is an expert on equivariant homotopy theory: that's the kind of homotopy theory you do for spaces on which a group acts. Dorette is an expert on category theory. So it was natural for them to team up and tackle orbifolds!
Why? And what's an orbifold? Well, just as a manifold is built up from patches that look like Rn, an orbifold is built up from patches that look like Rn modulo the linear action of a finite group. So, most places it looks like a manifold, but it can have singularities of a mild sort here and there.
When people tried to define maps of orbifolds, they ran into a lot of trouble. Naive approaches led to a mess. It turns out there's a good reason for this. There's not really a nice category of orbifolds. But there's a nice 2-category of orbifolds!
The reason is that we shouldn't think of an orbifold as a set with extra structure. We should think of it as a groupoid with extra structure. The points of the orbifold are the objects of this groupoid. For a plain old manifold, we'd only have identity morphisms - so it's basically just a set. But for a more interesting orbifold, the singular points have extra automorphisms.
Everything likes to live in something bigger and fancier than itself. Groupoids, being categories, want to be objects of a 2-category. The same is true for orbifolds. However, there are extra subtleties due to the smooth structure on our orbifold. To deal with these, it's nice to treat orbifolds as "Lie groupoids" or "stacks". I could say a lot more, but instead I'll just refer you to this very readable paper:
11) Eugene Lerman, Orbifolds as stacks? Available as arXiv:0806.4160.
It begins by discussing easy approaches, then describes their flaws, and so on, leading up to the current state of the art. After this warmup, try:
12) Dorette Pronk and Laura Scull, Translation groupoids and orbifold Bredon cohomology, arXiv:0705.3249.
Then Anssi Lahtinen of Stanford University spoke about "The Atiyah-Segal completion theorem in twisted K-theory".
Twisted K-theory is fascinating to folks who like categorification, because it involves "U(1) gerbes", which are categorified U(1) bundles. Just as a U(1) bundle over a space can be defined by chopping a space into open sets Ui and giving U(1)-valued "transition functions" on the intersections Ui ∩ Uj, a U(1) gerbe over a space can be defined by chopping a space into open sets and giving transition functions
hijk : Ui ∩ Uj ∩ Uk → U(1)
If you have a U(1) gerbe, you can define "twisted vector bundles". These are like vector bundles, but where the transition functions gij satisfy the usual cocycle conditions only up to a phase, given by hijk. In other words, instead of the famous formula
gij gjk = gik
we just have
gij gjk hijk = gik
Given a space X, we can form its K-theory K(X) by taking the category of vector bundles and forming its Grothendieck group. We saw some Grothendieck group constructions last time! Here's how it goes this time. Take the category of vector bundles over X, say Vect(X). Then take the set of isomorphism classes of vector bundles. Then take formal linear combinations of these to get an abelian group, and then impose the equivalence relation
[M ⊕ N] = [M] + [N]
The result is an abelian group K(X) called the "K-theory" of X. And in fact it's a ring, since we can also take tensor products of vector bundles!
The Atiyah-Segal completion theorem concerns K(X) when X is the classifying space of a topological group G. As explained in "week151", this is a space BG with a principal G-bundle over it:
EG → BG
with the property that every other principal G-bundle over every other space is a pullback of this one. Given any representation of G, we can use the "associated bundle" trick to create a vector bundle over BG. So, we get a functor from the category of representations of G to the category of vector bundles over BG:
Rep(G) → Vect(BG)
Applying the Grothendieck group construction, this functor in turn gives a ring homomomorphism
R(G) → K(BG)
where R(G), the so-called "representation ring" of G, is the Grothendieck group of Rep(G).
The Atiyah-Segal theorem explains how this map from R(G) to K(BG) is almost - though not quite - an isomorphism. It's tempting to generalize this from K-theory to twisted K-theory... and that's what Anssi Lahtinen spoke about!
Next, Konrad Waldorf of UC Berkeley spoke on "String connections and supersymmetric sigma models":
13) Konrad Waldorf, String connections and supersymmetric sigma models, http://www.konradwaldorf.de/docs/riverside.pdf
14) Konrad Waldorf, String connections and Chern-Simons theory, available as arxiv:0906.0117.
His talk was a great introduction to some things I know and love, and some others that I'd never quite understood before... but loved at first sight now.
U(1) bundles over a space are classified by elements of its second cohomology with integer coefficients. U(1) gerbes are similarly classified by the third integral cohomology group. This story keeps on going! U(1) 2-gerbes are classified by the fourth cohomology, and so on. If you don't know what a 2-gerbe is, don't panic: just go back to my description of bundles and gerbes, and you can guess how the story continues.
But when M is a manifold, there's a nice way to get an element of its fourth integral cohomology group! If it's an oriented manifold, its oriented frame bundle is a principal SO(n) bundle. This has "characteristic classes"; the first interesting one is the "first Pontryagin class", which is an element in the fourth integral cohomology group of M. You can get a representative of this in deRham cohomology by picking a connection, taking its curvature 2-form F and multiplying the closed 2-form
tr(F ^ F)
by the right number. But in fact the first Pontryagin class lives in integral cohomology. So, any oriented 4-manifold automatically gives a 2-gerbe... but that's not the one we need here!
If M is equipped with a spin structure, its oriented frame bundle is equipped with a double cover that's a principal Spin(n) bundle. This too has characteristic classes. The first interesting one lives in the fourth integral cohomology group of M, and it has the property that when you multiply it by 2 you get the first Pontryagin class. (In integral cohomology there can be various different classes with this property, coming from different spin structures.)
So: every spin structure on M gives an element of the fourth integral cohomology group of M, and thus a 2-gerbe. This is called the "Chern-Simons 2-gerbe". The reason for this term is explained here:
15) Urs Schreiber, States of Chern-Simons theory, http://golem.ph.utexas.edu/category/2008/02/states_of_chernsimons_theory.html
There are lots of ways to think about "string structures" on a spin manifold M, but Waldorf advocated thinking of them as choices of trivialization of its Chern-Simons 2-gerbe. There may of course be none, or many. But the really nice thing about this viewpoint is that it gives a nice approach to "string connections".
Next, Søren Galatius of Stanford University gave a talk on "Monoids of moduli spaces of manifolds", explaining a paper with the same title:
16) Søren Galatius and Oscar Randal-Williams, Monoids of moduli spaces of manifolds, available as arXiv:0905.2855.
The goal of their work was to create a title with as many words beginning with "M" as possible... no, not really. In fact, it's a kind of continuation of this famous paper:
17) Søren Galatius, Ib Madsen, Ulrike Tillmann, and Michael Weiss, The homotopy type of the cobordism category, available as arXiv:math/0605249.
In item K of "week117" I explained how to turn any category into a topological space called its "classifying space". This construction has a nice generalization to "topological categories" - that is, categories where the set of morphisms from any object to any other is a topological space, and composition is continuous.
For example, a topological group G is the same as a topological category with one object and all morphisms being invertible. If we apply the construction to this example, we get the classifying space BG that I mentioned a while back.
The Galatius-Madsen-Tillmann-Weiss paper determined the homotopy type of the classifying space of the topological category of n-dimensional oriented cobordisms! The new work constructs a topological monoid that has the same classifying space - a nice simplification.
After lunch, Alissa Crans of Loyola Marymount University spoke on "2-Quandles: categorified quandles". A "quandle" is the sort of algebraic gadget when you axiomatize the properties of conjugation in a group. So, start with a group and define an operation of "left conjugation":
g > h = g h g-1
and an operation of "right conjugation":
h < g = g-1 h g
Then, figure out all the equations these obey, regardless of what group you've got! Clearly these operations are inverses of each other:
g > (h < g) = h = (g > h) < g
If you conjugate anything by itself, nothing happens:
g > g = g = g < g
But more interestingly, we also have
g > (h > k) = (g > h) > (g > k)
(k < h) < g = (k < g) < (h < g)
Conjugation distributes over itself! Do the calculation yourself and see! As far as I know, all equations obeyed by these operations follow from the ones I've listed... though I've never seen a proof, and I'd like to. These equations form the definition of a "quandle".
So, we may define a quandle in a very conceptual way as an algebraic structure where each element acts as a symmetry of that structure, and every element acts trivially on itself. Think about it.
But the magical thing about quandles is that they give invariants of tangles! The easiest way to start seeing this is by pondering braids. Given a quandle Q there's a way to turn any n-strand braid into a function
Qn → Qn
Here's how. In braids we can have two kinds of crossings:
\ / \ / / / \ / \and
\ / \ / \ / \ / \Let's think of each as giving a function from Q2 to itself. To do this, we let the quandle element labelling one strand act on the quandle element labelling the other, using our two kinds of conjugation:
g h \ / \ / / / \ / \ h g<hand
g h \ / \ / \ / \ / \ g>h gThe strand above acts on the strand below, following the general principle that the people higher up cause trouble for the people below them. Now, look at the third Reidemeister move, which says:
| / | | \ | \ / | | \ / \ | | \ / \ | | / \ | \ / \ / | | \ / \ / | | \ = \ | | / \ / \ | | / \ / \ | \ / | / \ / \ | | \ / \ | | / \ | \ | | / | | \ | | / |If we feed in three quandle elements on top, look what happens:
g h k g h k | / | | \ | \ / | | \ / \ | | \ / \ | | h>k/ \ | \ / \ / | | \ / \ / | |g>h \ = \ | | / \ / \ | | / \ / \ | \ /g>k | / \ / \ | | \ / \ | | / \ | \ | | / | | \ | | / | * g>h g * g>h gLook at the strand marked with an asterisk! On the left it should be labelled by
(g > h) > (g > k)
On the right it should be labelled by
g > (h > k)
But thanks to the self-distributive law, these are equal! Similarly, the equation
g > (h < g) = h = (g > h) < g
handles the second Reidemeister move:
\ / | | \ / \ / | | \ / / | | \ / \ | | / \ / \ = | | = / \ \ / | | \ / \ / | | \ / \ | | / / \ | | / \ / \ | | / \while the equation
g > g = g = g < g
handles the first Reidemeister move. The first Reidemeister move is not really about about braids - it's about tangles:
| /\ | | /\ | / \ | | / \ \ / \ | \ / \ \ / | | \ / | \ | = | = / | / \ | | / \ | / \ / | / \ / | \ / | | \ / | \/ | | \/ | | |So, there's a deep relation between crossings in tangles and conjugation in groups, captured by the quandle axioms. And the quandle axioms also cover Lie algebras, with self-distributivity corresponding to the Jacobi identity:
16) J. Scott Carter, Alissa Crans, Mohamed Elhamdadi and Masahico Saito, Cohomology of categorical self-distributivity, available as arXiv:math/0607417.
It's possible to explain this relation a lot more deeply than I just did... but anyway, what Alissa did is start categorifying this relation. Together with the topologists Carter and Saito, she's studying "2-quandles", which should relate 2-tangles to conjugation in 2-groups.
Next, Chad Giusti of the University of Oregon spoke on "Unstable Vassiliev theory":
17) Chad Giusti, Unstable Vassiliev theory, http://math.ucr.edu/~jbergner/RiversideTalk.pdf
The goal here is to understand the space of "long knots". A long knot is a curve in R3 that goes on forever and is a vertical straight line outside some compact set. So, it can get knotted around in the middle. One nice thing about long knots is that there's a multiplication defined on them, by sticking them end-to-end.
If you know about tangles, a long knot is just another way of thinking about a one-strand tangle with a strand coming in at top and going out at bottom. Then the multiplication on long knots is a special case of the composition of tangles.
(We can define even more operations if we work with "thickened" long knots. In fact, the space of these forms an algebra of the little 2-cubes operad! This gives a mystical relation between thickened long knots and Gerstenhaber algebras. I explained this near the end of "week220".)
Anyway, the part of Giusti's talk that I understood best, and therefore liked the most, was a neat combinatorial description of the space of long knots. He calls them "plumbers' knots", because they're like pipes that move only along the x, y, or z directions... for details, see his slides!
Then Robin Koytcheff of Stanford University gave a somewhat related talk on "A homotopy-theoretic view of Bott-Taubes integrals and knot spaces":
18) Robin Koytcheff, A homotopy-theoretic view of Bott-Taubes integrals and knot spaces, http://math.ucr.edu/~jbergner/RKslidesUCR.pdf
He began with a nice introduction to the Bott-Taubes approach to Vassiliev theory. Then he gave a great description of how the little 2-cubes operad acts on the space of thickened long knots, and how one can use this to underand the homology of this space. Then he discussed how to combine these ideas. For more details, see:
19) Robin Koytcheff, A homotopy-theoretic view of Bott-Taubes integrals and knot spaces, Alg. Geom. Top. 9 (2009), 1467-1501. Also available as arXiv:0810.1785.
Next, Chris Douglas of U.C. Berkeley gave talk charmingly entitled "3-categories for the working mathematician" - unfortunately no video for this one. It's great to see how weak 3-categories are making their way into applications. Douglas is working with Arthur Bartels and Andre Henriques on their applications to "conformal nets" - that is, algebras of local observables in conformal field theory. The bulk of Douglas' talk involved a kind of hieroglyphic notation for operations and equations in a definition of weak 3-category. This definition is close to the existing definitions of "tricategory", but not exactly the same - at least, not superficially. It's probably equivalent.
Finally, Scott Morrison and Kevin Walker gave a 2-part talk on "blob homology" - a great introduction to their big paper in progress:
20) Scott Morrison and Kevin Walker, Blob homology slides: http://tqft.net/UCR-blobs1 and http://tqft.net/UCR-blobs2
21) Scott Morrison and Kevin Walker, The blob complex. Draft available at http://tqft.net/papers/blobs.pdf
The clever idea here is to use manifolds to provide a quick and practical definition of "n-categories with duals" - thus short-circuiting, at least temporarily, the need to prove some big conjectures linking this algebraic concept to topology. With this definition, they're able to define and study "blob homology": that is, a kind of homology for manifolds with coefficients in a linear n-category with duals!
This includes ordinary TQFTs and also Hochschild homology as special cases. So, it's a big deal, and I'm sure we'll be seeing more of it in the years to come.
Next week I'll start a series of This Week's Finds on rational homotopy theory. This is a great subject with connections to pretty much everything: deformation theory, Lie n-groups and Lie n-algebras, classical mechanics, supergravity and more! So stay tuned....
Addenda: I thank Toby Bartels for some improvements, and Ralf Bader for a link to Odlyzko and Poonen's paper.
For more discussion visit the n-Category Café.
The author feels that this technique of deliberately lying will actually make it easier for you to learn the ideas. - Donald Knuth
© 2009 John Baez
baez@math.removethis.ucr.andthis.edu

|
 
|

|