week284

November 24, 2009

This Week's Finds in Mathematical Physics (Week 284)

John Baez

A couple of weeks ago there was a meeting of the American Mathematical Society here at UC Riverside. Mathematicians flooded in from across the western US and even further. They gave hundreds of 20-minute talks, drank lots of coffee, ate a few too many pastries, and chatted with each other. Julie Bergner and I ran a session at this conference. My student Chris Rogers took videos of the talks in our session, and you can see them here:

1) Special session on homotopy theory and higher algebraic structures, AMS Western Section Meeting, November 7-8, 2009. Talks available as Quicktime videos at http://math.ucr.edu/~jbergner/amsriverside09.htm

These talks add up to a nice look at recent work on homotopy theory, n-categories, and categorification - some of my favorite subjects. So, I'd like to quickly summarize each talk and give some links to related papers.

But first: something a bit less technical!

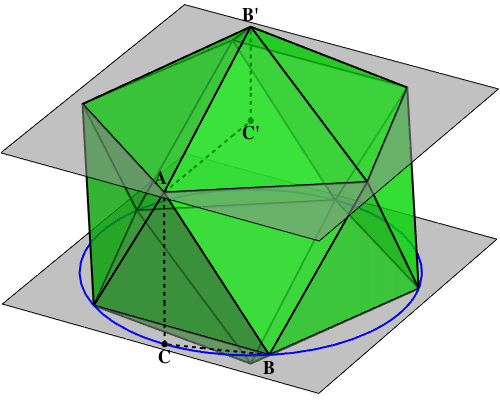
Last week I asked you to provide a nice proof of Proposition 10 from the last book of Euclid - the one where he constructs the Platonic solids. Euclid uses this proposition to construct the icosahedron, but it's appealing in its own right. In modern language it says:

Inscribe a regular pentagon, hexagon and decagon in a circle, and call their side lengths P, H and D. Then
P² = H² + D².

I find this fascinating. One reason is that it's simple but far from obvious. Another is that it's secretly all about the golden ratio and its role in 5-fold symmetry. And another is that Euclid's proof is ingenious but not very intuitive - so it seems there should be a better proof. For example, a proof that uses the icosahedron!

(Last week I gave a proof using algebra and trigonometry, but it wasn't terribly interesting.)

The science fiction writer Greg Egan said that Euclid's proof was "really dazzling, but it made me feel like he'd pulled a coin out from behind my ear." Egan wrote a modernized version of this proof, which you can see in the Addenda to "week283". But he then went on to give a number of other proofs, including two that I like a lot better:

2) nLab, Pentagon-decagon-hexagon identity, http://www.ncatlab.org/nlab/show/pentagon+decagon+hexagon+identity

One of these proofs uses the icosahedron. As I'd dreamt in "week283", it proceeds by showing that two right triangles hiding in the icosahedron are congruent. Namely, the triangles ABC and AB'C' shown here:

The other proof is purely 2-dimensional. For this, Egan starts by recalling Proposition 9 from the same book of Euclid. This result states the main property of the "golden triangle".

What's a golden triangle? Well, if you draw a regular pentagon and connect each vertex to every other, you'll get a pentagram in a pentagon - but you'll also see lots of tall skinny isosceles triangles:

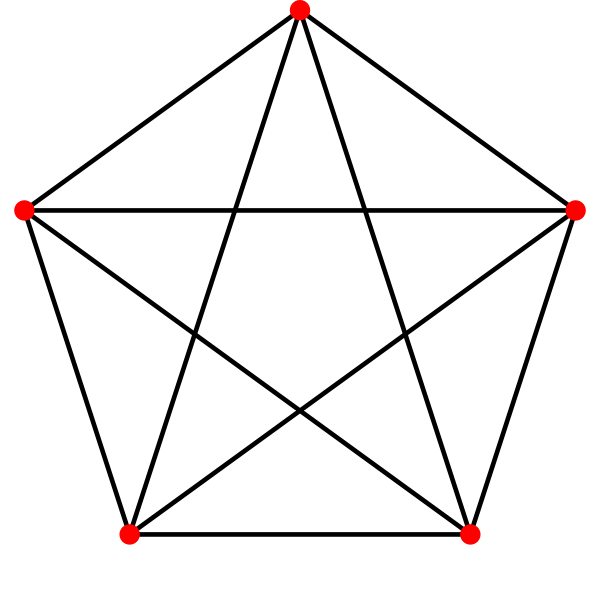
These are "golden triangles". They have angles of 36 degrees, 72 degrees, and 72 degrees. How many are there in this picture?

In Proposition 9, Euclid shows that for a golden triangle, the ratio of the edge lengths is the golden ratio. Actually he shows something equivalent, roughly this:

Inscribe a regular hexagon and decagon in a circle. Then the ratio of their side lengths is the golden ratio:
D/H = φ = (-1 + √ 5)/2

Why is this equivalent? Well, if you inscribe a regular decagon in a circle and draw lines from its center to its vertices, you get ten golden triangles. The long edge of each triangle is H, since the radius of the circle equals the edge of an inscribed circle. The short edge is D.

Oddly, Euclid does not use Proposition 9 to prove Proposition 10, even though it's relevant and it comes right before! But Egan's proof uses it. Check out the nLab entry for details and pretty pictures. I think it's great that 21st-century technology is being used to improve a proof dating back to 300 BC.

Now... on to the talks on homotopy theory and higher algebraic structures! I'm afraid the length of my summaries will be proportional to how much I understood. You can click on the talk titles to see the videos.

Bright and early at 8 am on Saturday morning, Aaron Lauda kicked off the special session with a talk on "Categorifying quantum groups". Luckily he'd come from the east coast, so he was wide awake, and his energy was contagious.

From the very beginning of This Week's Finds you can see that I was interested in Crane and Frenkel's dream of categorified quantum groups. Now this dream is coming true! Aaron gave a great series of talks on this subject in Kyoto this February, and you can see them all here:

3) Aaron Lauda, Kyoto lectures:

Categorification of quantum sl(2),
Categorification of one half of the quantum group,
Categorification of quantum sl(n),
Cyclotomic quotients of the rings R(ν).

Available at http://www.math.columbia.edu/~lauda/talks/kyoto/

At Riverside he explained what people often call the "Khovanov-Lauda algebra" R associated to a simply laced Dynkin diagram. This gives a way of categorifying the "positive part" of the corresponding quantum group.

4) Mikhail Khovanov and Aaron Lauda, A diagrammatic approach to categorification of quantum groups I-III, available as arXiv:0803.4121, arXiv:0804.2080, and arXiv:0803.3250.

Huh? Well, just as the group of matrices has a subgroup consisting of upper triangular matrices and a subgroup consisting of lower triangular matrices, so any quantum group breaks into a "positive part" and a "negative part", with a bit of overlap. It's easier to categorify either of these parts than the whole thing, because when you deal with the whole thing you get formulas involving negative numbers, which are harder to categorify.

How does the algebra R help us categorify the positive part of a quantum group? Or, for that matter, the negative part? - the two parts look alike, so we randomly choose to work with the positive part.

The answer is simple: we just form the category of representations of R!

But how do we get back from this category to the positive part of the quantum group? In other words, how do we "decategorify"? Again, the answer is simple: just take its Grothendieck group! A bit more precisely: we take the category of finitely generated projective R-modules, and look at isomorphism classes of these, and let these generate an abelian group with relations saying that direct sums should act like sums:

[M ⊕ N] = [M] + [N]

This gives a certain "integral form" of the positive part of the quantum group. If we tensor this with the complex numbers, we get the more familiar complex version of the quantum group.

One of the great virtues of the Khovanov-Lauda algebra is that it has a nice presentation, with generators and relations given in terms of pretty pictures. This is great for computations. However, the presentation is a bit complicated, so I can't help but wonder where it came from. Maybe there's some nice geometry underlying the whole story?

Indeed, Aaron has also worked on more geometrical approaches to categorifying quantum groups, at least for the simplest of simple Lie algebras, namely sl(2):

5) Aaron Lauda, A categorification of quantum sl(2), available as arXiv:0803.3652.

6) Aaron Lauda, Categorified quantum sl(2) and equivariant cohomology of iterated flag varieties, available as arXiv:0803.3848.

But there are also lots of other people tackling the geometrical side of the story. One of these is Anthony Licata of Stanford University! Right after Aaron, he gave a talk on "Categorification via quiver varieties", based on these papers:

6) Sabin Cautis, Joel Kamnitzer, and Anthony Licata, Coherent sheaves and categorical sl(2) actions, available as arXiv:0902.1796.

7) Sabin Cautis, Joel Kamnitzer, and Anthony Licata, Derived equivalences for cotangent bundles of Grassmannians via categorical sl(2) actions, available as arXiv:0902.1797.

The first paper studies various notions of a categorified representation of sl(2). The second studies an example coming from cotangent bundles of Grassmannians. That's a lot of math to compress into a 20-minute talk! Luckily Licata was able to do it, by leaving out all but the most fundamental concepts.

His work follows the philosophy that "geometrization leads to categorification". This is based on a branch of math called "geometric representation theory".

The name here is a bit misleading, since a lot of group representation theory is geometrical in nature. For example, if we have a group G acting as symmetries of a space X, we get a representation of G on the vector space of functions on X. And there are many sophisticated refinements of this idea. But "geometric representation theory" is different. It gets representations in unexpected new ways, often starting from the cohomology of a space X on which G does not act!

I think this is the best place to start learning geometric representation theory:

8) Neil Chriss and Victor Ginzburg, Representation Theory and Complex Geometry, Birkhauser, Boston, 1997.

I've spent some time on this book, but not enough. The results still seem strange to me. They're like an outcropping of unfamiliar rocks poking through the strata of mathematics that make sense to me. I'd need to dig deeper to get a sense of what's going on down there. Just thinking about this makes me itch to understand geometric representation theory better. I know specific results, but not the overall pattern!

You expect, for example, to get representations of sl(2) whenever you build vector spaces starting from C². Why? Because the group SL(2) acts as symmetries of C², and thus on any vector space functorially constructed from it. But Ginzburg found some unexpected new ways of getting representations of sl(2)... and Licata sketched how this lets you categorify these representations.

Here's the example Licata explained. The group SL(2) acts on C² and thus on its nth tensor power. Everyone knows that. But we can also get this representation in an unexpected way. Start with the space of all k-dimensional subspaces of Cⁿ. This is called the "Grassmannian" Gr(k,n). Form a vector space by taking the cohomology of the cotangent bundle T*Gr(k,n). Then take the direct sum of these vector spaces as k goes from 0 to n.

We get a big fat vector space. But here's the cool part: Ginzburg figured out how to make this big fat space into a representation of sl(2)! And this representation is isomorphic to the nth tensor power of C².

The trick is to get operators on cohomology groups that satisfy the relations for sl(2). As usual in geometric representations theory, we build these using "spans". These are setups where you have three spaces and two maps like this:

                     S
                    / \
                   /   \
                 P/     \Q
                 /       \
                v         v 
               X           Y

We can pull back cohomology classes along P, and then if we're lucky we can push them forward along Q, getting an operator from the cohomology of X to the cohomology of Y. I explained why spans are geometrically interesting back in "week254".

Anyway, so Ginzburg got a representation of sl(2) using this trick. To categorify this representation, Licata replaced the cohomology of T*Gr(k,n) by a category called the "bounded derived category of coherent sheaves" on this space. That's a plausible strategy, because it's known quite generally that for any smooth variety X you can take the Grothendieck group of this category and get back the cohomology of X.

In fact, if you have no idea what a "bounded derived category of coherent sheaves" is, this should make you want to know! It's a categorification of cohomology. Here's a good place to start learning more:

9) Andrei Caldararu, Derived categories of sheaves: a skimming. Available at http://www.math.wisc.edu/~andreic/publications/lnPoland.pdf

Next came two talks on another approach to categorification, called "groupoidification". This involves replacing vector spaces by groupoids and linear operators by spans of groupoids. The reverse process, "degroupoidification", is an entirely systematic procedure for squashing groupoids into vector spaces and spans of groupoids into linear operators. I explained how this works back in "week256".

First Alex Hoffnung spoke about "A categorification of the Hecke algebra". The idea here is to see the Hecke algebras associated to Dynkin diagrams as a special case of a much more general construction: the Hecke bicategory.

Given a finite group G, the Hecke bicategory Hecke(G) is a gadget where:

objects are finite G-sets;
the groupoid of morphisms from X to Y is the weak quotient (X x Y)//G.

Here the "weak quotient" is a bit like the ordinary quotient of a set by a group action - but instead making elements equal when there's a group element mapping one to another, we make them isomorphic. So, it's a groupoid. (For more details, see "week249".)

Using a systematic procedure for turning groupoids into vector spaces, we can squash Hecke(G) down into a category that has a mere vector space of morphisms from X to Y.

Now, a category where the set of morphisms between any two objects is a vector space, and composition is linear in each argument, is sometimes called an "algebroid". Why? Because an algebroid with one object is an algebra - in the same way that a groupoid with an object is a group.

So, the Hecke bicategory gets squashed down into something that deserves to be called the "Hecke algebroid" of G.

Now pick a finite field and a Dynkin diagram. This gives a simple algebraic group G and a very important G-set X, called the "flag variety" of G. Take the Hecke algebroid of G and concentrate your attention on the morphisms from X to X. By what I've said, these form an algebra. And this is the famous "Hecke algebra" associated to our Dynkin diagram! The usual parameter q that appears in the definition of a Hecke algebra is just the number of elements in our finite field.

Alex Hoffnung illustrated his talk with a picture of a cow jumping over the moon, wearing a bowtie, and getting killed by a lightning bolt. You'll have to watch his talk to see how this is relevant. The otherwise excellent slides do not explain this joke:

8) Alex Hoffnung, A categorification of the Hecke algebra, http://math.ucr.edu/~alex/hecke.pdf

Then Christopher Walker gave a talk on "A categorification of Hall algebras". Unfortunately, the cameraman showed up a little late, so the video of his talk starts after a couple of minutes have gone by. Fortunately, the next week he passed his oral exam at UCR with a longer version of the same talk! So, check out the slides for that:

9) Christopher Walker, A categorification of Hall algebras, http://math.ucr.edu/~cwalker66/Oral_Exam_talk_11_10.pdf

But here's the idea in a nutshell. Take a simply-laced Dynkin diagram. Draw arrows on the edges to get a directed graph. Let this graph freely generate a category, say Q. There's a groupoid of "quiver representations", where:

objects are functors from Q to the category of vector spaces over some fixed finite field;
morphisms are natural isomorphisms.

Next, apply our systematic procedure for turning groupoids into vector spaces! In the case at hand, we get the positive part of the quantum group associated to our Dynkin diagram. The usual parameter q that appears in the definition of a quantum group is just the number of elements in our finite field.

(Here we see a difference from the Khovanov-Lauda approach, where q is a formal variable.)

So far, this is actually an old theorem of Ringel. The trick is to use it to systematically "groupoidify" quantum groups - or at least their positive parts - and then work with them at the groupoidified level. And that's what Christopher is doing now!

His talk explains more, and you can learn more about groupoidification and its applications to Hecke and Hall algebras here:

10) John Baez, Alex Hoffnung and Christopher Walker, Higher-dimensional algebra VII: groupoidification. arXiv:0908.4305.

Next came three talks on homotopy theory.

Jonathan Lee of Stanford University spoke on "Homotopy colimits and the space of square-zero upper-triangular matrices". You can see slides of his talk here:

11) Jonathan Lee, Homotopy colimits and the space of square-zero upper-triangular matrices, http://math.stanford.edu/~jlee/homotopy-talk.pdf

He talked about his work on a conjecture of Halperin and Carlsson. There are different ways to formulate it, but here's a nice topological way. Suppose the torus Tⁿ acts freely on a finite CW complex X. Then the sum of the Betti numbers of X is at least 2ⁿ. There's also a nice purely algebraic way!

Nitu Kitchloo of UC San Diego spoke on "Universal Bott-Samelson resolutions". As a warmup for this, I should just tell you what a Bott-Samelson resolution is.

I spoke quite a bit about Schubert cells in "week184" and subsequent Weeks. The idea is that if you have a Grassmannian, or more generally any space of the form G/P where G is a simple Lie group and P is a parabolic subgroup, it comes equipped with a decomposition into cells. These are the "Schubert cells". They're packed with fascinating algebra, geometry, and combinatorics. They are, in fact, algebraic varieties! But, they're not smooth - they're singular.

And so, if you were an algebraic geometer, you might be tempted to "resolve" their singularities: that is, find a smooth variety that maps onto them in a nice way. Bott and Samelson figured out a way to do this... but not just one way. So, you might want to find a "best" - or more technically, a "universal" - Bott-Samelson resolution. And that's what Nitu Kitchloo talked about.

After lunch, Maia Averett of Mills College started the show with a talk on "Real Johnson-Wilson theories", based on work with Nitu Kitchloo and Steve Wilson. This was heavy-duty homotopy theory of the sort I can only gape at in awe. It's part of a big network of ideas which include elliptic cohomology and higher steps in the "chromatic filtration" - topics I discussed back in "week197" and "week255".

You can see some slides here:

12) Maia Averett, Real Johnson-Wilson theories, http://www.math.uchicago.edu/~fiore/1/Averett.pdf

Real Johnson-Wilson theories are certain generalized cohomology theories (see "week149"). They can be thought of as "higher" versions of real K-theory. Thanks to complex conjugation, the group Z/2 acts on the complex K-theory spectrum KU, and if we take the homotopy fixed points we get the real K-theory spectrum KO. But complex K-theory is just the first of the Johnson-Wilson theories!

To get the others, you do something roughly like this. (I'm reading some stuff to figure this out, and I could be getting it wrong.) The spectrum for complex cobordism theory is called MU. If you localize this at 2 you get something called the Brown-Peterson spectrum, BP. The generalized cohomology for this, applied to a one-point space, is a ring on infinitely many generators. If you do some trick to kill off all the generators above the nth, you get the nth Johnson-Wilson theory. And since this was built starting from complex cobordism theory, complex conjugation acts on it. So, we can take the homotopy fixed points, you get the nth "real" Johnson-Wilson theory.

Emin Tatar of Florida State University spoke on "Abelian sheaves and Picard stacks":

13) A. Emin Tatar, Abelian sheaves and Picard stacks, http://www.math.ucr.edu/~jbergner/tatar_slides.pdf

This talk assumed a fair amount of background, so let me just sketch a bit of that background. For more details, try this:

14) A. Emin Tatar, Length 3 complexes of abelian sheaves and Picard 2-stacks, available as arXiv:0906.2393.

You've probably heard me talk about 2-groups. These are categorified groups. More precisely, they're categories with a tensor product, where every morphism has an inverse and every object x has an inverse with respect to the tensor product: that is, an object x* such that

x ⊗ x* ≅ 1

and

x* ⊗ x ≅ 1

2-groups are a great way to dip your toe in vast ocean of n-category theory. They're one step to the right of groups in the n-groupoid version of the periodic table:

                   k-tuply groupal n-groupoids

              n = 0           n = 1             n = 2

k = 0         sets           groupoids        2-groupoids

k = 1        groups          2-groups          3-groups

k = 2        abelian         braided           braided
             groups          2-groups          3-groups

k = 3         " "            symmetric         sylleptic
                             2-groups          3-groups

k = 4         " "             " "              symmetric
                                               3-groups

k = 5         " "             " "                "  "

Just as abelian groups are especially simple and nice, so are symmetric 2-groups. Where an abelian group obeys the equation

xy = yx

a symmetric 2-group instead has an isomorphism

S_x,y: x ⊗ y → y ⊗ x

with the property that doing it twice gives the identity:

S_y,x S_x,y = 1

Lately people have been generalizing a lot of math from abelian groups to symmetric 2-groups. See "week266" for more, and especially this:

15) Mathieu Dupont, Abelian categories in dimension 2, Ph.D thesis, l'Universite Catholique de Louvain, 2008. Available as arXiv:0809.1760. Original available in French at http://hdl.handle.net/2078.1/12735

But the simplest symmetric 2-groups are those with this extra property:

S_x,x = 1

Emin Tatar calls these "Picard categories", following Deligne.

(I would like to call these "Picard 2-groups", but that might be confusing, since "Picard group" already means something quite different. To add to the confusion, it seems that Dupont and others use "Picard category" as a synonym for symmetric 2-group!)

Anyway, there's a nice description of Picard categories. They're all equivalent to the 2-groups that you get from 2-term chain complexes of abelian groups!

It's nice to see how this works. Take a 2-term chain complex of abelian groups:

    d
A <--- B

Then there's a category where the objects are elements of A, and the morphisms from a to a' are elements b of B with

a' = a + db

Addition lets you compose morphisms - but it also lets you add objects, making this category into a 2-group. And the abelianness makes this not just a symmetric 2-group, but even a Picard category!

But the cool fact is that every Picard category is equivalent to one arising this way.

In fact, Deligne went a lot further. There's a general principle that anything really important that you can do with sets, you can also do with sheaves of sets. So, you might guess that anything really important you can do with categories, you can do with sheaves of categories.

That's morally correct - but not quite technically correct, because we need to take the definition of "sheaf" and replace some equations by isomorphisms to make it applicable to categories. If we do this, we get the concept of a "stack".

Then everything works great. Just as we can talk about sheaves of abelian groups, we can talk about stacks of Picard categories - or "Picard stacks", for short. And the cool fact I mentioned generalizes to these! Every Picard stack is equivalent to one that comes from a 2-term complex of sheaves of abelian groups. This was proved by Deligne quite a while ago - it's Lemma 1.4.13 here:

15) Pierre Deligne, La formule de dualité globale, Sem. Geom. Algébrique Bois-Marie 1963/64, SGA 4 III, No. XVIII, Springer Lecture Notes in Mathematics 305, 1973, pp. 481-587. Also available at http://www.math.polytechnique.fr/~laszlo/sga4/SGA4-3/sga43.pdf

But you can also see a different proof in Proposition 8.3.2 of this paper by Tatar's advisor and Behrang Noohi:

16) Ettore Aldrovandi and Behrang Noohi, Butterflies I: morphisms of 2-group stacks, Adv. Math. 221 (2009), 687-773. Also available as arXiv:0808.3627.

Now, what did Tatar do? He categorified all this stuff once more! In other words, he defined Picard 2-stacks, and proved that every Picard 2-stack is equivalent to one coming from a 3-term chain complex of sheaves of abelian groups!

Next, David Spivak of the University of Oregon spoke on "Mapping spaces in quasi-categories". Quasicategories are a nice way to formalize the idea of an (∞,1)-category - that is, an ∞-category where all the morphisms above the 1-morphisms are weakly invertible. Technically, quasicategories they're just simplicial sets with a special property. So, one can study them using all the simplicial machinery that homotopy theorists have been developing over the years.

However, there are many other ways to formalize (∞,1)-categories. A classic one is "simplicial categories". These are just categories "enriched over simplicial sets". In other words, they have a simplicial set of morphisms from any object to any other object, and composition is a map of simplicial sets.

(If I'd been willing to use this jargon earlier, I could have defined an algebroid to be a category "enriched over vector spaces". However, I didn't want to scare away all my readers - at least, not so soon! By this point I figure all the wimps are gone.)

A while back, Jacob Lurie described a way to turn any quasicategory into a simplicial category - see for example Remark 1.1.5.18 here:

16) Jacob Lurie, Higher Topos Theory, Annals of Mathematics Studies 170, Princeton University Press, Princeton, NJ, 2009. Also available as arXiv:math/0608040.

This involves taking two vertices of our quasicategory - which, remember, is just a simplicial set with some properties - and cooking up a simplicial set of "morphisms" from one to the other. Recently Daniel Dugger and David Spivak have come up with another way:

17) Daniel Dugger and David I. Spivak, Rigidification of quasi-categories, available as arXiv:0910.0814.

18) Daniel Dugger and David I. Spivak, Mapping spaces in quasi-categories, available as arXiv:0911.0469.

And that's what David explained in his talk!

The day concluded with two talks of a somewhat more concrete nature. Ben Williams of Stanford University spoke on "An application of A¹-homotopy theory to problems in commutative algebra". Like Jonathan Lee, the problems he was considering included the conjecture of Halperin and Carlsson that I mentioned before. But, he used ideas from A¹-homotopy theory. So, let me say a word about that.

I actually tried my hand at explaining A¹-homotopy theory near the end of "week255". It's an attempt to do homotopy theory for algebraic varieties, where homotopies are parametrized not by the interval but by the line - since the line is an algebraic variety. Algebraic geometers call the line A¹, just to make the rest of us feel dumb.

In his work on A¹-homotopy theory, Voevodsky studied certain cohomology groups for a variety X, called "motivic cohomology groups". The curious thing is that they're bigraded instead of just graded. Instead of getting cohomology groups H^p(X,A) with coefficients in an abelian group A, we get cohomology groups H^p,q(X,A).

Why is this? I wish I understood it better... but I think it's basically because we could already define cohomology groups for varieties without this extra notion of homotopies parametrized by the line... but now we can also define them with that notion, as well. The old cohomology groups were defined using sheaves; the new one is defined using simplicial sheaves, and the simplicial aspect of these sheaves gives a new grading.

And indeed, Voevodsky was able to relate motivic cohomology to another bigraded gadget: the "higher Chow groups" of the variety X. These are a lot easier to define, so let me describe those. Consider the free abelian group generated by irreducible subvarieties of codimension k in

X × Δⁿ

where Δⁿ is the n-simplex. (Actually, we should only use subvarieties that hit the faces of the simplex "properly".) As we let n vary, we get a simplicial abelian group. But a simplicial abelian group is just a chain complex in disguise! - I explained how in item H of "week116".

So, define the higher Chow groups to be the homology groups of this chain complex. They depend on two parameters: the "simplicial" dimension n, but also the "geometrical" codimension k.

Obviously it would take me a few years of hard work to get from this to the point of actually understanding Ben William's talk!

Finally, Christian Haesemeyer of UCLA wrapped up the day with a talk "On the K-theory of toric varieties". For quite a while I've been meaning to explain toric varieties, which are a marvelous playground for exploring algebraic geometry. Roughly: just as an algebraic variety looks locally like the solution set of a bunch of polynomial equations, a toric variety looks like the solution set of a bunch of polynomial equations where you're not allowed to add, only multiply!

This restriction makes them marvelously tractable - you can easily describe them using pictures called "fans". Here's a nice informal explanation of how this works:

19) David Speyer, Toric varieties and polytopes, http://sbseminar.wordpress.com/2009/02/09/toric-varieties-and-polytopes/

Toric varieties and fans, http://sbseminar.wordpress.com/2009/02/18/toric-varieties-and-fans/

Once you become a fan of fans - and it's easy to do - you can't resist wanting to take all your favorite invariants of algebraic varieties and see what they look like for toric varieties. Like K-theory!

Hmm. I'm only described the first day's worth of talks, and it's taken more than one day. And I'm left with a lot of questions. For example:

Aaron Lauda wrote: "It turns out, at least in the simply-laced case, that our algebras are also isomorphic to the Ext algebras between simple perverse sheaves on the Lusztig quiver variety. Lusztig's bilinear form can be seen as taking the graded dimension of this Ext algebra, so it is natural that there is a relationship between the two constructions." Can someone say more about what's going on here? Please don't assume I understand what Aaron told me!
How does the representation Licata describes, involving the cohomology of the cotangent bundle of the Grassmannians Gr(n,k) for k between 0 and n, fit into a more general story? I think the disjoint union of these Grassmannians should be thought of as the space of 1-stage "Springer flags" in n dimensions - where an m-stage Springer flag is a chain of m subspaces of Cⁿ. I vaguely recall that it's interesting to generalize by letting m be arbitrary. And I think that an even more general story - where we pass from sl(2) to sl(N) - involves Springer flags in the category of quiver representations. Is this right? What's the big picture?
Is my account of Johnson-Wilson theories accurate? What are the most important things that I left out here?
What's "motivic" about Voevodsky's motivic cohomology? Does he propose a definition of motives? How is it related to Grothendieck's conception of motives? How, from this viewpoint, can we see that motivic cohomology should be bigraded?
What other things should I have said, but didn't?

If you have answers, or just other questions, please visit the n-Category Café.

Happy Thanksgiving!

Addenda: I thank Toby Bartels yet again for catching a messed-up link, and David Corfield for catching some typos.

For more discussion visit the n-Category Café. Please try to answer my questions above!

There are two fundamental and completely different examples in group theory: the "symmetric group" of permutations of n objects, and the "linear group" of n by n matrices over a field. Lusztig says the linear group is a quantum version of the symmetric group, with the value of Planck's constant telling you which field you're looking at. He has made that idea precise in a thousand beautiful ways for the past 30 years. - David Vogan