




|
 
|

|
We had a great AMS meeting this weekend at UCR, with far too many interesting talks going on simultaneously. For example, there were two sessions on math related to knot theory, one on operator algebras, one on noncommutative geometry, and one on homotopy theory and higher algebraic structures! If I could clone myself, I'd have gone to all of them.
I'd like to discuss some of the talks, and maybe even point you to some videos. But the videos aren't available yet, so for now I'll just summarize my own talk on "Who Discovered the Icosahedron", and some geometry related to that. I'll conclude with a puzzle.
But first - the astronomy pictures of the week!
Galaxies are beautiful things, and there are lots of ways to enjoy them. Here's the Milky Way in visible light - a detailed panorama created from over 3000 individual pictures, carefully calibrated to show large dust clouds:
1) Axel Mellinger, All-sky Milky Way panorama 2.0, http://home.arcor.de/axel.mellinger/
You can see even more structure in this infrared panorama of the Milky Way, created by the Spitzer Space Telescope:
2) Astronomy Picture of the Day, GLIMPSE the Milky Way, http://apod.nasa.gov/apod/ap051216.html
The bright white splotches are star-forming regions. The greenish wisps are hot interstellar gas. The red clouds are dust and organic molecules like polycyclic aromatic hydrocarbons (see "week258"). The darkest patches are regions of cool dust too thick for Spitzer to see through.
But here's my favorite: the Andromeda Galaxy in viewed in ultraviolet light:
3) Astronomy Picture of the Day, Ultraviolet Andromeda, http://apod.nasa.gov/apod/ap090917.html
This was taken by Swift, NASA's ultraviolet satellite telescope. At this frequency, young hot stars and dense star clusters dominate the view. It's sort of ghostly looking, no?
Now for my talk on the early history of the icosahedron.

4) John Baez, Who discovered the icosahedron?, talk at the Special Session on History and Philosophy of Mathematics, 2009 Fall Western Section Meeting of the AMS, November 7, 2009. Available at http://math.ucr.edu/home/baez/icosahedron/
The dodecahedron and icosahedron are the most exotic of the Platonic solids, because they have 5-fold rotational symmetry - a possibility that only exists for regular polytopes in 2, 3 or 4 dimensions. The dodecahedron and icosahedron have the same symmetry group, because they are Poincaré duals: the vertices of one correspond to faces of the other. But the icosahedron was probably discovered later. As Benno Artmann wrote:
The original knowledge of the dodecahedron may have come from crystals of pyrite, but in contrast the icosahedron is a pure mathematical creation.... It is the first realization of an entity that existed before only in abstract thought. (Well, apart from the statues of gods!)
I'm not sure it's really anything close to the first "realization of an entity that existed before only in abstract thought". But it may have been the first "exceptional" object in mathematics - roughtly speaking, an entity that doesn't fit into any easy pattern, which is discovered as part of proving a classification theorem!
Other exceptional objects include the simple Lie group E8, and the finite simple group M12. Intriguingly, many of these exceptional objects" are related. For example, the icosahedron can be used to construct both E8 and M12. But the first interesting classification theorem was the classification of regular polyhedra: convex polyhedra with equilateral polygons as faces, and the same number of faces meeting at each vertex. This theorem appears almost at the end of the last book of Euclid's Elements - Book XIII. It shows that the only possibilities are the Platonic solids: the tetrahedron, the cube, the octahedron, the dodecahedron and the icosahedron. And according to traditional wisdom, the results in this book were proved by Theatetus, who also discovered the icosahedron!
Indeed, Artmann cites an "an ancient note written in the margins of the manuscript" of Book XIII, which says:
In this book, the 13th, are constructed the five so-called Platonic figures which, however, do not belong to Plato, three of the five being due to the Pythagoreans, namely the cube, the pyramid, and the dodecahedron, while the octahedron and the icosahedron are due to Theaetetus.
You may know Theaetetus through Plato's dialog of the same name, where he's described as a mathematical genius. He's also mentioned in Plato's dialogue called the Sophist. In the Republic, written around 380 BC, Plato complained that not enough is known about solid geometry:
... and for two reasons: in the first place, no government places value on it; this leads to a lack of energy in the pursuit of it, and it is difficult. In the second place, students cannot learn it unless they have a teacher. But then a teacher can hardly be found....
Theaetetus seems to have filled the gap: he worked on solid geometry between 380 and 370 BC, perhaps inspired by Plato's interest in the subject. He died from battle wounds and dysentery in 369 after Athens fought a battle with Corinth.
But how certain are we that Theatetus discovered - or at least studied - the icosahedron? The only hard evidence seems to be this "ancient note" in the margins of the Elements. But who wrote it, and when?
First of all, if you hope to see an ancient manuscript by Euclid with a scribbled note in the margin, prepare to be disappointed! All we have are copies of copies of copies. The oldest remaining fragments of the Elements date to centuries after Euclid's death: some from a library in Herculaneum roasted by the eruption of Mount Vesuvius in 79 AD, a couple from the Fayum region near the Nile, and some from a garbage dump in the Egyptian town of Oxyrhynchus.
There are various lines of copies of Euclid's Elements. Comparing these to guess the contents of the original Elements is a difficult and fascinating task. Unfortunately, in the fourth century AD, the Greek mathematician Theon of Alexandria - Hypatia's dad - made a copy that became extremely popular. So popular, in fact, that for many centuries European scholars knew no line of copies that hadn't passed through Theon! And Theon wasn't a faithful copyist: he added extra propositions, lengthened some proofs, and omitted a few things too. It seems he wanted to standardize the language and make it easier to follow. This may have helped people trying to learn geometry - but certainly not scholars trying to understand Euclid.
In 1808, Francois Peyrard made a marvelous discovery. He found that the Vatican library had a copy of Euclid's Elements that hadn't descended through Theon!
This copy is now called "P". It dates back to about 850 AD. I would love to know how Peyrard got his hands on it. One imagines him rooting around in a dusty basement and opening a trunk... but it seems that Napoleon somehow took this manuscript from the Vatican to Paris.
In the 1880s, the great Danish scholar Johan Heiberg used "P" together with various "Theonine" copies of the Elements to prepare what's still considered the definitive Greek edition of this book. The all-important English translation by Thomas Heath is based on this. As far as I can tell, "P" is the only known non-Theonine copy of Euclid except for the fragments I mentioned. Heath also used these fragments to prepare his translation.
This is just a quick overview of a complicated detective story. As always, the fractal texture of history reveals more complexity the more closely you look.
Anyway, Heath thinks that Geminus of Rhodes wrote the "ancient note" in the Elements crediting Theatetus. I'm not sure why Heath thinks this, but Geminus of Rhodes was a Greek astronomer and mathematician who worked during the 1st century BC.
In his charming article "The discovery of the regular solids", William Waterhouse writes:
Once upon a time there was no problem in the history of the regular solids. According to Proclus, the discoveries of Pythagoras include "the construction of the cosmic solids," and early historians could only assume that the subject sprang full-grown from his head. But a better-developed picture of the growth of Greek geometry made such an early date seem questionable, and evidence was uncovered suggesting a different attribution. A thorough study of the testimony was made by E. Sachs, and her conclusion is now generally accepted: the attribution to Pythagoras is a later misunderstanding and/or invention.The history of the regular solids thus rests almost entirely on a scholium to Euclid which reads as follows:
"In this book, the 13th, are constructed the 5 figures called Platonic, which however do not belong to Plato. Three of these 5 figures, the cube, pyramid, and dodecahedron, belong to the Pythagoreans; while the octahedron and icosahedron belong to Theaetetus."
Theaetetus lived c. 415-369 B.C., so this version gives a moderately late date; and it has the considerable advantage of seeming unlikely. That is, the details in the scholium are not the sort of history one would naively conjecture, and hence it is probably not one of the stories invented in late antiquity. As van der Waerden says, the scholium is now widely accepted "precisely because [it] directly contradicts the tradition which used to ascribe to Pythagoras anything that came along."
But probability arguments can cut both ways, and those scholars who hesitate to accept the scholium do so primarily because it seems too unlikely. There have been two main sticking places: first, the earliness of the dodecahedron in comparison with the icosahedron; and second, the surprising lateness of the octahedron. The first objection, however, has been fairly well disposed of. The mineral pyrite (FeS2) crystallizes most often in cubes and almost-regular dodecahedra; it is quite widespread, being the most common sulphide, and outstanding crystals are found at a number of spots in Italy. Moreover it regularly occurs mixed with the sulphide ores, and underlying the oxidized ores, of copper; these deposits have been worked since earliest antiquity. Thus natural dodecahedra were conspicuous, and in fact they did attract attention: artificial dodecahedra have been found in Italy dating from before 500 BC. Icosahedral crystals, in contrast, are much less common. Hence there is no real difficulty in supposing that early Pythagorean geometers in Italy were familiar with dodecahedra but had not yet thought of the icosahedron.
Indeed, while I've heard that iron pyrite forms "pseudoicosahedra":
I've never seen one, while the "pyritohedra" resembling regular dodecahedra are pretty common:
The puzzle of why the octahedron showed up so late seems to have this answer: it was known earlier, but it was no big deal until the concept of regular polyhedron was discovered! As Waterhouse says, the discovery of the octahedron would be like the discovery of the 4rd perfect number. Only the surrounding conceptual framework makes the discovery meaningful.
So far, so good. But maybe the Greeks were not the first to discover the icosahedron! In 2003, the mathematicians Michael Atiyah and Paul Sutcliffe wrote:
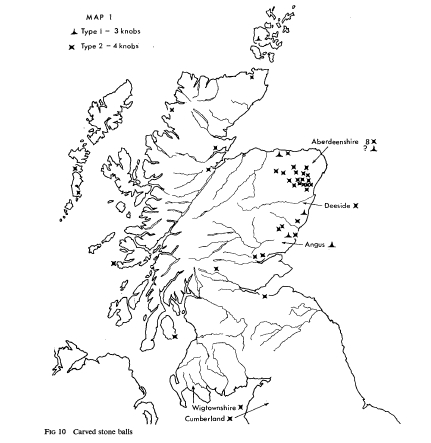
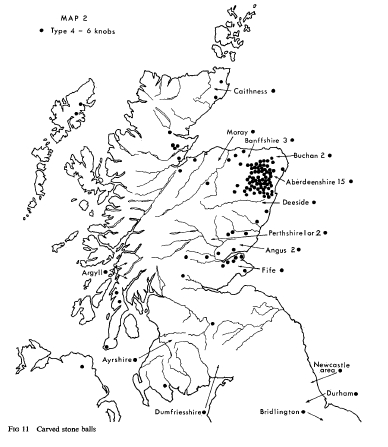
Although they are termed Platonic solids there is convincing evidence that they were known to the Neolithic people of Scotland at least a thousand years before Plato, as demonstrated by the stone models pictured in Fig. 1 which date from this period and are kept in the Ashmolean Museum in Oxford.

Various people including John McKay and myself spread this story without examining it very critically. I did read Dorothy Marshall's excellent paper "Carved stone balls", which catalogues 387 carved stone balls found in Scotland, dating from the Late Neolithic to Early Bronze Age. It has pictures showing a wide variety of interesting geometric patterns carved on them, and maps showing where people have found balls with various numbers of bumps on them. But it doesn't say anything about Platonic solids.
In March of 2009, Lieven le Bruyn posted a skeptical investigation of Atiyah and Sutcliffe's claim. For starters, he looked hard at the photo in their paper:

... where's the icosahedron? The fourth ball sure looks like one but only because someone added ribbons, connecting the centers of the different knobs. If this ribbon-figure is an icosahedron, the ball itself should be another dodecahedron and the ribbons illustrate the fact that icosa- and dodecahedron are dual polyhedra. Similarly for the last ball, if the ribbon-figure is an octahedron, the ball itself should be another cube, having exactly 6 knobs. Who did adorn these artifacts with ribbons, thereby multiplying the number of "found" regular solids by two (the tetrahedron is self-dual)?
Who put on the ribbons? Lieven le Bruyn traced back the photo to Robert Lawlor's 1982 book Sacred Geometry. In this book, Lawlor wrote:
The five regular polyhedra or Platonic solids were known and worked with well before Plato's time. Keith Critchlow in his book Time Stands Still presents convincing evidence that they were known to the Neolithic peoples of Britain at least 1000 years before Plato. This is founded on the existence of a number of spherical stones kept in the Ashmolean Museum at Oxford. Of a size one can carry in the hand, these stones were carved into the precise geometric spherical versions of the cube, tetrahedron, octahedron, icosahedron and dodecahedron, as well as some additional compound and semi-regular solids...
But is this really true? Le Bruyn discovered that the Ashmolean owns only 5 Scottish stone balls - and their webpage shows a photo of them, which looks quite different than the photo in Lawlor's book!
They have no ribbons on them. More importantly, they're different shapes! The Ashmolean lists their 5 balls as having 7, 6, 6, 4 and 14 knobs, respectively - nothing like an icosahedron.
And here is where I did a little research of my own. The library at UC Riverside has a copy of Keith Critchlow's 1979 book Time Stands Still. In this book, we see the same photo of stones with ribbons that appears in Lawlor's book - the photo that Atiyah and Suttcliffe use. In Critchlow's book, these stones are called "a full set of Neolithic 'Platonic solids'". He says they were photographed by one Graham Challifour - but he gives no information as to where they came from!
And Critchlow explicitly denies that the Ashmolean has an icosahedral stone! He writes:
... the author has, during the day, handled five of these remarkable objects in the Ashmolean museum.... I was rapt in admiration as I turned over these remarkable stone objects when another was handed to me which I took to be an icosahedron.... On careful scrutiny, after establishing apparent fivefold symmetry on a number of the axes, a count-up of the projections revealed 14! So it was not an icosahedron.
It seems the myth of Scottish balls shaped like Platonic solids gradually grew with each telling. Could there be any truth to it? Dorothy Marshall records Scottish stone balls with various numbers of knobs, from 3 to 135 - but just two with 20, one at the National Museum in Edinburgh, and one at the Kelvingrove Art Gallery and Museum in Glasgow. Do these look like icosahedra? I'd like to know. But even if they do, should we credit Scots with "discovering the icosahedron"? Perhaps not.
So, it seems the ball is in Theaetetus' court.
Here are some references:
The quote from Benno Artmann appeared in a copy of the AMS Bulletin where the cover illustrates a construction of the icosahedron:
5) Benno Artmann, About the cover: the mathematical conquest of the third dimension, Bulletin of the AMS, 43 (2006), 231-235. Also available at http://www.ams.org/bull/2006-43-02/S0273-0979-06-01111-6/
For more, try this wonderfully entertaining book:
6) Benno Artmann, Euclid - The Creation of Mathematics, Springer, New York, 2nd ed., 2001. (The material on the icosahedron is not in the first edition.)
It's not a scholarly tome: instead, it's a fun and intelligent introduction to Euclid's Elements with lots of interesting digressions. A great book for anyone interested in math!
I should also get ahold of this someday:
7) Benno Artmann, Antike Darstellungen des Ikosaeders, Mitt. DMV 13 (2005), 45-50.
Heath's translation of and commentary on Euclid's Elements is available online thanks to the Perseus Project. The scholium crediting Theatetus for the octahedron and icosahedron is discussed here:
8) Euclid, Elements, trans. Thomas L. Heath, Book XIII, Historical Note, p. 438. Also available at http://old.perseus.tufts.edu/cgi-bin/ptext?doc=Perseus%3Atext%3A1999.01.0086&query=head%3D%23566
while the textual history of the Elements is discussed here:
9) Euclid, Elements, trans. Thomas L. Heath, Chapter 5: The Text, p. 46. Also available at http://old.perseus.tufts.edu/cgi-bin/ptext?lookup=Euc.+5
Anyone interested in Greek mathematics also needs these books by Heath, now available cheap from Dover:
10) Thomas L. Heath, A History of Greek Mathematics. Vol. 1: From Thales to Euclid. Vol. 2: From Aristarchus to Diophantus. Dover Publications, 1981.
The long quote by Waterhouse comes from here:
11) William C. Waterhouse, The discovery of the regular solids, Arch. Hist. Exact Sci. 9 (1972-1973), 212-221.
I haven't yet gotten my hold on this "thorough study" mentioned by Waterhouse - but I will soon:
12) Eva Sachs, Die Fünf Platonischen Körper, zur Geschichte der Mathematik und der Elementenlehre Platons und der Pythagoreer, Berlin, Weidmann, 1917.
I also want to find this discussion of how Peyrard got ahold of the non-Theonine copy of Euclid's Elements:
13) N. M. Swerlow, The Recovery of the exact sciences of antiquity: mathematics, astronomy, geography, in Rome Reborn: The Vatican Library and Renaissance Culture, ed. Grafton, 1993.
Here is Atiyah and Sutcliffe's paper claiming that the Ashmolean has Scottish stone balls shaped like Platonic solids:
14) Michael Atiyah and Paul Sutcliffe, Polyhedra in physics, chemistry and geometry, available as arXiv:math-ph/0303071.
Here is le Bruyn's critical examination of that claim:
15) Lieven le Bruyn, The Scottish solids hoax, March 25, 2009, http://www.neverendingbooks.org/index.php/the-scottish-solids-hoax.html
Here are the books by Critchlow and Lawlor -speculative books from the "sacred geometry" tradition:
16) Keith Critchlow, Time Stands Still, Gordon Fraser, London, 1979.
17) Robert Lawlor, Sacred Geometry: Philosophy and Practice, Thames and Hudson, London, 1982. Available at http://www.scribd.com/doc/13155707/robert-lawlor-sacred-geometry-philosophy-and-practice-1982
Here's the Ashmolean website:
18) British Archaeology at the Ashmolean Museum, Highlights of the British collections: stone balls, http://ashweb2.ashmus.ox.ac.uk/ash/britarch/highlights/stone-balls.html
and here's Dorothy Marshall's paper on stone balls:
19) Dorothy N. Marshall, Carved stone balls, Proc. Soc. Antiq. Scotland, 108 (1976/77), 40-72. Available at http://www.tarbat-discovery.co.uk/Learning%20Files/Carved%20stone%20balls.pdf
Finally, a bit of math.
In the process of researching my talk, I learned a lot about Euclid's Elements, where the construction of the icosahedron - supposedly due to Theaetetus - is described. This construction is Proposition XIII.16, in the final book of the Elements, which is largely about the Platonic solids. This book also has some fascinating results about the golden ratio and polygons with 5-fold symmetry!
The coolest one is Proposition XIII.10. It goes like this.
Take a circle and inscribe a regular pentagon, a regular hexagon, and a regular decagon. Take the edges of these shapes, and use them as the sides of a triangle. Then this is a right triangle!
In other words, if
P
is the side of the pentagon,
H
is the side of the hexagon, and
D
is the side of the decagon, then
P2 = H2 + D2
We can prove this using algebra - but Euclid gave a much cooler proof, which actually find this right triangle hiding inside an icosahedron.
First let's give a completely uninspired algebraic proof.
Start with a unit circle. If we inscribe a regular hexagon in it, then obviously
H = 1
So we just need to compute P and D. If we think of the unit circle as living in the complex plane, then the solutions of
z5 = 1
are the corners of a regular pentagon. So let's solve this equation. We've got
0 = z5 - 1 = (z - 1)(z4 + z3 + z2 + z + 1)
so ignoring the dull solution z = 1, we must solve
z4 + z3 + z2 + z + 1 = 0
This says that the center of mass of the pentagon's corners lies right in the middle of the pentagon.
Now, quartic equations can always be solved using radicals, but it's a lot of work. Luckily, we can solve this one by repeatedly using the quadratic equation! And that's why the Greeks could construct the regular pentagon using a ruler and compass.
The trick is to rewrite our equation like this:
z2 + z + 1 + z-1 + z-2 = 0
and then like this:
(z + z-1)2 + (z + z-1) - 1 = 0
Now it's a quadratic equation in a new variable. So while I said this proof would be uninspired, it did require a tiny glimmer of inspiration. But that's all! Let's write
z + z-1 = x
so our equation becomes
x2 + x - 1 = 0
Solving this, we get two solutions. The one I like is the golden ratio:
x = φ = (-1 + √5)/2 ~ 0.6180339...
Next we need to solve
z + z-1 = φ
This is another quadratic equation:
z2 - φ z + 1 = 0
with two conjugate solutions, one being
z = (φ + (φ2 - 4)½)/2
I've sneakily chosen the solution that's my favorite 5th root of unity:
z = exp(2πi/5) = cos(2π/5) + i sin(2π/5)
So, we're getting
cos(2π/5) = φ/2
A fact we should have learned in high school, but probably never did.
Now we're ready to compute P, the length of the side of a pentagon inscribed in the unit circle:
P2 = |1 - z|2
= (1 - cos(2π/5))2 + (sin(2π/5))2
= 2 - 2 cos(2π/5)
= 2 - φ
Next let's compute D, the length of the side of a decagon inscribed in the unit circle! We can mimic the last stage of the above calculation, but with an angle half as big:
D2 = 2 - 2 cos(π/5)
To go further, we can use a half-angle formula:
cos(π/5) = ((1 + cos(2π/5))/2)½
= (½ + φ/4)½
This gives
D2 = 2 - (2 + φ)½
But we can simplify this a bit more. As any lover of the golden ratio should know,
2 + φ = 2.6180339...
is the square of
1 + φ = 1.6180339...
So we really have
D2 = 1 - φ
Okay. Your eyes have glazed over by now - unless you've secretly been waiting all along for This Week's Finds to cover high-school algebra and trigonometry. But we're done. We see that
P2 = H2 + D2
simply says
2 - φ = 1 + (1 - φ)
That wasn't so bad, but imagine discovering it and proving it using axiomatic geometry back around 300 BC! How did they do it?
For this, let's turn to
20) Ian Mueller, Philosophy of Mathematics and Deductive Structure in Euclid's Elements, MIT Press, Cambridge Massachusetts, 1981.
This is reputed to be be the most thorough investigation of the logical structure of Euclid's Elements! And starting on page 257 he discusses how people could have discovered P2 = H2 + D2 by staring at an icosahedron!
This should not be too surprising. After all, there are pentagons, hexagons and decagons visible in the icosahedron. But I was completely stuck until I cheated and read Mueller's explanation.
If you hold an icosahedron so that one vertex is on top and one is on bottom, you'll see that its vertices are arranged in 4 horizontal layers. From top to bottom, these are:
Pick a vertex from the upper pentagon: call this A. Pick a vertex as close as possible from the lower pentagon: call this B. A is not directly above B. Drop a vertical line down from A until it hits the horizontal plane on which B lies. Call the resulting point C. If you think about this, you'll see that ABC is a right triangle. Greg Egan drew a picture of it:
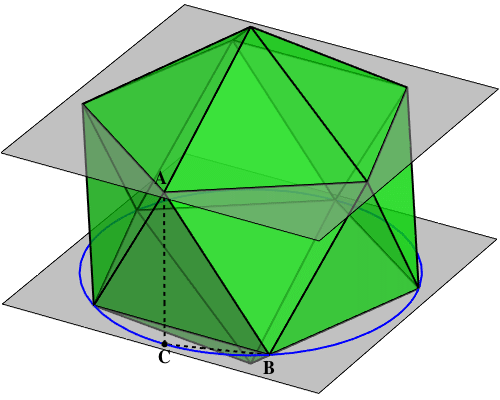
And if we apply the Pythagorean theorem to this triangle we'll get the equation
P2 = H2 + D2
To see this, we only need to check that:
Different circles, but of the same radius! What's this radius? The 5 vertices of the lower pentagon lie on the circle shown in blue. This circle has the right radius.
Using this idea, it's easy to see that the length AB equals the edge of a pentagon inscribed in a circle. It's also easy to see that BC equals the edge of a decagon inscribed in a circle of the same radius. The hard part, at least for me, is seeing that AC equals the edge of a hexagon inscribed in a circle of the same radius... or in other words, the radius of that circle! (The hexagon seems to be a red herring.)
To prove this, it would suffice to show the following marvelous fact: the distance between the "upper pentagon" and the "lower pentagon" equals the radius of the circle containing the vertices of the upper pentagon!
Can you prove this?
In Mueller's book, he suggests various ideas the Greeks could have had about this. Here's one:
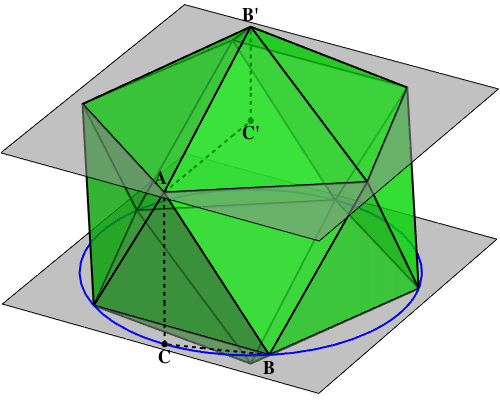
The right triangle ABC is shown here. The trick is to construct another right triangle AB'C'. Here B' is the top vertex, and C' is where a line going straight down from B' hits the plane containing the upper pentagon.
Remember, we're trying to show the distance between the upper pentagon and lower pentagon equals the radius of the circle containing the vertices of the upper pentagon.
But that's equivalent to showing that AC' is congruent to AC.
To do this, it suffices to show that the right triangles ABC and AB'C' are congruent! Can you do it?
In the references to Mueller's book, he says the historians Dijksterhuis (in 1929) and Neuenschwander (in 1975) claimed this is "intuitively evident". But I don't know if that means it's easy to prove!
I thank Toby Bartels and Greg Egan for help with this stuff. I also thank Jim Stasheff for passing on an email from Joe Neisendorfer pointing out Mellinger's picture of the Milky Way.
Addendum: Kevin Buzzard explained some of the Galois theory behind why the pentagon can be constructed with ruler and compass - or in other words, why the quartic
z4 + z3 + z2 + z + 1 = 0
can be solved by solving first one quadratic and then another.
He wrote:
Here ζ5 is number-theorist's jargon for a "primitive 5th root of unity", which in turn is number-theorist's jargon for any 5th root of 1 except for 1 itself.Now, quartic equations can always be solved using radicalsThat's because S4 is a solvable group, and all Galois groups of quartics will live in S4 (and will usually be S4)...Luckily, we can solve this one by repeatedly using the quadratic equation!("this one" being z4 + z3 + z2 + z + 1 = 0.)
...and that's because the Galois group of that specific irreducible polynomial is "only" cyclic of order 4. The splitting field is Q(ζ5), which is a cyclotomic field, so has Galois group (Z/5Z)*. No Z/3Z factors so no messing around with cube roots, for example...
So while I said this proof would be uninspired, it did require a tiny glimmer of inspiration.With this observation above, I'm trying to convince you that the proof really is completely uninspired
To solve the quartic by solving two quadratics, you need to locate the degree 2 subfield of Q(z) (z=ζ5) and aim towards it (because it's your route to the solution). This subfield is clearly the real numbers in Q(z), and the real numbers in Q(z) contains z+z*=z+z-1. So that's sort of a completely conceptual explanation of why the trick works and why it's crucial to introduce z+z-1.
Greg Egan gave a nice modern version of Euclid's original proof of Prop. XIII.10, which states that if you take take a circle and inscribe a regular pentagon, a regular hexagon, and a regular decagon, and make a triangle out of their sides, it's a right triangle!
Here's a version of the proof Euclid gave, adapted from the version JB cited. Rather than proving that various angles here are identical, I've just written in the (easily established) numerical values; there's nothing tricky here, so we might as well take them as given.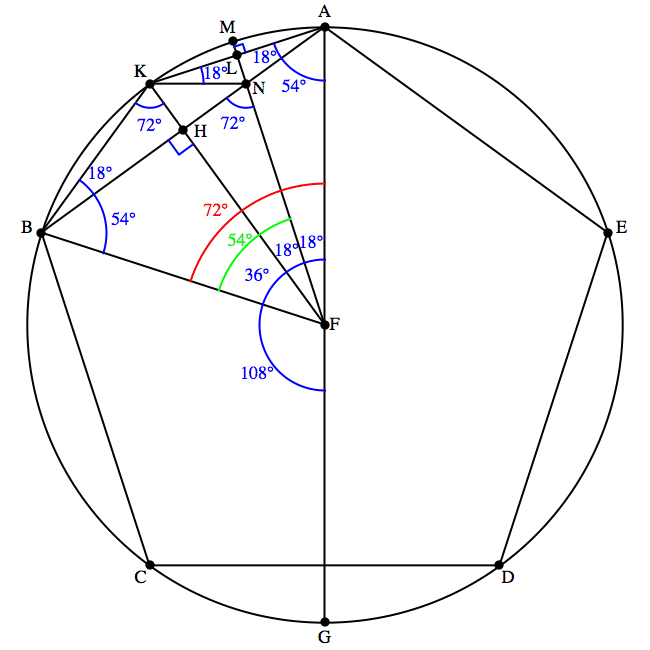
Triangle ABF is similar to triangle BFN. So AB/BF = BF/FN = BF/BN, with the last equality true because the triangles are isosceles with FN = BN. Thus BF 2 = AB · BN
Triangle BAK is similar to triangle KAN. So BA/AK = KA/AN. Thus AK2 = AB · AN.
Adding our two results, we have: BF2 + AK2 = AB · (AN + BN) = AB2.
BF is our radius, AK is a decagon side, and AB is a pentagon side. Well done Euclid.
On Thanksgiving of 2009, I got ahold of Eva Sachs' 1917 book Die Fünf Platonischen Körper, mentioned above. It's supposed to be the authoritative tome on the early history of the Platonic solids.
If anyone out there reads German, I'd love a translation of what she says about the icosahedron and the pentagon-hexagon-decagon identity. Click on the pictures for larger views:
I think the first page gets interesting around "Der Satz XIII 10 lautet..." ("Proposition XIII.10 says...") and more interesting after "Dieser Satz, obwohl planimetrisch, ist durch Betrachtung der ebenen Geometrie nicht leicht zu finden". ("This proposition, though planar in character, is not so easy to find through considerations of plane geometry.")
You'll notice that she focuses our attention on the right triangles ZWQ and QEP, which are the triangles ABC and AB'C' that I mentioned above:

Proving that these are congruent is the key to the pentagon-decagon-hexagon identity!
I'm especially curious about the footnote on page 104, and also the remark further up this page saying "So fand er den Satz XIII 9..." ("This is how he found Proposition XII.9").
To see Greg Egan's beautiful proof of the pentagon-decagon-hexagon identity, which meets my challenge above, see "week284".
For more discussion visit the n-Category Café.
Geometry enlightens the intellect and sets one's mind right. All its proofs are very clear and orderly. It is hardly possible for errors to enter into geometric reasoning, because it is well arranged and orderly. Thus the mind that constantly applies itself to geometry is unlikely to fall into error. - Ibn Khaldun
© 2009 John Baez
baez@math.removethis.ucr.andthis.edu

|
 
|

|