




|
 
|

|
This week we'll start with a math puzzle, then a paper about categorification in analysis. Then we'll continue learning about electrical circuits and their analogues in other branches of physics. We'll wrap up with a bit more rational homotopy theory.
But first: here's an image that's been making the rounds lately. What's going on here?

Next: a math puzzle! This was created by a correspondent who wishes to remain anonymous. Here are some numbers. Each one is the number of elements in some famous mathematical gadget. What are these numbers - and more importantly, what are these gadgets?
The answers are at the end.
The wave of categorification overtaking mathematics is finally hitting analysis! I spoke a tiny bit about this in "week274", right after I'd finished a paper with Baratin, Freidel and Wise on infinite-dimensional representations of 2-groups. I thought it would take a long time for more people to get interested in the blend of 2-categories and measure theory that we were exploring. After all, there's a common stereotype that says mathematicians who like categories hate analysis, and vice versa. But I was wrong:
1) Goncalo Rodrigues, Categorifying measure theory: a roadmap, available as arXiv:0912.4914.
Read both papers together and you'll get a sense of how much there is to do in this area! A lot of basic definitions remain up for grabs. For example, Rodrigues' paper defines "2-Banach spaces", but will his definition catch on? It's too soon to tell. There are already lots of theorems. And there's no shortage of interesting examples and applications to guide us. But finding the best framework will take a while. I urge anyone who likes analysis and category theory to jump into this game while it's still fresh.
But my own work is taking me towards mathematics of a more applied sort. My excuse is that I'll be spending a year in Singapore at the Centre for Quantum Technologies, starting in July. This will give me a chance to think about computation, and condensed matter physics, and quantum information processing, and diagrams for physical systems built from pieces. Such systems range from the humble electrical circuits that I built as a kid, to integrated circuits, to fancy quantum versions of these things.
So, lately I've been talking about a set of analogies relating various types of physical systems. I listed 6 cases where the analogies are quite precise:
displacement flow momentum effort
q dq/dt p dp/dt
Mechanics position velocity momentum force
(translation)
Mechanics angle angular angular torque
(rotation) velocity momentum
Electronics charge current flux voltage
linkage
Hydraulics volume flow pressure pressure
momentum
Thermodynamics entropy entropy temperature temperature
flow momentum
Chemistry moles molar chemical chemical
flow momentum potential
This week I'd like to talk about five circuit elements that we can use
to build more complicated electrical circuits: resistors, inductors,
capacitors, voltage sources, and current sources. I'll tell you the
basic equations they obey, and say a bit about their analogues in the
mechanics of systems with translational degrees of freedom. They also
have analogues in the other rows.
Engineers call these five circuit elements "1-ports". A 1-port can be visualized as a black box with 2 places where you can stick in a wire:
|
|
-----
| |
| |
-----
|
|
More generally, an "n-port" has 2n places where you can
attach a wire. This numbering system may seem peculiar. Indeed, it
overlooks circuits that have an odd number of wires coming out, like
this one made of just wires:
\ /
\ /
\ /
|
|
|
You can use gizmos like this to stick together 1-ports
"in parallel":
|
|
|
/ \
/ \
/ \
--- ---
| | | |
--- ---
\ /
\ /
\ /
|
|
|
However, if you've ever looked at the back of a TV or stereo, you'll
see that place where you can plug in cables tend to come in pairs!
Each pair is called a "port". So, electrical engineers
often - though not always - focus on n-ports, where the wires coming
out are grouped in pairs. And there's probably even a good
mathematical reason for paying special attention to these -
something related to symplectic geometry. That's one of the things
I'm trying to understand better.
Later I'll tell you about some famous 2-ports and 3-ports, but today let's do 1-ports. If we have a 1-port with wires coming out of it, we can arbitrarily choose one wire and call it the the "input", with the other being the "output":
|
V
|
-----
| |
| |
-----
|
V
|
If you know a little category theory, this should seem suspiciously
similar to a "morphism". And if you know a bit more, this
should remind you of other situations where it takes an arbitrary
choice to distinguish between the "input" and the
"output" of a morphism.
Any 1-port has a "flow through it" and an "effort across it", which which are functions of time. Remember, "flow" is the general concept that reduces to current in the special case of electronics. "Effort" is the concept that reduces to voltage.
The time integral of flow is called the "displacement" and denoted q, and the time integral of effort is called the "momentum" and denoted p. So, flow is q' = dq/dt and effort is p' = dp/dt.
To mathematically specify a 1-port, we give one equation involving p, q, p', q', and the time variable t. Here's how it works for the five most popular types of 1-ports:

In all cases, the effort is some function of the flow:
p' = f(q')
An easy special case is a linear resistance, for which the effort is proportional to the flow:
p' = R q'
Here R is some constant, also called the "resistance". In electric circuit theory this equation is called Ohm's law, and people write it using different symbols. Note we need to be careful about our sign conventions: in mechanics we usually think of friction as giving force = R velocity with R negative, while in electric circuit theory we usually think of an ordinary resistor as giving voltage = R current with R positive. The two cases are not fundamentally different: it's just an artifact of differing sign conventions!

In all cases, the displacement is some function of effort:
q = f(p')
An easy special case is a linear capacitance, for which the displacement is proportional to the effort:
q = C p'
Here C is some constant, also called the "capacitance". Again we need to be careful with our conventions: in mechanics we usually think of a spring as being stretched by an amount equal to 1/k times the force applied. Here k, the reciprocal of C, is called the spring constant. But some engineers work with C and call it the "compliance" of the spring. An easily stretched spring has big C, small k.
In all cases, the momentum is some function of flow:
p = f(q')
An easy special case is a linear inertance, for which the momentum is proportional to the flow:
p = L q'
Here L is some constant, also called the "inertance". In the case of mechanics, this would be the mass.

Here the equation is of different type than before! It can involve the time variable t:
p' = f(t)
Here the equation is
q' = f(t)
The voltage and current sources form a family, since only these involve the variable t in an explicit way. Also, only these can be used to add energy to a circuit. So, these two are called "active" circuit elements.
The other three are called "passive". Among these, the capacitance and inertance form a family because they both conserve energy. The resistance is different: it dissipates energy - or more precisely, turns it into heat energy, which is not part of our simple model. If you're more used to mechanics than electrical circuits, let me translate what I'm saying into the language of mechanics: a machine made out of masses and springs will conserve energy, but friction dissipates energy.
Let's try to make this "energy conservation" idea a bit more precise. I've already said that p'q', effort times flow, has dimensions of power - that is, energy per time. Indeed, for any 1-port, the physical meaning of p'q' is the rate at which energy is being put in. So, in electrical circuit theory, people sometimes say energy is "conserved" if we can find some function H(p,q) with the property that
dH(p,q)/dt = p'q'
This function H, called the "Hamiltonian", describes the energy stored in the 1-port. And this equation says that the energy stored in the system changes at a rate equal to the rate at which energy is put in! So energy doesn't get lost, or appear out of nowhere.
Now, when I said "energy conservation", you may have been expecting something like dH/dt = 0. But we only get that kind of energy conservation for "closed" systems - systems that aren't interacting with the outside world. We'll indeed get dH/dt = 0 when we build a big circuit with no inputs and no outputs out of circuit elements that conserve energy in the above sense. The energy of the overall system will be conserved, but of course it can flow in and out of the various parts.
But of course it's really important to think about circuits with inputs and outputs - the kind of gizmo you actually plug into the wall, or hook up to other gizmos! So we need to generalize classical mechanics to "open" systems: systems that can interact with their environment. This will let us study how big systems are made of parts.
But right now we're just studying the building blocks - and only the simplest ones, the 1-ports.
Let's see how energy conservation works for all five 1-ports. For simplicity I'll only do the linear 1-ports when those are available, but the results generalize to the nonlinear case:
p' = R q'
so the power is
p'q' = R (q')2
In the physically realistic case R > 0 so this is nonnegative, meaning that we can only put energy into the resistor. And note that p'q' is not the time derivative of some function of p and q, so energy is not conserved. We say the resistance "dissipates" energy.
q = C p'
so the power is
p'q' = qq' / C
Note that unlike the resistor this can take either sign, even in the physically realistic case C > 0. More importantly, in this case p'q' is the time derivative of a function of p and q, namely
H(p,q) = q2 / 2C
So in this case energy is conserved. If you're comfortable with mechanics you'll remember that a spring is an example of a capacitance, and H(p,q) is the usual "potential energy" of a spring when C is the reciprocal of the spring constant.
p = L q'
so the power is
p'q' = pp' / L
Again this can take either sign, even in the physically realistic case L > 0. And again, p'q' is the time derivative of a function of p and q, namely
H(p,q) = p2 / 2L
So energy is also conserved in this case. If you're comfortable with mechanics you'll remember that a mass is an example of a inertance, and H(p,q) is the usual "kinetic energy" of a mass when L equals the mass.
p' = f(t)
for some function f, so the power is
p'q' = f(t) q'
This is typically not the time derivative of some function of p and q, so energy is not usually conserved. I leave it as a puzzle to give the correct explanation of what's going on when f(t) is a constant.
q' = f(t)
for some function f, so the power is
p'q' = f(t) p'
This is typically not the time derivative of some function of p and q, so energy is not usually conserved. Again, I leave it as a puzzle to understand what's going on when f(t) is constant.
So, everything works as promised. But if your background in classical mechanics is anything like mine, you should still be puzzled by the equation
dH(p,q)/dt = p'q'
This is sometimes called the "power balance equation". But you mainly see it in books on electrical engineering, not classical mechanics. And I think there's a reason. I don't see how to derive it from a general formalism for classical mechanics, the way I can derive dH/dt = 0 in Hamiltonian mechanics. At least, I don't see how when we write the equation this way. I think we need to write it a bit differently!
In fact, I was quite confused until Tim van Beek pointed me to a nice discussion of this issue here:
2) Bernard Brogliato, Rogelio Lozano, Bernhard Maschke and Olav Egeland, Dissipative Systems Analysis and Control: Theory and Applications, 2nd edition, Springer, Berlin, 2007.
I'll say more about this later. For now let me just explain two buzzwords here: "control theory" and "dissipative systems".
Traditional physics books focus on closed systems. "Control theory" is the branch of physics that focuses on open systems - and how to make them do what you want!
For example, suppose you want to balance a pole on your finger. How should you move your finger to keep the pole from falling over? That's a control theory problem. You probably don't need to read a book to solve this particular problem: we're pretty good at learning to do tricks like this without thinking about math. But if you wanted to build a robot that could do this - or do just about anything - control theory might help.
What about "dissipative systems"? I already gave an example: a circuit containing a resistor. I talked about another in "week288": a mass on a spring with friction. In general, a dissipative system is one that loses energy, or more precisely converts it to heat. We often don't want to model the molecular wiggling that describes heat. If we leave this out, dissipative systems are not covered by ordinary Hamiltonian mechanics - since that framework has energy conservation built in. But there are generalizations of Hamiltonian mechanics that include dissipation! And these are pretty important in practical subjects like control theory... since life is full of friction, as you've probably noticed.
So, this book covers everything that my classical mechanics education downplayed or left out: open systems, dissipation and control theory! And in the chapter on "dissipative physical systems", it derives power balance equations for "input-output Hamiltonian systems" and "port-controlled Hamiltonian systems". Apparently it's the latter that describes physical systems built from n-ports.
For more on port-controlled Hamiltonian systems, this book recommends:
3) B. M. Maschke and A. J. van der Schaft, Port controlled Hamiltonian systems: modeling origins and system theoretic properties, in Proceedings of the 2nd IFAC Symp. on Nonlinear Control Systems Design, NOLCOS'92 (1992), pp. 282-288,
4) B. M. Maschke and A. J. van der Schaft, The Hamiltonian formulation of energy conserving physical systems with ports, Archiv fur Elektronik und Ubertragungstechnik 49 (1995), 362-371.
5) A. J. van der Schaft, L2-gain and Passivity Techniques in Nonlinear Control, 2nd edition, Springer, Berlin, 2000.
So, I need I learn more about this stuff, and then explain it to you. But let's stop here for now, and turn to... rational homotopy theory!
Nothing big this week: I just want to take stock of where we are. I've been trying to explain a triangle of concepts:
RATIONAL SPACES
/ \
/ \
/ \
/ \
/ \
DIFFERENTIAL GRADED ------- DIFFERENTIAL GRADED
COMMUTATIVE ALGEBRAS LIE ALGEBRAS
In "week287" I explained a functor going down the left side of this triangle. In fact I explained how we can get a differential graded commutative algebra, or DGCA, from any topological space. This involved a grand generalization of differential forms.
In "week289" I explained a functor going down the right side. In fact I explained how we can get a differential graded Lie algebra, or DGLA, from any topological space with a chosen basepoint. This involved a grand generalization of Lie groups, and their Lie algebras.
Today I'd like to explain a sense in which all three concepts in this triangle are "the same". I won't give you the best possible theorem along these lines - just Quillen's original result, which is pretty easy to understand. It says that three categories are equivalent: one for each corner of our triangle!
I explained the first category back in "week286". I called it the "rational homotopy category", and I described it in several ways. Here's one. Start with the category where:
f: X → X'
that give isomorphisms between rational homotopy groups:
Q ⊗ πn(f): Q ⊗ πn(X) → Q ⊗ πn(X')
This gives the rational homotopy category.
The second category involves DGCAs. Well - actually not. To get the nicest results, it seems we should work dually and use differential graded cocommutative coalgebras, or DGCCs. I'm sorry to switch gears on you like this, but that's life. The difference is "purely technical", but I want to state a theorem that I'm sure is true!
In "week287" we saw how Sullivan took any space and built a DGCA whose cohomology was the rational cohomology of that space. But today let's follow Quillen and instead work with a DGCC whose homology is the rational homology of our space.
So, let's start with the category of DGCC's over the rational numbers - but not all of them, only those that are trivial in the bottom two dimensions:
d d d d
0 <--- 0 <--- C2 <--- C3 <--- ...
Why? Because our spaces are 1-connected, so their bottom two
homology groups are boring. Then, let's throw in formal inverses to
"quasi-isomorphisms" - that is, maps between DGCCs
f: C → C'
that give isomorphisms between homology groups:
Hn(f): Hn(C) → Hn(C')
The resulting category is equivalent to the rational homotopy category!
The third category involves DGLAs. We start with the category of DGLAs over the rational numbers - but not all of them, only those that are trivial in the bottom dimension:
d d d d
0 <--- L1 <--- L2 <--- L3 <--- ...
Just the very bottom dimension, not the bottom two! Why? Because we
get a DGLA from the group of loops in our rational space, and
looping pushes down dimensions by one. Then, we throw in formal
inverses to "quasi-isomorphisms" - that is, maps between
DGLAs:
f: L → L'
that give isomorphisms between homology groups:
Hn(f): Hn(L) → Hn(L')
Again, the resulting category is equivalent to the rational homotopy category!
So, we have a nice unified picture. We could certainly improve it in various ways. For example, I haven't discussed the bottom edge of the triangle. Doing this quickly brings in L∞-algebras, which are like DGLAs where all the laws hold only "up to chain homotopy". It also brings in gadgets that are like DGCAs or DGCCs, but where all the laws hold only up to chain homotopy. This outlook eventually leads us to realize that we have something much better than three equivalent categories. We have three equivalent (∞,1)-categories!
But there's also the question of what we can do with this triangle of concepts. There are lots of classic applications to topology, and lots of new applications to mathematical physics.
So, there's more to come.
As for the number puzzle at the beginning, all the numbers I listed are the sizes of various "finite simple groups". These are the building blocks from which all finite groups can be built. You can see a list of them here:
6) Wikipedia, Finite simple groups, http://en.wikipedia.org/wiki/List_of_finite_simple_groups
There are 16 infinite families and 26 exceptions, called "sporadic" finite simple groups. Anyway, here we go:
60, which is the number of elements in the smallest nonabelian finite simple group, namely A5. Here An is an an "alternating group": the group of even permutations of the set with n elements. By some wonderful freak of nature, A5 is isomorphic to both PSL(2,4) and PSL(2,5). Here PSL(n,q) is a "projective special linear group": the group of determinant-1 linear transformations of an n-dimensional vector space over the field with q elements, modulo its center.
168, which is the number of elements - or "order" - of the second smallest nonabelian finite simple group, namely PSL(2,7). Thanks to another marvelous coincidence, this is isomorphic to PSL(3,2). See "week214" for a lot more about this group and its relation to Klein's quartic curve and the Fano plane.
504, which is the order of the finite simple group PSL(2,8).
7,920, which is the order of the finite simple group M11 - the smallest of the finite simple groups called Mathieu groups. See "week234" for more about this.
How many minutes are in 2 weeks?
20,160, which is the order of the finite simple group A8. Thanks to another marvelous coincidence, this is isomorphic to PSL(4,2). And there's also another nonisomorphic finite simple group of the same size, namely PSL(3,4)!
How many inches are in 1.5 miles?
95,040, which is the order of the finite simple group M12 - the second smallest of the Mathieu groups. See "week234" for more about this one, too.
How many seconds are in a week?
604,800, which is the order of the finite simple group J2 - the second Janko group, also called the Hall-Janko group. I don't know anything about the Janko groups. They don't seem to have much in common except being sporadic finite simple groups that were discovered by Janko.
I like what the Wikipedia says about the third Janko group: it "seems unrelated to any other sporadic groups (or to anything else)". Unrelated to anything else? Zounds!
How many seconds are in 3 weeks?
1,814,400, which is the order of the finite simple group A10.
7) John Baez, Why there are 63360 inches in a mile?, http://math.ucr.edu/home/baez/inches.html
It's a curious number:
63360 = 27 × 32 × 5 × 11
It seems rather odd that this number is divisible by 11. Find out why it is!
Finally, what about that image? Unsurprisingly, it's from Mars. It shows a dune field less than 400 kilometers from the north pole, bordered on both sides by flat regions - but also a big cliff on one side:
8) HiRISE (High Resolution Imaging Science Experiments), Falling material kicks up cloud of dust on dunes, http://hirise.lpl.arizona.edu/PSP_007962_2635
Some streaks on the dunes look like stands of trees lined up on hilltops:
It would be great if there were trees on Mars, but it's not true. In fact what you're seeing are steep slopes with dark stuff slowly sliding down them! Here's a description written by Candy Hansen, a member of NASA's Mars Reconnaissance Orbiter team at the University of Arizona:
There is a vast region of sand dunes at high northern latitudes on Mars. In the winter, a layer of carbon dioxide ice covers the dunes, and in the spring as the sun warms the ice it evaporates. This is a very active process, and sand dislodged from the crests of the dunes cascades down, forming dark streaks.
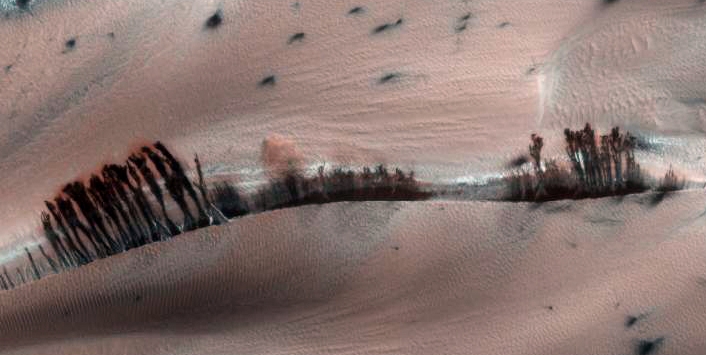
In the subimage falling material has kicked up a small cloud of dust. The color of the ice surrounding adjacent streaks of material suggests that dust has settled on the ice at the bottom after similar events.
Also discernible in this subimage are polygonal cracks in the ice on the dunes (the cracks disappear when the ice is gone).
Addenda: I thank Toby Bartels, Bruce Smith, and Don Davis of Boston for some corrections.
In particular, the number of inches in a mile is divisible by 11 because there are 33/2 feet in a rod. For the explanation of that, see my webpage. But Don Davis pointed out that this is not the only reason why the number 11 appears in the American system of units. A US liquid gallon is 231 = 3 × 7 × 11 cubic inches!
Why? According to Don Davis and the Wikipedia article on gallons) the reason is that once upon a time, a British wine gallon was 7 inches across and 6 inches deep - for some untold reason that deserves further investigation. If we approximate π by 22/7, the volume then comes out to 3 × 7 × 11 cubic inches!
This 11-ness of the gallon then infects other units of volume. For example, a US liquid ounce is
3 × 7 × 11 / 27
cubic inches!
My friend Bruce Smith says that his young son Peter offered the following correction to the quote of the week: it should really be "The most important thing is to keep the 2nd most important thing the 2nd most important thing" - because the first most important thing is the topic of the sentence!
John McKay writes:
You say you don't know anything about the Janko groups. Let me help you...The first Janko group is a subgroup of G2(11). It is called J1 and has order = 11 × (11+1) × (113-1) suggesting incorrectly it may be one of a family. This is the first of the modern sporadics. Then came J2 and J3 both having isomorphic involution centralizers. The first was constructed by Marshall Hall and the second by Graham Higman and me.
David Wales and I decided on the names so that Jk has a Schur multiplier (=second cohomology group) of order k. J2 is the Hall-Janko group. Janko finally produced his fourth group J4 (which unfortunately does not have a Schur multiplier of order 4)! J1,J3, and J4 are among the Pariahs (as are O'Nan, Rud, Ly-Sims). They are those sporadics that have no involvement with M = the Monster group (see Mark Ronan's book).
This group, M, appears to have incredible connections with many areas of mathematics and of physics. Its real nature has yet to be revealed.
Best,
John
Here G2(11) is like the exceptional Lie group G2 except it's defined over the field with 11 elements. So, the number 11 raises its ugly head yet again!
For more discussion, visit the n-Category Café.
The most important thing is to keep the most important thing the most important thing. - Donald P. Coduto
© 2010 John Baez
baez@math.removethis.ucr.andthis.edu

|
 
|

|