
Page last updated 30 April 2020
Here’s a mildly accessible research statement for non-experts that I wrote for a fellowship application recently. Below is some background to my research. I’ve provided proofs to some of the theorems in the first two sections, but I didn’t write up any scaffolding for those proofs and so they may be much hairier than the rest of the exposition.
Let $G$ be a finite abelian $p$-group for a prime $p$. Then $G$ decomposes into a finite sum of cyclic $p$-groups \begin{equation*} G \;\cong\; \frac{\mathbf{Z}}{\left(p^{\lambda_1}\right)} \oplus \dotsb \oplus \frac{\mathbf{Z}}{\left(p^{\lambda_r}\right)} \,. \end{equation*}
As a convenience we’ll say $\lambda_1 \geq \dotsb \geq \lambda_r$. Define the length of $G$ to be $\ell(G) := \sum_{i=0}^r \lambda_i$, so we can think of $\lambda = (\lambda_1, \dotsc, \lambda_r)$ as a partition of the integer $\ell(G).$ We’ll refer to the partition $\lambda$ as the type of $G,$ noting that $G$ is uniquely determined by $p$ and $\lambda$. Let $g_{\mu\nu}^\lambda(p)$ denote the number of normal subgroups $N \mathrel{\triangleleft} G$ of type $\nu$ such that $G/N$ has type $\mu$. In this context $\mu$ is referred to as the cotype of $\nu$.
The function $g_{\mu \nu}^\lambda \colon \text{Primes} \to \mathbf{Z}$ is a polynomial function. That is, letting $q$ be an indeterminate, $g_{\mu \nu}^\lambda(q) \in \mathbf{Z}[q]$. This is called the Hall polynomial associated to the triple $(\nu,\lambda,\mu)$.
The functions between finite abelian $p$-groups for a fixed $p$ depends entirely on the elementary divisors of the groups. That is, the functions depend only on the partition of $\mathrm{\ell}(G)$, and the specific prime $p$ is just a parameter. The clever idea here is that we can use these Hall polynomials as the structure constants of an algebra that encapsulates all the data of the relationship between $p$-groups depending on their type. For an indeterminate $q$, let $\mathbf{H}$ be the $\mathbf{Z}[q]$-module with a basis consisting of formal symbols $u_\lambda$, each corresponding to a partition $\lambda$. We define an algebra structure on this module via the multiplication
\begin{equation*} u_\mu u_\nu \;:=\; \sum_\lambda g_{\mu \nu}^\lambda(q) u_\lambda \,. \end{equation*}
This $\mathbf{H}$ is a commutative associative unital algebra, called the Hall algebra.
The unital bit is easy: the identity element $u_\emptyset$ of $\mathbf{H}$
corresponds to the only partition $\emptyset$ on $0$ letters.
The associative bit is just a tad more involved,
and I’ll save this for a more general version of this theorem to come later.
The facts behind $\mathbf{H}$ being commutative come from the
character theory of abelian groups,
or more generally from
Matlis duality
if you look at Macdonald’s Symmetric Functions and Hall Polynomials.
Duality if key to proof, but it can be
proven more easily
in this simple case.
Recall that $\mathbf{Q}/\mathbf{Z}$ is an injective abelian group (because it’s divisible).
Consider the contravariant functor that sends a group $G$ to $\mathrm{Hom}\left(G, \mathbf{Q}/\mathbf{Z}\right)$,
Let $G$ be an elementary $p$-group of the form $\mathbf{Z}/(p^n)$ for some positive integer $n$,
and note that $\mathbf{Z}/(p^n) \cong \mathrm{Hom}\left(\mathbf{Z}/(p^n), \mathbf{Q}/\mathbf{Z}\right)$.
This functor is exact since $\mathbf{Q}/\mathbf{Z}$ is injective,
so applying it to an exact sequence $N \hookrightarrow G ↠ G/N$,
where $N$ is also an elementary $p$-group, gives a bijective correspondence between
exact sequences of that form and exact sequences $N ↞ G ↩ G/N$.
Then the functor $\mathrm{Hom}\left({-}, \mathbf{Q}/\mathbf{Z}\right)$ is additive,
extending this idea to all such finite abelian $p$-groups,
giving us the commutativity $g_{\mu\nu}^\lambda = g_{\nu\mu}^\lambda$ that we want.
This is basically Ernst Steinitz’s original construction from about a century ago in Zur Theorie der Abelschen Gruppen. In 1959, Philip Hall in The Algebra of Partitions revitalized this construction in greater generality, noting that the fact we’re talking about $p$-groups is incidental, and really the structure of $\mathbf{H}$ is about integer partitions, relating $\mathbf{H}$ to the theory of nilpotent matrices, and to symmetric functions and representations of $S_n$. This construction is very early example of categorification, where we view an algebraic object simply as a shadow of a category, usually related someway to the Grothendieck group. In this last example we are taking the opposite perspective though, decategorification, where be build a single algebraic object that encapsulates all the data, or at least the bits of data that are important, of a particular category that we want to study. The above example can be thought of as a decategorification of the category of finite-length modules over $\mathbf{Z}_p$, the ring of $p$-adic integers. And this decategorification can readily be generalized to get an algebraic structure from any category of finite-length modules over a discrete valuation ring, as described in Macdonald’s book Symmetric Functions and Hall Polynomials.
While (de)categorification can, at the very least, allow us to look at a problem from the perspective of either category theory or algebra, it can often indicate to us a deeper connection between mathematical objects that are not obviously related. In a series of papers published in the early 90s Claus Michael Ringel illustrated such a connection relating the category of quiver representations to symmetrisable Kac-Moody Lie algebras. We’ll briefly describe this relationships, but first we’ll first need a more general definition of Hall algebra. Both Olivier Schiffmann’s notes and Andrew Hubery’s notes are good references on the Ringel-Hall algebras (sometimes just called Hall algebras), to be defined now.
Let $\boldsymbol{k}$ be a finite field. For an essentially small, exact, $\boldsymbol{k}$-linear category $\mathcal{C}$, let $\mathrm{Iso}\mathcal{C}$ denote the set of isomorphism classes of objects in $\mathcal{C}$. We’ll say that such a category is finitary if for any objects $A$ and $B$, both $\dim\mathrm{Hom}_\boldsymbol{k}(A,B)$ and $\dim\mathrm{Ext}^1_\boldsymbol{k}(A,B)$ are finite, and we’ll say it’s hereditary if $\mathrm{Ext}^i(A,B) = 0$ for $i>1$. Let $E_{A\,B}^X$ denote the set of short exact sequences $B \hookrightarrow X ↠ A$ in $\mathcal{C}$.
Let $v = q^2$ be indeterminates. The Ringel-Hall algebra $\mathbf{H}_\mathcal{C}$ of $\mathcal{C}$ has as its underlying module the free $\mathbf{Z}[q]$-module generated by $\mathrm{Iso}\mathcal{C}$. For two isomorphism classes $[A]$ and $[B]$, we want their product in $\mathbf{H}_\mathcal{C}$ to encapsulate the data of “distinct” short exact sequence in $\mathcal{C}$ of the form $B \hookrightarrow {-} ↠ A$. For an object $X$ let’s define the Hall number $F_{A\,B}^X$ as \begin{equation*} F_{A\,B}^X = \frac{\left|E_{A\,B}^X\right|}{|\mathrm{Aut}_\mathcal{C}(A)|\times|\mathrm{Aut}_\mathcal{C}(B)|} \,. \end{equation*} By dividing by $|\mathrm{Aut}_\mathcal{C}(A)|\times|\mathrm{Aut}_\mathcal{C}(B)|$ we are, instead of just counting the short exact sequences $B \hookrightarrow X ↠ A$, counting distinct ways that $B$ can be a subobject of $X$ such that $\mathrm{Coker}(B \hookrightarrow X) = A$. Then we define a $\mathbf{Z}$-linear multiplication $\cdot$ in $\mathbf{H}_\mathcal{C}$ as \begin{equation*} [A]\cdot[B] = \sum_{[X] \in \mathrm{Iso}\mathcal{C}} F_{A\,B}^X [X] \,. \end{equation*}
This $\mathbf{H}_\mathcal{C}$ is an associative $\mathbf{Z}[q]$-algebra.
To be more terse we’ll write $A$ for the isomorphism class $[A]$ that contains $A$, and we’ll basically follow the proof in Hubery’s notes. Writing out $\left(A\cdot (B \cdot C)\right)$ and $\left((A \cdot B)\cdot C \right)$, we arrive at \begin{equation*} A\cdot (B \cdot C) = \sum_{X}\sum_{Y} F_{B\,C}^{Y}F_{A\,Y}^X X \qquad (A \cdot B)\cdot C = \sum_{X}\sum_{Y'} F_{A\,B}^{Y'}F_{Y'\,C}^X X \,. \end{equation*}
Writing the Hall numbers in terms of $E_{A\,B}^X$ again, we can show these are equal by showing that for any fixed object $X$ we have \begin{equation*} \sum_{Y} \frac{E_{B\,C}^{Y}E_{A\,Y}^X}{\mathrm{Aut}_{\mathcal{C}}(Y)} \;\;=\;\; \sum_{Y'} \frac{E_{A\,B}^{Y'}E_{Y'\,C}^X}{\mathrm{Aut}_{\mathcal{C}}(Y')} \,. \end{equation*}
The key idea here is that the left sum is counting the number of filtrations of $X$,
distinct up to an automorphism of $Y$,
with quotients isomorphic to $A$, $B$, and $C$ in that order,
while the right sum is counting the number of cofiltrations of $X$,
distinct up to an automorphism of $Y'$,
with kernels isomorphic to $A$, $B$, and $C$ in that order.
The two diagrams that this suggests are:
 Then we can establish a bijection between these sets
of filtrations (left) and cofiltrations (right) to get the equality above.
Starting with the filtration, let $Y'$ be the pushout
of the span $B ↞ Y \hookrightarrow X$.
Then we can establish a bijection between these sets
of filtrations (left) and cofiltrations (right) to get the equality above.
Starting with the filtration, let $Y'$ be the pushout
of the span $B ↞ Y \hookrightarrow X$.
By the universal property of the pushout,
since the map $Y ↠ B$ is epic
the induced map $X \to Y'$ will be epic too.
Considering the map $X ↠ A$ and the zero map $B \to A$,
the pushout also gives us a map $Y' \to A$ that’ll be epic
since $X ↠ Y' \to A \;=\; X ↠ A$,
such that the kernel of $Y' \to A$ is $B$.
And similarly $C$ will be the kernel of the map $X \to Y'$.
This gives us the diagram:
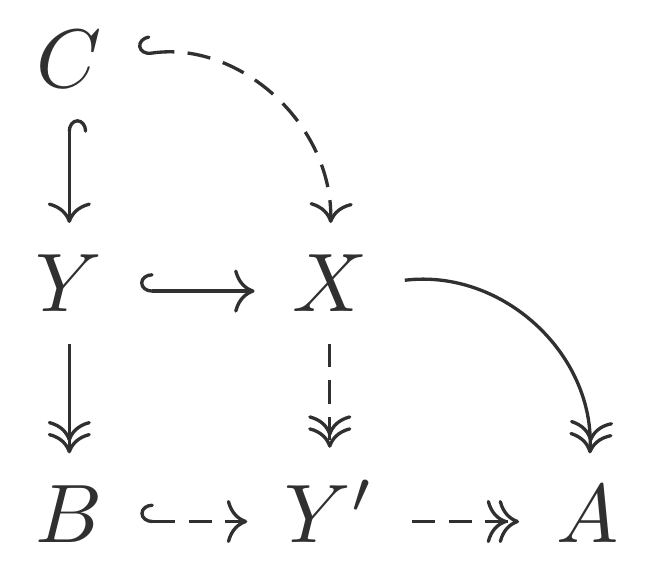 And we can similarly take the pullback of a cospan $B \hookrightarrow Y' ↞ X$
to work out the other direction of the bijective correspondence.
And we can similarly take the pullback of a cospan $B \hookrightarrow Y' ↞ X$
to work out the other direction of the bijective correspondence.
The Hall algebra isn’t necessarily commutative like in the case of $p$-groups, and is only unital if your category has a zero object. Now we want to define this Hall algebra more generally still, as a free $\mathbf{Z}\left[v,v^{-1}\right]$-module with a little “twist” in the multiplication. Define the Euler form in $\mathcal{C}$ as \begin{equation*} \newcommand{\innerproduct}[2]{\left\langle#1 , #2\right\rangle} \innerproduct{A}{B} := \dim\mathrm{Hom}_\boldsymbol{k}(A,B) - \dim\mathrm{Ext}^1_\boldsymbol{k}(A,B) \,. \end{equation*} Remembering $q=v^2$ are indeterminates, as Ringel does in The Hall Algebra Approach to Quantum Groups define the twisted Ringel-Hall algebra $\mathbf{H}_\mathcal{C}^\ast$ as \begin{equation*} \mathbf{H}_\mathcal{C}^\ast := \mathbf{Z}\left[v, v^{-1}\right] \otimes_{\mathbf{Z}[q]} \mathbf{H}_\mathcal{C} \,, \end{equation*} and we define a multiplication $\mathrm{\nabla}$ on $\mathbf{H}_\mathcal{C}^\ast$ given by \begin{equation*} \mathrm{\nabla}\big([A],[B]\big) = % [A][B] = % v^{\innerproduct{A}{B}} [A]\cdot[B] = % \sum_{[X] \in \mathrm{Iso}\mathcal{C}} v^{\innerproduct{A}{B}} F_{A\,B}^X [X] \,. \end{equation*}
This twisted multiplication gives $\mathbf{H}_\mathcal{C}^\ast$ the structure of an associative $\mathbf{Z}\left[v, v^{-1}\right]$-algebra, and furthermore $\mathbf{H}_\mathcal{C}^\ast$ is free as a $\mathbf{Z}\left[v, v^{-1}\right]$-module.
So now using this construction, we can begin to describe the connection that Ringel noticed.
A quiver is a directed graph that generates a free category. More precisely, a quiver is a set of vertices $Q_0$, a set of arrows $Q_1$, and two functions $t$ and $h$, each from $Q_1$ to $Q_0$, that pick out the tail and head of an arrow respectively. The vertices of $Q_0$ correspond to the objects of the category generated by the quiver. The arrows of $Q_1$, along with some “identity arrows” $e_i$ that we assign to each vertex $i$ (so $t(e_i)=h(e_i)=i$), freely generate all the morphisms of the category. Hopefully without confusion, I’ll let $Q$ denote both the quiver and the free category it generates.
Consider a quiver $Q$ whose underlying (undirected) graph is one of the ADE Dynkin diagrams. Set $Q_0=I$ and let $\Delta$ be that underlying graph of $Q$. The Cartan matrix $A = (a_{ij})_{i,j \in I}$ corresponding to $\Delta$ has entries $a_{ii} = 2$, $a_{ij} = -1$ if there’s an edge between $i$ and $j$ in $\Delta$, and $a_{ij}=0$ otherwise. Then this Cartan matrix corresponds to a Lie algebra $\mathfrak{g} = \langle e_i, f_i \mid i \in I \rangle$ subject to the Chevalley-Serre relations:
\begin{gather*} \newcommand{\bracket}[2]{\left[#1\,#2\right]} \bracket{e_i}{f_j} = 0 \;\text{ for } i\neq j \\ \bracket{[e_i\,f_i]}{e_j} = a_{ij}e_j \qquad \bracket{[e_i\,f_i]}{f_j} = -a_{ij}f_j \\ \left(\mathrm{ad}_{e_i}\right)^{1-a_{ij}}(e_j) = 0 \qquad \left(\mathrm{ad}_{f_i}\right)^{1-a_{ij}}(f_j) = 0 \end{gather*}Then $\mathfrak{g}$, as a vector space, will decompose as $\mathfrak{g} = \mathfrak{n}_{-} \oplus \mathfrak{h} \oplus \mathfrak{n}_{+}$, where $\mathfrak{n}_{-}$ is the subalgebra generated by the $f_i$, $\mathfrak{n}_{+}$ is the subalgebra generated by the $e_i$, and $\mathfrak{h}$ is the Cartan subalgebra generated by $\bracket{e_i}{f_i}$. The subalgebra $\mathfrak{n}_{+}$ by itself then has a much simpler presentation, subject only to the relation $\left(\mathrm{ad}_{e_i}\right)^{1-a_{ij}}(e_j) = 0$. It’s universal enveloping algebra is then the associative algebra $\mathbf{U}(\mathfrak{n}_{+})$ generated as an algebra $\left\langle E_i \mid i \in I \right\rangle$ subject to that single relation written in terms of a literal commutator:
\begin{align*} E_iE_j-E_jE_i= 0 \quad&\text{for } a_{ij}=0 \\ E_i^2E_j-E_iE_jE_i+E_jE_i^2 = 0 \quad&\text{for } a_{ij}=-1 \,. \end{align*}We want to consider the $q$-deformation $\mathbf{U}_q(\mathfrak{n}_{+})$ of $\mathbf{U}(\mathfrak{n}_{+})$, the quantized enveloping algebra of $\mathfrak{n}_{+}$, constructed as follows: Let $q = v^2$ be indeterminates. Define the $\mathbf{Q}(v)$-algebra $\mathbf{U}'_q(\mathfrak{n}_{+})$ as being generated by $\langle E_i \mid i \in I\rangle$ subject to the relations
\begin{align*}\label{eq:relations}\tag{$\star$} E_iE_j-E_jE_i= 0 \quad&\text{for } a_{ij}=0 \\ E_i^2E_j-\left(v + v^{-1}\right)E_iE_jE_i+E_jE_i^2 = 0 \quad&\text{for } a_{ij}=-1 \,. \end{align*}Theses relations come from the quantum Serre relation defined on the whole quantized enveloping algebra $\mathbf{U}_q(\mathfrak{g})$ that only involves the generators $E_i$. Then $\mathbf{U}_q(\mathfrak{n}_{+})$ is the $\mathbf{Q}(v)$-subalgebra of $\mathbf{U}'_q(\mathfrak{n}_{+})$ spanned by $E_i^{(m)} := \frac{1}{[m]!}E_i^m$, still satisfying the relations (\ref{eq:relations}), where $[m]!$ is the $q$-factorial defined as
\begin{equation*} [m]! \;:=\; \prod_{k=0}^m \frac{q^k-q^{-k}}{q-q^{-1}} \,. \end{equation*}Now we go back and start with the same quiver $Q$ whose underlying graph is an ADE Dynkin diagram, but instead of taking the Lie theoretic route suggested by the fact that $Q$ corresponds to a Dynkin diagram, we’ll study the representations of $Q$ as a category. For a finite field $\boldsymbol{k}$, a representation of a quiver $Q$ is a functor from $Q$ to $\text{Vect}_\boldsymbol{k}$, the category of finite dimensional vector spaces over $\boldsymbol{k}$. Concretely, this is an assignment of vector spaces $X_i$ to each vertex $i \in Q_0$ and an assignment of linear maps $X_a \colon X_{t(a)} \to X_{h(a)}$ to each arrow $a \in Q_1$. A morphism of representations $\varphi \colon X \to Y$ is a collection of linear maps $\{\varphi_i \colon X_i \to Y_i\}_{i \in Q_0}$ such that for any arrow $a$ the following square commutes:
\begin{equation*} \require{AMScd} \begin{CD} X_{t(a)} @>{\varphi_{t(a)}}>> Y_{t(a)}\\ @V{X_a}VV @VV{Y_a}V\\ X_{h(a)} @>{\varphi_{h(a)}}>> Y_{h(a)} \end{CD} \end{equation*}The collection of all such representations forms an abelian $\boldsymbol{k}$-linear category $\text{Rep}_\boldsymbol{k} Q$. You could more concisely describe $\text{Rep}_\boldsymbol{k} Q$ as the functor category $\text{Vect}_\boldsymbol{k}^Q$, where objects are functors $Q \to \text{Vect}_\boldsymbol{k}$ and the morphisms are natural transformations. See Hubery’s Hall algebra notes for more details on quivers and their representations.
Furthermore, in this specific case, $\text{Rep}_\boldsymbol{k} Q$ is finitary since $\boldsymbol{k}$ is finite and is hereditary since $Q$ has no directed cycles. This means that we can consider its twisted Hall algebra $\mathbf{H}_{\text{Rep}_\boldsymbol{k} Q}^\ast$. Let $S_i$ denote the simple representation of $Q$ concentrated at node $i$, where $(S_i)_i = \boldsymbol{k}$ and $(S_i)_j = 0$ for $i \neq j$. For ease of notation, let $S_i$ also denote isomorphism class $[S_i] \in \mathbf{H}_{\text{Rep}_\boldsymbol{k} Q}^\ast$ containing the simple representation $S_i$.
The elements $S_i$ of $\mathbf{H}_{\text{Rep}_\boldsymbol{k} Q}^\ast$ corresponding to the isomorphism classes of simple representations of $Q$ satisfy the relations \begin{align*} S_iS_j-S_jS_i=0 \quad&\text{for } (i \to j) \notin Q_1 \\ S_i^2S_j-\left(v+v^{-1}\right)S_iS_jS_i+S_jS_i^2=0 \quad&\text{for } (i \to j) \in Q_1 \end{align*}
The first of these relations holds
since $S_iS_j=S_jS_i=S_i\oplus S_j$ if $(i \to j) \notin Q_1$.
For the second relation where $(i \to j) \in Q_1$,
we first calculate the products $S_iS_j$ and $S_jS_i$,
and the dimensions of $\mathrm{Hom}$ and $\mathrm{Ext}$
for these pairs of these simple modules:
\begin{gather*}
\mathrm{Hom}(S_i,S_j) = 0
\qquad
\mathrm{Hom}(S_j,S_i) = 0
\\
\mathrm{Ext}^1(S_i,S_j) = \boldsymbol{k}
\qquad
\mathrm{Ext}^1(S_j,S_i) = 0
\end{gather*}
There is a single isomorphism class of indecomposable representations that fits in an exact sequence $S_j \hookrightarrow X ↠ S_i$, corresponding to $\mathrm{Ext}^1(S_i, S_j) = \boldsymbol{k}$. Let’s just denote this isomorphism class $X$. \begin{gather*} S_iS_j = v^{-1}\left(S_i \oplus S_j + X\right) \qquad S_jS_i = S_i \oplus S_j \end{gather*}
Note that this implies $S_iS_j = vS_jS_i + v^{-1}X$. Using this fact, the second relation becomes \begin{align*} &S_i^2S_j-\left(v+v^{-1}\right)S_iS_jS_i+S_jS_i^2 \\ =\quad &S_i\left(vS_jS_i + v^{-1}X\right)-vS_iS_jS_i-v^{-1}\left(vS_jS_i + v^{-1}X\right)S_i+S_jS_i^2 \\ =\quad &v^{-1}S_iX - v^{-2}XS_i \,. \end{align*}
Now we’ll need to calculate $S_iX$ and $XS_i$. \begin{gather*} \mathrm{Hom}(S_i,X) = 0 \qquad \mathrm{Hom}(X,S_i) = \boldsymbol{k} \\ \mathrm{Ext}^1(S_i,X) = 0 \qquad \mathrm{Ext}^1(X,S_i) = 0 \\ S_iX = q\left(X \oplus S_i\right) \qquad XS_i = vq\left(X \oplus S_i\right) \end{gather*} This then gives us \begin{equation*} v^{-1}S_iX - v^{-2}XS_i \;\;=\;\; v^{-1}q\left(X \oplus S_i\right) - v^{-2}vq\left(X \oplus S_i\right) \;\;=\;\; 0 \,, \end{equation*} which is precisely what we want.
These are the same relations in (\ref{eq:relations}) that $\mathbf{U}_q(\mathfrak{n}_{+})$ satisfy, which suggests to the following theorem.
There is a $\mathbf{Z}\left[v,v^{-1}\right]$-algebra isomorphism $\mathbf{U}_q(\mathfrak{n}_{+}) \to \mathbf{H}_{\text{Rep}_\boldsymbol{k} Q}^\ast$, where $E_i \mapsto [S_i].$
In other words, for any ADE Dynkin diagram, and for any choice of orientation of the edges in the diagram to get a quiver $Q$, the category $\text{Rep}_\boldsymbol{k} Q$ is a categorification of $\mathbf{U}_q(\mathfrak{n}_{+})$, the “upper half” of the quantized enveloping algebra of the Lie algebra corresponding to that diagram. Among the benefits implicit to categorification already discussed, in The Hall Algebra Approach to Quantum Groups Ringel points out other useful consequences of this isomorphism. The algebra $\mathbf{U}_q(\mathfrak{n}_{+})$, as originally defined by Jimbo and Drinfeld in the 80s (see Drinfeld’s Quantum Groups paper) is usually presented in terms of generators and relations, whereas $\mathbf{H}_{\text{Rep}_\boldsymbol{k} Q}^\ast$ is constructed as a free $\mathbf{Z}\left[v, v^{-1}\right]$-module with a basis that only depends on the direction of the arrows in the original quiver, and structure constants that come cleanly from the structure of the category which, via the isomorphism, makes doing computations in $\mathbf{U}_q(\mathfrak{n}_{+})$ easier. On the other hand the algebra $\mathbf{U}_q(\mathfrak{n}_{+})$ gives us a new perspective on the representation theory of quivers and the study of their path algebras via theorems and tools from the study of Lie algebras and quantum groups. In particular these quantized enveloping algebras are PBW algebras, defined after the Poincaré-Birkhoff-Witt Theorem for semi-simple Lie algebras, as algebras generated by some ordered set $X_A$ that are freely generated as a vector space over ordered monomials in $X_A$ (see Lusztig’s Introduction to Quantum Groups book). This suggests a theorem, known for awhile but recently explored in greater generality in Berenstein’s and Greenstein’s Primitively Generated Hall Algebras paper about the structure of Hall algebras that come from sufficiently nice categories.
For a finitary exact Krull-Schmidt category $\mathcal{C}$, let $\mathrm{Ind}\mathcal{C}$ denote the set of isomorphism classes of indecomposable objects of $\mathcal{C}$. The Hall algbra $\mathbf{H}_\mathcal{C}$ is a PBW algebra on $\mathrm{Ind}\mathcal{C}$ as a $\mathbf{Q}$ vector space.
And this isomorphism $\mathbf{U}_q(\mathfrak{n}_{+}) \mathrel{\cong} \mathbf{H}_{\text{Rep}_\boldsymbol{k} Q}^\ast$ holds more generally too. Looking at representation-directed algebras, a generalization of path algebras of finite acyclic quivers, Ringel extended the above result to get an algebra isomorphic to the entire universal enveloping algebra of a lie algebra. Going a bit further in that same direction, Schofield extended this result to arbitrary symmetric Kac-Moody Lie algebras by looking at varieties of quiver representations over $\mathbf{C}$. The introduction in Hubery’s Ringel-Hall Algebras of Cyclic Quivers contains a brief summary of other results that extend this theorem of Ringel. The problem that I’ve been working on has been to analogously extend this result in the case of some quantum groups constructed in Berenstein’s and Greenstein’s Quantum Folding paper
Consider again a Dynkin diagram corresponding to a semi-simple Lie algebra $\mathfrak{g}$. There is the classic idea of “folding” the diagram of $\mathfrak{g}$ along an admissible diagram automorphism $\sigma$ to obtain a new semi-simple Lie algebra $\mathfrak{g}^{\sigma}$, the Langland’s dual to the fixed Lie subalgebra $\mathfrak{g}^\sigma = \{x \in \mathfrak{g} \mid \sigma(x) = x\}$. For example, for a Dynkin diagram of type $D_{n+1}$ corresponding to $\mathfrak{g} = \mathfrak{so}_{2n+2}$, there is a diagram automorphism $\sigma$ that swaps the two nodes of the fork in $D_{n+1}$ and fixes all other nodes. So we can then “fold” these nodes together, creating a new diagram with nodes corresponding to the orbits of $\sigma$:

The new diagram is of type $C_n$ and corresponds to the Langland’s dual of the fixed-point Lie subalgebra $\mathfrak{g}^\sigma = \mathfrak{so}_{2n+1} \hookrightarrow \mathfrak{so}_{2n+2}$. In Quantum Folding this technique is extended to the quantized enveloping algebras of corresponding pairs of folded Lie algebras.
For $\mathfrak{g}$ of type $D_{n+1}$, there exists a quantum folding \begin{equation*} \iota \colon \mathbf{U}_q^{+}\left(\mathfrak{g}^{\sigma\vee}\right) \hookrightarrow % \mathbf{U}_q^{+}(\mathfrak{g})^{\sigma} \subset % \mathbf{U}_q^{+}(\mathfrak{g}) \end{equation*} and a corresponding quantum group $U(\iota)$ which is a minimal PBW cover of the image of $\iota$.
This map $\iota$ is not an algebra morphism, but is only $\mathbf{C}(q)$-linear, so the image of $\iota$ is not the “folding” we were hoping for. This the purpose of $U(\iota)$. The map $\iota$ factors through $U(\iota)$ as follows, giving us the map $\tilde{\iota}$ that is the folding of algebras we’re really after.
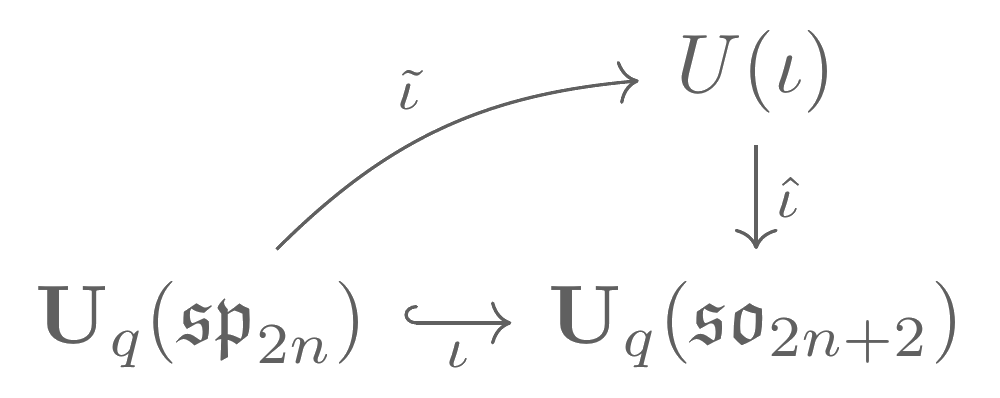
In the Quantum Folding paper, $U(\iota)$ is described only in terms of generators and relations. The aim of my research right now is to be able to describe $U(\iota)$ in terms of the Hall algebra of $\text{Rep}_\boldsymbol{k} D_{n+1}$, or of $\text{Rep}_\boldsymbol{k} C_n$, or at least somehow coming from a quiver related to the $D_{n+1}$ or $C_n$ Dynkin diagrams. That is, I’m trying to categorify this quantum folding construction.