 |
 |
Lecture 10 - The Logic of Partitions
I've been explaining how we can create a version of logic starting from any poset, which we think of as a poset of "propositions". There are various ways to get our hands on such a poset. One way is to start with a set \( X \) and build a poset \( P X \) whose elements are subsets of \( X \). This leads to the most traditional form of logic, called classical logic. But another way is to start with a set \( X \) and build a poset \( \mathcal{E}(X) \) whose elements are "partitions" of \( X \). This leads to another form of logic, called the logic of partitions.
What's a partition? It's a way of chopping the set \( X \) into "parts". We want each part to be a nonempty subset of \( X \), we want these parts to be disjoint, and we want their union to be all of \( X \). For example, here are all 52 partitions of a set with 5 elements:
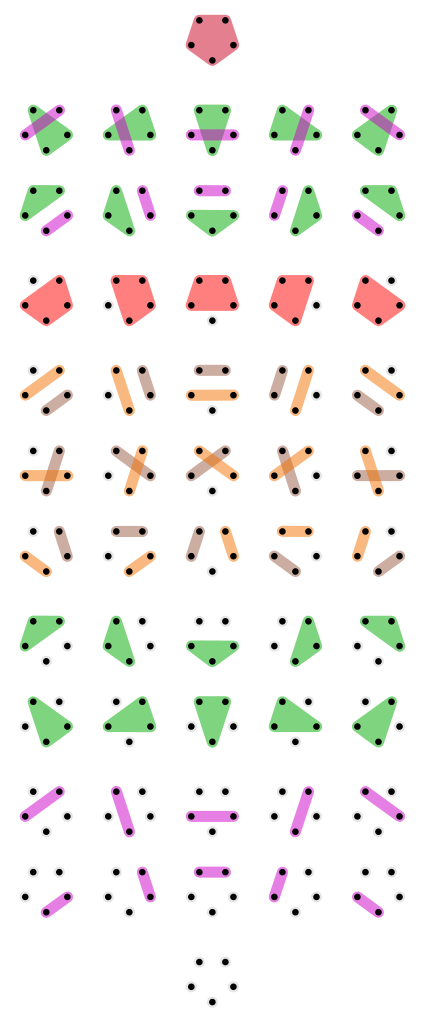
At the top we see the "coarsest" partition, where all 5 elements are in the same part. At the bottom we see the "finest" partition, where each element is in its own separate part.
How can we think of these partitions as "propositions"? Here's how: each partition gives a proposition saying that two elements in the same part are "equivalent", or the same in some way. The coarser the partition, the more elements are equivalent.
For example, imagine you're a detective trying to solve a case on a small island with 5 people on it. At first you don't know any of them are related, so they're all in separate families, as far as you know:

But then you start digging into their history. Each time you learn that two people are related, you change your partition by putting them into the same part:

You keep doing this as secret family relationships are revealed:

In this example, as you learn more you move to coarser partitions, because your goal is to find relationships between people, and lump them in as big bunches as possible. But often people think about partition logic a bit differently, where as you learn more you move to finer partitions.
Suppose you are an amateur wine taster learning to distinguish different kinds of wine by their taste. At first all wines taste alike, so they're all lumped together:

When you learn to distinguish red and white wines, you move to a finer partition:

This sort of example will fit our story a bit better. We'll generally say that you know more if your partition is finer.
Now it's time to define partitions more carefully! A partition of \(X\) is a bunch of subsets of \(X\). So, it's a subset of \(P(X)\). Please think about that until it makes sense, or ask questions. There are a lot of sets and subsets running around: it can be confusing. But here we go:
Definition. A partition of a set \(X\) is a set \(P \subseteq P(X)\) such that:
-
Each set \(S \in P \) is nonempty.
-
Distinct sets \(S, T \in P\) are disjoint: that is, if \(S \ne T\) then \(S \cap T = \emptyset \).
-
The union of all the sets \(S \in P\) is \(X\): that is,
[ X = \bigcup_{S \in P} S .]
We call the sets \(S \in P\) the parts of the partition.
I said that each partition \(P\) gives an equivalence relation, where two elements of \(X\) are "equivalent" if and only if they're in the same part. Let's make that precise too:
Definition. An equivalence relation on a set \(X\) is a relation \(\sim\) on \(X\) that is:
-
Reflexive: for all \(x \in X\), \(x \sim x\).
-
Transitive: for all \(x,y,z \in Z\), \(x \sim y \) and \(y \sim z\) imply \(x \sim z\).
-
Symmetric: for all \(x,y \in X\), \(x \sim y\) implies \(y \sim x.\)
Puzzle 28. Show that if \(P\) is a partition of a set \(X\), and we define a relation \(\sim_P\) on \(X\) as follows:
[ x \sim_P y \textrm{ if and only if } x, y \in S \textrm{ for some } S \in P, ]
then \(\sim_P \) is an equivalence relation.
Puzzle 29. Show that if \(\sim\) is an equivalence relation on a set \(X\), we can define a partition \(P_\sim\) on \(X\) whose parts are precisely the sets of the form
[ S_x = \{y \in X : \; y \sim x \} ]
with \(x \in X\). We call \(S_x\) the equivalence class of \(x\).
Puzzle 31. Show that the previous two puzzles give a one-to-one correspondence between partitions of \(X\) and equivalence relations on \(X\).
Puzzle 32. Proposition 1.11 of Seven Sketches asserts that there is a one-to-one correspondence between partitions of \(X\) and equivalence relations on \(X\). However, in the current version of the book this proposition is false! Nonetheless, the statement in Puzzle 31 is correct. How is this possible? (Hint: you have to read their definitions quite carefully. This is good practice in reading mathematics.)
Puzzle 33. Is an equivalence relation always a preorder?
To read other lectures go here.
 |
 |