Lecture 38 - Functors

Last time we saw a graph that could be used for designing databases:

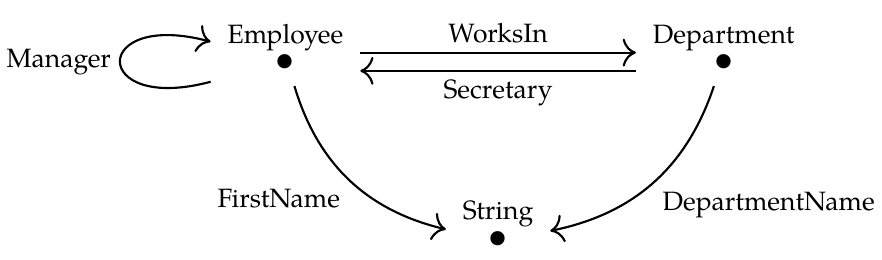
This graph is not a database; it's just a kind of template for a database. Fong and Spivak call it a database schema. To create an actual database using this schema, you'd have to specify:

• a set of employees
• a set of departments
• a set of strings (that is, strings of symbols)
• a function mapping each employee to the department they work in
• a function mapping each employee to their manager
• a function mapping each department to its secretary
• a function mapping each employee to their first name
• a function mapping each department to its name.

You could do this using a table or spreadsheet, or some other way. See the start of Chapter 3 for more on this!

What does this have to do with category theory? A lot!

We've seen that this "database schema" is really a graph \(G\). And we saw that from a graph we can get a category \(\mathbf{Free}(G)\) called the "free category on \(G\)". This has nodes of the graph as objects and paths as morphisms.

So, our database schema gives a category \(\mathbf{Free}(G)\). The objects in this category are things like \(\textrm{Employee}\) and \(\textrm{Department}\). The morphisms are things like \(\textrm{WorksIn} : \textrm{Employee} \to \textrm{Department}\).

To get an actual database, we need to provide a set for each object of \(\mathbf{Free}(G)\), and a function for each morphism of \(\mathbf{Free}(G)\).

When we do this, we're providing some sort of map from the category \(\mathbf{Free}(G)\) to the category \(\textbf{Set}\). A map between categories is called a "functor": it sends objects to objects, and morphisms to morphisms... and it should also obey a few obvious rules, which I'll explain in a second.

But first, enjoy the beauty of this idea! A database schema is really a category, while an actual database is a functor from that category to \(\textbf{Set}\). The database schema has "abstract" objects and morphisms like \(\textrm{Employee}\) and \(\textrm{WorksIn} : \textrm{Employee} \to \textrm{Department}\), while the functor makes these "concrete", turning them into actual sets and functions!

So what's a functor, exactly?

Definition. Given categories \(\mathcal{C}\) and \(\mathcal{D}\), a functor from \(\mathcal{C}\) to \(\mathcal{D}\), written \(F: \mathcal{C} \to \mathcal{D} \), consists of:

1. A function sending objects of \(\mathcal{C}\) to objects of \(\mathcal{D}\). This is usually called \(F\) as well, so we have \(F: \mathrm{Ob}(\mathcal{C}) \to \mathrm{Ob}(\mathcal{D}) \).

2. For each pair of objects \(x,y \in \mathrm{Ob}(\mathcal{C})\), a function sending each morphism \(f: x \to y\) to a morphism \(F(f) : F(x) \to F(y) \). As you can see, we're calling this function \(F\) too! So, it's a function

[ F: \mathcal{C}(x,y) \to \mathcal{D}(F(x),F(y)) .]

Remember, \(\mathcal{C}(x,y)\) is the set of morphisms from \(x\) to \(y\) in \(\mathcal{C}\).

We demand that:

a) \(F\) preserves composition: \(F(g \circ f) = F(g) \circ F(f) \) whenever \(f\) and \(g\) are morphisms that can be composed in \(\mathcal{C}\).

b) \(F\) preserves identities: \(F(1_x) = 1_{F(x)}\) whenever \(x\) is an object of \(\mathcal{C}\).

That's it!

It may freak you out that we're using \(F\) to mean the functor, the function that describes what this functor does to objects, and all the functions that describe what \(F\) does to morphisms. However, this turns out not to be a problem. It would be much worse to have separate notations for all these things. You should think of them all as a single package: \(F\).

You may wonder about conditions a) and b). They seem to have shown up by magic. How do they arise in our study of databases?

Here's an example. Take \(\mathcal{C} = \mathbf{Free}(G)\) and look at the morphisms \(\textrm{WorksIn} : \textrm{Employee} \to \textrm{Department}\) and \(\textrm{DepartmentName} : \textrm{Department} \to \textrm{String}\). Then choose a functor \(F : \mathcal{C} \to \mathbf{Set}\). We must have

[ F(\textrm{DepartmentName} \circ \textrm{WorksIn}) = F(\textrm{DepartmentName}) \circ F(\textrm{WorksIn}) . ]

Puzzle 109. What does this mean, in practical terms?

There's a lot more to say, but not now!

To read other lectures go here.