Lecture 39 - Databases

Last time we saw how to treat a graph \(G\) as a 'database schema' and then consider databases built using this schema. The idea is to form the category

[ \mathcal{C} = \mathbf{Free}(G) ]

whose morphisms are paths in \(G\). Then, a database built using this schema is a functor

[ F: \mathcal{C} \to \mathbf{Set} .]

Elegant and simple! Remember, objects of \(\mathcal{C}\) are just nodes of the graph \(G\), like the node \(\textrm{Employee}\) in this graph:

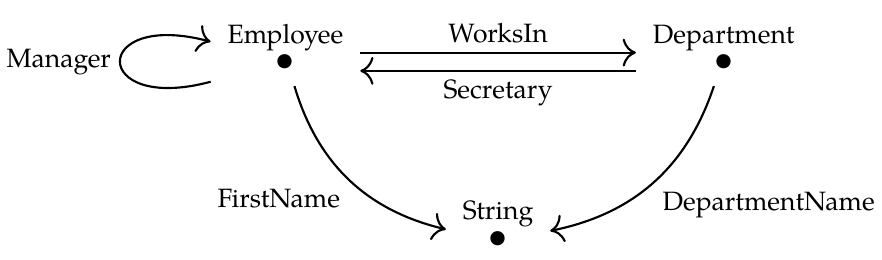
Then, our functor \(F\) sends each object to an actual set. For example, \(F(\textrm{Employee})\) will be the actual set of employees in our database!

The functor also sends each morphism in \(\mathcal{C}\) to an actual function. For example,

[ F(\textrm{WorksIn}): F(\textrm{Employee}) \to F(\textrm{Department}) ]

will be the function mapping each employee in our database to their department.

Since each edge of our graph gives a morphism in \(\mathcal{C}\), our database needs to specify a function for each edge. And these functions can be whatever you want! It takes a bit of thought to see this is true.

More generally, each path in our graph gives a morphism in \(\mathcal{C}\). So actually our database needs to specify a function for each path. But in fact those are all determined, once we specify a function for each edge.

Let's see how it works in our example. There's a morphism

[ \textrm{DepartmentName} \circ \textrm{WorksIn} : \textrm{Employee} \to \textrm{String} ]

in our category \(\mathcal{C}\), coming from a path of length 2 in our graph. So when we build a database, it must specify a function

[ F(\textrm{DepartmentName} \circ \textrm{WorksIn}) : F(\textrm{Employee}) \to F(\textrm{String}). ]

However, a functor must preserve composition: we always have \(F(f \circ g) = F(f) \circ F(g)\). So, we must have

[ F(\textrm{DepartmentName} \circ \textrm{WorksIn}) = F(\textrm{DepartmentName}) \circ F(\textrm{WorksIn}) .]

I hope this makes complete sense intuitively — see the answers to Puzzle 109 if it doesn't. It also means we don't have any choice about the function \(F(\textrm{DepartmentName} \circ \textrm{WorksIn})\) once we've picked the functions \(F(\textrm{DepartmentName})\) and \(F(\textrm{WorksIn})\). In fact, knowing what \(F\) does to edges completely determines what it does to all paths of length \(1, 2, 3, \) and so on!

In summary: when our database schema is \(\mathcal{C} = \mathbf{Free}(G)\), to specify a database we simply:

Choose any set \(F(x)\) for each node \(x\) of our graph.
Choose any function \(F(e) : F(x) \to F(y)\) for each edge \(e\) in our graph, where \(x\) is the source and \(y\) is the target of that edge.

I haven't actually proved this; I'm just trying to make it plausible. Anyway, it's true, and this 'complete freedom' in choosing sets for nodes and functions for edges is why \(\mathbf{Free}(G)\) is called the 'free category' on the graph \(G\).

Puzzle 110. I said that knowing \(F\) does to edges completely determines what it does to paths of length \(1, 2, 3, \) and so on, due to the rule \(F(f \circ g) = F(f) \circ F(g)\). But what about paths of length 0?

All this is very pretty. But what if we want to impose some extra constraints on our database? In the answers to Puzzle 106 we saw two constraints we might want to impose. To keep things simple let's just look at one:

The secretary of any department works in that department.

Constraints of this general sort can be handled using 'finitely presented' categories. To get one of these, we suppose our graph \(G\) is finite — if it's not, our database will be awfully big. Then, we replace the free category \(\mathcal{C} = \mathbf{Free}(G)\) by a new category, say \(\mathcal{D}\), in which we impose finitely many extra equations between morphisms.

In the example above, we'd impose this equation:

\( \mathrm{WorksIn} \circ \mathrm{Secretary} = 1_{\mathrm{Department}}.\)

This equation may imply other equations, but that's okay.

Allowing equations between morphisms gives a more general, more powerful concept of database schema. Now a database schema is a finitely presented category \(\mathcal{D}\), and a database built using this schema is a functor \(F : \mathcal{D} \to \mathbf{Set}\).

In our example, where we've imposed the equation

[ \mathrm{WorksIn} \circ \mathrm{Secretary} = 1_{\mathrm{Department}} , ]

the fact that \(F\) is a functor will imply

[ F( \mathrm{WorksIn}) \circ F(\mathrm{Secretary}) = 1_{F(\mathrm{Department})}]

So, only a database where this equation holds is allowed, if we're using this particular category \(\mathcal{D}\) as our schema! When you enter data, you have to check this equation.

So, our procedure for creating databases gets an extra step:

Choose any set \(F(x)\) for each node \(x\) of our graph.
Choose a function \(F(e) : F(x) \to F(y)\) for each edge \(e\) in our graph, where \(x\) is the source and \(y\) is the target of that edge.
Check that each equation \(F(f) = F(g)\) holds, whenever \(f = g\) is an equation between paths that we've imposed when defining our finitely presented category \(\mathcal{D}\).

The last step is bit of a nuisance, though it's not hard to do. As usual, adding more power to our setup makes it more complicated to use. But it may be worthwhile.

Puzzle 111. Suppose every person has one best friend. We get a database schema as possible. Start with a graph \(G\) having one node \(\textrm{Person}\) and one edge \(\textrm{BestFriend}\) from that node to itself. This gives a free category \(\mathcal{C} = \mathbf{Free}(G)\). Use this as our database schema. How many databases built on this schema are possible if

[ F(\textrm{Person}) = \{ \textrm{Anna}, \textrm{Jordan}, \textrm{Lisa}, \textrm{Ryan} \} ?]

Puzzle 112. Now suppose every person is their best friend's best friend:

[ \textrm{BestFriend} \circ \textrm{BestFriend} = 1_{\textrm{Person}} .]

Create the finitely presented category \(\mathcal{D}\) by taking the free category \(\mathcal{C}\) and imposing this equation. How many databases built on this schema \(\mathcal{D}\) are possible if again we have

[ F(\textrm{Person}) = \{ \textrm{Anna}, \textrm{Jordan}, \textrm{Lisa}, \textrm{Ryan} \} ?]

Puzzle 113. What if every person is their best friend's best friend's best friend?

To read other lectures go here.