Lecture 45 - Composing Natural Transformations

I told you about categories. I told you about functors. Now I'm going to tell you about functor categories!

I remember how this kind of thing used to make me panic. I had learned a couple of concepts in category theory, and I had them neatly separate in my mind - but then someone combined them in a way that was new to me, and my brain short-circuited. Eventually I realized these combinations are exactly what makes category theory so powerful, and I grew to enjoy them.

But in this particular case there's really no need to panic. You may know the idea of a set of functions, like the set of all functions from a set \(X\) to a set \(Y\). This is called \(Y^X\). That may look backwards, but there's a good reason: there are \(3^7\) functions from a \(7\)-element to a \(3\)-element set.

Just as you can form a set of functions, you can form a category of functors. There's a category of all functors from a category \(\mathcal{C}\) to a category \(\mathcal{D}\). It's called \(\mathcal{D}^\mathcal{C}\).

How does it work? The objects of \(\mathcal{D}^\mathcal{C}\) are just functors from \(\mathcal{C}\) to a category \(\mathcal{D}\). That's the easy part. But what are the morphisms?

The morphisms are natural transformations!

You should have seen that coming. When we have two functors \(F,G : \mathcal{C} \to \mathcal{D}\), we can talk about natural transformations from \(F\) to \(G\). We write these using double arrows, like \(\alpha: F \Rightarrow G\), just so they look different from functors. And now I'm just saying we should take these double arrows seriously: a natural transformation \(\alpha: F \Rightarrow G\) is a kind of morphism from \(F\) to \(G\).

But the big question is: how do we compose these guys?

Here's how:

Definition. Let \(\mathcal{C}\) and \(\mathcal{D}\) be categories, let \(F,G,H : \mathcal{C} \to \mathcal{D}\) be functors, and let \(\alpha : F \Rightarrow G\) and \(\beta : G \Rightarrow H\) be natural transformations. Then there is a natural transformation \(\beta \circ \alpha : F \Rightarrow H\), called the composite of \(\alpha\) and \(\beta\), defined as follows:

[ (\beta \circ \alpha)_x = \beta_x \circ \alpha_x ]

for any object \(x \in \mathcal{C} \).

This is a reasonable definition. After all,

[ \alpha_x : F(x) \to G(x) ]

and

[ \beta_x : G(x) \to H(x) ]

so they are just dying to be composed to give

[ \beta_x \circ \alpha_x : F(x) \to H(x) .]

But we still need to check that this gives a natural transformation! Remember, for a transformation to be natural we need a bunch of 'naturality squares' to commute.

Let's check this out. Since \(\alpha\) is natural we know that for any morphism \(f: x \to y\) in \(\mathcal{C}\) this square commutes:

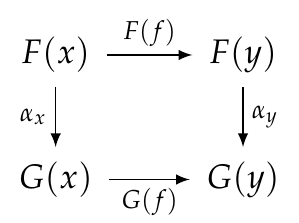
Remember, that just means that going down and then across is equal to going across and then down:

[ G(f) \circ \alpha_x = \alpha_y \circ F(f) .]

Similarly, since \(\beta\) is natural we know that this square commutes:

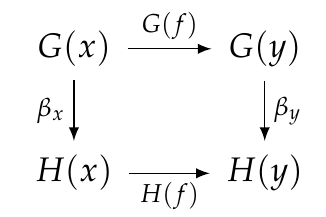
or in other words, this equation holds:

[ H(f) \circ \beta_x = \beta_y \circ G(f) .]

We need to show that \(\beta \circ \alpha\) is natural, meaning that this square commutes:

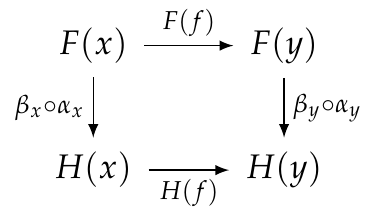
or in other words

[ H(f) \circ \beta_x \circ \alpha_x = \beta_y \alpha_y F(f) .]

We can prove this equation using the previous two, like this:

[ H(f) \circ \beta_x \circ \alpha_x = \beta_y \circ G(f) \circ \alpha_x = \beta_y \circ \alpha_y \circ F(f) . ]

Yay!

Please make sure you follow this simple calculation perfectly. Don't gloss over it, really think about it! Here's another way to think about it. We can take the naturality squares for \(\alpha\) and \(\beta\) and stick them together, like this:

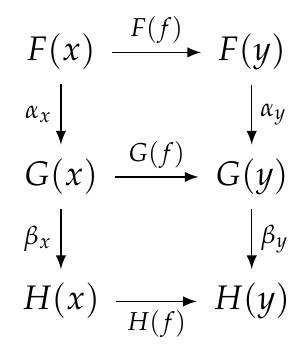
For each square, down and then across = across and then down. So, this is true for the whole big rectangle! That gives us the naturality square we need:

This kind of reasoning with diagrams turns out to be easier than messing with equations. When you get good at it, you just draw a bunch of squares and triangles and other shapes and stare at them and see that what you want is true! It's called 'diagram chasing'.

So, we can compose two natural transformations and get another natural transformations. We also have 'identity' natural transformations:

Definition. For any functor \(F : \mathcal{C} \to \mathcal{D}\) there is an identity natural transformation \(1_F : F \Rightarrow F\), with

[ (1_F)_x = 1_x ]

for all \(x \in \mathcal{C}\).

So, we're well on our way to getting a category where objects are functors from \(\mathcal{C}\) to \(\mathcal{D}\) and morphisms are natural transformations between such functors! But we've got to check some stuff:

Puzzle 140. Show that \(1_F : F \Rightarrow F\), defined this way, really is natural.

Puzzle 141. Prove the left and right unit laws: for any natural transformation \(\alpha: F \Rightarrow G\) we have

[ 1_G \circ \alpha = \alpha = \alpha \circ 1_F .]

Puzzle 142. Prove the associative law: for any natural transformations \(\alpha: F \Rightarrow G\), \(\beta: G \Rightarrow H\) and \(\gamma: H \Rightarrow I \) we have

[ (\gamma \circ \beta) \circ \alpha = \gamma \circ (\beta \circ \alpha). ]

That's all we need to check! So now we're ready to announce our result and celebrate!

Theorem. For any categories \(\mathcal{C}\) and \(\mathcal{D}\) there is a functor category \(\mathcal{D}^\mathcal{C}\) where:

objects are functors from \(\mathcal{C}\) to \(\mathcal{D}\),
morphisms are natural transformations between such functors,
composition and identities are defined as above.

Great!

What next? Well, you should think about how this relates to databases:

Puzzle 143. Make up an example of three databases built using the same schema, say \(F,G,H : \mathcal{C} \to \mathbf{Set}\). Make up some natural transformations \(\alpha : F \Rightarrow G\) and \(\beta : G \Rightarrow H\), and figure out what happens when you compose them.

But the fun with databases will really start when we understand adjoint functors and 'Kan extensions'. Everything I've done for the last few days is leading up to that material. It's some of the most important, fundamental category theory there is!

To read other lectures go here.