Lecture 44 - Categories, Functors and Natural Transformations

Last time I introduced natural transformations, and I think it's important to solve a bunch more puzzles to get a feel for what they're like. First I'll remind you of the basic definitions. I'll go through 'em quickly and informally:

Definition. A category \(\mathcal{C}\) consists of:

a collection of objects and
a set of morphisms \(f : x \to y\) from any object \(x\) to any object \(y\),

such that:

a) each pair of morphisms \(f : x \to y\) and \(g: y \to z\) has a composite \(g \circ f : x \to z \) and

b) each object \(x\) has a morphism \(1_x : x \to x\) called its identity,

for which

i) the associative law holds: \(h \circ (g \circ f) = (h \circ g) \circ f\), and

ii) the left and right unit laws hold: \(1_y \circ f = f = f \circ 1_x \) for any morphism \(f: x \to y\).

A category looks like this:

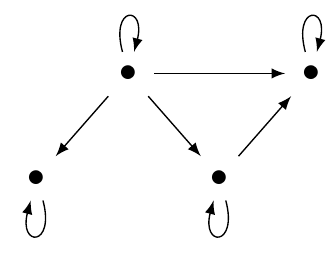
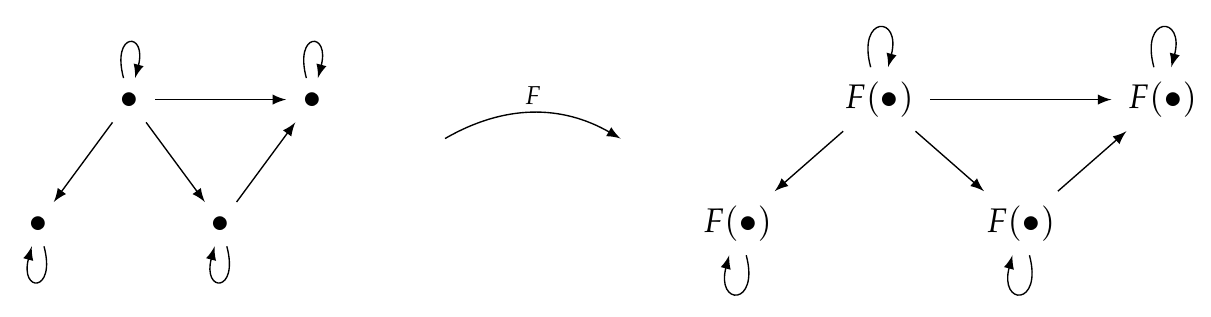
Definition. Given categories \(\mathcal{C}\) and \(\mathcal{D}\), a functor \(F: \mathcal{C} \to \mathcal{D} \) maps

each object \(x\) of \(\mathcal{C}\) to an object \(F(x)\) of \(\mathcal{D}\),
each morphism \(f: x \to y\) in \(\mathcal{C}\) to a morphism \(F(f) : F(x) \to F(y) \) in \(\mathcal{D}\) ,

in such a way that:

a) it preserves composition: \(F(g \circ f) = F(g) \circ F(f) \), and

b) it preserves identities: \(F(1_x) = 1_{F(x)}\).

A functor looks sort of like this, leaving out some detail:

Definition. Given categories \(\mathcal{C},\mathcal{D}\) and functors \(F, G: \mathcal{C} \to \mathcal{D}\), a natural transformation \(\alpha : F \to G\) is a choice of morphism

[ \alpha_x : F(x) \to G(x) ]

for each object \(x \in \mathcal{C}\), such that for each morphism \(f : x \to y\) in \(\mathcal{C}\) we have

[ G(f) \alpha_x = \alpha_y F(f) ,]

or in other words, this naturality square commutes:

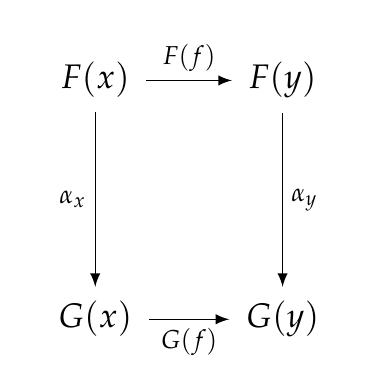
A natural transformation looks sort of like this:

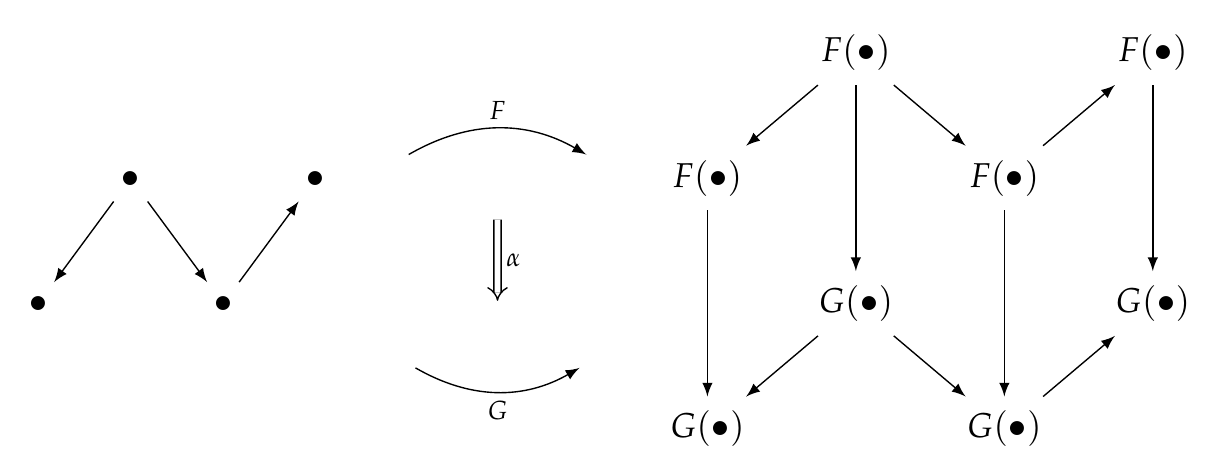
You should also review the free category on a graph if you don't remember that.

Okay, now for a bunch of puzzles! If you're good at this stuff, please let beginners do the easy ones.

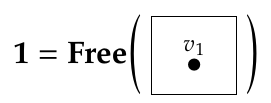
Puzzle 129. Let \(\mathbf{1}\) be the free category on the graph with one node and no edges:

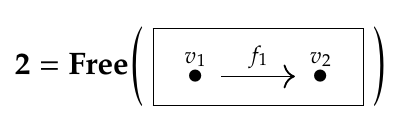
Let \(\mathbf{2}\) be the free category on the graph with two nodes and one edge from the first node to the second:

How many functors are there from \(\mathbf{1}\) to \(\mathbf{2}\), and how many natural transformations are there between all these functors? It may help to draw a graph with functors \(F : \mathbf{1} \to \mathbf{2} \) as nodes and natural transformations between these as edges.

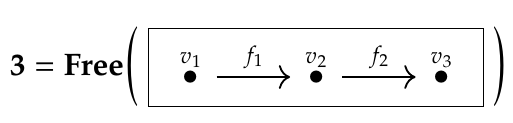
Puzzle 130. Let \(\mathbf{3}\) be the free category on this graph:

How many functors are there from \(\mathbf{1}\) to \(\mathbf{3}\), and how many natural transformations are there between all these functors? Again, it may help to draw a graph showing all these functors and natural transformations.

Puzzle 131. How many functors are there from \(\mathbf{2}\) to \(\mathbf{3}\), and how many natural transformations are there between all these functors? Again, it may help to draw a graph.

Puzzle 132. For any category \(\mathcal{C}\), what's another name for a functor \(F: \mathbf{1} \to \mathcal{C}\)? There's a simple answer using concepts you've already learned in this course.

Puzzle 133. For any category \(\mathcal{C}\), what's another name for a functor \(F: \mathbf{2} \to \mathcal{C}\)? Again, there's a simple answer using concepts you've already learned here.

Puzzle 134. For any category \(\mathcal{C}\), what's another name for a natural transformation \(\alpha : F \Rightarrow G\) between functors \(F,G: \mathbf{1} \to \mathcal{C}\)? Yet again there's a simple answer using concepts you've learned here.

Puzzle 135. For any category \(\mathcal{C}\), what are functors \(F : \mathcal{C} \to \mathbf{1} \) like?

Puzzle 136. For any natural number \(n\), we can define a category \(\mathbf{n}\) generalizing the categories \(\mathbf{1},\mathbf{2}\) and \(\mathbf{3}\) above: it's the free category on a graph with nodes \(v_1, \dots, v_n\) and edges \(f_i : v_i \to v_{i+1}\) where \(1 \le i < n\). How many functors are there from \(\mathbf{m}\) to \(\mathbf{n}\)?

Puzzle 137. How many natural transformations are there between all the functors from \(\mathbf{m}\) to \(\mathbf{n}\)?

I think Puzzle 137 is the hardest; here are two easy ones to help you recover:

Puzzle 138. For any category, what are functors \(F : \mathbf{0} \to \mathcal{C}\) like?

Puzzle 139. For any category, what are functors \(F : \mathcal{C} \to \mathbf{0} \) like?

To read other lectures go here.