Lecture 58 - Composing Feasibility Relations

In the puzzles last time we saw something nice: a feasibility relation between preorders is a generalization of something we learned about a long time ago: a monotone function between preorders.

But the really cool part is this: given preorders \(X\) and \(Y\), we can get a feasibility relation \(\Phi : X \nrightarrow Y\) either from a monotone function \(f : X \to Y\) or from a monotone function \(g: Y \to X\). So, feasibility relations put monotone functions going forwards from \(X\) to \(Y\) and those going backwards from \(Y\) to \(X\) into a common framework!

Even better, we saw that one of our favorite themes, namely adjoints, is deeply connected to this idea. Let me state this as a theorem:

Theorem. Let \(f : X \to Y \) and \(g: Y \to X\) be monotone functions between the preorders \(X\) and \(Y\). Define the feasibility relations \(\Phi : X \nrightarrow Y\) by

[ \Phi(x,y) \text{ if and only if } f(x) \le y ]

and

[ \Psi(x,y) \text{ if and only if } x \le g(y) .]

Then \(\Phi = \Psi\) if and only if \(f \) is the left adjoint of \(g\).

Proof. We have \(\Phi = \Psi\) iff

[ \Phi(x,y) \text{ if and only if } \Psi(x,y) ]

for all \(x \in X, y \in Y\), but by our definitions this is true iff

[ f(x) \le y \text{ if and only if } x \le g(y) ]

which is true iff \(f\) is the left adjoint of \(g\). \( \qquad \blacksquare \)

Ah, if only all proofs were so easy!

Now, to make feasibility relations into a truly satisfactory generalization of monotone functions, we should figure out how to compose them. Luckily this is easy, because we already know how to compose relations from Lecture 40. So, we should try to prove this:

Theorem. Suppose that \(\Phi : X \nrightarrow Y, \Psi : Y \nrightarrow Z\) are feasibility relations between preorders. Then there is a composite feasibility relation

[ \Psi \Phi : X \nrightarrow Z ]

defined as follows:

[ (\Psi \Phi)(x,z) = \text{true} ]

if and only if for some \(y \in Y\),

[ \Phi(x,y) = \text{true} \text{ and } \Psi(y,z) = \text{true}. ]

Puzzle 176. Prove this! Show that \(\Psi \Phi\) really is a feasibility relation.

I hope you see how reasonable this form of composition is. Think of it in terms of our pictures from last time:

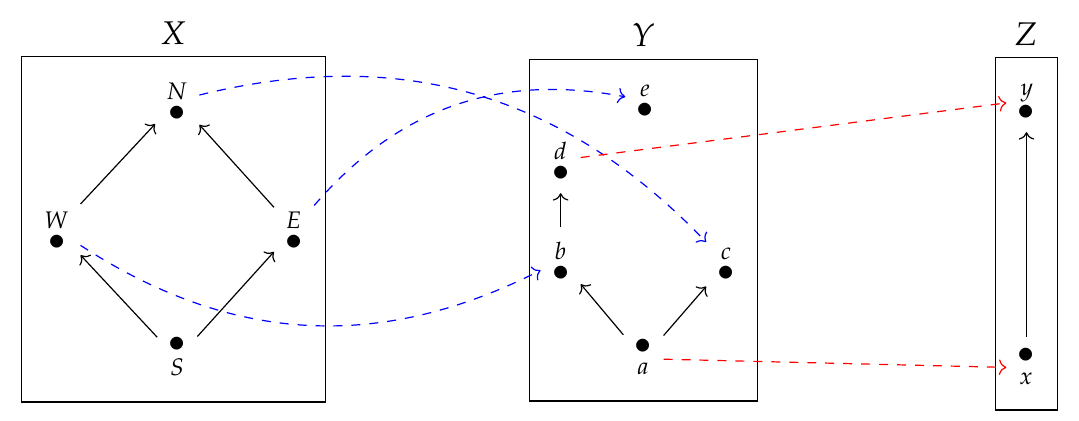
Here we have three preorders \(X,Y,Z\), which we can think of as cities with one-way roads. We can also take one-way airplane flights from \(X\) to \(Y\) and from \(Y\) to \(Z\): the flights in blue are a way of drawing a feasibility relation \(\Phi: X \nrightarrow Y\), and the flights in red are a way of drawing \(\Psi: Y \nrightarrow Z\).

Puzzle 177. Is \( (\Psi\Phi)(N,y) = \text{true}\)?

Puzzle 178. Is \( (\Psi\Phi)(W,y) = \text{true}\)?

Puzzle 179. Is \(( \Psi\Phi)(E,y) = \text{true}\)?

Puzzle 180. Prove that there is a category \(\textbf{Feas}\) whose objects are preorders and whose morphisms are feasibility relations, composed as above.

Puzzle 181. Suppose that \(\Phi : X \nrightarrow Y, \Psi : Y \nrightarrow Z\) are feasibility relations between preorders. Prove that

[ (\Psi\Phi)(x,z) = \bigvee_{y \in Y} \Phi(x,y) \wedge \Psi(y,z) ]

where \(\wedge\) is the meet in the poset \(\textbf{Bool}\), and \(\bigvee\) is the join. How is this formula related to matrix multiplication?

You may remember that a feasibility relation is a \(\mathcal{V}\)-enriched profunctor in the special case where \(\mathcal{V} = \textbf{Bool}\). This formula will be the key to defining composition for more general \(\mathcal{V}\)-enriched profunctors. But we need to talk about that more.

To read other lectures go here.