Lecture 59 - Cost-Enriched Profunctors

Lecture 59 - Cost-Enriched Profunctors

We've been looking at feasibility relations, as our first example of enriched profunctors. Now let's look at another example. This combines many ideas we've discussed - but don't worry, I'll review them, and if you forget some definitions just click on the links to earlier lectures!

Remember, \(\mathbf{Bool} = \lbrace \text{true}, \text{false} \rbrace \) is the preorder that we use to answer true-or-false questions like

while \(\mathbf{Cost} = [0,\infty] \) is the preorder that we use to answer quantitative questions like

or

In \(\textbf{Cost}\) we use \(\infty\) to mean it's impossible to get from here to there: it plays the same role that \(\text{false}\) does in \(\textbf{Bool}\). And remember, the ordering in \(\textbf{Cost}\) is the opposite of the usual order of numbers! This is good, because it means we have

[ \infty \le x \text{ for all } x \in \mathbf{Cost} ]

just as we have

[ \text{false} \le x \text{ for all } x \in \mathbf{Bool} .]

Now, \(\mathbf{Bool}\) and \(\mathbf{Cost}\) are monoidal preorders, which are just what we've been using to define enriched categories! This let us define

and

We can draw preorders using graphs, like these:

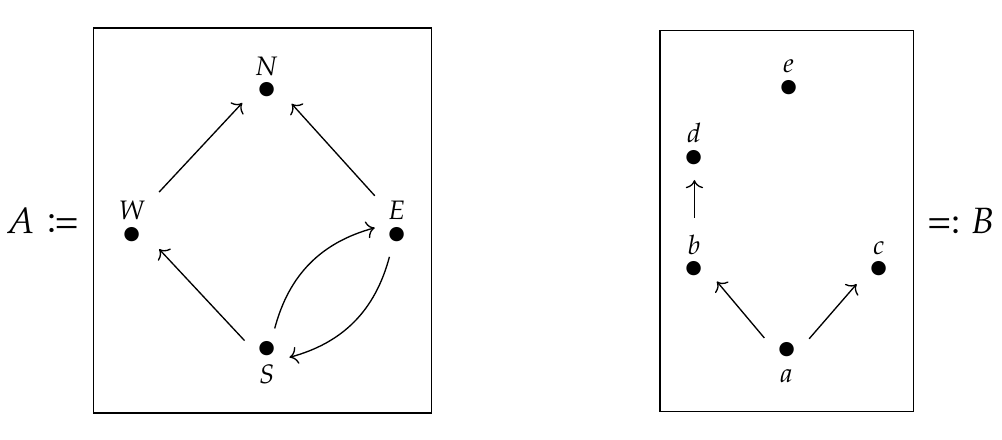
An edge from \(x\) to \(y\) means \(x \le y\), and we can derive other inequalities from these. Similarly, we can draw Lawvere metric spaces using \(\mathbf{Cost}\)-weighted graphs, like these:

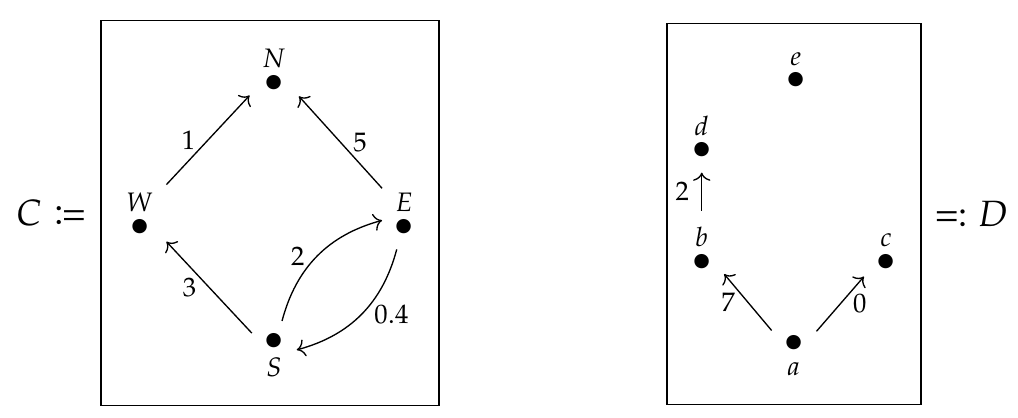
The distance from \(x\) to \(y\) is the length of the shortest directed path from \(x\) to \(y\), or \(\infty\) if no path exists.

All this is old stuff; now we're thinking about enriched profunctors between enriched categories.

A \(\mathbf{Bool}\)-enriched profunctor between \(\mathbf{Bool}\)-enriched categories also called a feasibility relation between preorders, and we can draw one like this:

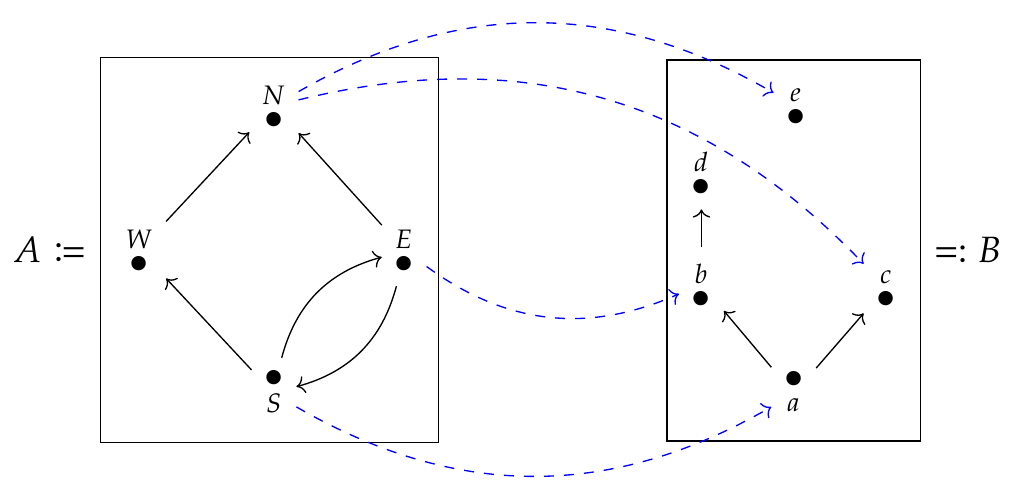
What's a \(\mathbf{Cost}\)-enriched profunctor between \(\mathbf{Cost}\)-enriched categories? It should be no surprise that we can draw one like this:

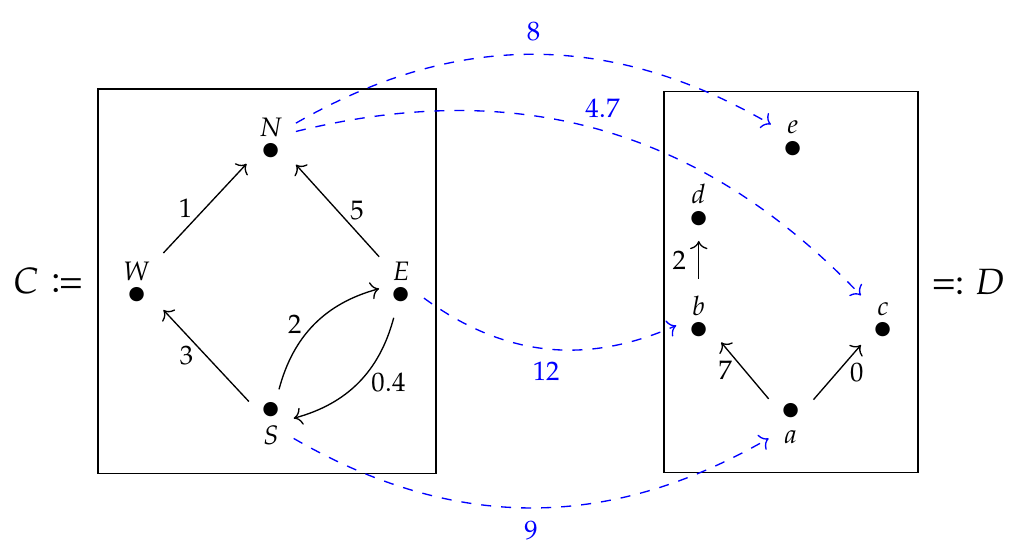
You can think of \(C\) and \(D\) as countries with toll roads between the different cities; then an enriched profunctor \(\Phi : C \nrightarrow D\) gives us the cost of getting from any city \(c \in C\) to any city \(d \in D\). This cost is \(\Phi(c,d) \in \mathbf{Cost}\).

But to specify \(\Phi\), it's enough to specify costs of flights from some cities in \(C\) to some cities in \(D\). That's why we just need to draw a few blue dashed edges labelled with costs. We can use this to work out the cost of going from any city \(c \in C\) to any city \(d \in D\). I hope you can guess how!

Puzzle 182. What's \(\Phi(E,a)\)?

Puzzle 183. What's \(\Phi(W,c)\)?

Puzzle 184. What's \(\Phi(E,c)\)?

Here's a much more challenging puzzle:

Puzzle 185. In general, a \(\mathbf{Cost}\)-enriched profunctor \(\Phi : C \nrightarrow D\) is defined to be a \(\mathbf{Cost}\)-enriched functor

[ \Phi : C^{\text{op}} \times D \to \mathbf{Cost} ]

This is a function that assigns to any \(c \in C\) and \(d \in D\) a cost \(\Phi(c,d)\). However, for this to be a \(\mathbf{Cost}\)-enriched functor we need to make \(\mathbf{Cost}\) into a \(\mathbf{Cost}\)-enriched category! We do this by saying that \(\mathbf{Cost}(x,y)\) equals \( y - x\) if \(y \ge x \), and \(0\) otherwise. We must also make \(C^{\text{op}} \times D\) into a \(\mathbf{Cost}\)-enriched category, which I'll let you figure out to do. Then \(\Phi\) must obey some rules to be a \(\mathbf{Cost}\)-enriched functor. What are these rules? What do they mean concretely in terms of trips between cities?

And here are some easier ones:

Puzzle 186. Are the graphs we used above to describe the preorders \(A\) and \(B\) Hasse diagrams? Why or why not?

Puzzle 187. I said that \(\infty\) plays the same role in \(\textbf{Cost}\) that \(\text{false}\) does in \(\textbf{Bool}\). What exactly is this role?

By the way, people often say \(\mathcal{V}\)-category to mean \(\mathcal{V}\)-enriched category, and \(\mathcal{V}\)-functor to mean \(\mathcal{V}\)-enriched functor, and \(\mathcal{V}\)-profunctor to mean \(\mathcal{V}\)-enriched profunctor. This helps you talk faster and do more math per hour.

To read other lectures go here.

© 2018 John Baez