Lecture 63 - Composing Enriched Profunctors

Now that we've got enriched profunctors up and running, let's see how to compose them! We've already thought about it in some examples. In Lecture 58 we saw how to compose \(\mathbf{Bool}\)-enriched profunctors, also known as feasibility relations:

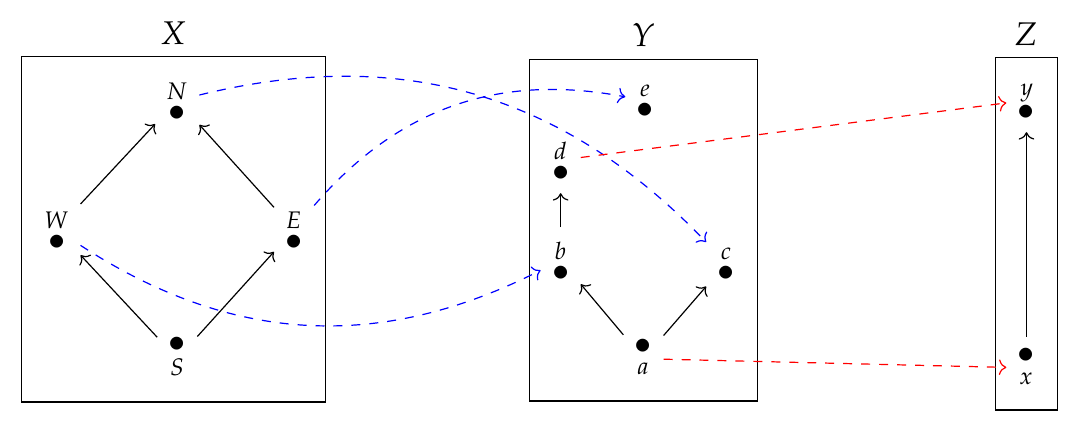
Here we have three \(\mathbf{Bool}\)-enriched categories \(X,Y,\) and \(Z\), also known as preorders, and feasibility relations between these:

[ \Phi \colon X \nrightarrow Y , ] [ \Psi \colon Y \nrightarrow Z. ]

Remember, these are really monotone functions

[ \Phi: X^{\text{op}} \times Y \to \mathbf{Bool} ,] [ \Psi: Y^{\text{op}} \times Z \to \mathbf{Bool}.]

In the pictures \(\Phi(x,y) = \text{true}\) iff there's a path from \(x\in X\) to \(y \in Y\), and \(\Psi(y,z) = \text{true}\) iff there's a path from \(y \in Y\) to \(z \in Z\).

Their composite

[ \Psi\Phi \colon X \nrightarrow Z ]

is given by

[ (\Psi\Phi)(x,z) = \bigvee_{y \in Y} \Phi(x,y) \wedge \Psi(y,z). ]

Remember, the join \( \bigvee \) in \(\mathbf{Bool}\) means 'there exists', while the meet \(\wedge\) means 'and'. So, this formula says that you can get from \(x \in X\) to \(z \in Z\) iff there exists \(y \in Y\) such that you can get from \(x\) to \(y\) and from \(y\) to \(z\).

Now let's generalize this, replacing \(\mathbf{Bool}\) with any sufficiently nice poset \(\mathcal{V}\). Last time we saw that if \(\mathcal{V}\) is a closed commutative monoidal poset we can define \(\mathcal{V}\) -enriched profunctors between \(\mathcal{V}\) -enriched categories. But to compose these enriched profunctors, \(\mathcal{V}\) will need to be a bit nicer.

The reason is not hard to see. Suppose we have three \(\mathcal{V}\)-enriched categories \(\mathcal{X},\mathcal{Y}\), and \(\mathcal{Z}\). Suppose we have \(\mathcal{V}\)-enriched profunctors between these:

[ \Phi : \mathcal{X} \nrightarrow \mathcal{Y}, ] [ \Psi : \mathcal{Y} \nrightarrow \mathcal{Z}. ]

Remember, these are really \(\mathcal{V}\)-enriched functors

[ \Phi \colon \mathcal{X}^{\text{op}} \times \mathcal{Y} \to \mathcal{V} , ] [ \Psi \colon \mathcal{Y}^{\text{op}} \times \mathcal{Z} \to \mathcal{V} . ]

Let's try to compose them using this formula:

[ (\Psi\Phi)(x,z) = \bigvee_{y \in \mathrm{Ob}(\mathcal{Y})} \Phi(x,y) \otimes \Psi(y,z). ]

Note I've replaced the meet \(\wedge\), which is the multiplication in our monoidal poset \(\mathbf{Bool}\), by \(\otimes\), which is the name of the multiplication in a general monoidal poset \(\mathcal{V}\). But I'm keeping the join \(\bigvee\).

Why? The reason is that composing enriched profunctors is like matrix multiplication! First we 'multiply' the matrix entries \(\Phi(x,y)\) and \(\Psi(y,z)\), then we 'sum' over \(y\). The multiplication in \(\mathcal{V}\) is \(\otimes\), but the sum... well, in general a monoidal poset doesn't have a way to do 'sums', but if it has joins then these act like sums!

So, we'd better assume \(\mathcal{V}\) has all joins. There's a name for this:

Definition. A quantale is a closed monoidal poset \( \mathcal{V}\) that has all joins: that is, every subset of \( S\subseteq \mathcal{V}\) has a least upper bound \(\bigvee S\).

'Quantale' may sound like a strange word, but we've seen that posets are good for studying logic, and quantales first showed up in the study of quantum logic. In quantum logic we often need noncommutative quantales, but for our work now we need the multiplication \(\otimes\) in \(\mathcal{V}\) to be commutative.

So, putting it all together:

Definition. If \(\mathcal{V}\) is a commutative quantale and \(\Phi \colon \mathcal{X} \nrightarrow \mathcal{Y}\), \(\Psi\colon \mathcal{Y} \nrightarrow \mathcal{Z}\) are \(\mathcal{V}\)-enriched profunctors, define their composite by

[ (\Psi\Phi)(x,z) = \bigvee_{y \in \mathrm{Ob}(\mathcal{Y})} \Phi(x,y) \otimes \Psi(y,z). ]

Great! But we still need to check that \(\Psi\Phi\) is an enriched profunctor! We've got a well-defined function

[ \Psi\Phi \colon \mathcal{X}^{\text{op}} \times \mathcal{Y} \to \mathcal{V} ]

but we need to check that it's a \(\mathcal{V}\)-enriched profunctor. I'll let you give it a try. This cool fact will help:

Theorem. If \(\mathcal{V}\) is a monoidal poset with all joins, \(\mathcal{V}\) is a quantale if and only if

[ a \otimes \left( \bigvee_{b\in B} b\right) = \bigvee_{b \in A} (a \otimes b) ]

for every element \(a\) and every subset \(B\) of \(\mathcal{V}\).

Proof Sketch. For every element \(a\) of \(\mathcal{V}\) there is a monotone function

[ a \otimes - \, \colon \mathcal{V} \to \mathcal{V} ]

sending each \(x \in \mathcal{V}\) to \(a \otimes x\) . By the Adjoint Functor Theorem for Posets, this monotone function has a right adjoint iff it preserves all joins. It a right adjoint iff \(\mathcal{V}\) is closed, since \(\mathcal{V}\) being closed says that

[ a \otimes x \le y \text{ if and only if } x \le a \multimap y ]

for all \(x, y\) in \(\mathcal{V}\), which means that

[ a \multimap - \, \colon \mathcal{V} \to \mathcal{V} ]

is a right adjoint of

[ a \otimes - \, \colon \mathcal{V} \to \mathcal{V} ]

On the other hand, \(a \otimes -\) preserves all joins iff

[ a \otimes \left( \bigvee_{b\in B} b\right) = \bigvee_{b \in B} (a \otimes b) ]

for every element \(a\) and every subset \(B\) of \(\mathcal{V}\). \( \qquad \blacksquare \)

Now try this puzzle:

Puzzle 198. Suppose \(\mathcal{V}\) is a commutative quantale, and suppose \( \Phi \colon \mathcal{X}^{\text{op}} \times \mathcal{Y} \to \mathcal{V} \) and \( \Psi \colon \mathcal{Y}^{\text{op}} \times \mathcal{Z} \to \mathcal{V} \) are \(\mathcal{V}\)-enriched functors. Show that \( \Psi\Phi \colon \mathcal{X}^{\text{op}} \times \mathcal{Y} \to \mathcal{V} \), defined by

[ (\Psi\Phi)(x,z) = \bigvee_{y \in \mathrm{Ob}(\mathcal{Y})} \Phi(x,y) \otimes \Psi(y,z),]

is a \(\mathcal{V}\)-enriched functor. This means checking an inequality - you can find the definition of enriched functor in Lecture 32.

Also try these:

Puzzle 199. Suppose that \(\mathcal{V}\) is a commutative quantale. Show that composition of \(\mathcal{V}\)-enriched profunctors is associative.

Puzzle 200. Suppose that \(\mathcal{V}\) is a commutative quantale and \(\mathcal{X}\) is a \(\mathcal{V}\)-enriched category. The hom-functor

[ \mathrm{hom} \colon \mathcal{X}^{\text{op}} \times \mathcal{X} \to \mathcal{V} ]

described in Puzzle 197 gives an enriched profunctor that we call \(1_{\mathcal{V}} \colon \mathcal{V} \nrightarrow \mathcal{V}\). Show that this serves as an identity for composition of \(\mathcal{V}\)-enriched profunctors: check the left and right unit laws.

You can see what's coming! If you get stuck I'll help you next time. I'll also give more examples of commutative quantales, and say more about them!

To read other lectures go here.