Lecture 66 - Collaborative Design

Last time we took a peek at a 'co-design diagram':

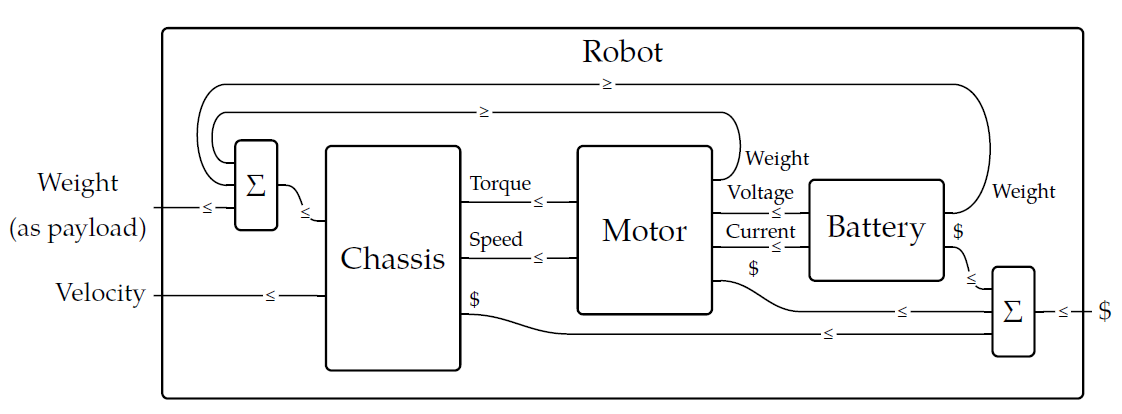
This describes a big complicated feasibility relation built from smaller ones - the little boxes - in various ways. Now let me start explaining those various ways!

First of all, remember that a feasibility relation $\Phi \colon X \nrightarrow Y $ from a preorder $X$ to a preorder $Y$ is monotone function

[ \Phi \colon X^{\text{op}} \times Y \to \lbrace \text{true}, \text{false} \rbrace . ]

In collaborative design we interpret $\Phi(x,y) = \text{true}$ to mean "we can meet the requirements $x$ given the resources $y$". In a codesign diagram we can draw $\Phi$ as a box with one wire coming in at left labelled $X$, and one wire going out at right labelled $Y$:

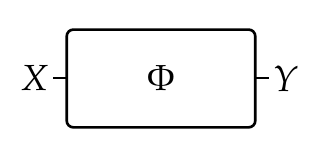
Here are a few easy examples:

Puzzle 204. Suppose you are trying to buy a plane ticket, and the cheapest available ticket is $500. Describe this using a feasibility relation $\Phi : \textbf{Bool} \nrightarrow [0,\infty) $ where we make $ [0,\infty) $, the set of nonnegative real numbers, into a poset with its usual ordering $\le$.

Puzzle 205. Suppose you are trying to buy either one or two loaves of bread - or perhaps none. Suppose bread costs $2 per loaf. Describe this using a feasibility relation $\Psi : \lbrace 0,1,2\rbrace \nrightarrow [0,\infty) $. Here we make $ {0,1,2}$ into a poset with its usual ordering.

Puzzle 206. Suppose you are trying to feed hungry children with the loaves of bread you bought in the previous puzzle, and you can feed at most three children with each loaf of bread. Describe this using a feasibility relation $\Phi : \mathbb{N} \nrightarrow \lbrace 0,1,2\rbrace $. Here $\mathbb{N}$ is the set of natural numbers $ \lbrace 0,1,2,3,\dots \rbrace $ with its usual ordering.

Second, remember from Lecture 58 that we can compose feasibility relations $\Phi \colon X \nrightarrow Y$ and $\Psi \colon Y \nrightarrow Z$ to get a feasibility relation $\Psi \Phi \colon X \nrightarrow Z$. We draw this as follows:

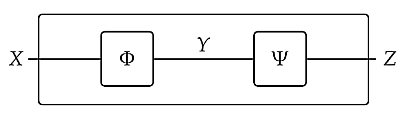
The box on the outside helps us think of $\Psi\Phi$ as a single thing, but we could also leave it out.

The idea in codesign is that this describes two systems or processes stuck together, with the second providing the resources required for the first. Let's look at an easy example:

Puzzle 207. Suppose you buy loaves of bread and then use them to feed hungry children. Compose the feasibility relation $\Psi : {0,1,2} \nrightarrow [0,\infty) $ from Puzzle 205 and the feasibility relation $\Phi : \mathbb{N} \nrightarrow \lbrace 0,1,2\rbrace $ from Puzzle 206 to get a feasibility relation $\Psi \Phi : \mathbb{N} \nrightarrow [0,\infty) $ describing how many children you can feed for a certain amount of money (given the fact that you plan to buy at most two loaves).

Third, if we have a bunch of preorders $X_1, \dots, X_m $ and $Y_1, \dots, Y_n$, their products $X_1 \times \cdots \times X_m$ and $Y_1 \times \cdots \times Y_n $ are also preorders, so we can talk about a feasibility relation

[ \Phi \colon X_1 \times \cdots \times X_m \nrightarrow Y_1 \times \cdots \times Y_n ]

We draw this as a box with a bunch of wires going in and a bunch going out, as follows:

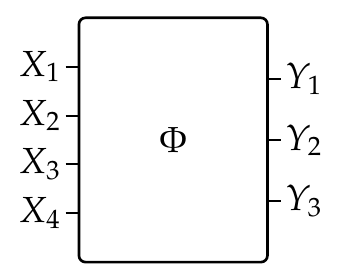
The idea in codesign is that this describes a situation where a bunch of resources $Y_1, \dots, Y_n$ are needed to meet a bunch of requirements $X_1, \dots, X_m$.

Puzzle 208. Suppose you some slices of bread, some slices of cheese and some slices of ham. You are trying to make sandwiches. You can make a cheese sandwich with two slices of bread and one slice of cheese. You can make a ham sandwich with two slices of bread and one slice of ham. There is a feasibility relation $\Theta : \mathbb{N} \times \mathbb{N} \nrightarrow \mathbb{N} \times \mathbb{N} \times \mathbb{N} $ where $\Theta(m,n,i,j,k) = \text{true}$ if you can make $m$ cheese sandwiches and $n$ ham sandwiches from $i$ slices of bread, $j$ slices of cheese and $k$ slices of ham.

Fourth, if we have feasibility relations $\Phi \colon X \nrightarrow Y$ and $\Psi \colon X' \nrightarrow Y'$, we can define a new feasibility relation

[ \Phi \otimes \Psi \colon X \times X' \nrightarrow Y \times Y' ]

given by

[ (\Phi \otimes \Psi)((x,x'),(y,y')) = \Phi(x,y) \wedge \Psi(x',y') ]

We call this way of combining feasibility relations tensoring, and we draw $\Phi \otimes \Psi$ as follows:

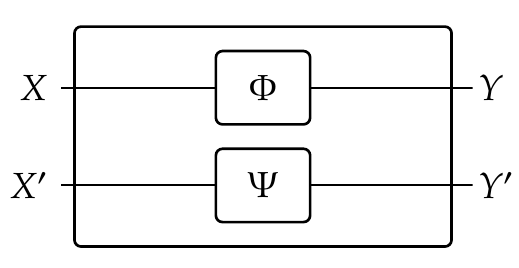
This describes a situation where we can meet the requirements $(x,x')$ given resources $ (y,y') $ iff we can meet requirement $x$ given $x'$ and meet requirement $y$ given $y'$.

Here is a very simple example:

Puzzle 209. Suppose you are trying to fry some eggs and also toast some slices of bread. Describe each process separately as a feasibility relation from $\mathbb{N}$ to $\mathbb{N}$ and then tensor these relations. What is the result?

Puzzle 210. Show that $\Phi \otimes \Psi$ is really a feasibility relation if $\Phi$ and $\Psi$ are feasibility relations.

Puzzle 211. What general mathematical result is Puzzle 209 an example of?

Puzzle 212. We can get a feasibility relation by taking either the companion or the conjoint of a monotone map, thanks to the ideas in the puzzles of Lecture 65. Which of the feasibility relations in this lecture's puzzles are companions or conjoints?

To read other lectures go here.