

This is a 'cross fox': a red fox with some melanistic traits.
April 4, 2020

I stand up for all downtrodden, oppressed mathematical objects. Consider the humble commutative semigroup. This is a set with a binary operation \(+\) obeying $$ x+y=y+x $$ and $$ (x+y)+z = x+(y+z) $$ for all elements \(x,y,z\). Too simple for any interesting theorems? No!
We can describe commutative semigroups using generators and relations. I'm especially interested in the finitely presented ones.
We can't hope to classify all commutative semigroups, not even the finitely presented ones. But there's plenty to say about them. n
For starters, some examples. Take any set of natural numbers. If you take all finite sums of these you get a commutative semigroup. So here's a finitely generated one: $$ \{5,7,10,12,14,15,17,19,20,21,22,\dots \} $$
See the generators? This kind of example is called a numerical semigroup, although by convention people decree that \(0\) must be an element of any numerical semigroup, since if it's not you can always put it in without changing anything else.
We can also put in extra relations. So there's a commutative semigroup like this: $$ \{5,7,10,12,14,15,17,19,20,21,22 \} $$ with addition as usual except if you'd overshoot \(22\) you decree the sum to be \(22\), e.g. \(21+5=22\).
Now it's time to bring a bit of order to this wilderness! Given any commutative semigroup \(C\) we can impose the relations \(a+a=a\) for all \(a\). The result is called a semilattice. Let's call it \(C'\). There's a homomorphism $$ p\colon C \to C' $$ Note that if \(p(x) = a\) and \(p(y) = a\) then $$ p(x+y) = a+a = a $$ So the set of \(x\) in \(C\) that map to a given element \(a\) in the semilattice \(C'\) is closed under addition! It's a sub-semigroup of \(C\).
In short, given a commutative semigroup C it maps onto a semilattice $$ p\colon C \to C' $$ and each 'fiber' $$ \{x: p(x) = a\} $$ is a commutative semigroup in its own right.
And these fibers are especially nice: they're 'archimedean semigroups'. A semigroup is archimedean if it's commutative and for any \(x,y\) we have $$ x+ \cdots +x = y+z $$ for some \(z\) and some number of times of adding \(x\). Can you guess why this property is called 'archimedean'? Hint: it's true for the positive real numbers!
I'll let you check that the fibers of the map from a commutative semigroup \(C\) to its semilattice \(C'\) are archimedean. It's a fun way to pass the time when you're locked down trying to avoid coronavirus. So, people say "any commutative semigroup is a semilattice of archimedean semigroups".
So, to a large extent we've reduced the classification of commutative semigroups to two cases:
Semilattices are nice because they always have a partial order \(\le\) where \(a+b\) is the least upper bound of \(a\) and \(b\). Archimedean semigroups are a different story. For example, every abelian group is archimedean.
To see how the story continues, go to this great post:

In spherical geometry, the parallel postulate breaks down.
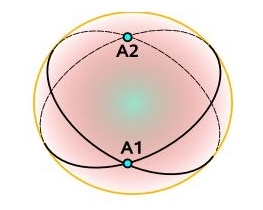
Spherical trigonometry is more beautiful than plane trigonometry because the sides of a triangle are also described by angles!
This spherical triangle has 3 angles \(A,B,C\) and 3 sides, whose lengths are conveniently described using the angles \(a,b,c\):

You can see this beautiful symmetry in the 'law of sines': $$ \frac{\sin A}{\sin a} = \frac{\sin B}{\sin b} = \frac{\sin C}{\sin c} $$ Here \(A,B,C\) are the angles of a spherical triangle and \(a,b,c\) are the sides, measured as angles. Or the other way around: it's still true if we switch \(A,B,C\) and \(a,b,c\)!
Spherical geometry is also beautiful because it contains Euclidean geometry. Just take the limit where your shape gets very small compared to the sphere!
For example, if the sides \(a,b,c\) of a spherical triangle become smaller and smaller, $$\frac{\sin a}{a}, \frac{\sin a}{b}, \frac{\sin c}{c} \to 1$$ so we get the familiar law of sines in Eucliean geometry: $$ \frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c} $$ The law of cosines in spherical geometry is more complicated: $$ \cos a = \cos b \, \cos c + \sin b \, \sin c \, \cos A $$ $$ \cos b = \cos c \, \cos a + \sin c \, \sin a \, \cos B $$ $$ \cos c = \cos a \, \cos b + \sin a \, \sin b \, \cos C $$ But you can use it to prove the law of sines. And you just need to remember one of these 3 equations.
Puzzle. In the limit where \(a,b,c \to 0\) show the spherical laws of cosines gives the usual Euclidean rule of cosines.
In 100 AD the Greek mathematician Menelaus of Alexandria wrote a 3-volume book Sphaerica that laid down the foundations of spherical geometry. He proved a theorem with no planar analogue: two spherical triangles with the same angles are congruent! And much more.
Menelaus' book was later translated into Arabic. In the Middle Ages, astronomers used his results to determine holy days on the Islamic calendar. In the 13th century, Nasir al-Din al-Tusi discovered the law of sines in spherical trigonometry!
Later mathematicians discovered many other rules in spherical trigonometry. For example, these additional laws: $$ \cos A = -\cos B \, \cos C + \sin B \, \sin C \, \cos a $$ $$ \cos B = -\cos C \, \cos A + \sin C \, \sin A \, \cos b $$ $$ \cos C = -\cos A \, \cos B + \sin A \, \sin B \, \cos c $$
So in what sense did people only 'invent non-Euclidean geometry' in the 1800s?
Maybe this: to get the axioms of Euclidean geometry except for the parallel postulate to apply to spherical geometry, we need to decree that opposite points on the sphere count as the same. Then distinct lines intersect in at most one point!
Or maybe just this: people were so convinced that the axioms of Eucidean geometry described the geometry of the plane that they wouldn't look to the sky for a nonstandard model of these axioms.
Geometry where we identify opposite points on the sphere is called 'elliptic geometry':
Spherical trigonometry is full of fun stuff, and you can learn about it here:
Most mathematicians are not writing for people. They're writing for
God the Mathematician. And they're hoping God will give them a pat on
the back and say "yes, that's exactly how I think about it".
April 12, 2020
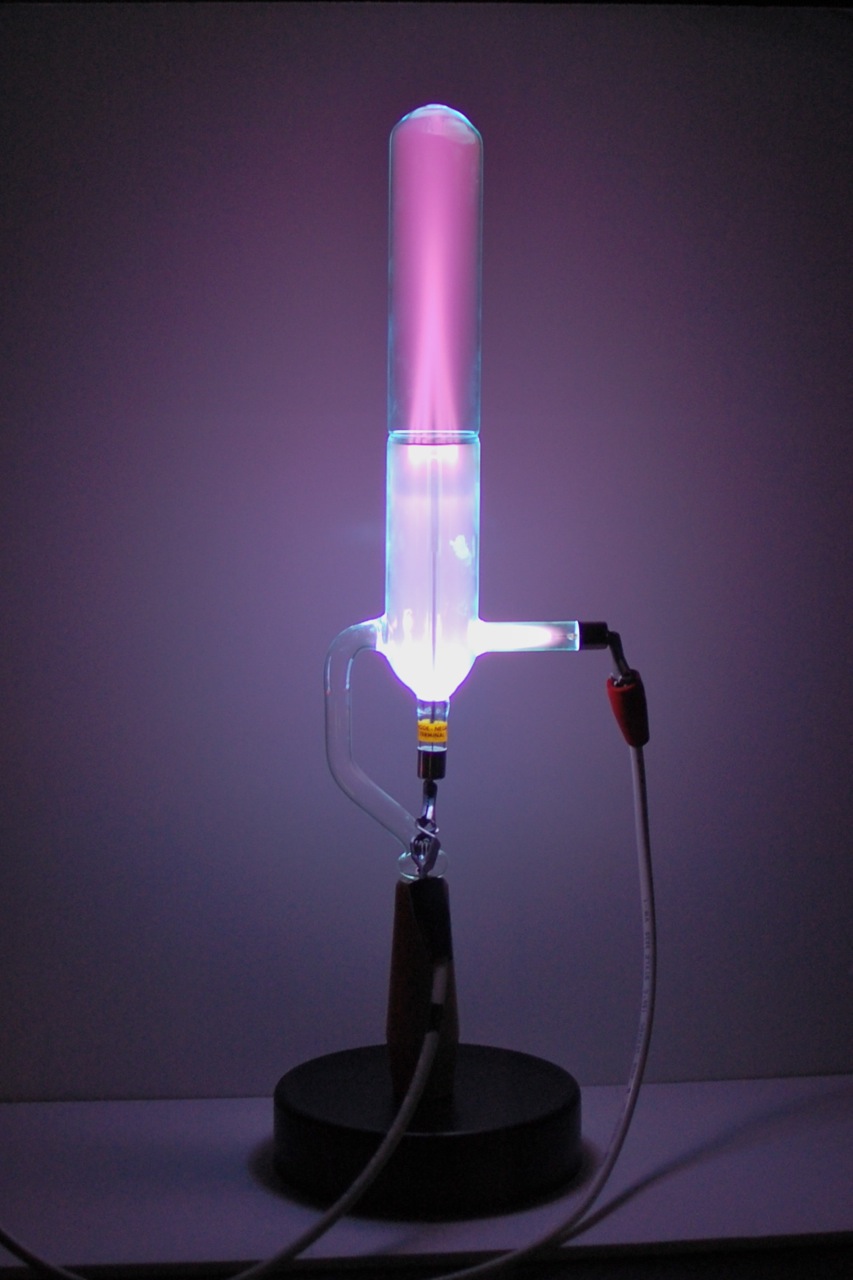
Back in 1886, you didn't need an enormous particle accelerator to discover new particles. You could build a gadget like this and see faint rays emanating from the positively charged metal tip.
They called them 'canal rays'. They also called them 'anode rays', since a positively charged metal tip is called an 'anode'.
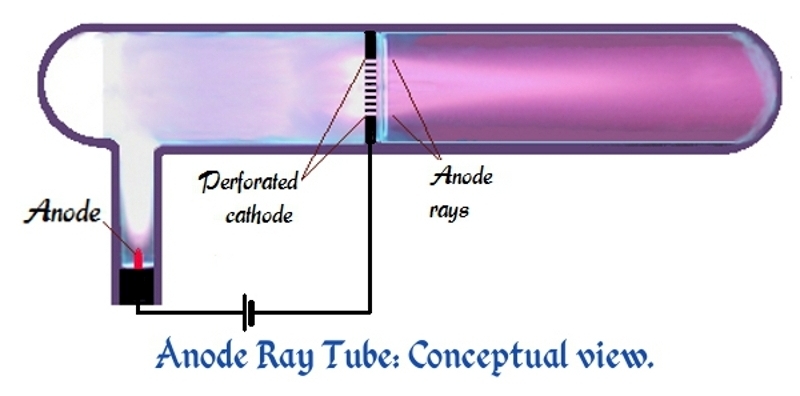
We now know these anode rays are atoms that have some electrons stripped off, also known as 'positively charged ions'. So, they come in different kinds!
But back in 1886 when Goldstein discovered them, it wasn't clear whether canal rays were particles or just 'rays' of some mysterious sort. 'Cathode rays', now known to be electrons, had already been discovered in 1876.
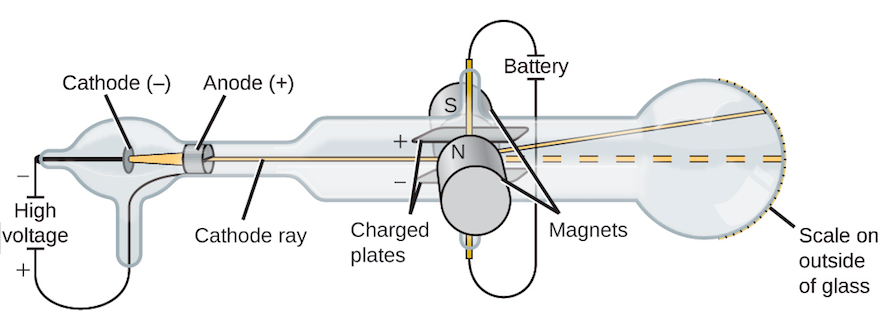
X-rays (now known to be energetic photons) came later, in 1895.
Lots of rays! And there were also 'N-rays', now known to be a mistake.
I love the complicated story of how people studied these various 'rays' and discovered that atoms were electrons orbiting atomic nuclei made of protons and neutrons... and that light itself is made of photons.
These were the glory days of physics — the wild west.
To learn more about these stories, I recommend the start of this:

In the late 1800s, when physicists were trying to understand how stable atoms of different kinds could exist, Tait's experiments with smoke rings seemed quite exciting. They're quite stable. So people thought: maybe atoms are vortices in the 'aether' — the substance filling all space, whose vibrations were supposed to explain electromagnetism!
To explain different kinds of atoms, Tait suggested they were knotted or linked vortex rings. He classified knots to see if this could explain the atoms we see. And thus knot theory was born!
Later Kelvin became fascinated by the theory of vortex atoms. He begain studying vortex rings, using ideas developed by Helmholtz starting around 1858.
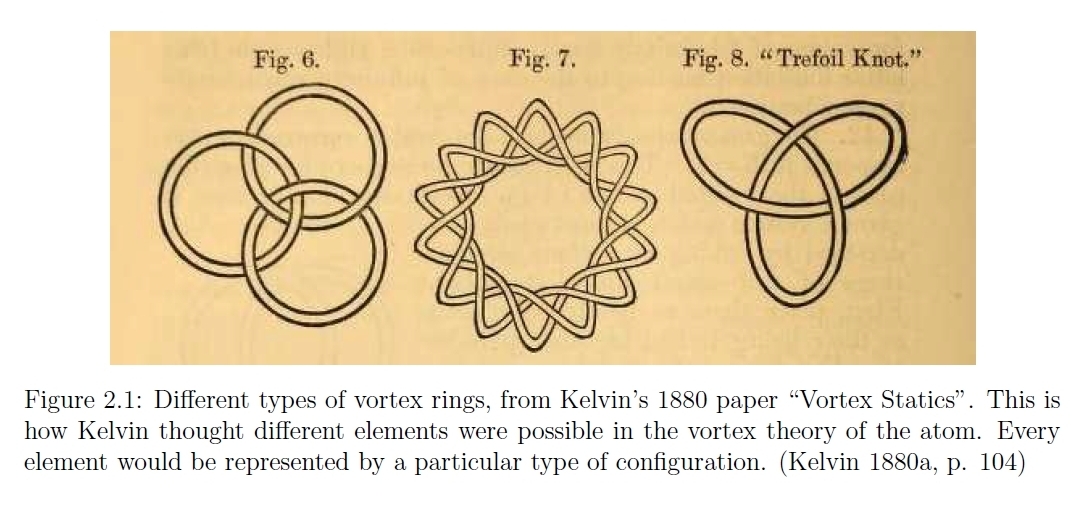
Kelvin (= Thomson) argued that vortex rings were a better theory than the main alternative: atoms as point particles or infinitely rigid balls. He started calculating the vibrational modes of vortex rings, hoping they could explain atomic spectra!

For a while, in the late 1800s, you could get a job at a British university studying vortex atoms. The subject was never very popular outside Great Britain.

Over time the models became more complex, but they never fit the behavior of real-world atoms with any precision. Eventually Kelvin gave up on vortex atoms... but he didn't admit it publicly until much later.
In an 1896 talk FitzGerald, another expert on vortex atoms, recognized the problems — but argued that it was "almost impossible" to falsify the theory, because it was so flexible.

The theory of vortex atoms was never quite disproved. But eventually people lost interest in them — thanks in part to rise of Maxwell's equations (which led to other theories of atoms), and later perhaps in part to the discovery of electrons, and "canal rays", and other clues that would eventually help us unravel the mystery of atoms.
All the quotes above are from this wonderful article:
Read it and you'll be transported to a bygone age... with some lessons for the present, perhaps.
Jim Baggott also recommends this:
The French mathematicians who went under the pseudonym Nicolas Bourbaki did a lot of good things - but not so much in the foundations of mathematics. Adrian Mathias, a student of John Conway, showed their definition of "1" would be incredibly long, written out in full.
One reason is that their definition of the number 1 is complicated in the first place. Here it is. I don't understand it. Do you?
But worse, they don't take \(\exists\), "there exists", as primitive. Instead they define it—in a truly wretched way.
They use a version of Hilbert's "choice operator". For any formula \(\Phi(x)\) they define a quantity that's a choice of \(x\) making \(\Phi(x)\) true if such an choice exists, and just anything otherwise. Then they define \(\exists x \Phi(x)\) to mean \(\Phi\) holds for this choice.
This builds the axiom of choice into the definition of \(\exists\) and \(\forall\). Worse, their implementation of this idea leads to huge formulas.
And in the 1970 edition, things got much worse!
You can read Mathias' paper here:
At least that's what a calculation by the logician Robert Solovay showed. But the details of that calculation are lost. So I asked around. I asked Robert Solovay, who is retired now, and he said he would redo the calculation.
I asked on MathOverflow, and was surprised to find my question harshly attacked. I was accused of "ranting". Someone said the style of my question was "awful".
Maybe they thought I was attacking Bourbaki. That's not my real goal here. I'm thinking of writing a book about large numbers, so I'm doing a bit of research.
Admittedly, I added the remark saying Mathias' paper is "polemical" after Todd Trimble, a moderator at MathOverflow, recommended doing some such thing.
Later Solovay said it would be hard to redo his calculation — and if he did he'd probably get a different answer, because there are different ways to make the definition precise.
But here's some good news. José Grimm redid the calculation. He did it twice, and got two different answers, both bigger than Solovay's. According to these results Bourbaki's definition of "1", written on paper, may be 400 billion times heavier than the Milky Way.
I'm now quite convinced that a full proof of \(1+1=2\) in Bourbaki's formalism, written on paper, would require more atoms than available in the observable Universe.
Of course, they weren't aiming for efficiency.
April 17, 2020
Some news:
I was able to reproduce Mathias's [actually Solovay's] results with some Haskell code with some specific details about how many symbols are needed in each term. (As a sanity check, I verified I recovered the same results term-by-term when the ordered product was primitive.)
- Size of 1 = 2,409,875,496,393,137,472,149,767,527,877,436,912,979,508,338,752,092,897
- Size of term A = 15,756,227
- Size of term B = 10,006,221,599,868,316,846
- Size of term C = 59,308,566,315
- Size of term D = 364,936,653,508,895,574,881
- Size of term E = 101,217,516,631
One thing worth noting is that, well, this seems dishonest. I mean, there are a lot of double negations which are not simplified, which bloats the size quite a bit (an additional \(1.863 \times 10^{53}\) symbols or so). I wouldn't be surprised if there were other simplifications which would cut down the bloat further...not that we'd get anything less than \(10^{50}\) or so.
If you'd like to check the number of links, I can do that too.
He writes:
Addendum. The relation "1+1=2" can be computed, and found to have a length of $$ 22,411,322,875,029,037,193,545,441,224,646,148,573,589,725,893,763,139,344,694,162,029,240,084,343,041 $$ or approximately $$ 2.24113228750290371 \times 10^{76}. $$ This is using the definitions in Bourbaki of cardinal addition \( \mathfrak{a}+\mathfrak{b}\) using the disjoint sum of the indexed family \( f\colon\mathrm{Card}(2)\to \{\mathfrak{a},\mathfrak{b}\}\) considered as a graph. It's really convoluted, but the details can be found in Bourbaki's Theory of Sets Chapter II sections 3.4, 4.1, and 4.8 as well as Proposition 5 (in chapter III, section 3.3); this all works with the Kuratowski ordered pair, not a primitive \(\bullet A B\) ordered pair.For what it's worth, computing the size of 1 was nearly instantaneous, whereas computing the size of "1+1=2" took about 7 minutes and 30 seconds.
This is a private document [for the eyes of RMS and ARDM only] which extends ARDM's computation of the length of the Bourbaki rendition of "The ineffable name of 1" to the case when the Kuratowski ordered pair is employed. My plan is to write programs in Allegro Common Lisp to compute the relevant numbers.I program using the style of "literate programming" introduced by Knuth. However the Web and Tangle introduced by Knuth [which have been refined to CWEb and CTangle by Levy] are limited to languages closely linked to C or Pascal. So I prefer to use a more flexible literate programming language which permits fairly arbitrary target languages. Currently, I use Nuweb which is available on the TEX archives in the directory /web/nuweb.
One of the nice things about literate programming is that one can write programs in the natural psychological order, but arrange that the output files have the order needed for the target programming language. We will exploit this heavily in what follows.
From solovay@math.berkeley.edu Wed Nov 11 13:39:46 1998
Date: Tue, 10 Nov 1998 23:43:04 -0800 (PST)
From: "Robert M. Solovay"
To: amathias@rasputin.uniandes.edu.co
Cc: solovay@math.berkeley.edu
Subject: Results
Adrian,
Here is the printout of my calculation of the length of the
Bourbaki term for 1. If we do the original definition, I get approx.
4.524 * 10^{12}
If we use the Kuratowski ordered pair, I get approx.
2.41 * 10^{54}
This is big, but not nearly as big as the 2 * 10^{73} that you
claim. This is certainly related to the smaller estimate that I have
for the size of the Kuratowski ordered pair.
I omitted some trivial lines from this printout where I "gave
the wrong commands to the genie".
USER(1): (setq p 0) ;;;[Doing the original Bourbaki definition where
;;; ordered pair is a basic undefined notion.]
0
USER(3): (load "compute.cl")
; Loading ./compute.cl
T
USER(4): J_length
4523659424929
USER(5): (log J_length 10)
12.65549
USER(6): J_links
1179618517981
USER(7): (log J_links 10)
12.071742
USER(8): (setq p 1) ;;; Now use Kuratowski ordered pair
1
USER(10): (load "compute.cl")
; Loading ./compute.cl
T
USER(11): J_length
2409875496393137472149767527877436912979508338752092897
USER(12): (log J_length 10)
54.381996
USER(13): J_links
871880233733949069946182804910912227472430953034182177
USER(14): (log J_links 10)
53.940456

This is a yellow-bellied three-toed skink.
Near the coast of eastern Australia, it lays eggs. But up in the mountains, the same species gives birth to live young! Intermediate populations lay eggs that take only a short time to hatch.
Even more surprisingly, Dr. Camilla Whittington found a yellow-bellied three-toed skink that lay three eggs and then weeks later, give birth to a live baby from the same pregnancy!

(Here, alas, she is holding a different species of skink.)
The yellow-bellied three-toed skink may give us clues about how and why some animals transitioned from egg-laying (ovipary) to live birth (vivipary). I wish I knew more details!
Its Latin name is Saiphos equalis. It's the only species of its genus.

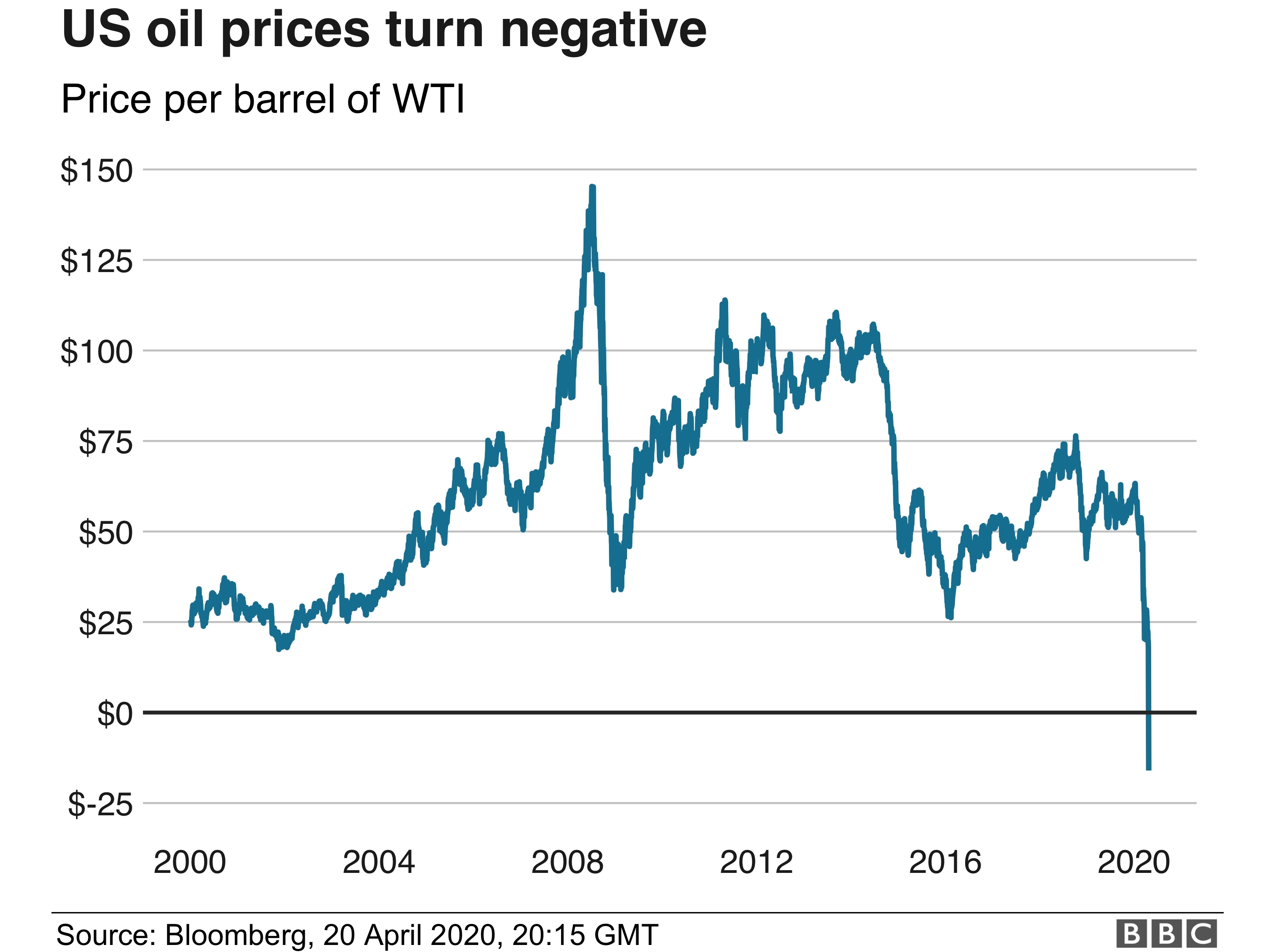
I predict that next week the price of oil will hit negative infinity,
then start coming down from positive infinity, then take a left turn
and develop a positive imaginary part.
April 24, 2020
Funny how it works. Learning condensed matter physics led me to the
'10-fold way' and 'super division algebras'.
That made me want to learn more about division algebras over fields other than the real numbers!
Now I'm studying generalizations of the quaternions.

Here's a great little introduction to quaternion algebras:
Category theorists ask: "What's this an example of?"
I'm in that situation myself trying to learn about division algebras and how they're connected to Galois theory. Gille and Szamuely's book Central Simple Algebras and Galois Cohomology is a great introduction.
But one of the key ideas, 'Galois descent', was explained in a way that was hard for me to understand.
It was hard because I sensed a beautiful general construction buried under distracting details. Like a skier buried under an avalanche, I wanted to dig it out.
I started digging, and soon saw the outlines of the body. We have a field \(k\) and a Galois extension \(K\). We have the category of algebras over \(k\), \(\mathrm{Alg}(k)\), and the category of algebras over \(K\), \(\mathrm{Alg}(K)\). There is a functor $$ F \colon \mathrm{Alg}(k) \to \mathrm{Alg}(K) $$ which is a left adjoint.
We fix \(A \in \mathrm{Alg}(K)\). We want to classify, up to isomorphism, all \(a \in \mathrm{Alg}(k)\) such that \(F(a) \cong A\). This is the problem!
The answer is: the set of isomorphism classes of such \(a\) is $$ H^1(\mathrm{Gal}(K|k), \mathrm{Aut}(A)) $$ This is the first cohomology of the Galois group \(\mathrm{Gal}(K|k)\) with coefficients in the group \(\mathrm{Aut}(A)\), on which it acts.
I began abstracting away some of the details. My first attempt is here:
But last night, I found Qiaochu Yuan wrote a series of articles tackling exactly this problem: finding a clean categorical understanding of Galois descent! He was tuned into exactly my wavelength.
This is where the series starts:
\(\mathrm{Gal}(K|k)\) doesn't act on any one object of \(\mathrm{Alg}(K)\), since Galois transformations aren't \(K\)-linear. It acts on the whole category \(\mathrm{Alg}(K)\)!
The third in his series corrects a mistake. The fourth shows that objects of \(\mathrm{Alg}(k)\) are the same as homotopy fixed points of the action of \(\mathrm{Gal}(K|k)\) on \(\mathrm{Alg}(K)\):
I've loved homotopy fixed points of group actions on categories for years! They're such a nice generalization of the ordinary concept of 'fixed point'.
With this background, Qiaochu is able to state the problem of Galois descent in a clear and general way, which handles lots of other problems besides than the one I've been talking about:
For one, group cohomology has a strong connection to topology. I explained this in the case of \(H^1\) in a comment on the n-Category Café. Since Galois extensions of fields are analogous to covering spaces in topology, this should give us extra insight into Galois descent!
So I have some more fun thinking to do, despite the enormous boost provided by Qiaochu Yuan.
By the way, I'm sure some experts in algebraic geometry already have the categorical/topological perspective I'm seeking. This is not new research yet: this is study.