

This spring I learned that most of the weeds in our yard are edible — and delicious. We don't have weeds. We have salad!
Growing your own arugula: it's not rocket science.
When it rains, which happens only in the winter and spring, we get a
lot of Australian rocket (Sisymbrium erysimoides), wild lettuce
(Lactuca virosa), sow thistle (Sonchus arvensis),
prickly sow thistle (Sonchus asper) and wild turnip, a kind of
mustard (Brassica rapa sylvestris).
May 2, 2020
There are three finite-dimensional associative division algebras over
the real numbers: finite-dimensional real vector spaces equipped with
an associative product where you can divide by anything nonzero!
You can see this by taking tensor products of \(\mathbb{R}\), \(\mathbb{C}\), and \(\mathbb{H}\). A tensor product of two real vector spaces is a new real vector space whose dimension is the product of their dimensions. You can make the tensor product of algebras over the real numbers into another algebra over the reals!
Let's try it. Here are some boring examples:
But let's do some more interesting examples....
Note how \(\mathbb{C}\) 'eats' everything else and makes it complex. It's not in the Brauer group!
In short, the Brauer group of the real numbers has two elements. The complex numbers is not allowed into this group because it eats everything you tensor it with. Turns out that's because it's not just a division algebra, it's a field: it's commutative!
You can do this 'Brauer group' game starting with any field. There are associative division algebras over this field. You can tensor them, and figure out a multiplication table. Some will have inverses, and they're in the Brauer group!
The Brauer group of the rational numbers, \(\mathbb{Q}\), is a lot more interesting than the Brauer group of \(\mathbb{R}\).
Brauer, Hasse and Noether teamed up and figured out the Brauer group of any 'algebraic number field', meaning \(\mathbb{Q}\) with some algebraic numbers like \(\sqrt{-2}\) and \(\sqrt[3]{7}\) thrown in.

Here's a really fun way to learn more about this:
It's fun to read the first letter from Noether to Brauer on this subject in 1927. She is quite dominant! But it makes sense: Brauer was younger, and he had sent her his thesis for comments just earlier that year.

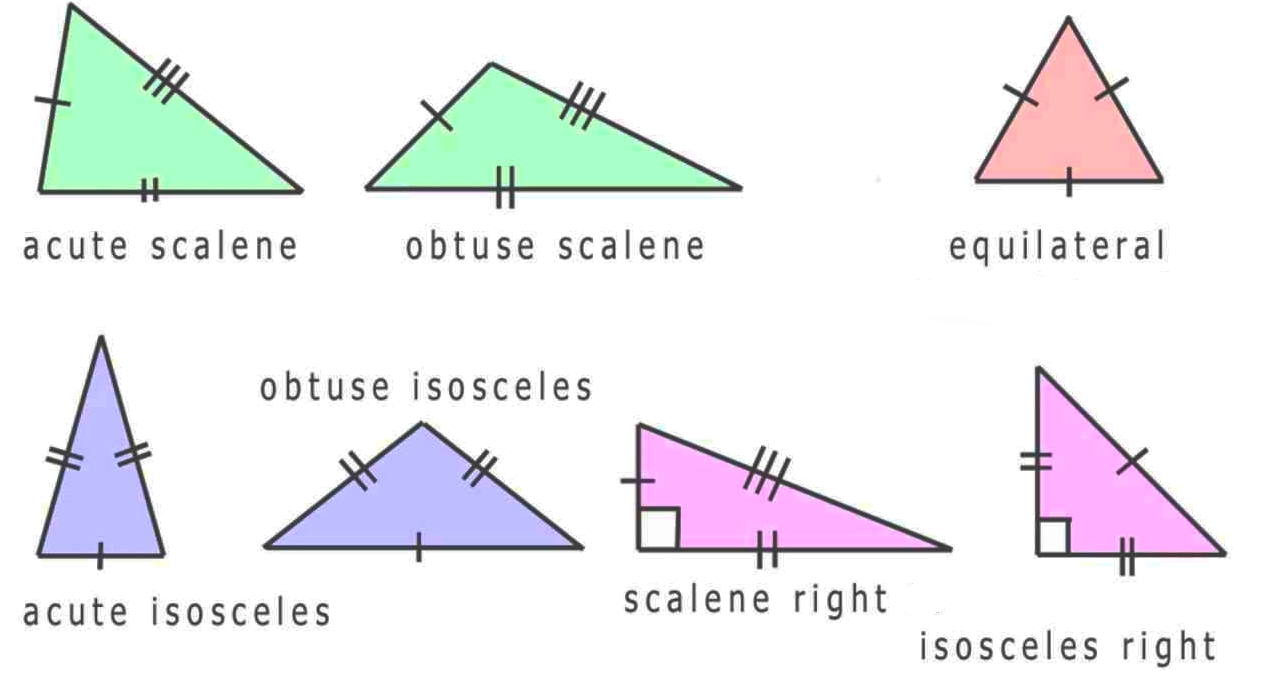
Triangles with symmetries — isosceles and equilateral — have morphisms to themselves.
This category is a 'groupoid': all morphisms have inverses.
In fact it's a 'Lie groupoid': there's a smooth manifold of objects, a smooth manifold of morphisms, and composition is a smooth function. (There's a bit more to the definition, but that's most of it.)
Any Lie groupoid gives a 'differentiable stack'. I won't define those, but the advantage of working with stacks is that the morphisms are more flexible. Only when you move on up to differentiable stacks are you combining groupoids & manifolds in the best way!
Differentiable stacks tend to be good when you've got a space of things with symmetries — like the space of all triangles in the plane. As a thing moves around in this space, its amount of symmetry can suddenly increase, like when a scalene triangle become isosceles.
The 'moduli space' — the space of isomorphism classes of things — will have singularities at the points where those things have more symmetry. But the differentiable stack will still be nice there, because you're not modding out by those symmetries.
Stacks are still scary to most mathematicians. The Stacks Project aims at becoming a complete reference on stacks as used in algebraic geometry:
But differentiable stacks are something you've already met in school, without knowing it! For a detailed introduction to stacks, with a lot about the stack of triangles, try this:


Like many scientists I have a grudging admiration for the Star Trek franchise: grudging because the science is so often silly, and could often have been improved easily without spoiling the stories; admiration because they've created a hopeful vision of the future, some fun stories, and some enduringly interesting characters. In Discovery we heard about the Logic Extremists, a dissident faction of Vulcans who wanted to leave the Federation. But we didn't learn much about their core beliefs! They seemed rather similar to the Vulcan Isolationists, who came about a hundred years later. There seemed to be an interesting untold story lurking behind the name.
So, I went to T'Karath and spent a couple of weeks poring through the historical documents on this movement. Here's a quick sketch of what I found.
In the first half of the 22nd century, the central government had become corrupt, with Romulan operatives infiltrating the Vulcan High Command. Some Vulcans, the Syrannites, attempted to reinstate and develop the original teachings of the Vulcan philosopher Surak. But around 2140, another small group decided that Surak had not developed logic with sufficient thoroughness. They argued that all deductive reasoning should be formalized, all inductive reasoning should be Bayesian with explicit probabilities on hypotheses, and all decision-making should maximize utility.
The Pure Logic movement, as they called themselves, moved to Xir'tan and set up a commune there. They began a program of formal concept analysis so that all words would have precise definitions. Before each meal they bowed, seemingly in prayer, but actually to optimize their activities to come. Children were schooled in an even more disciplined way than usual: less high-tech than the skill domes of the 2200s, but with an intense focus on logic, semiotics, probability, and statistics.
Conflicts erupted in 2200 between what we would call Jaynesian-Bayesians and hardcore subjective Bayesians. The former advocated entropy-maximizing priors. The latter argued that no prior counts as 'right' without further assumptions, so one can start with any prior.
As the Pure Logic movement became established, they spread and set up communes the main continent, especially in Gol, Xial and Raal. They started influencing the political establishment, first locally and then at the federal level.
As this happened, factions with radical positions gradually gained influence. Especially important were the subjective Bayesians who argued that ethics could not be logically derived, so that instead of maximizing utility, a rational agent was free to maximize any chosen quantity. Their motto was remarkably similar to a saying credited to Hume:
Going further, the most extreme subjective Bayesians adopted spreading the Pure Logic movement as their only goal. All decisions were to be evaluated based on how much they furthered the spread of logical thinking. They took a vow to this effect, and pressed this vow on other citizens as a prerequisite for holding office of any sort. Their opponents dubbed them "Logic Extremists".
In 2226, in a hard-fought political struggle, these extremists triumphed and completely pushed the Jaynesian-Bayesians and moderate subjective Bayesians out of power. Two years later V'arak took control: a charismatic leader who asserted with 100% prior probability that the Federation was trying to subvert Vulcan culture and stop the spread of the Pure Logic movement.
Any attempt to reason with V'arak and his supporters, or compromise with them, was interpreted as further evidence of an increasingly elaborate Federation conspiracy. Most Vulcans repudiated this stance, and as the Logic Extremists' public support shrank they turned to terrorism.
The violence came to a head around 2256, when V'latak (shown below) attempted to assassinate Sarek before the peace talks on Cancri IV, saying:
At this point support for the Logic Extremists rapidly dropped, though Patar still managed to infiltrate Section 31.
However, the most interesting aspect of the Logic Extremists are their
early theoretical writings — especially those of Avarak, and Patar's
father Tesov. They were an extremely bold attempt to plan a society
based purely on logic. I hope they're translated soon.
May 14, 2020
I've been thinking about Morita equivalence.
The basic idea is this: any ring has a category of modules. If two rings have equivalent categories of modules, they're 'Morita equivalent'. So we take the attitude: "the main reason to care about rings is their modules".
Isomorphic rings are Morita equivalent, but the fun part is that nonisomorphic rings can be Morita equivalent! For example, the ring of \(n\times n\) matrices with entries in a ring \(R\) is Morita equivalent to \(R\), since a module of this matrix ring must look like \(M^n\) for some module \(M\) of \(R\).
Lots of properties of rings are invariant under Morita equivalence. For example, if two rings are Morita equivalent, and one of them is 'simple' (has no nontrivial ideals), then so is the other.
But the property of being commutative isn't invariant under Morita equivalence. Can you see why? (I gave you a hint.)
Here's the cool part. There's a bicategory with rings as objects, bimodules as morphisms, and bimodule homomorphisms as 2-morphisms. There's a nontrivial theorem saying that equivalence in this bicategory is Morita equivalence!
It takes a while to understand what this means, and prove it.
The point is that given rings \(R\) and \(S\), an \((R,S)\)-bimodule can be thought of as a funny sort of 'morphism' from \(R\) to \(S\). We can tensor an \((R,S)\)-bimodule and an \((S,T)\)-bimodule over \(S\) and get an \((R,T)\)-bimodule. This is how we compose these funny morphisms.
So, I'm claiming two rings \(R\) and \(S\) are Morita equivalent iff there's an \((R,S)\)-bimodule \(M\) and an \((S,R)\)-bimodule \(N\) such that \(M \otimes_S N \cong R\) as an \((R,R)\)-bimodule, and \(N \otimes_R M\) as an \((S,S)\)-bimodule.
I'm teaching an online 'class' about this on the Category Theory
Community Server.
May 15, 2020
Good news: the price of solar power is dropping very quickly. This chart by Ramez Naam shows how it's going.
We are now 50-100 years ahead of the International Energy Agency's predictions in 2010. It turns out they were completely clueless.
Naam uses Wright’s Law to analyze the data. This rule of thumb says that each doubling of the total production of some technology leads to a fixed percentage decline in its price. Solar prices seem to be dropping 30-40% per doubling!
The world will change dramatically as the price of solar continues to plunge. We need this!
Read Ramez Naam's blog for more:
You can already see that in 2 dimensions rotations don't happen 'around an axis' - not an axis in the plane, anyway!
The right way to think about rotations in 3d is that they're 'in a plane'. That is, there's a plane where points on this plane go round and round... and the point that stands still is the center of rotation.
The 'axis' is just a line at right angles to this plane.
Rotations in 2d are also 'in a plane' — but now this plane is the whole of 2d space.
What about 4d? Now rotations take place in two planes. There are two 2d planes at right angles, where points go round and round staying in these planes, maybe at different speeds!
What about 5d? Again rotations take place in two planes. There are two 2d planes at right angles where points go round and round... but now there's also a line at right angles to both these planes, where points stay fixed! We're breaking up the dimensions this way: $$ 5 = 2 + 2 + 1 $$ I hope you get the pattern. In \(2n\) dimensions, there are \(n\) 2-dimensional planes at right angles where points go round and round, staying in these planes... possibly at different rates. In \(2n+1\) dimensions that's still true, but there is also a fixed axis.
For this reason, rotations in even-dimensional spaces are very different from rotations in odd-dimensional spaces! This shows up all over math and physics. For example, the 'Dynkin diagrams' for rotation groups look very different depending on whether the dimension is even or odd.
The situation gets even subtler when we think about 'spinors' — the gadgets sort of like vectors that describe spin-1/2 particles like the electron.
The math of spinors depends a lot on the dimension of spacetime, not just mod 2, but mod 8.
Now we've gone from something that's obvious if you think about it hard to something that's far from obvious. Why should spinning particles care about the dimension of space modulo 8? This is something I've studied over and over again, learning a bit more each time.
I wrote a quick intro to how spinors work in different dimensions here, back when I was first learning how supersymmetry is connected to the octonions:
That could be a good place to get started. Maybe too hard... maybe too sketchy... but short.
Someday I'm gonna write a book about this stuff. Only a book can go slowly from the most obvious facts to the most non-obvious, gradually making more and more things seem 'obvious'.
There's a lot to say about rotations in different dimensions!
May 17, 2020

Dirac took negative-energy electrons seriously. He realized a missing negative-energy electron would act like a positively charged particle with a positive amount of energy: a 'positron'. Then people actually found positrons. (They'd already seen them but couldn't believe it.)
Could he be right about taking negative probabilities seriously?
Negative numbers were invented by Venetian bankers. They started writing numbers in red to symbolize debts — hence the phrase "being in the red". Bankers couldn’t get so rich as they do if negative money didn’t exist.
But can you owe someone a probability?

In 1987 Feynman wrote an essay explaining how negative probabilities could be used. Read it! He explains things well:
The idea is that negative probabilities are only allowed in intermediate steps of a calculation, not the final results.
A nice example is the heat equation. It describes how the probability of finding a particle somewhere in a box spreads out in Brownian motion. We can solve it using Fourier series. The individual terms in the Fourier series can give negative probabilities!
Another example is the 'half-coin'. Say you make a bet where you get $1 if a coin comes up heads and $0 if it comes up tails. Say you want this bet to be the same as making two bets involving two separate 'half-coins'. You can do it with negative probabilities! Details here:
We use negative probabilities in quant finance since probability is just a KERNEL inside an integral, rarely a "real thing" outside of binary payoffs. So long as no arbitrage is satisfied. Only thing that matters is (by scaling) ∫densities=1. Similar to negative prices in oil.I guess it's not surprising that that financiers are already using negative probabilities, given that bankers first invented negative numbers!To visualize the intricacy, see my comments #RWRI on negative prices via arbitrage/squeezes.

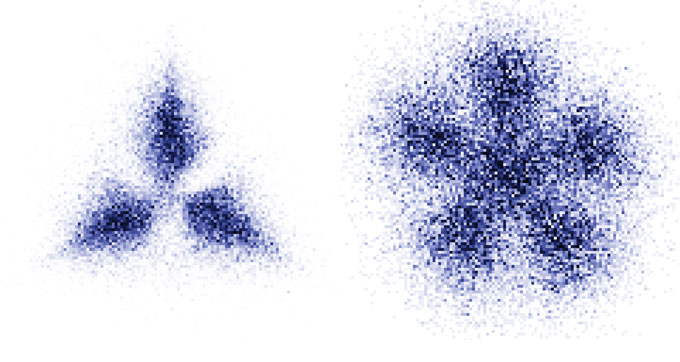
For noninteracting fermions in the plane, trapped in a harmonic oscillator potential, you get nice Pauli crystals with 1, 3, 6, 10, 15, ... atoms. These act like 'closed shells' in chemistry. These numbers show up because they're the triangular numbers 1, 1+2, 1+2+3, 1+2+3+4, etc.
Seeing a Pauli crystal is hard! You need to image all the atoms at once, and they keep wiggling around due to quantum fluctuations, so you have to take repeated images to get a good picture... and you have to keep rotating these images to get them to line up.
A team of physicists trapped lithium-6 atoms in a laser beam to create Pauli crystals. These atoms have 3 protons, 3 neutrons and 3 electrons; since the total 9 is odd they are fermions.
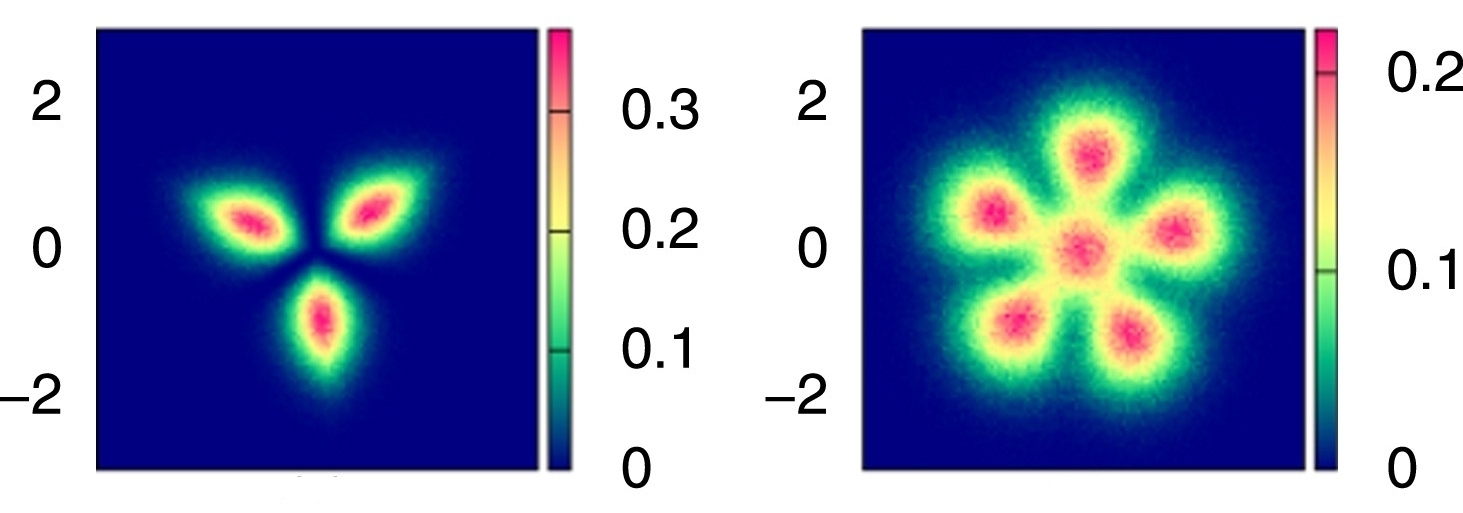
The experiment looks really cool!

Here's the paper on Pauli crystals:
'Dualities' are important because they show you two different-looking things are secretly two views of the same thing — or at least closely linked.
I'll sketch the idea of Isbell duality; you can see if you're ready for it.
![]()
Let \(\mathsf{C}\) be a category. Let \(\mathsf{C}^{\mathrm{op}}\) be its opposite category. Let \(\mathsf{Set}\) be the category of sets.
Let \([\mathsf{C}^{\mathrm{op}},\mathsf{Set}]\) be the category of all functors from \(\mathsf{C}^{\mathrm{op}}\) to \(\mathsf{Set}\). Such functors are called presheaves on \(\mathsf{C}\), and the Yoneda embedding is a functor $$ y \colon \mathsf{C} \to [\mathsf{C}^{\mathrm{op}},\mathsf{Set}] .$$
Let \([\mathsf{C},\mathsf{Set}]^{\mathrm{op}}\) be the opposite of the category of all functors from \(\mathsf{C}\) to \(\mathsf{Set}\). These are less famous; they're called copresheaves. There's a co-Yoneda embedding $$ z \colon \mathsf{C} \to [\mathsf{C},\mathsf{Set}]^{\mathrm{op}}. $$
The category of presheaves \([\mathsf{C}^{\mathrm{op}},\mathsf{Set}]\) is the free category with all colimits on \(\mathsf{C}\). It also has all limits, but its universal property is that any functor \(\mathsf{C} \to \mathsf{D}\) where \(\mathsf{D}\) has all colimits extends uniquely to a functor \([\mathsf{C}^{\mathrm{op}},\mathsf{Set}] \to \mathsf{D}\) that preserves colimits.
Dually, the category of copresheaves \([\mathsf{C},\mathsf{Set}]^{\mathrm{op}}\) is the free category with all limits on \(\mathsf{C}\). It also has all colimits, but its universal property is that any functor \(\mathsf{C} \to \mathsf{D}\) where \(\mathsf{D}\) has all limits extends uniquely to a functor \([\mathsf{C},\mathsf{Set}]^{\mathrm{op}} → \mathsf{D}\) that preserves limits.
Now the fun starts. Take the co-Yoneda embedding $$ z \colon \mathsf{C} \to [\mathsf{C},\mathsf{Set}]^{\mathrm{op}}. $$ Since \([\mathsf{C},\mathsf{Set}]^{\mathrm{op}}\) has all colimits, this functor extends uniquely to a functor $$ [\mathsf{C}^{\mathrm{op}},\mathsf{Set}] \to [\mathsf{C},\mathsf{Set}]^{\mathrm{op}}. $$ that preserves colimits.
Dually, take the Yoneda embedding $$ y \colon \mathsf{C} \to [\mathsf{C}^{\mathrm{op}},\mathsf{Set}]. $$ Since \([\mathsf{C}^{\mathrm{op}},\mathsf{Set}]\) has all limits, this functor extends uniquely to a functor $$ [\mathsf{C},\mathsf{Set}]^{\mathrm{op}} \to [\mathsf{C}^{\mathrm{op}},\mathsf{Set}] $$ that preserves limits.
So now we have functors sending presheaves to copresheaves: $$ [\mathsf{C}^{\mathrm{op}},\mathsf{Set}] \to [\mathsf{C},\mathsf{Set}]^{\mathrm{op}} $$ and copresheaves to presheaves: $$ [\mathsf{C},\mathsf{Set}]^{\mathrm{op}} \to [\mathsf{C}^{\mathrm{op}},\mathsf{Set}] $$ Isbell duality says these are adjoint functors!
Isbell duality seems to be the "mother of all dualities"... but I haven't stated it in its most general form.
Yesterday in the ACT@UCR seminar that I'm running, Simon Willerton explained how the Legendre transform arises from Isbell duality! Great talk!
Simon Willerton also showed how Dedekind's construction of the real line using cuts — and many other things! — come from the general form of Isbell duality.
Here you can see his slides, his paper, and a blog article he wrote on this stuff:
Unfortunately Gödel had spent time studying the U.S. constitution and claimed to have found an "inner contradiction" that made it possible for someone to become a dictator in a completely legal way. Einstein had tried to persuade him to just shut up about it... but then everything went awry.

Throughout the whole thing Einstein was joking around as usual.

The story appears in a letter — fragments of which are shown above — written by Oskar Morgenstern, who also accompanied Gödel to his citizenship hearing. This letter was lost for a while, but now you can read it here:

Gödel learned general relativity and found a solution of Einstein's equations that has closed timelike loops: in this universe your future is your past. It's called the Gödel universe.