These are paramilitary troops surrounding the Lincoln Memorial in Washington D.C. during protests of George Floyd's murder. In explaining this strategy Defense Secretary Esper said to U.S. governors:
Lincoln had a different opinion:


Whoops! You fools can't do anything right!

Better.
The second one came from here:
Let's dig into the history! Did the group theorist Burnside really think group representations were useless?
In 1897 William Burnside wrote the first book in English on finite groups. In the preface, he explained that "in the present state of our knowledge" there weren't theorems about groups that could best be proved by representing them as linear transformations (matrices). He wrote:
Cayley's dictum that "a group is defined by means of the laws of combination of its symbols" would imply that, in dealing with the theory of groups, no more concrete mode of representation should be used than is absolutely necessary. It may then be asked why, in a book that professes to leave all applications to one side, a considerable space is devoted to substitution groups [permutation groups], but other particular modes of representation, such as groups of linear transformations, are not even referred to. My answer to this question is that while, in the present state of our knowledge, many results in the pure theory are arrived at most readily by dealing with properties of substitution groups, it would be difficult to find a result that could most directly be obtained by the consideration of groups of linear transformations.
So, Burnside didn't actually say group representations were useless! His book was a "pure" study of finite groups, which "professes to leave all applications to one side".
But months after this book was published, he discovered the work of Georg Frobenius. Frobenius was a master of group representations! Burnside started using them in his own work on finite groups, and by the time he wrote the second edition of his book in 1911, he'd changed his tune completely:
Very considerable advances in the theory of groups of finite order have been made since the appearance of the first edition of this book. In particular the theory of groups of linear substitutions has been the subject of numerous and important investigations by several writers; and the reason given in the original preface for omitting any account of it no longer holds good. In fact it is now more true to say that for further advances in the abstract theory one must look largely to the representation of a group as a group of linear transformations.Are there results about finite groups that we only know how to prove using their representations on vector spaces? Yes! For example, the 'odd order theorem'. A group is 'solvable' if — roughly — it's built from abelian pieces. The odd order theorem says that group with an odd number of elements is solvable!

But be careful:
In 1904 Burnside showed that every group of order \(p^a q^b\) is solvable if p and q are prime. To do it he used group representations. But then, in 1972, Helmut Bender found a proof that avoids linear algebra!
It's an interesting challenge to state precisely how group
representations help us understand finite groups. For more on this,
read my imaginary dialog between Burnside and Frobenius in 'week252'. Skip past the stuff about astronomy
(if you can).
June 12, 2020
Ralf Wüsthofen
claims he has a simple one-page proof of Goldbach's conjecture which
"immediately leads to a proof of the inconsistency of arithmetic."

A classical bit is 0 or 1, but if we allow probabilities we can get anything in between. A qubit takes values on the unit sphere, but if we allow probabilistic 'mixed states' we can get anything in a 3-dimensional ball.
Then there's 'real quantum mechanics', where we use real numbers instead of complex numbers. This gives a 2d disk of mixed states.
All these are examples of 'generalized probabilistic theories' — a broad class of theories that people study to better understand what makes quantum mechanics and classical probability theory so special.
These theories use the math of convex sets.

A generalized probabilistic theory describes a system with a convex set of 'states'. If \(x\) and \(y\) are states, so is \(px + (1-p)y\) where \(0\le p\le 1\) is any probability. This is the result of preparing the system in the state \(x\) with probability \(p\) and the state \(y\) with probability \(1-p\).
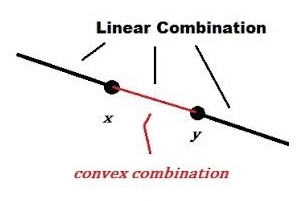
In ordinary complex quantum mechanics, the states of a qubit form a 3-dimensional ball. States on the surface are 'pure states': they're not convex combinations of other states. States in the interior are 'mixed'.
In the center is the state of maximum entropy.

The pure states of a qubit form a sphere. Physicists call it the 'Bloch sphere ', but mathematicians call it the 'Riemann sphere' or \(\mathbb{C}\mathrm{P}^1\). There are many ways to think about this, and I love them all. One way: take the complex numbers together with a 'point at infinity'.
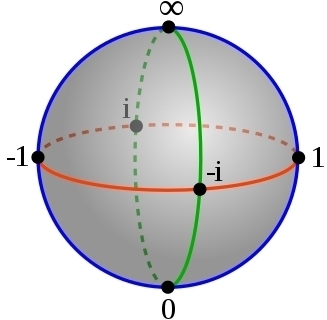
What if we use real numbers instead? In 'real quantum mechanics', the pure states of a 'real qubit' form a circle, also called \(\mathbb{R}\mathrm{P}^1\). It's the circle containing the real numbers in the above picture, like \(0,1,-1\), along with the point at infinity.
The mixed states of the real qubit form the 2d disk bounded by this circle.
Any 'formally real Jordan algebra' gives a generalized probabilistic theory. For example: the Jordan algebra of \(2\times 2\) self-adjoint complex matrices gives the theory of a qubit.
But you could use self-adjoint \(2 \times 2\) real matrices instead, and get the real qubit!
For more, try my gentle introduction to formally real Jordan algebras and their connection to projective geometry and quantum mechanics:
Now I'm writing a paper on Jordan algebras and Noether's theorem, thinking about these things a bit more deeply and learning a lot.
When you dissolve more and more sodium in ammonia, it changes from blue to bronze. And it starts conducting electricity just like a metal! Electrons and pairs of electrons called 'dielectrons' start moving freely through the solution.
I love condensed matter physics! I hadn't even known dielectrons were a thing: normally electrons repel. But in a sodium-ammonia solution, electrons pair up with opposite spins. Here's a new simulation of a dielectron, lasting 2.75 picoseconds:
The wavefunction of a loose electron in ammonia is smeared out over ~12 ammonia molecules, much bigger than one in water, which spreads out over ~5 water molecules.
This allows the formation of dielectrons, which are slightly bigger still.
As you add more sodium to ammonia, you get more of these loose electrons and dielectrons, and gradually a 'conduction band' arises — meaning that if they have the right momentum, these particles can move freely for long distances, like electrons in a metal!
I read about this in a new paper:

Can we understand evil using evolutionary biology, or perhaps game theory?
Psychologists have latched onto 3 personality traits, the 'dark triad', and tried to measure how much they are genetically inherited.

How are these traits defined?
But they have much in common. People with any of these traits tend to be callous, manipulative, dishonest and disagreeable.
They also tend to be less compassionate, agreeable, empathetic, satisfied with their lives — and less likely to believe they and other people are good.

Psychologists have tried to determine how much these traits are genetically inherited, by comparing identical vs. fraternal twins. (If a trait has a genetic component, it should be shared more often by identical twins than fraternal twins, even if these twins are raised the same way.)
Roughly speaking: psychopathy is 65% inherited, narcissism 60%, but Machiavellianism just 30%. (Technicaly, these are h2 figures.)
So, some have tried to develop evolutionary explanations of the dark triad traits, and why they persist despite their disadvantages. (Sub-clinical and clinical psychopaths form about 1% and 0.2% of the population, respectively; I know no estimates for the others.)
One theory is these traits are connected to a 'fast life strategy' with an emphasis on mating over parenting. People with these traits tend to have more sexual partners, but are less likely to form stable relationships. They tend to dress more attractively. They are also more likely to commit rape:
Dark triad traits are also advantageous in certain situations, called 'dark niches'. Narcissists are known to do well in job interviews and first dates. Machiavellianism works well in politics and finance. Psychopathy works well in street gangs.

Recently a fourth trait has been considered: 'everyday sadism'. For example, those bullies and internet trolls who enjoy making people suffer.
Separating out evil into distinct traits is a challenging job!
But to fight evil, we must understand it!
Here's an easy way to learn more:

This is the Bridge of Immortals, in Huangshan, in southern Anhui province. Like a hard theorem in mathematics that bridges two fields of mathematics, the view from the top is your reward for the difficult climb.


A Lie algebra is one of the more scary gadgets one meets as one first starts learning algebra, because the Jacobi identity looks unfamiliar. But it's secretly the product rule: $$ [x,[y,z]] = [[x,y],z] + [y,[x,z]] $$ is like $$ D(fg) = D(f) g + f D(g) $$ The easiest way to get a Lie algebra is to take square matrices, with the usual matrix multiplication, and define $$ [x,y] = xy - yx $$ Then it's obvious that \([x,x] = 0\), and the Jacobi identity follows from this 'product rule' $$ [x,yz] = [x,y] z + y [x,z] $$ which is easy to check.
The inventors of quantum mechanics noticed that you can treat functions as infinite-sized square matrices, and then the derivative \(Df\) of a function \(f\) can be written $$ Df = [\partial,f] = \partial f - f \partial $$ for some matrix \(\partial\), so the usual product rule follows from the product rule for matrices.
So, there's a Lie algebra where functions and the matrix \(\partial\) coexist, and these days it's called the 'Heisenberg algebra'. Basically it turns a bunch of calculus into the algebra of infinite square matrices!
There's an infinite amount to say about this, but I want to talk about something else. There are also gadgets with trilinear operations: operations that need 3 inputs, that are linear in each input. These are a bit scary at first, since the most familiar operations in math just take 2 inputs.
An example is a 'Lie triple system'.

Any Lie algebra gives a Lie triple system if we define \( [u,v,w] = [[u,v],w] \) The first rule in the definition of Lie triple system then follows from the antisymmetry of the Lie bracket, \([u,v] = -[u,v]\). The second rule is just the Jacobi identity in disguise. And the third, most complicated rule says each operation \([u,v,-]\) acts like 'differentiation', since it obeys a product rule similar to $$ D(wxy) = D(w)xy + wD(x)y + wxD(y) $$ Namely: $$ [u,v,[w,x,y]] = [[u,v,w],x,y] + [w,[u,v,x],y] + [w,x,[u,v,y]] $$ It's not so hard to remember if you keep this in mind.
But the really interesting Lie triple systems come from \(\mathbb{Z}/2\)-graded Lie algebras. These are Lie algebras split into an 'even part' \(\mathfrak{g}_0\) and an "odd part" \(\mathfrak{g}_1\) with $$ [\mathfrak{g}_0, \mathfrak{g}_0] \subseteq \mathfrak{g}_0 $$ $$ [\mathfrak{g}_0, \mathfrak{g}_1] \subseteq \mathfrak{g}_1 $$ $$ [\mathfrak{g}_1, \mathfrak{g}_0] \subseteq \mathfrak{g}_1 $$ $$ [\mathfrak{g}_1, \mathfrak{g}_1] \subseteq \mathfrak{g}_0 $$ Think "even plus even is even", etc.
In case you know about Lie superalgebras: \(\mathbb{Z}/2\)-graded Lie algebras are not those! They're just plain old Lie algebras chopped into an even and odd part obeying the rules above.
These rules imply the bracket of three odd things is odd: $$ [[\mathfrak{g}_1, \mathfrak{g}_1], \mathfrak{g}_1] \subseteq \mathfrak{g}_1 $$ So, if we take a \(\mathbb{Z}/2\)-graded Lie algebra and only keep the odd part \(\mathfrak{g}_0\), it becomes a Lie triple system if we define $$ [x,y,z] = [[x,y],z] $$ All this becomes a lot more exciting when you see how \(\mathbb{Z}/2\)-graded Lie algebras show up in geometry.
If you take a Lie group, its tangent space at the identity is a Lie algebra. But more generally, the tangent space at any point of a 'symmetric space' is a Lie triple system.
For example, the tangent space at any point of a sphere is a Lie triple system!
There's a Lie group \(\mathrm{SO}(n)\) of rotations in \(n\) dimensions. Its tangent space at the identity is a Lie algebra called \(\mathfrak{so}(n)\).
\(\mathrm{SO}(n)/\mathrm{SO}(n-1)\) is an \(n\)-sphere, which is a symmetric space.
\(\mathfrak{so}(n)/\mathfrak{so}(n-1)\) is the tangent space of the \(n\)-sphere at the north pole, which is a Lie triple system!
In other words, we can make \(\mathfrak{so}(n)\) into a \(\mathbb{Z}/2\)-graded Lie algebra by splitting it into two parts:
In 2018, three white dwarf stars were seen zipping across the Milky Way at over 1000 kilometers per second — thousands of times faster than a speeding bullet, fast enough to escape the galaxy. It was one of several clues that we were wrong about what causes many supernovae.
Type II supernovae happen when a big star collapses. But type Ia supernovae happen when a white dwarf explodes for some reason. We thought most of did this when they stole gas from a red giant companion. But no!
It now seems most type Ia supernovae happen when two white dwarfs spiral into each other and nearly collide. This is called — get ready for it! — a "dynamically driven double-degenerate double detonation".
Astronomers estimate about half a billion white dwarf binaries have merged in the Milky Way since its formation! If one-sixth of these mergers led to a type Ia supernova, there would be one supernova every 200 years — which is what we see.
And if type Ia supernovae work differently than we thought, that affects our understanding of the expansion of the Universe, since they're used as a 'standard candle' to measure the distance of faraway galaxies. Maybe we've got some things a bit wrong.
For more, read this:
Luckily we have ways of settling these disputes.

Or if that's not enough for you, try the nothing burger and nothing burger burger burger.
No matter how hungry you are, ZFC has a burger for you.
June 28, 2020

Jordan algebras are fascinating to me — but annoying. The usual definition uses the 'Jordan identity', which looks completely random. With help from David Madore, I found an equivalent definition that says more about what's good about Jordan algebras.
While they're weird, Jordan algebras come from physics. Jordan invented his algebras to study quantum mechanics.
In quantum mechanics, self-adjoint \(n\times n\) complex matrices are 'observables'. The product of observables is not an observable but $$ x \circ y = (xy + yx)/2 $$ is, and this gives a Jordan algebra.
There's also a Jordan algebra of self-adjoint \(n \times n\) real matrices, which works the same way. And there's also a Jordan algebra of self-adjoint \(n \times n\) quaternionic matrices! So, we can compare real and quaternionic quantum mechanics to ordinary complex quantum mechanics using Jordan algebras.
Working with Wigner and von Neumann, Jordan discovered a weirder fact. Self-adjoint \(n \times n\) octonionic matrices form a Jordan algebra... but only for \(n \le 3\).
The Jordan algebra of self-adjoint \(2 \times 2\) octonionic matrices is 10-dimensional and connected to superstring theory.
The Jordan algebra of self-adjoint \(3 \times 3\) octonionic matrices is 27-dimensional. It's called the 'Albert algebra' or 'exceptional Jordan algebra'. Its connection to physics, if any, remains quite obscure. I've been puzzling over this for years.
But in math, the exceptional Jordan algebra is great! Let me tell you just one reason why.
There's a systematic way to get three Lie algebras from a Jordan algebra: a little one, a medium-sized one and a big one. See the intro here for details:
Where is this going? Nobody knows yet. Jordan started by trying to understand and generalize quantum mechanics. But his algebras are also connected to the geometry of spacetime, and generalizations of that!
These mathematical ideas springing from physics could be clues leading us to better theories. Or, they could be leading us to dead ends. By now, I doubt I'll ever know.
The world offers us many mysteries; only a few will be solved during our lifetime.
To avoid frustration with cosmic questions I spend most of my time trying to solve little puzzles, like:
How exactly do Jordan algebras generalize quantum mechanics? What
makes complex quantum mechanics 'better' than the real or quaternionic
versions? Etc.
June 29, 2020
I've got a new paper on the arXiv. Here's my blog article about it,
with a link to the paper:
Meanwhile COVID-19 continues to spiral out of control in many US states: