

The Koide formula is a mysterious relation between the masses of the 3 charged leptons:
For the most part, serious physicists have given up seeking relations between masses of elementary particles, because it's so hard to explain any such relations.
Take squares whose areas are proportional to the masses of the electron, muon, and tau. Stack them up as shown. Then the Koide formula claims these squares fill up 2/3 of the larger square they all fit inside. So the rest, the gray area, is 1/3 of the larger square.
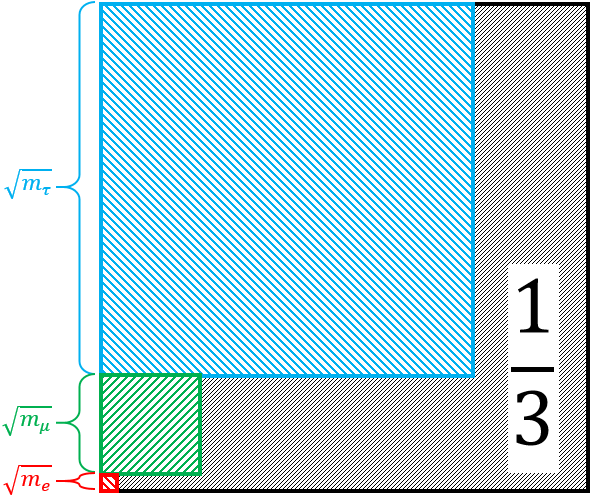
Math tells us that no matter what these three smaller squares are, they must fill up between 1/3 and all of the larger square. The Koide formula says the actual fraction is exactly halfway between 1/3 and 1.
Most physicists think the Koide formula must be a coincidence. Why? Due to interactions between particles, masses are not a simple thing. When you measure masses by colliding particles, what you get depends on how hard you smack the particles into each other!
This is called 'renormalization'.
Most physicists believe that fundamentally what matters is particle masses in extremely high-momentum collisions. But the masses in particle data books are for lower momentum!
Most physicists think it would take unmotivated 'fine-tuning' of particle masses at high momentum to get relations like the Koide formula to hold at low momentum.
Similarly, they say it requires fine-tuning to get the cosmological constant to be so small, or the Higgs mass to be as small as it is. These quantities are measured at low momentum — at least compared to the momentum scale of truly fundamental physics, where physicists think the laws are simple!
But some are beginning to question this.
There are two separate ideas at work here. One is 'naturalness':
But the other is the belief that simple laws are only found at very short distance scales, and thus high momenta. This says that the truly fundamental constants are not the ones we can measure at low momentum.
These two ideas interact with each other.
Due to renormalization, small changes in values of fundamental constants at large momentum can produce large changes in their values at low momentum. So, to get relations between these constants to hold even approximately at low momentum, we need to 'fine-tune' their values at high momentum.
Is this bad?
It's bad if you think 1) fine-tuning is bad and 2) the values of constants at high momentum are the only thing you get to 'tune'. (As if God could only turn those dials.)
Should we question assumptions 1) and 2)?
Sure, we should question all items of the conventional wisdom that
aren't backed by hard evidence! Particle physics is in a deeply
stuck state. But to make progress, it's not enough to question the
conventional wisdom. Ultimately, we need to propose concrete
alternatives that are compatible with everything we really actually
know. That's where it gets hard.
December 14, 2022
I love Max Richter's 8-hour minimal piece Sleep, even though I've only heard portions. The mp3 version sold by Amazon has nasty glitches in it — don't buy it. But this live version of portions of the piece is awesome — especially the first part, called Path 17 (before the ending of daylight). It features amazing vocals by Grace Davidson, enhanced by a subtle electronic treatment. It's falling down an infinite well into sleep.
Apparently this is from a live performance at the Sydney Opera House on September 11, 2016, where the audience was encouraged to sleep during the show.
Sleep has many separate parts, which are grouped into themes. I most like the "Path" theme, which has a creepy dreamy sound, due in large part to Grace Davidson's vocals. In the following part, this dreamy effect is enhanced by how she half-sings, half-hums along with her clear soprano singing:
I tried lots of things, and nothing worked. The manual was not helpful.
By now sun was setting. The temperature was in free fall. I started shivering. I called our landlord, who was off in sunny California.
He said "Oh, this happens every year."
When it gets cold enough, a pipe that carries exhaust from the gas furnace outside — carbon dioxide and water vapor — freezes up. The exhaust can't escape and the boiler, sensing this, shuts down.
He suggested two solutions. One was to run a hair dryer out the window and heat the pipe. The other was to boil kettles of water and carry them out there, for the same purpose.
But I had to find the right pipe.
I went outside and took some pictures.

Our landlord confirmed it: this was the pipe: wrapped in gray insulation, with white tape at the end, and then a smaller pipe leading down between two bricks to a drain.
I pulled off the smaller pipe, which was full of ice, and took it indoors. My wife and I boiled a kettle of water to melt the ice in this pipe.
That was easy. The harder part was melting the ice in the larger pipe covered with gray insulation. It was about 4 meters long and it went behind a metal drainpipe, making it hard to move without breaking it. It was, however, easy to remove the gray insulation without destroying it.

So, I had to thaw ice lurking somewhere in a 4-meter pipe. The end of the pipe was plugged with ice, so that was the obvious place to start, but for all I knew the whole pipe was full of ice.
I decided that kettles of hot water poured over the pipe would work better than running a hair dryer through the window - especially since I couldn't even open the window. So I started to work. Pouring near-boiling water on the plastic pipe, slowly so as not to waste it, soon produced a nice effect: tubes of ice, like icicles, started falling out of the pipe's end!
Then my wife found a thin metal rod. I used it to explore the pipe and pull out more ice.
At this point we decided to try turning on the furnace.
It worked! We triumphantly went to bed.
The next morning I got up and used another kettle of hot water and the metal rod to pull out some ice that was forming in the pipe. The weather was going to be below freezing for 4 days. Clearly this was going to be my new routine. Not pleasant, but tolerable. I even felt a slight sense of triumph: we'd figured out what to do!
Or so we thought.
The next morning the furnace stopped working.
I went outside and found, using the metal rod, that ice extended deep into the pipe. I started pouring kettles of water on it, to no avail. We borrowed an extension cord from our neighbors, ran it through the bathroom window, and started trying to melt ice in the pipe using a hair dryer. It still didn't work.
It was time to call our landlord again. It was 4 am in California. He was probably sleeping, happy and warm in his bed.
But at this point we were seething with rage at this stupid way of setting up a furnace: doomed to fail whenever it got really cold. So, we called him and, suppressing our irritation, asked him to call his boiler repair man. He did, but — surprise! — it being a cold wave, everyone was wanting their boilers fixed, just like us. We'd have to wait until "after 2 pm" the next day.
So, we hunkered down and readied ourselves for a cold night.
Luckily the house was blessed with a portable electric heater, good enough to warm one room. So we heated up the bedroom, found a second duvet, and went to bed with far more clothing than usual. This worked quite well. We didn't need to leave the heater on all night, we stayed quite cozy nestled under two duvets.
(For Americans unfamiliar with the word "duvet", an example is shown below.)

The next morning I noticed the electric heater's plug was becoming dangerously hot. Since it would be sadly ironic to die in a fire after all this, I went out and bought a new electric heater.
At 3 pm, the boiler repair man showed up. He was reassuringly competent and soon figured out a temporary solution: open a spigot below the boiler to let the problematic condensation drip into a bucket.
The boiler started!
The repair man promised to return next week when the temperature rises above freezing, and effect a permanent solution. So now I am pouring buckets of water into the sink twice a day. But I am happy as long as this is a predictable routine. All I really need is a predictable routine. Only if the bucket overflows overnight, or the furnace mysteriously gives out again, or the repair man fails to show up, will this story need to continue.
(In fact everything worked out fine, and it's supposed to stay
above freezing until we leave Edinburgh.)
December 22, 2022
Is C flat really different from B?
Here Adam Neely argues his evil twin into accepting the answer is yes:
First he explains why it's good to use the note C♭ as part of the G♭ major scale. Then he shows it has a different function than B. Then he uses math to show it has a different pitch if you're not trapped in equal temperament. Then finally he lets us hear the difference! It makes a huge difference when it's part of a chord.
But the cool part is the old keyboards where they were different. Here's a picture from a book showing some sixteenth-century keyboards. The second one lets us play a C flat that sounds different from a B!

You can read about such keyboards here — they have great names like 'archicembalo', 'arciogano', 'clavemusicum omnitonum' and 'cimbalo cromatico':
By the way, I found it funny how Adam's evil twin gets exasperated
when the math comes in. "Okay, we're now at the part of music theory
where we're multiplying notes."
December 23, 2022
I love Adam Neely's explanations of music theory and what it's like to
be a jazz musician struggling to make a living in New York. But I
wasn't so sure I liked his actual music. I'd call it electro-jazz .
It's packed with technically sophisticated harmonies and song
structures, and rhythmic tricks like quintuplets. But despite my love
for such stuff, it didn't move me.
This song, Bird on the Wing, actually does:
The beginning really jumps out at me, with its mix of live playing and glitchy electronics, all in a rhythm that's too complicated for me to parse. It produces a kind of sensory overload, but still catchy. But rejecting the essentially static nature of so much modern electronic dance music, this song has a chorus, and builds to an electric-guitar-dominated climax. And these jazzsters know how to use chord changes! Refreshing.
You can see a bass transcription of the piece here. It switches back and forth from 9:8 to 5:4, with a bit of 4:4 thrown in so it doesn't get too boring.
December 25, 2022
When Musk took over Twitter and started doing crazy bad stuff, I
stopped explaining math there and started doing it on Mathstodon. The number
of interesting people there quickly grew. (I credit Musk for this
more than myself.) Lately I've been having a lot of fun there,
and putting in a lot of work to invigorate the conversations there.
Like most things, it's more fun when I put more work into it.
On December 14th I asked: if you divide a square into 4 similar rectangles, what proportions can these rectangles have? A bunch of people joined in to find the 11 options. On December 15th I summarized our work on Mastodon, and later I wrote a more detailed report on my blog, since it's hard to find things diffusely spread among many Mastodon posts:
On December 20th I asked: how many elements does the free idempotent rig on 3 generators have? A bunch of people sprang into action and soon three had independently confirmed (using computers) that the answer is 284. I summarized their work on my blog:
On December
23rd I tried something different: studying a new purported proof of
the Four Color Theorem, which was only 6 pages long. The first mistake
I discussed turned out to be just a typo. On December
24th I dug into the paper's treatment of the generating function
for rooted planar graphs, which was merely ineffficient, not wrong.
But various other people, especially Noam Zeilberger and Simon Pepin
Lehalleur, discovered serious mistakes, and looking into it I found
more. By the end
of that day, I was prepared to say the proof could not be
salvaged. I tweeted a link to our findings, since I still have many more
followers on Twitter than Mathstodon, and this is the sort of news that
should get out.
December 29, 2022
This is a color-enhanced photo of the plains near the south pole of Mars, in spring. Water ice and carbon dioxide ice — 'dry ice' — are both active in this landscape.
Water ice frozen in the soil splits the ground into polygons. In the spring, frozen carbon dioxide below the surface turns into gas and shoots out through vents here and there. The gas carries along fine particles that drop to the surface in dark fan-shaped deposits.
This picture was taken near the South Pole, at latitude -85.044° and longitude 259.017°, by the HiRISE satellite. Here it's available here in many formats, and you can read a bit more about it:
It isn't in natural color, as seen by normal human eyes, because the infrared, red, and blue-green channels are displayed in red, green, and blue colors.
For more, try this article:
Among other things I explain the strange picture below, showing vents on Martian dunes near the North Pole.

Listening to the Brandenburg Concertos, and reading a bit about them, I realized they're a great example of the importance of luck.
Bach dedicated them to Christian Ludwig, Margrave of Brandenburg-Schwedt, hoping to get a job. But Ludwig didn't have enough musicians to play them. Bach didn't get the job. The score was left unused in the Margrave's library until his death.
When the Margrave of Brandenburg-Schwedt died, the scores of the concertos were sold for 24 groschen — about about US $20.
The autograph manuscript of the concertos was only rediscovered in the archives of Brandenburg by Siegfried Wilhelm Dehn in 1849. The concertos were first published in the following year — 128 years after they were written!
The manuscript of the Brandenburg Concertos was nearly lost in World War II, when it was being transported for safekeeping to Prussia. The train carrying it came under aerial bombardment, and the librarian guarding them escaped from the train to a nearby forest with the scores hidden under his coat. But by that time there were lots of copies of the score, so the music — the important part — could not be lost.
In 1977 a recording of the concertos was sent into space, on Voyager.
Now they seem iconic, necessary, and irreplaceble. But how would the world be different if Bach's Brandenburg Concertos were lost... or had become popular much earlier?
They were not an unprecedented bolt out of blue. Compare the Concerti con molti strumenti, by Vivaldi:
They're similar in some ways. And it's probably no coincidence: Bach spent time transcribing the works of Vivaldi. So if the Brandenburg Concertos had been lost, maybe we'd spend more time listening to Vivaldi!