

I've been away from my piano since September. I really miss playing it. So, I've been sublimating my desire to improvise on this instrument by finally learning a bunch of basic harmony theory, which I practice just by singing or whistling.
For example, I'm getting into modes. The following 7 modes are all obtained by taking the major scale and starting it at different points. But I find that's not the good way for me to understand the individual flavor of each one.
Much better for me is to think of each mode as the major scale (= Ionian mode) with some notes raised or lowered a half-step — since I already have an intuitive sense of what that will do to the sound. For example, anything with the third lowered a half-step (♭3) will have a minor feel. And Aeolian, which also has the 6th and 7th lowered (♭6 and ♭7), is nothing but my old friend the natural minor scale!
A more interesting mode is Dorian, which has just the 3rd and 7th notes lowered a half-step (3♭ and 7♭). Since this 6th is not lowered this is not as sad as minor. You can play happy tunes in minor, but it's easier to play really lugubrious tear-jerkers, which I find annoying. The major 6th of Dorian changes the sound to something more emotionally subtle. Listen to a bunch of examples here:
Some argue that the Dorian mode gets a peculiarly 'neutral' quality by being palindromic: the pattern of whole and half steps when you go up this mode is the same as when you go down:
This may seem crazily mathematical, but Leibniz said "Music is the pleasure the human mind experiences from counting without being aware that it is counting."
Indeed, there is a marvelous theory of how modes sound 'bright' or 'dark' depending on how many notes are sharped — that is, raised a half-tone — or flatted — that is, lowered a half-tone. I learned about it from Rob van Hal, here:
The more notes are flatted compared to the major scale, the 'darker' a mode sounds! The fewer are flatted, the 'brighter' it sounds. And one, Lydian, is even brighter than major (= Ionian), because it has no flats and one sharp!
So, let's list them from bright to dark. Here's a chart from Rob van Hal's video:
You can see lots of nice patterns here, like how the flats come in 'from top down' as the modes get darker: that is, starting at the 7th, then the 6th and then the 5th... but also, interspersed with these, the 3rd and then the 2nd.
But here's something even cooler, which I also learned from Rob van Hal, though he was surely not the first to discover it.
If we invert each mode — literally turn it upside down, by playing the pattern of whole and half steps from the top of the scale down instead of from bottom to top — the brighter modes become the darker modes, and vice versa!
Let's see it! Inverting the brightest, Lydian:
we get the darkest, Locrian:
Inverting the 2nd brightest, the happy Ionian (our familiar friend the major scale):
we get the 2nd darkest, Phrygian:
Inverting the third brightest, Mixolydian:
we get the third darkest, the sad Aeolian (our friend the natural minor):
And right in the middle is the palindromic Dorian:
What a beautiful pattern!
By the way, it's also cool how both the ultra-bright Lydian and the ultra-dark Locrian, and only these modes, have a note that's exactly half an octave above the 1. This is a very dissonant thing for a mode to have! In music jargon we say it like this: these modes have a note that's a tritone above the tonic.
In Lydian this note is the sharped 4th, which is a 'brighter than usual 4th'. In Locrian it's the flatted 5th, which is a 'darker than usual 5th'. But these are secretly the same note, or more technically 'enharmonic equivalents'. They differ just in the role they play — but that makes a big difference.
Why do both Lydian and Locrian contain the tritone above the tonic? It's not a coincidence: the tritone is mapped to itself by inversion of the octave, and inversion interchanges Lydian and Locrian!
This stuff is great, especially when I combine it with actually singing in different modes and listening to how they sound. Why am I learning it all just now, after decades of loving music? Because normally when I want to think about music I don't study theory — I go to the piano and start playing!
For music, more important than the mathematical patterns relating different modes is learning the 'personality' of individual modes and how to compose or improvise well in each mode.
Here are some introductions to that! Since I'm in awe of Rob van Hal I will favor his when possible. But there are many introductions to each mode on YouTube, and it's worth watching a lot, for different points of view.
Locrian is so unloved that I can't find a good video on how to compose in Locrian. Instead, there's a good one on how Björk created a top 20 hit that uses Locrian:
There's also a good one about Adam Neely and friends trying to compose in Locrian:
Jake Lizzio also creates a far-out tune in Locrian here:
November 8, 2022
When you first learn about the major scale it's fairly
straightforward, because they tell you about just one major
scale. But the minor scale is more tricky, because they tell you
about three — or actually four, two of which are
the same!
The most fundamental of these is the natural minor scale. The C major scale goes
The C natural minor scale goes
As you can see the 3rd, 6th and 7th notes of the scale are 'flatted': moved down a half-tone compared to the major scale. This gives the natural minor scale a darker, even 'sadder' quality compared to the major scale.
I prefer to work with note numbers instead of note names, not because I'm a mathematician so I love numbers, but because then we can simultaneously talk about different keys at once, not just the key of C. In this approach we call the notes of the major scale
and then the natural minor scale is
Don't ask me why the flats are written in front of the numbers now instead of after them — it's just a convention.
Now, one thing about 'common practice' western harmony is the 7th tone plays a special role. It's just a half-step below the 8, and we act like that dissonance makes it want very strongly to go up to the 8. The 8 is one octave above the 1, twice the frequency. Either the 1 or 8 instantly serves as a home base: we feel like a piece or passage is done, or momentarily at peace, when we play these notes. We say the 7 wants to 'resolve' to the 8, and we call it the 'leading-tone' for this reason: it suggests that we've almost reached the tonic, and makes us want to get there!
There's much more we could say here, but it all combines to make people want a scale that's like minor but contains the 7 instead of the ♭7. And since this scale is motivated by reasons of harmony theory, it's called the harmonic minor scale. It goes like this:
However, now people singing this scale find it mildly awkward to jump up from ♭6 to the 7 because the distance between them is larger. In fact it's 3 half-tones, larger than any step in the major or natural minor scale! One way to shrink this gap is to raise the ♭6 to a 6 as well. This gives the melodic minor scale:
By now we're almost back to the major scale! The only difference is the flatted 3. However, that's still a lot: the ♭3 is considered the true hallmark of minorness. There are reasons for this, like the massive importance of the 1 3 5 chord, which serves to pound home the message "we're back to 1, and this is the major scale, so we are very happy". Playing 1 ♭3 5 says "we're back to 1, but this is minor, so we are done but we are sad".
However, singing up the scale is different from singing down the scale. When we sing up the melodic major scale we are very happy to sing the 7 right before the 8, because it's the leading-tone: it tells us we're almost home. But when we sing down we don't so much mind plunging from the 8 down to ♭7, and then it's not so far down to ♭6: these are both steps of a whole tone. If we do this we are singing in the natural minor scale. So what I called 'melodic minor' is also called 'melodic minor ascending', while natural minor is also called 'melodic minor descending'.
Here I should admit that while this is an oft-told pedagogical story, the actual reality is more complex. Good composers or improvisers use whatever form of minor they want at any given moment! However, most western musicians have heard some version of the story I just told, and that does affect what they do.
To listen to these various forms of the minor scale, and hear them explained more eloquently than I just did, try this:
Grazie Terzian is the patient teacher of music theory I wish I'd had much earlier. You may feel a bit impatient listening to her carefully working through various scales, but that's because she's giving you enough time for the information to really sink into your brain!
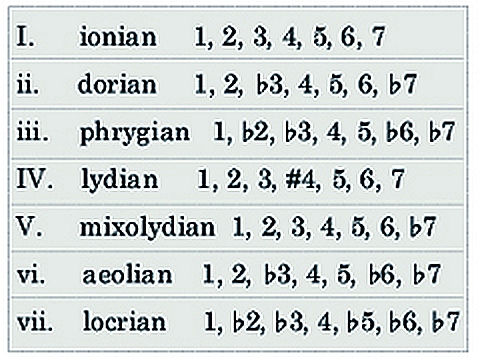
Anyway: we've seen one form of major scale and three forms of minor, one of which has two names. All these scales differ solely in whether or not we flat the 3, 6 or 7. So, we can act like mathematicians and fit them into a cube where the operations of flatting the 3, 6 or 7 are drawn as arrows:
Here to save space I've written flatted notes with little superscripts like \(3^\flat\) instead of ♭3: it makes no difference to the meaning.
This chart shows that flatting the 3 pushes our scale into minor territory, while flatting the 6 and then the 7th are ways to further intensify the darkness of the scale. But you'll also see that we're just using a few of the available options!
In part 1 I showed you another way to modify the major scale, namely by starting it at various different notes to get different 'modes'. If we list them in order of the starting note — 1, 2, 3, etc. — they look like this:

For example, Ionian is just major. But we saw that it is also very nice to list the modes from the 'brightest' to the 'darkest'. Rob van Hal made a nice chart showing how this works:
Skipping over Lydian, which is a bit of an exception, we start with major — that is, Ionian — and then start flatting more and more notes. When we reach the Phrygian and Locrian we flat the 2 and then the 5, which are very drastic things to do. So these modes have a downright sinister quality. But before we reach these, we pass through various modes that fit into my cube!
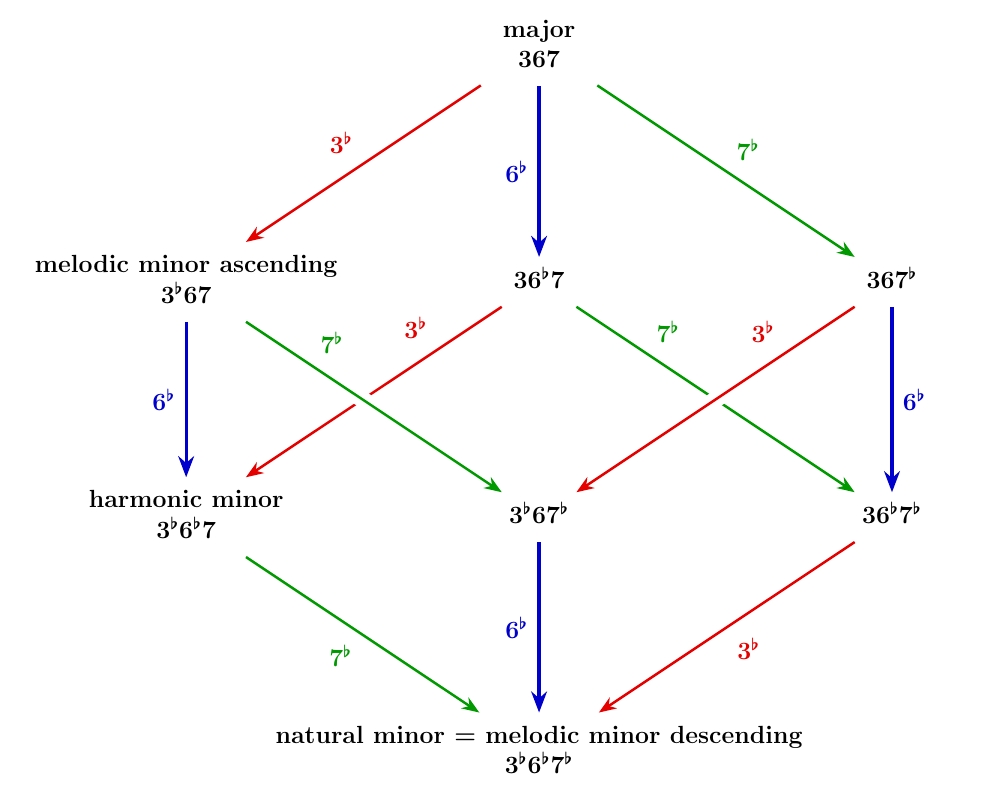
Let's look at them:
We're now tracing out a different path from top to bottom. Ionian has no notes flatted. In Mixolydian we flat the 7. In Dorian we also flat the 3. Then in Aeolian we also flat the 6.
I mentioned that the ♭3 is considered the true hallmark of minorness. Thus, in the classification of modes, those with a flatted 3 are considered 'minor' while those without are considered 'major'. So in our new path from the cube's top to its bottom, we switch from major to minor modes when we pass from Mixolydian to Dorian.
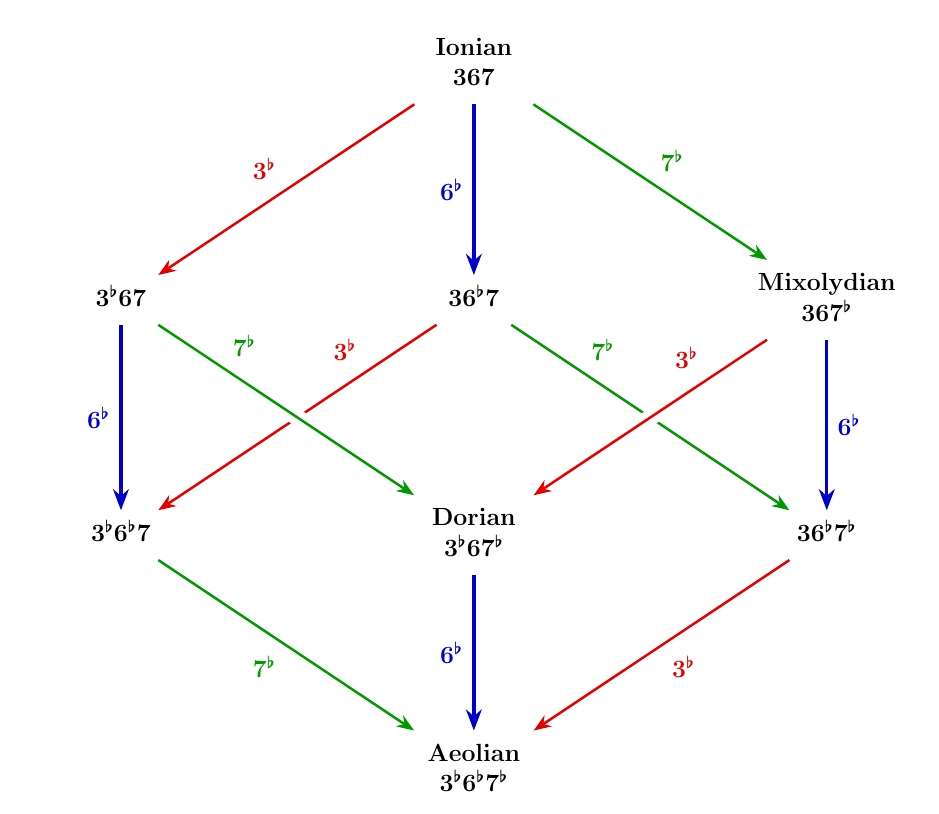
Note that Ionian is just our old friend the major scale, and Aeolian is our friend the natural minor. We can combine the two cubes I've showed you, and see how they fit together:
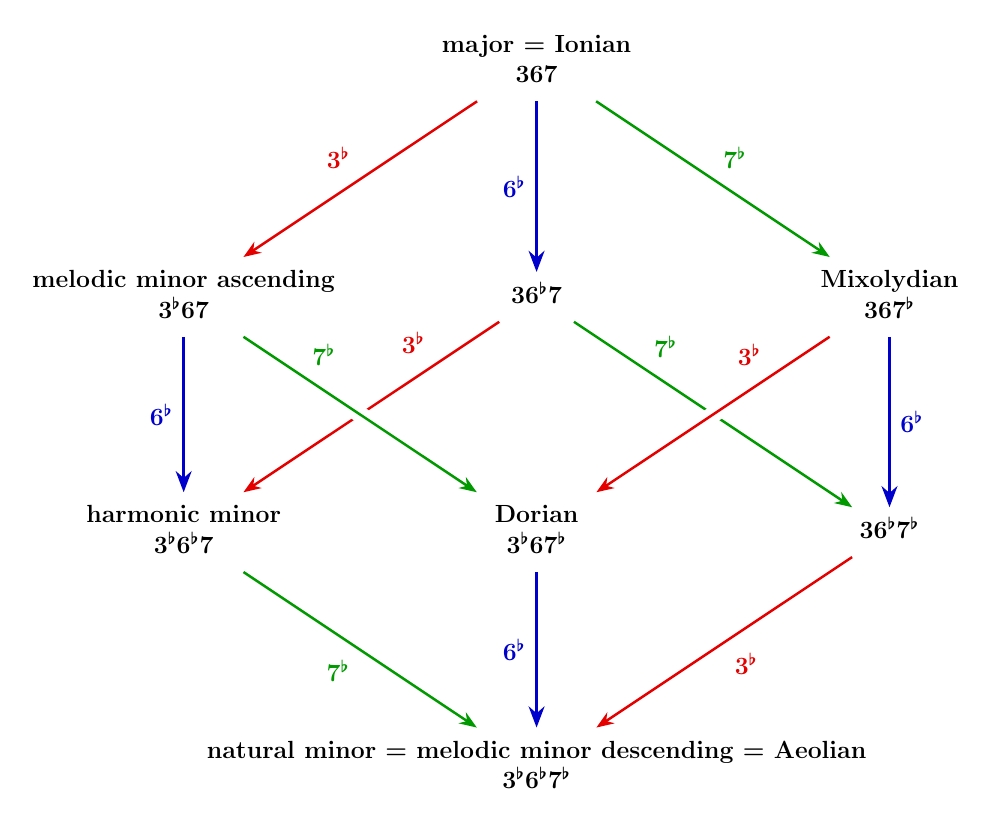
Now we can get from the top to Dorian following two paths that pass only through scales or modes we've seen! Similarly we can get from melodic minor ascending to the bottom following two paths through scales or modes we've seen. In general, moving around this cube through the course of a piece provides a lot of interesting ways to subtly change the mood.
But two corners of our cube don't have names yet! These are more exotic! But of course they exist, and are sometimes used in music. The mode
is called harmonic major, and it's used in the Beatles' 'Blackbird'. The mode
is called the melodic major scale, or also 'Mixolydian flat 6' or 'Aeolian dominant'. It's used in the theme song of the movie The Mask of Zorro, called 'I Want to Spend My Lifetime Loving You'.
So, let's add these two modes to our cube:

This is the whole enchilada: a 'commuting cube', meaning that regardless of which path we take from any point to any other point, we get the same mode in the end. We can also strip it of all the musical names and think of it in a purely mathematical way:
We could go further and study a 5-dimensional hypercube where we also
consider the results of flatting the 2 and 5. That would let us
include darker and scarier modes like Phrygian, Phrygian dominant and
Locrian — but it would be tougher to draw!
November 9, 2022

Cohomology is often used to count holes in topological spaces, and — for example — classify line bundles over these spaces, based on the idea that a line bundle can 'twist' as it goes around a hole, as in the Möbius strip above. But modern number theory says that algebraic numbers like can be seen as functions on tiny spaces... which still have holes! So cohomology shows up here too.
The trick is to think of a 'number ring' like $$ \mathbb{Z}[\sqrt{-5}] = \{a + b\sqrt{-5} : \, a,b \in \mathbb{Z} \} $$ as the ring of functions on a kind of space, called a 'scheme'. Then ideals in your number ring act like line bundles on this space!
You can multiply a section of a line bundle by a function; similarly you can multiply an element of an ideal by an element of your number ring. That's how the analogy starts.
Carrying it much further, people developed 'class field theory', which applies cohomology to number theory. I've found Jürgen Neukirch's book Algebraic Number Theory to be one of the most fun ways to learn about this stuff. His love for the subject shines through.
Let me explain one tiny idea: how the ideal class group of a number ring is a cohomology group.
An ideal \(I\) of a number ring \(K\) gives a module of \(K\), just as a line bundle over a topological space gives a module for the ring of continuous functions on that space. In both cases we don't get just any old module, either: we get a locally free module of rank 1. This is an algebraic way of saying that 'locally', our module looks just like a copy of the ring it's a module of. But 'globally' it can twist around, like our pal the Möbius strip.
Now, some line bundles on a space are 'trivial'. These give modules of its ring of functions that don't twist around at all! These modules are not just 'locally free of rank 1' but actually free of rank 1. This is a fancy way to say they're isomorphic to the ring itself.
Similarly for ideals of a number ring \(K\). Some are actually free of rank 1: that is, isomorphic to \(K\) itself. These are the 'principal' ideals.
The analogy continuues: we can multiply line bundles, and also multiply ideals.
To multiply or 'tensor' two line bundles \(L\) and \(L'\) we take the tensor product of their fibers, which are 1d vector spaces, and get a new 1d vector space which we take as the fiber of a new line bundle \(L \otimes L'\).
To multiply two ideals \(I\) and \(I'\) of a number ring we simply multiply elements of \(I\) with elements of \(I'\) and take all possible sums, getting an ideal \(II'\).
When we multiply line bundles their twistiness gets added! This suggests that we should form an abelian group from line bundles, or some equivalence classes of line bundles. We can do it: just take isomorphism classes of line bundles and make it into a group using $$ [L] [L'] = [L \otimes L'] $$ We can do something similar with ideals of a number ring, but it's a bit subtler. We get a group called the 'ideal class group'.
The subtlety in the number theory case is that not every locally free module of rank 1 comes from an ideal: we need more general things called 'fractional ideals'. But if just talk about modules this subtlety disappears: we can just using locally free modules of rank 1.
So: in both topology and number theory, there's an important abelian group whose elements are the ways that a line bundle (or locally free module of rank 1) can be twisted!
And some good news: in both cases, this is a cohomology group!
If \(X\) is a topological space, its isomorphism classes of complex line bundles correspond to elements of the group \(H^1(X,\mathbb{C}^\ast)\). This is the first cohomology of \(X\) with coefficients in \(\mathbb{C}^\ast\), the group of invertible complex numbers!
If \(K\) is a number ring, its ideal class group is isomorphic to \(H^1(K,\mathbb{G}_m\). This is the first cohomology of \(K\) with coefficients in \(\mathbb{G}_m\).
What's \(\mathbb{G}_m\)? It stands for 'multiplicative group', and it's analogous to \(\mathbb{C}^\ast\). But here it actually stands for a sheaf of groups:
And morally, not literally, it's first cohomology because it describes how something like a line bundle twists as we march around a 1-dimensional loop in some space — a scheme — and it has coefficients in \(\mathbb{G}_m\) because the 'twist' is an invertible number of some sort.
This is so cool. It means you can use your topological intuition in
number theory!
November 14, 2022
I wrote my regular column for the Notices of the American
Mathematical Society in a rush this time, because someone else's
article fell through and there was extra space:
One key element of this longer version was realizing that the vertices of an icosidodecahedron can be partitioned into the vertices of a regular octahedron and three 'golden boxes': rectangles with the proportions \(1:\Phi:\Phi^2\), where \(\Phi\) is the golden ratio. I recruited some people to draw this. On Mathstodon, Greg Egan made this image:
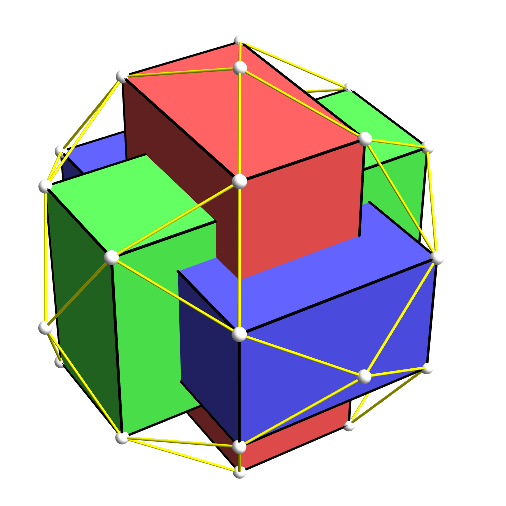
Rahul Narain made these:
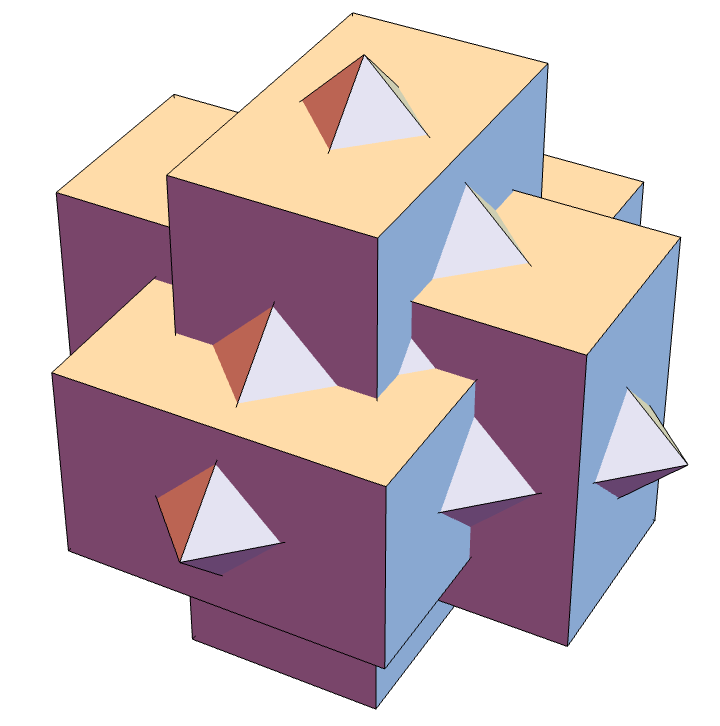
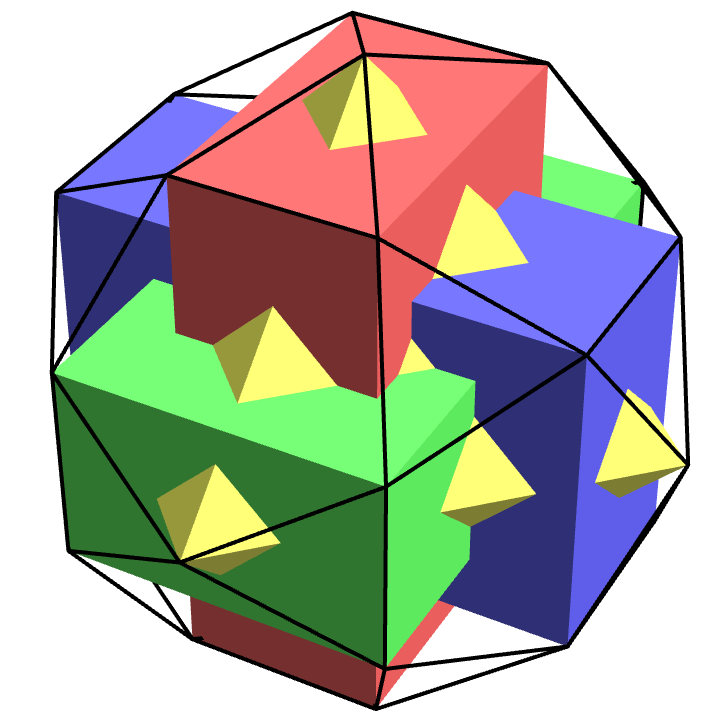

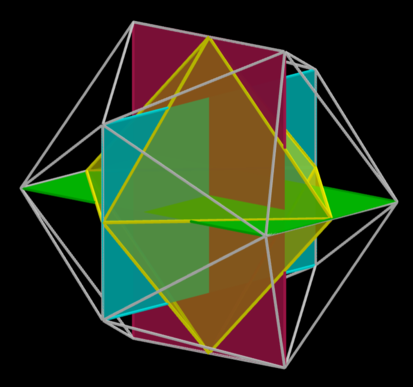

I'll put a more polished version of the longer article on the arXiv after the Notices version comes out. In my next columns I want to talk about roots of polynomials and, separately, the moduli space of acute triangles and the moduli space of elliptic curves.