

I enjoy the paintings of Édouard Cortès because while he's called a 'postimpressionist', he captures for me a certain essence of the impressionist ideal. His paintings, or at least the ones I like best, are rather limited in their range of subject matter. But he seems to have perfected a way of capturing the feel of wet or snowy Paris streets, which makes the warmth of indoor lights even more beckoning.
Above is one of his paintings of the Place Vendome. Below is his painting of Le Quai de la Tournelle and Notre Dame.


Go back to my September 26th
entry to see where we left off.
October 3, 2022
As a warmup for computing the entropy of a box of gas, let's figure
out the entropy of a single particle in a box!
We'll start by working out its partition function. And we'll only do a particle in a one-dimensional box. It's easy enough:

But the whole idea raises some questions....
Some people get freaked out by the concept of entropy for a single particle — I guess because it involves probability theory for a single particle, and they think probability only applies to large numbers of things.
I sometimes ask them "how large counts as "large"?"
In fact the foundations of probability theory are just as mysterious for large numbers of things as for just one thing. What do probabilities really mean? We could argue about this all day: Bayesian vs. frequentist interpretations of probability, etc. I won't.
Large numbers of things tend to make large deviations less likely. For example the chance of having all the gas atoms in a box all on the left side is less if you have 1000 atoms than if you have just 2. This makes us worry less about using averages and probability.
But the math of probability works the same for small numbers of particles.
Even better, knowing the entropy of one particle in a box will help us understand the entropy of a million particles in a box — at least if they don't interact, as we assume for an 'ideal gas'.
But why a one-dimensional box?
One particle in a 3-dimensional box is mathematically the same as 3 noninteracting distinguishable particles in a one-dimensional box! The \(x, y,\) and \(z\) coordinates of the 3d particle act like positions of three 1d particles!
So, we start with one particle in a 1-dimensional box. I showed you how to compute its partition function and get $$ Z(\beta) = \frac{L}{h} \sqrt{\frac{2\pi m }{\beta}} $$ From this we can compute its expected energy, free energy and entropy — and we'll do that next! You'll need to remember how to compute these things from the partition function:


Yesterday we worked out the partition function of a particle in a 1-dimensional box. From this we can work out its expected energy. Look how simple it is! It's just \(\frac{1}{2}kT\), where \(k\) is Boltzmann's constant and \(T\) is the temperature!
Why so simple?
We can use the chain rule $$ \frac{\partial}{\partial \beta} \ln Z = \frac{1}{Z} \frac{\partial Z}{\partial \beta} $$ to see only the power of \(β\) in $$ Z = \frac{L}{h} \sqrt{\frac{2\pi m }{\beta}} $$ matters, not the constants in front: they show up in \(\partial Z/d \beta\), but also in \(1/Z\), and they cancel. The length \(L\), the mass \(m\), Planck's constant \(h\), the factor of \(2\pi\)... none of this junk matters! Not for the expected energy, anyway! Because \(Z\) is proportional to \(\beta^{-1/2}\), we simply get \( \langle E \rangle = \frac{1}{2}k T\).
More generally, the partition function always decreases with increasing \(\beta\). Do you see why? And if the partition function of a system is proportional to \(\beta^{-c}\), its expected energy will be \(c\) times \(kT\).
But when is the partition function of a system proportional to \(\beta^{-c}\,\)? It's enough for the system's energy to depend quadratically on \(n\) real variables — called 'degrees of freedom'. Then \(c = n/2\).
We've already seen an example with 2 degrees of freedom: the classical harmonic oscillator. On September 25th we saw that in this example \(Z \propto 1/\beta\). This gives \(\langle E \rangle = kT\).
In fact, what we're seeing now is just another view of the equipartition theorem! I proved it a different way on August 18th. But the partition function for the system below is proportional to \(\beta^{-c}\) where \(c = n/2\), and that's another reason its expected energy is \(\frac{1}{2}nkT\).

Here's another thing to consider:
While our particle in a 1d box has \(2\) degrees of freedom — position and momentum — its energy depends on just one of these, and quadratically on that one. So its expected energy is \(\frac{1}{2}nkT\) where \(n = 1\), not \(n = 2\).
So here's a puzzle for you. Say we have a harmonic oscillator with spring constant \(\kappa\). As long as \(\kappa \gt 0\), the energy depends quadratically on \(2\) degrees of freedom so \(\langle E \rangle = kT\). But when \(\kappa = 0\) it depends on just one, and suddenly \( \langle E \rangle = \frac{1}{2} kT\). How is such a discontinuity possible?
In other words: how can a particle care so much about the difference between an arbitrarily small positive spring constant and a spring constant that's exactly zero, making its expected energy twice as much in the first case?
I'll warn you: this puzzle is deliberately devilish. In a way
it's a trick question!
October 5, 2022

October 6, 2022
The entropy of a classical ideal gas is given by a simple
formula... except for a mysterious constant that involves a bit of
quantum mechanics!
Today we'll see how entropy works for a single classical particle in a 1-dimensional box of length \(L\).

We've already worked out the expected energy \(\langle E \rangle\) and free energy \(F\) of our particle. This makes it easy to work out its entropy:

The answer looks a lot like the entropy of an ideal gas! That's no
coincidence — we're almost there now.
October 10, 2022

One of the most amazing discoveries of 20th-century physics: particles are waves. The wavelength of a particle is Planck's constant divided by its momentum!
This was first realized by Louis de Broglie in his 1924 PhD thesis, so it's called the de Broglie wavelength.
Why am I telling you this? Because I want to explain and simplify the formula for the entropy of a particle in a box. Even though I derived it classically, it contains Planck's constant! So, it will become more intuitive if we think a bit about quantum mechanics.
This week we'll see an intuitive explanation for our formula of the
entropy of a particle in a 1d box. We'll use this intuition to
simplify our formula. That will make it easier to generalize to \(N\)
particles in a 3d box — our ultimate goal.
October 11, 2022
Particles are waves! Their wavelength is shorter when their momentum
is bigger. And the warmer they are, the bigger their momentum tends to be.
So there should be a formula for the typical wavelength of a warm
particle. And here it is!
It helps us visualize the world.

We get this approximate formula from a blend of ideas. Classical mechanics says kinetic energy is \(E = p^2/2m\). Classical stat mech says \(\langle E\rangle = 3kT/2\). Quantum mechanics says \(\lambda = h/p\). So, we can optimistically put these formulas together and see what we get!

We derived \(\langle E\rangle = \frac{3}{2} kT\) classically on August 18th and 19th. But it's close to correct for a single quantum particle in a big enough box (or gas of low enough density) at high enough temperatures. Otherwise quantum effects kick in: quantized energy levels and Bose/Einstein statistics!
Worse, \(\langle E \rangle = \frac{3}{2} kT\) and \(E = p^2/2m\) do not imply \(p = \sqrt{3mkT}\), even if \(p\) here means the magnitude of the momentum vector. The arithmetic mean of a square is not the square of the arithmetic mean!
So, we say the 'root mean square' of \(p\) is \(\sqrt{3mkT}\).
Similarly, even if the root mean square of \(p\) is \(\sqrt{3mkT}\) and quantum mechanically \(\lambda = h/p\), we cannot conclude that the root mean square of \(\lambda\) is \(h/\sqrt{3mkT}\). Again, you cannot pass a root mean square through a reciprocal!
So, we're really getting that some kind of 'harmonic root mean square' of the de Broglie wavelength \(\lambda\) is \(h/\sqrt{3mkT}\). With more work we could compute the arithmetic mean of this wavelength — i.e., its expected value — using either classical or quantum stat mech. I was too lazy to do that, but Greg Egan computed the expected value of the de Broglie wavelength classically and got $$ \frac{h}{\sqrt{\frac{\pi}{2} m k T}} $$
So, we can think of $$ \frac{h}{\sqrt{3 m k T}} $$ as a rough approximation to this, if we like. It's \(0.723\) as big.
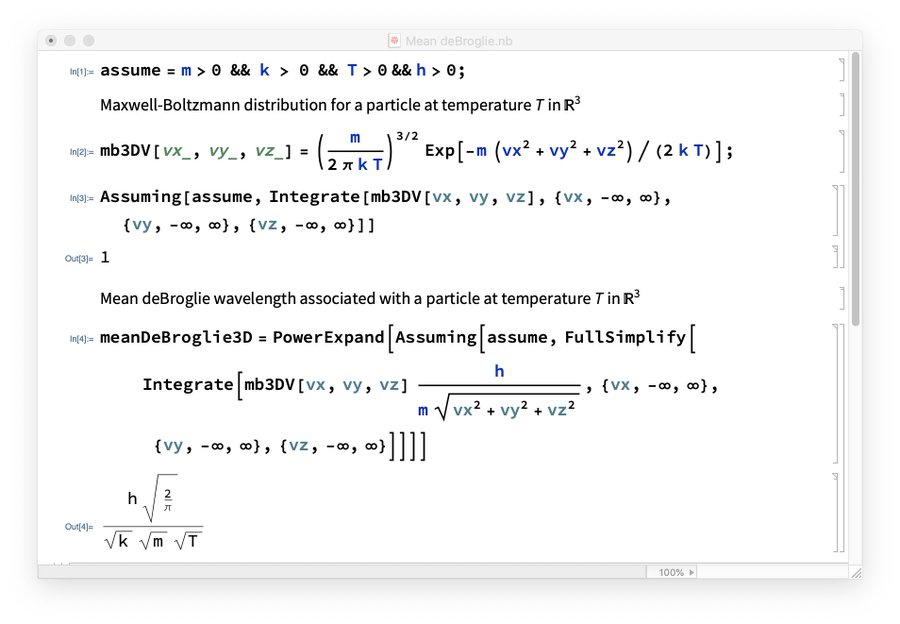

Particles are also waves! Even in classical mechanics you can understand the entropy of a particle in a 1d box as the log of the number of wavelengths that fit into that box...
...times Boltzmann's constant, plus a small correction.
We've already worked out the entropy of a classical free particle in a 1d box, so expressing it in terms of the so-called 'thermal wavelength' \(\Lambda\) is just a little calculation, shown below. Note: \(\Lambda\) is not what we got when we crudely estimated the average wavelength of a warm particle!

Still, \(\Lambda\) will be very useful for thinking about the partition function of a particle in a 1d box. And the volume \(\Lambda^3\) will show up when we compute the partition function and entropy of a particle in a 3d box... or our holy grail, the ideal gas.
We're almost there!
October 13, 2022

The partition function of a classical particle in a box is incredibly simple and beautiful! For a 1-dimensional box, it's just the length of the box divided by the thermal wavelength \(\Lambda\). For a 3-dimensional box, it's just the volume divided by \(\Lambda^3\).
The calculation works the same way in any dimension. Integrate over position and you get the (hyper)volume of your box. Integrate over momentum and you get \(1/\Lambda^n\), where \(n\) is the dimension of your box. And don't forget that the correct measure includes the right power of Planck's constant to make the integral dimensionless!

Once we know the partition function \(Z\), we can compute the entropy and other good things. It's also easy to include more particles... though the answer will depend on whether these particles are distinguishable or indistinguishable!
I'll do all this next.
October 14, 2022
Today we finally reach the climax. We'll figure out the entropy of an ideal gas!
It matters whether we can tell the difference between the particles or not. Only if they're indistinguishable will we get the experimentally observed answer.
Let's do it!
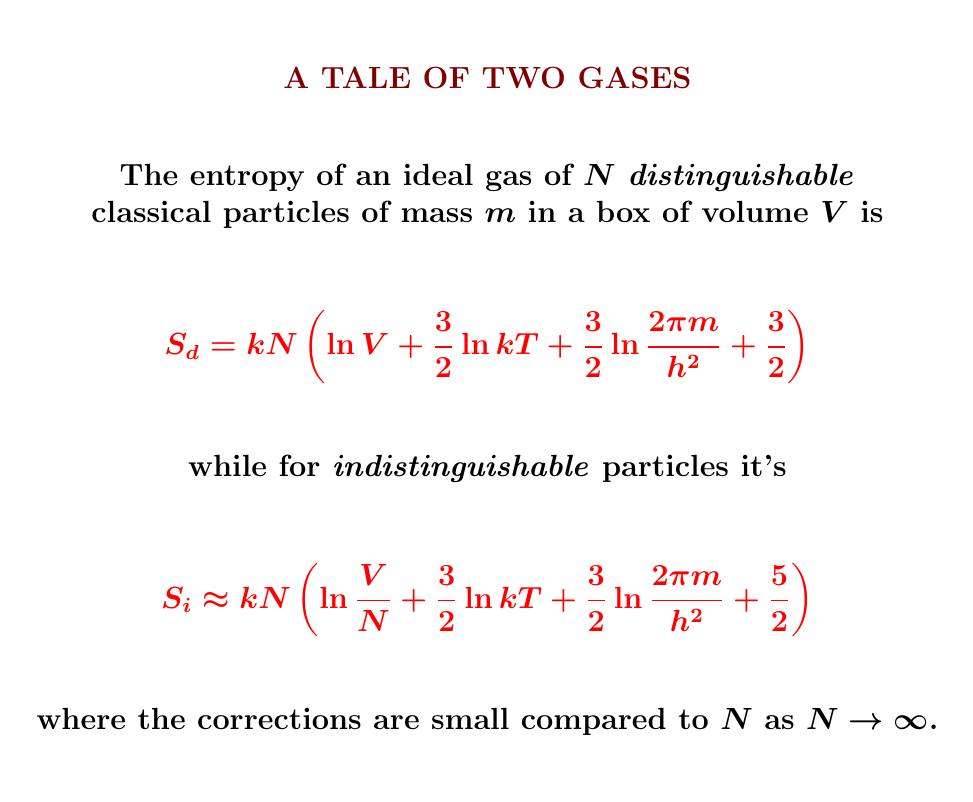
For distinguishable particles, the total entropy increases a lot when we open a tiny door connecting two boxes of gas - because it takes more information to say where each particle is. For indistinguishable particles, this doesn't happen!
Now let's see why.

The key to computing entropy is the partition function.
For \(N\) distinguishable particles, this is just the \(N\)th power of the partition function for one particle. For \(N\) indistinguishable particles, we also need to divide by \(N\) factorial.

Why is this?
For \(N\) distinguishable particles, the partition function is a product of \(N\) copies of the integral for one particle: our friend, the lonely particle in a 3d box.
For indistinguishable particles, we integrate the same symmetrical function over a space that's \(1/N!\) as big.

From the partition function we can compute the expected energy in the usual way. Here we get the same answer for distinguishable and indistinguishable particles!
Indeed, we can get this answer from the equipartition theorem. But I'll just remind you how it works:

From the partition function we can also compute the free energy. Here the two gases work differently!
Since the partition function for the indistinguishable particles is \(1/N!\) times as big, their free energy is bigger by the amount \(kT \ln N!\)

As usual, from the expected energy and free energy we can compute the entropy.
As you'd expect, the gas of indistinguishable particles has less entropy: \(k \ln N!\) less, to be precise. Permuting the particles has no effect — so they take less information to describe!

Finally, we can use Stirling's formula to approximate \(\ln N!\).
This gives a wonderful approximate formula for the entropy of an ideal gas of indistinguishable particles. In this approximation, doubling \(V\) and \(N\) doubles the entropy. But we can be more precise if we want!

And so this course is done. 'Twas fun!
Or almost done:
There's an open-book final for all of us! We can now compute the entropy of helium, and with a bit more work solve the mystery that got us started.


Another painting by Édouard
Cortès. This is one of the Rue de Lyon. So luminous!
October 23, 2022
If you turn a cube inside out like this, you get a shape called a rhombic dodecahedron. It's great — there's a lot to say about it. But if you do the analogous thing in 4 dimensions you get something even better: a 4d Platonic solid called the 24-cell!
The 24-cell has 16 corners at those of the original hypercube: $$ (\pm \textstyle{\frac{1}{2}}, \pm \textstyle{\frac{1}{2}}, \pm \textstyle{\frac{1}{2}}, \pm \textstyle{\frac{1}{2}}) $$ plus 8 more from turning it inside out: $$ (\pm 1,0,0,0) $$ $$ (0,\pm 1,0,0) $$ $$ (0,0,\pm 1,0) $$ $$ (0,0,0,\pm 1) $$ Its faces are regular octahedra — one for each square in the original hypercube.
We can fill 3d space with rhombic dodecahedra! Start with a cubic lattice with every other cube filled, and then 'puff out' the filled cubes until they become rhombic dodecahedra. They completely fill 3d space, forming the rhombic dodecahedral honeycomb:
Similarly, we can fill 4d space with 24-cells. We can do this the same way: take a hypercubic lattice with every other hypercube filled in, and then 'puff out' those filled-in hypercubes until they become 24-cells that fill all of 4d space. We get something called the 24-cell honeycomb.