diary - January 2023

Young foxes can be incredibly cute. I got this picture from the Fox Bot on Mastodon.

January 7, 2023

When I have insomnia I often visualize shapes. There's one I made up that I'd like to really see.

Start with the 'square antiprism' shown above. It has a square on top, a square rotated 45° on the bottom, and 8 equilateral triangles around the sides. Then put a pyramid on top — formed by 4 more equilateral triangles — and a pyramid on the bottom. You get a polyhedron with 16 equilateral triangle faces. Can you visualize it?

First, you can do something very similar starting with the 'pentagonal antiprism' shown here:

This has a regular pentagon on top and bottom, and 10 equilateral triangles around the sides. Now you put a 5-sided pyramid on top, formed by 5 equilateral triangles, and another one on the bottom. This gives a regular icosahedron!

What's nice here is that the same number of equilateral triangles meet at each vertex. So, it's a Platonic solid. The shape I'm thinking about is a kind of ugly parody, because some vertices have 4 equilateral triangles meeting there while others have 5.

This is roughly a square antiprism with a square pyramid on top. But it's missing the square pyramid on bottom. And the square on the bottom here is smaller than the square on top. That's because the atoms want to be roughly the same distance from their neighbors.

You can also see an atom in the middle! An atom of rhenium will surround itself with 9 hydrogens in approximately this way, forming the ion $\textrm{ReH}_9^{--}$. It's an unusual sort of ion. But actually people argue about whether its geometry is modeled after a 'capped square antiprism' or a 'tricapped trigonal prism', which gives a similar arrangement of 9 atoms around a central atom:

It's also called a 'tetrakis square antiprism', or a 'heccaidecadeltahedron'. The awkward names fit its awkward shape. It looks like an icosahedron that went on a diet and lost too much weight. It's one of the 92 'Johnson solids': strictly convex polyhedra with regular polygons as faces that do not have enough symmetry to map each vertex to any other.

January 8, 2023

We're in our salad days! In southern California, growing arugula in your yard is not hard. After enough rain it just shoots up! And it's been raining a lot lately.

Read my May 1st, 2020 entry for more about edible wild plants. I think a lot of people are missing a lot of fun by not finding out which weeds in their yard are edible.

January 10, 2023

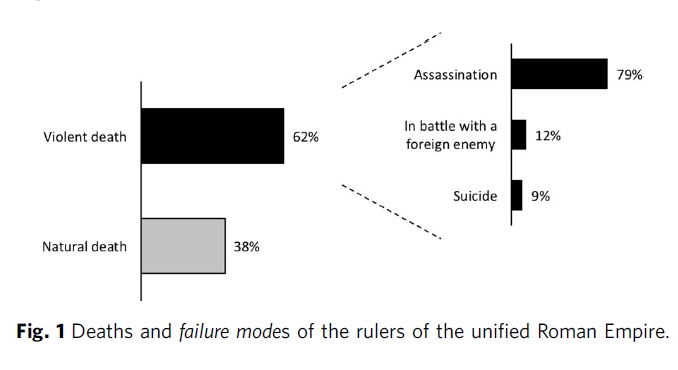
Being a Roman emperor was a very dangerous job: 62% of them met violent deaths! But this paper digs in and studies this scientifically:

Is a product especially likely to break the first few times you use it? Does it work for a while but then wear out? Or does it have a constant failure rate? Saleh studies this for Roman emperors.

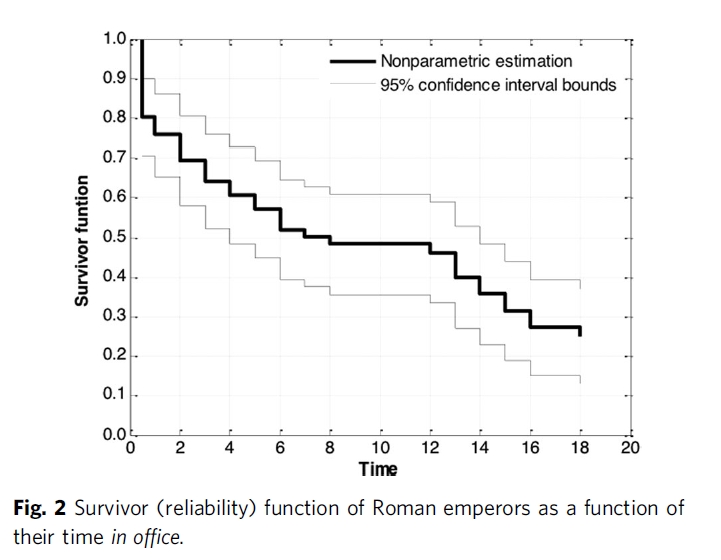
Roman emperors faced a high risk of violent death in their first year of rule. In reliability engineering this phenomenon is called 'infant mortality': a lot of products break early on.

But not for long: their risk of violent death rises again after 12 years! This is called a 'wear-out period' in reliability engineering: products also break when they get too old.

Reliability engineers study the 'survivor function' S(t): the fraction of products that survive up to time $t$. They often try to fit this to a 'Weibull distribution': $$ S(t) = \exp(-(t/T)^p) $$ for some time $T$ and power $p$.

$p \lt 1$ is good for fitting a survivor function with infant mortality. $p \gt 1$ is good for describing a wear-out period. But when there's both, reliability engineers often use a linear combination of two Weibull distributions. So Saleh does this for Roman emperors.

The 'hazard function' describes the failure rate per time per item that survives up to that time. Saleh graphs this for Roman emperors. We can clearly see there's both 'infant mortality' and something like 'wear-out'.

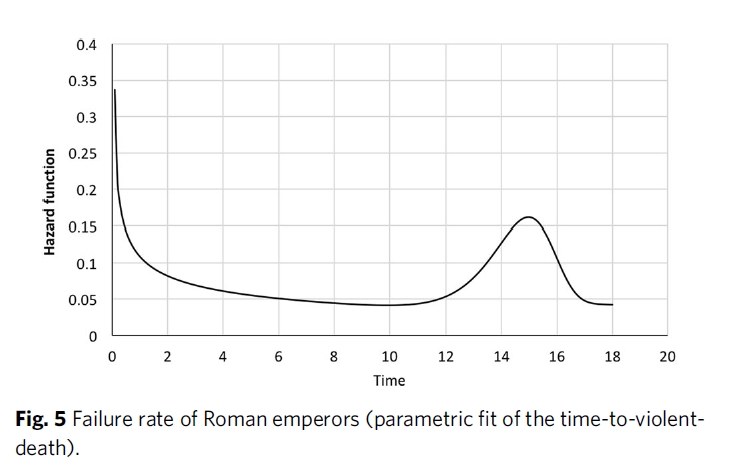
But is a linear combination of Weibull distributions really a principled way to fit this sort of data?

January 17, 2023

When I started at C# and included the white keys F and C I got an Ionian mode, otherwise known as a major scale, namely C# major. I probably knew this, but mainly it just sounded good.

When I started at C# and included the white keys E and B, I got a much more mysterious sounding scale. This turns out to be C# Dorian. This was one of my favorites, but I overused it so much that I find it a bit tough to take now. Sort of like a favorite spice that you used to put on every dish, until you got sick of it.

When I started at C# and included the white keys F and B, I got C# Mixolydian. I used this one less, but now I think it's very nice and subtle.

I didn't know much about modes back then, so I didn't even know I was playing Mixolydian, but now I know Mixolydian is one shade 'brighter' than Dorian and one shade 'darker' than the major scale (which is also called Ionian). If you don't know about this stuff, you might try my November 1st, 2022 diary entry.

There's one more possibility like this: when you start at C# and include the white keys E and C, you get C# melodic minor ascending.

I think this was my least favorite, perhaps because the minor key felt too much like it was 'tugging at my heartstrings' — though you can play in minor in ways that aren't sentimental.

Anyway, now that I'm learning a bit of music theory I can analyze what I used to do, starting with these simple tricks and working on up. It's fun!

January 18, 2023

Here Aimee Nolte shows us some ways we can stack a triad on top of the dominant 7th chord, which is

For example, the one I just explained stacks an A major triad on the C7 chord and gives us the C dominant 13 flat 9 or "C13♭9" chord.

But she rules out the triads that include the 4 or 7, or more precisely the notes an octave higher than those, the 12 and 15. The first is a minor 9th above our 3, the second a minor 9th above our ♭7. The minor 9th is dissonant!

Being a bit rebellious, I want to practice all ways of stacking a triad on top of a dominant 7th chord, including the dissonant "no bueno" ones. I might decide I like those dissonant ones... or maybe not.

Upper Structure	LH	RH	RH Triad	Chord Name
USII	E B♭	D F# A	E♭	C7#11
US♭III	E B♭	E♭ G B♭	E♭	C7#9
US♭V	E B♭	D♭ G♭ B♭	G♭	C7♭9#11
US♭VI	E B♭	E♭ A♭ C	A♭	C7#9♭13
USVI	E B♭	A C# E	A	C7♭9 13
USIm	E B♭	E♭ G C	Cm	C7#9
US♭IIm	E B♭	F♭ A♭ D♭	D♭m	C7♭9♭13
US♭IIIm	E B♭	E♭ G♭ B♭	E♭m	C7#9#11
US#IVm	E B♭	C# F# A	F#m	C7♭9#11
USVII	E B♭	F B♭ D	B♭	C7sus

These chords have standard names in jazz, which are listed under Upper Structure. For example the first is USII, meaning an upper structure chord where we stack a major II on the dominant 7th. If you know what you're doing, these names are enough to reconstruct the chords!

The column LH say what the left hand plays if you're using the key of C. Here, unlike in Aimee Nolte's video, the left hand always plays a 'rootless' voicing of the dominant 7th. That, instead of playing the dominant 7th in its original form:

The column RH says what the right hand plays. It's always a triad, which is shown under RH Triad. So RH Triad gives a compressed version of the same information, and a good musician would probably prefer this compressed form.

You may wonder why the chords are listed in the order they are. It's not random! The chords with major triads are listed first, then the chords with minor triads, and finally one with a diminished triad: USVII.

These chords also have other names, which are listed under Chord Name. These names include the key the chord is played in: for simplicity they're listed here in the key of C. Here USII is also called C7#11, because it's a dominant 7th with a 9th and a sharped 11th stacked on top. The 9th is left unspoken here: we could call this chord C79#11 but people consider that notation inefficient. But the 9th were sharped or flatted, we need to mention it. For example US♭V is C7♭9#11.

I find these other names confusing, because they're not completely logical and people seem to use different conventions. I've gotten the names from this page:

but other names seem more common. For example, the USVI chord, which I discussed at length above, is usually called C13♭9, but this page calls it C7♭9. That makes no sense to me since it omits the 13. So was it a typo, or just a notation I don't understand? In an effort at logical consistency I made up a name I've never seen elsewhere: C7♭9 13. Please don't take this one seriously!

Do you know a really careful, detailed treatment of upper structure chords, with nice complete charts?

If you find this stuff intimidating or otherwise unpleasant, I recommend ignoring it and watching Aimee Nolte's video, since she derives the information in this list from first principles in a friendly commonsense way.

Alternatively, you can just sit down at a piano, play some of the chords, and enjoy how they sound. I'm nowhere near able to deploy these chords in improvisation, the way a good jazz musician could — mainly because I don't tend to improvise with dominant 7ths in the left hand. But at least I can play these chords and enjoy them! And I hope someday I'll incorporated them in my improvisations.

Aristotle claimed that identical regular tetrahedra could be packed in a way that fills space. It seems unlikely if you actually try it — but only in 1925 was it proved impossible. And only in 2010 did people prove a nontrivial upper bound on the density of the packing you can achieve, namely

On the other hand, the densest known packing has density about .8563 - there's a discussion here, and a picture, shown above:

But I'd hate to have to formalize it in a completely rigorous way, on a computer. (Some other people would enjoy that challenge.)

Here's the proof that no packing of equal-sized regular tetrahedra can have density more than $1−2.4 \cdot 10^{-25}$:

I hope someone improves this upper bound! I'll bet the true upper bound is ~0.8563. I'd be shocked but delighted if someone can beat this.

January 25, 2023

Take a box full of equal-sized regular tetrahedra. Start compressing it. These patterns tend to form!

ii has 9 tetrahedra: it's built by taking two copies of i and letting them share a single tetrahedron.

iii is made from 20 tetrahedra arranged in an icosahedral pattern. Again it has cracks.

This shows what can happen when you take a box of 8000 tetrahedra and compress it too rapidly for large-scale patterns to form! It got stuck at a density of 0.7858.

To reach a higher density, you need to compress the box more slowly and shake the tetrahedra around a bit. Below a box of 13824 tetrahedra was slowly compressed, reaching a density of 0.8324. The result is layered quasicrystal with approximate 12-fold symmetry! It's full of rings formed by interpenetrating tetrahelixes.

It's not just this one example, either. Repeated simulations show these structures tend to spontaneously form when a box of equal-sized regular tetrahedra is slowly compressed!

This is an interesting topic in statistical mechanics. For infinitely hard tetrahedra — or other shapes — the potential energy is infinite if they interpenetrate and zero otherwise. So all allowed configurations have zero potential energy! They can still have kinetic energy. But to minimize free energy $$ F = E - TS $$ at low temperatures, they will minimize kinetic energy and arrange themselves in a probability distribution of patterns that maximizes the entropy $S$.

If the density is high enough, hard shapes form patterns at low temperatures, even though they are maximizing entropy!

And as we reduce the density, there's a phase transition between an ordered state — like a crystal or quasicrystal — and a disordered state. This was first predicted by Onsager in 1949 for hard thin rods and by Kirkwood in 1951 for hard spheres. Tetrahedra are much more complicated.

For my December 2022 diary, go here.