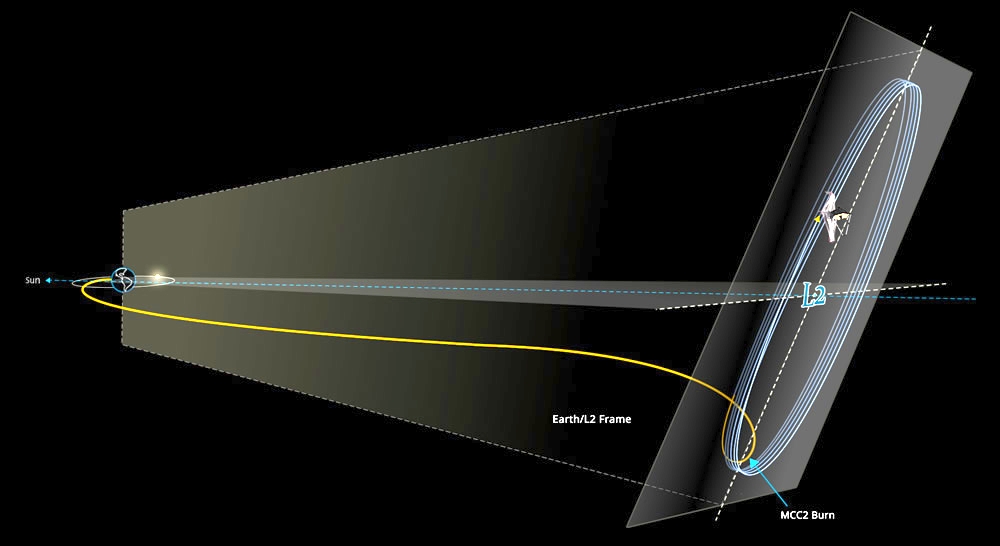

Yay! The James Webb Space Telescope is now orbiting the Earth-Sun Lagrange point L2. I think it's safe to talk about now.
L2 is an unstable point. So they'll need to use a little propellant every 3 weeks to keep the orbit from spiraling out.
Bot thrusters can only push the James Webb away from the Sun,
so if it had overshot L2 there would have been no way to
save it! And if they don't figure out how to refuel it or something,
when it runs out of propellant it'll drift away from L2.
With a bit of luck should do lots of great work before then.
February 2, 2022
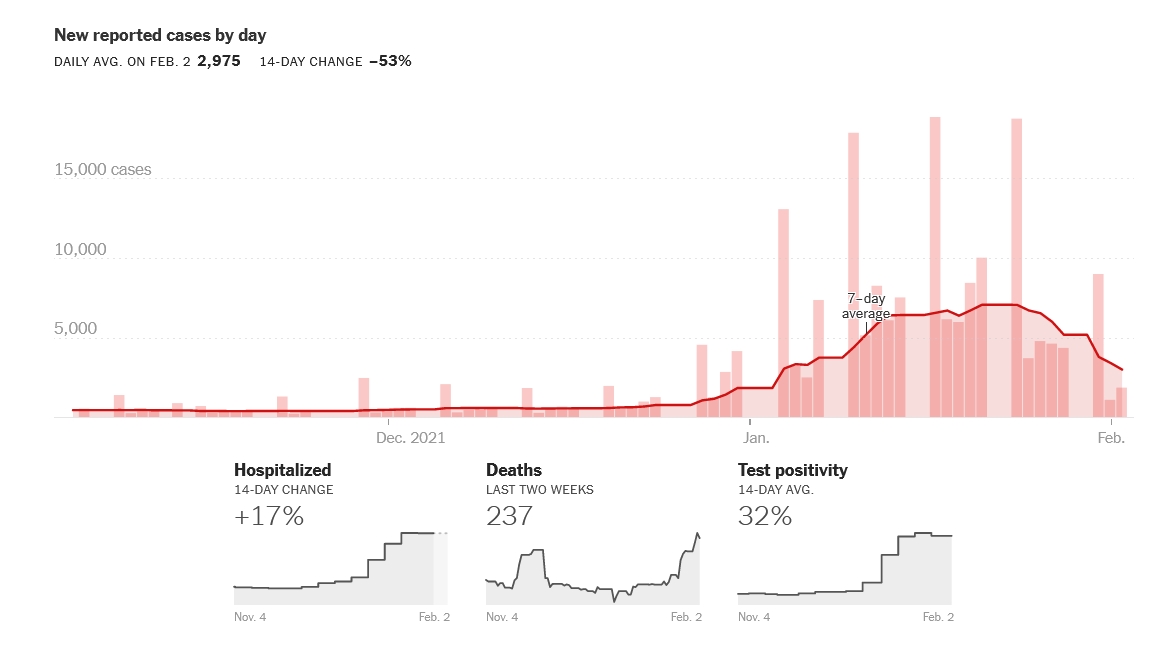
New cases of coronavirus in the county of Riverside California are dropping
as the omicron wave subsided.
February 3, 2022
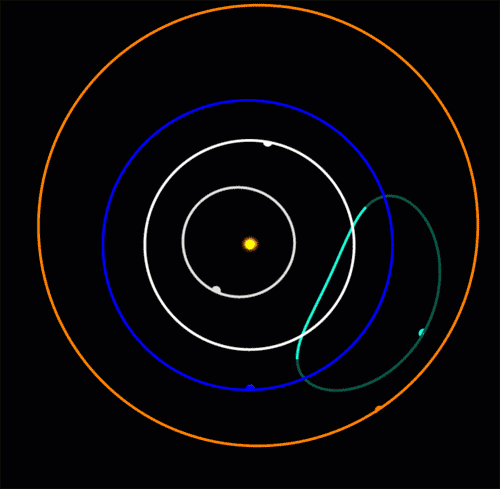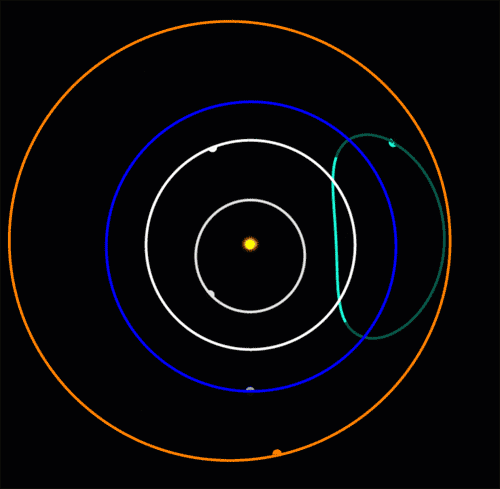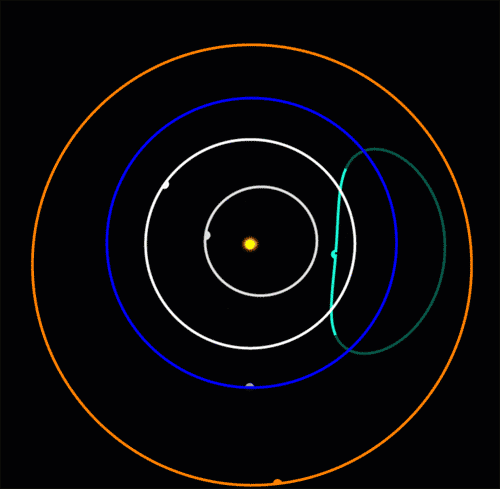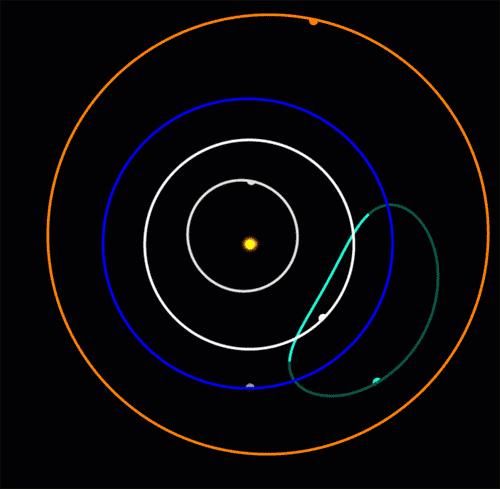
In 2020 astronomers discovered an 'Earth Trojan': an asteroid oscillating around Earth's Lagrange point L4. Earth is the blue dot at the bottom of the blue circle. This asteroid moves in a bean-shaped orbit that crosses the orbit of Venus. Venus is expected to destabilize it in 4000 years!
It's called 2020XL5 and it's only the second Earth Trojan to be discovered: the first was found in 2010.
Why are so few asteroids seen in the L4 and L5 points of Earth compared to Mars? We're farther from the asteroid belt, but the real reason is that the L4 and L5 points are just 60° from the Sun, so we mainly see the shadowed side of any asteroid there.
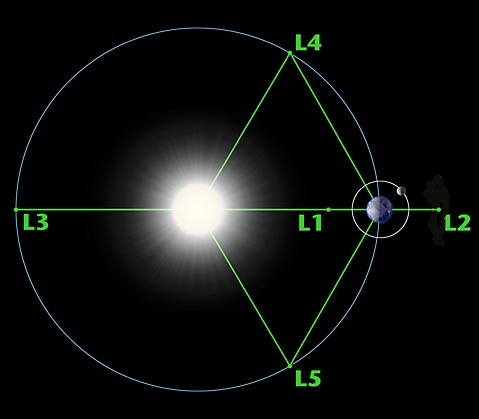
Also, to see them at night, they must be at least 30° away from the vertical, so we must look through quite a bit of atmosphere. To add to the difficulty, there is zodiacal light to contend with, caused by interplanetary dust in the plane of the Earth's orbit.
All this makes even more impressive that they spotted 2020XL5, which is just about 1 kilometer across! Here's the team that did it:
My favorite asteroid is 3753 Cruithne. Viewed in rotating coordinates where the Earth stays still, it traces out a complex path. But really it's orbiting the Sun in an almost elliptical orbit, slightly affected by the Earth.
Its orbit is tilted, so it's unlikely to hit us.
To see how complicated Cruithne's orbit is, you have to simulate it for a long enough time. Here Earth is a blue dot, wiggling in and out once each year. In this rotating coordinate system, Cruithne's orbit looks like a bean that moves back and forth!
But in a nonrotating coordinate system, Cruithne doesn't look so weird! In the short term, it moves in an ellipse tilted about 20° relative to the plane of Earth's orbit. Over the long term, this ellipse slowly precesses in complex ways.
When you view Cruithne's elliptical orbit in rotating coordinates where the Earth stands still, it looks like Cruithne moves in a bean-shaped orbit. Over the long term, this bean moves around as Earth's gravity affects Cruithne's orbit.
Each time Cruithne comes close to us, the Earth's path is deflected by about 1.3 centimeters, while Cruithne's path is affected more dramatically: the motion of the 'bean' reverses.
Its next close approach will be in 2292.
I got the first gif, and this one here, from Brad Snowder's astronomy pages at Western Washington University. Check out his explanations:
Imagine something orbiting the Sun like this. If it goes around once a year, it almost seems like it's orbiting the Earth! From our point of view, it goes around us once a year.
Such a thing is called a quasi-satellite. And Earth has at least 5 of them!
The Earth's first quasi-satellite was found in 2004. It's an asteroid that follows the red orbit here. It will not be a quasi-satellite forever! Calculations show that around 2600 it will switch to a 'horseshoe orbit' going around the Lagrange points L4 and L5. It's called 2005 GU9 and it's classified as potentially hazardous.
Here's what a quasi-satellite looks like it's doing from an Earth-centered viewpoint. It traces out a weird bean-shaped path. And it's 'retrograde' — it goes the opposite way from how the Earth goes around the Sun!
Venus has one known quasi-satellite, Neptune has one too, and even the asteroid Ceres may have one.
In 1989, the Russians made a spacecraft into a quasi-satellite of the Martian moon Phobos.
What's the difference between a quasi-satellite and a satellite in a large retrograde orbit? When the satellite gets so far from the Earth that it takes one year to orbit, is it a quasi-satellite? There are lots of interesting things to ponder here!
The last picture above is from here:
February 8, 2022
This is what new coronavirus cases looked like on January 25th:
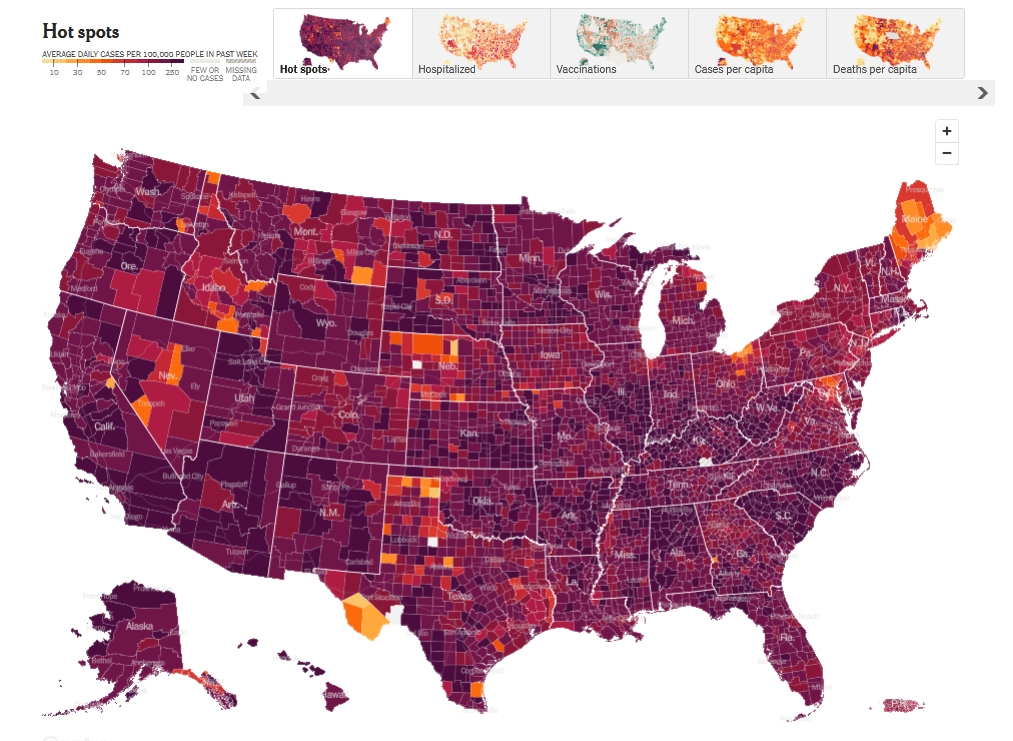
Here's what they look like today — much better. But we still
had 2594 deaths from this disease in the US today.
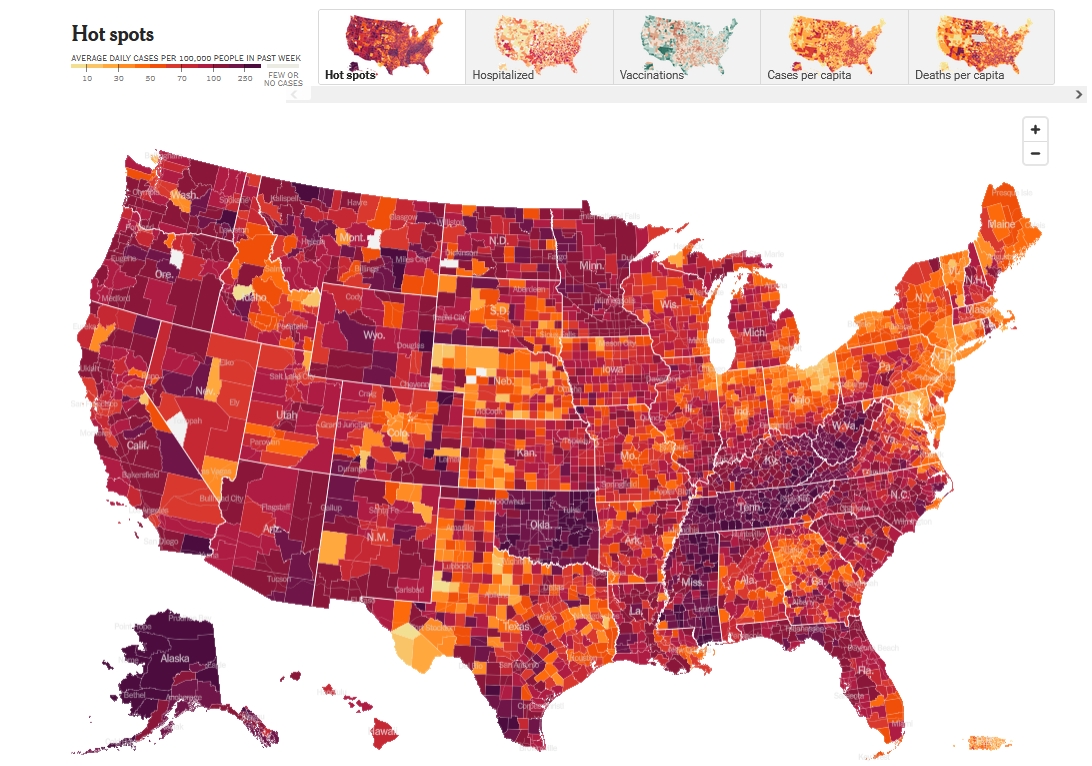
February 14, 2022
We're down to 2400 deaths today — slight
improvement — but cases are down much further.
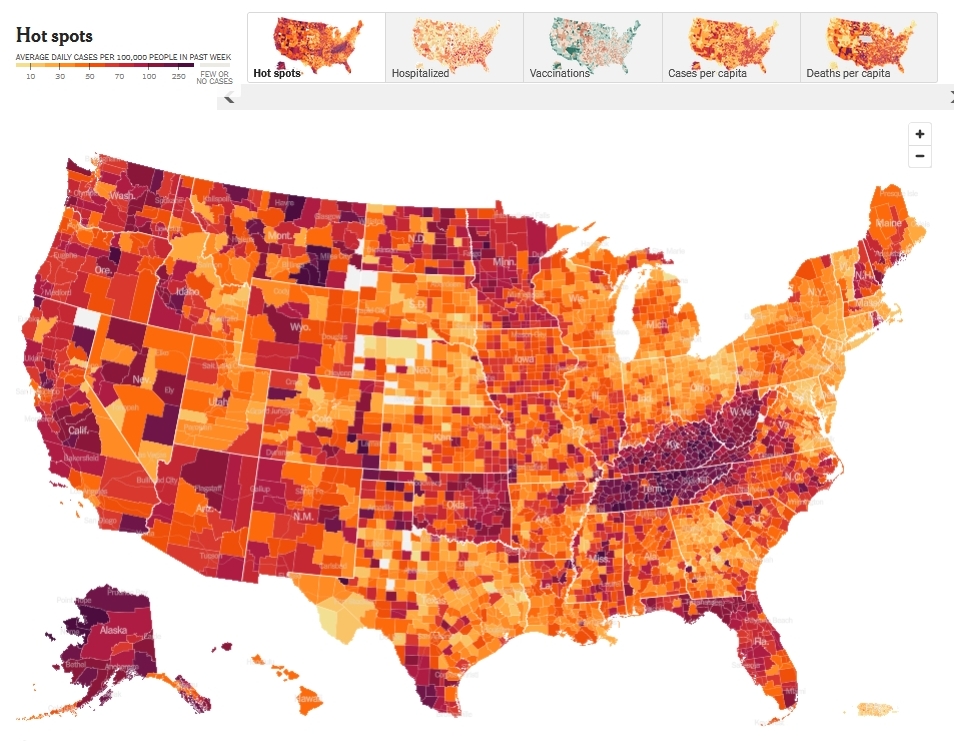
Looking ahead to the future, here's the map on March 6th:
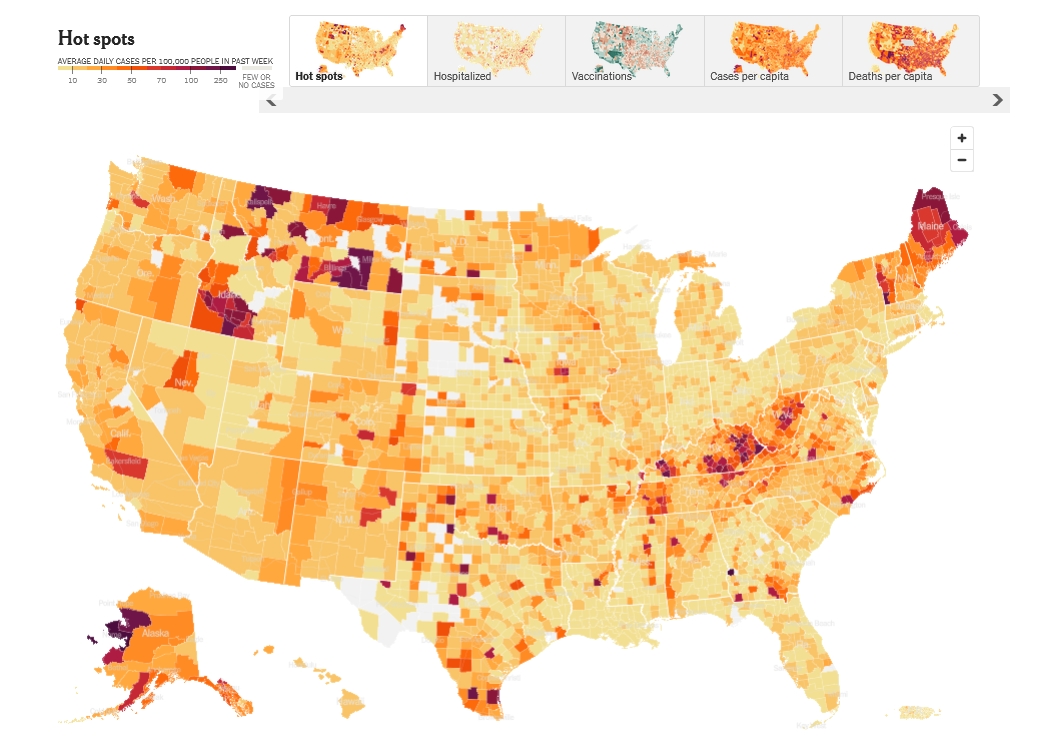
So it looks like this wave of the omicron variant is fading. What next,
I wonder?
February 18, 2022
A good mathematician should know lots of ways to turn things into
other things. They're called 'functors'. And whenever
you meet a new thing and have some functor you can apply to it, you
should give it a try.
Let me give some examples.
There's a functor that turns monoids into groups, called 'group completion'. For commutative monoids it gives a group where elements are formal expressions \([a] - [b]\) where \(a,b\) are in your monoid, obeying the rule $$ [a+c] - [b+c] = [a] - [b] $$ You saw two examples in school!
Take your monoid to be the natural numbers \(\mathbb{N}\), with \(+\) as its monoid operation. Then its group completion is the integers, \(\mathbb{Z}\).
Or take your monoid to be the nonzero integers, with \(\times\). Then its group completion is the nonzero rational numbers.
Thus numbers are born.
There's also functor that turns monoidal categories into monoids, called 'decategorification'. The elements of your monoid are isomorphism classes \([x]\) of objects \(x\) in your monoidal category, multiplied like this: $$ [x] [y] = [x \otimes y] $$ This too is something you've seen.
Take the monoidal category of finite sets, with disjoint union as the monoidal structure. Decategorify it! You get the monoid of natural numbers, with + as its monoid operation.
This is why we use natural numbers to 'count' — and why adding them is popular.
Or take the category of finite sets with cartesian product as its monoidal structure. Decategorify it, and you get the natural numbers with × as its monoidal structure.
So to count the elements of a cartesian product of two finite sets, you can just count each one and then multiply.
So we have two functors that we can compose: $$ \textrm{decategorification}: \textrm{monoidal categories} \to \textrm{monoids} $$ $$ \textrm{group completion}: \textrm{monoids} \to \textrm{groups} $$ and applying them to the category of finite sets with disjoint union we get the integers with addition!
But we can do more with them....
Let \(G\) be a finite group. Let \(\mathrm{Rep}(G)\) be the category of its finite-dimensional, complex representations, with the usual direct sum \(\oplus\) of representations as its monoidal structure. Decategorify it! You get the 'representation rig' of \(G\).
But wait, we're not done...
The representation rig is a monoid, so we can group complete it and get the representation ring \(R(G)\). This is more famous, and very useful.
By design we can add things in \(R(G)\), but the tensor product \(\otimes\) of representations also lets us multiply, so it's a ring.
Theorem. \(R(G)\) tensored with the complex numbers is isomorphic to the ring of complex functions on G that are constant on each conjugacy class, with the usual \(+\) and \(\times\) of functions.
This lets us work concretely with \(R(G)\) and prove tons of stuff about group representations!
This trick is used all over math. For example, 'K-theory' is another example of turning a monoidal category into a group in two steps. We start with the category of vector bundles over a topological space \(X\), with \(\oplus\) as its monoidal structure, and get a group called \(K(X)\), the K-theory of \(X\)
Learning the general tricks makes such examples much less
intimidating. Functors are fun!
February 19, 2022
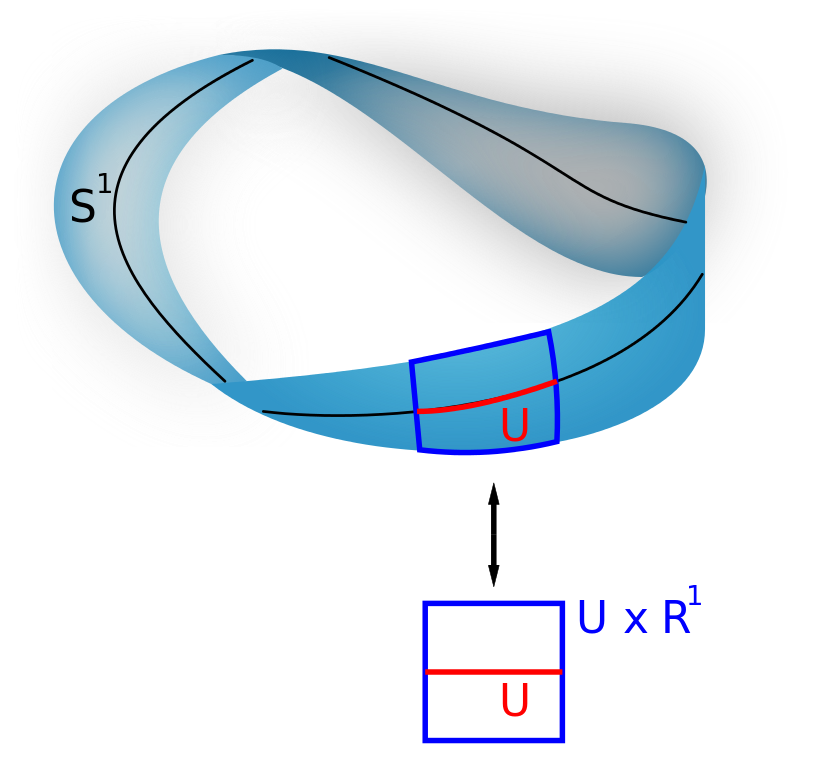
Very roughly, a line bundle over a space \(X\) is a space that's made of lines, one for each point in \(X\). For example, a Möbius strip can be seen as a line bundle over the circle \(S^1\).
To make this a bit more precise: in this game a line is a 1-dimensional vector space. The Möbius strip is a 'real line bundle' since its lines are 1d vector spaces over the real numbers. There are also 'complex line bundles', like the tangent bundle of the sphere \(S^2\):

Yes: while ordinary nerds talk about the 'complex plane', supernerds call it the 'complex line', since the complex numbers form a 1-dimensional vector space over \(\mathbb{C}\). People think a lot about complex line bundles because they're really nice.
If you pick your favorite field you get a category of lines, with 1d vector spaces as objects and linear maps as morphisms. And the cool thing is that you can multiply lines and get a line, using the tensor product of vector spaces. So this category is monoidal!
There's also a category of real line bundles over any fixed topological space X. And this category is monoidal, thanks to our ability to tensor lines! So I can ask you: what happens when you tensor the Möbius strip with itself?
Yes, you can square the Möbius strip!
You can prove that since the Möbius strip has a single twist, its square has a double twist. But a line bundle over the circle with a double twist is isomorphic to one with no twist at all! So the square of the Möbius strip is just the 'trivial' line bundle, or cylinder!
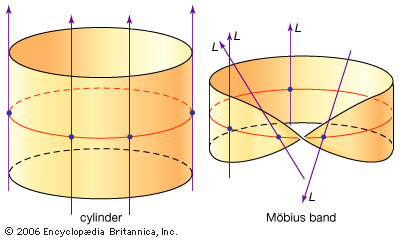
More precisely, the square of the Möbius strip is isomorphic to the trivial line bundle. To count isomorphic line bundles as equal, we should take our category of line bundles and hit it with a functor I explained in my February 18th entry: 'decategorification'.
If we take the monoidal category of real line bundles on the circle and decategorify it, we get a monoid with just two elements: \(M\) from the Möbius strip and 1 from the cylinder. And in this monoid we have $$ M^2 = 1 $$ Yes, it's our friend: the group with two elements!
In fact whenever you decategorify the monoidal category of real line bundles over a space \(X\), the resulting monoid is a group! The reason: for any line \(L\), its dual \(L^\ast\) is naturally its inverse: there's a natural isomorphism $$ L \otimes L^\ast \cong \mathbb{R} $$
Any line bundle \(E\) gives a line bundle \(E^\ast\), which we get by replacing each line in \(E\) by its dual vector space, and $$ E \otimes E^\ast \cong 1 $$ where \(1\) means the trivial line bundle. So when we decategorify the monoidal category of line bundles over a space \(X\), we get a group!
This trick for getting a group works for both real and complex line bundles, and it works in many contexts. People love to do it for holomorphic complex line bundles over complex manifolds! And then this group is called the Picard group of our complex manifold.

For example, the 2-sphere is a complex manifold which nerds call the Riemann sphere, and supernerds call the complex projective line — and its Picard group is \(\mathbb{Z}\), the integers! And in this group, the tangent bundle gives the element 2. Yes, the tangent bundle is the square of some other complex line bundle!
There's a ton more to say about this. I'd really like to explain a
lot of stuff I'm learning about Picard groups — it's so cool! But
it's time for me to get up and make breakfast.
February 21, 2022
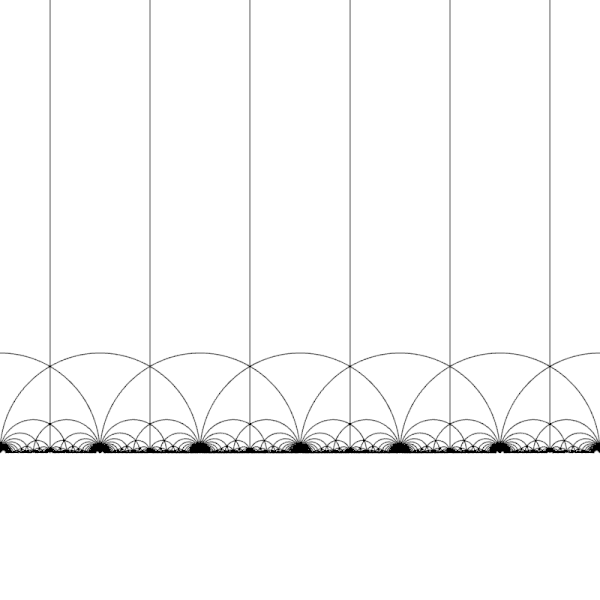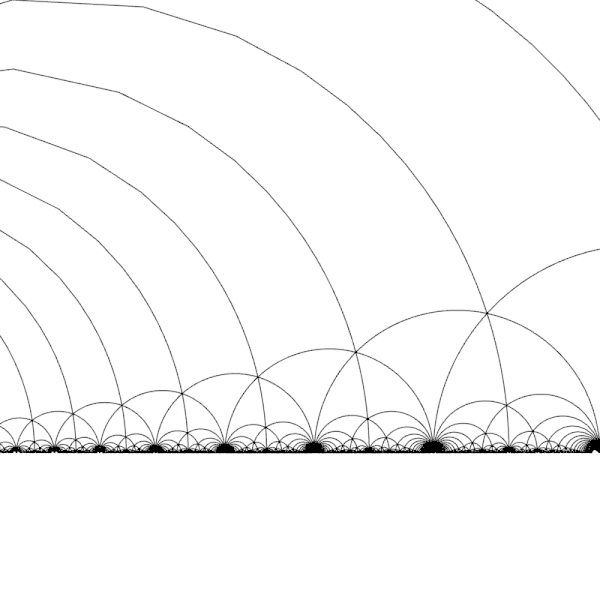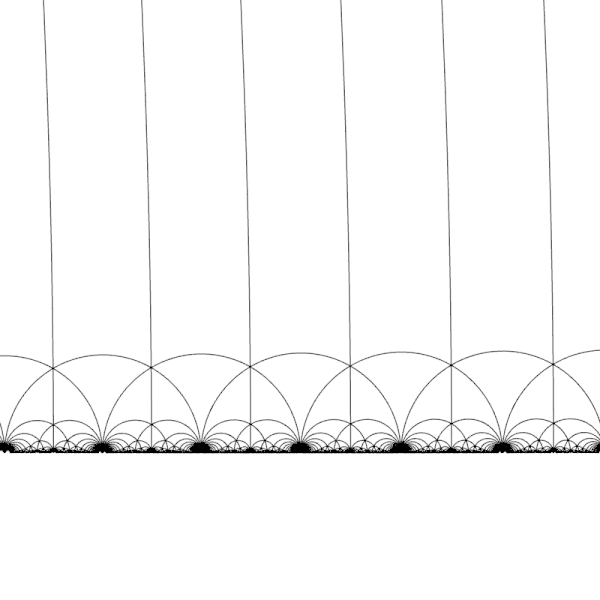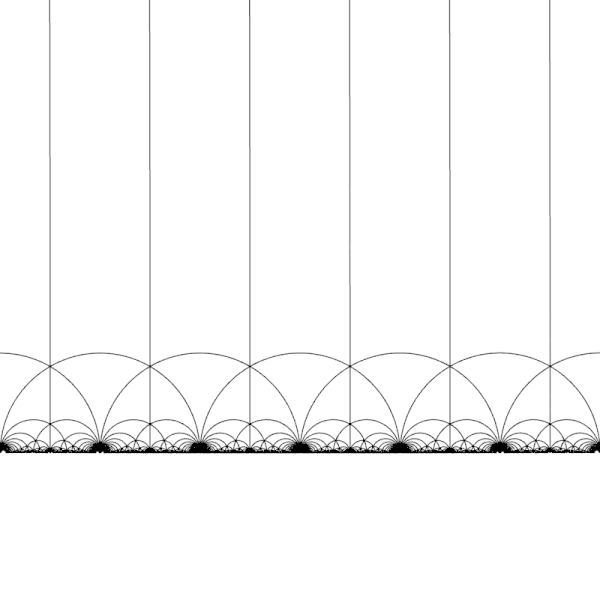
The modular
group consists of transformations
$$ z \mapsto \frac{az + b}{cz + d} $$
where \(a,b,c,d\) are integers with \(ad-bc = 1\). It's generated by
the transformations
$$ T(z) = z + 1 $$
and
$$ S(z) = -1/z $$
It acts on the upper half-plane, and starting from points in the
shaded region you can get to every point in the upper halfplane using
a unique element of the modular group:
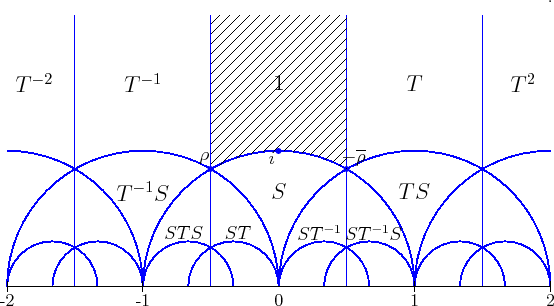
So, we say the shaded region is a 'fundamental domain' for the modular group's action on the upper half-plane. It has sharp corners or 'cusps' at the cube root of unity \( \rho = e^{2 \pi i / 3}\) and the sixth root \( -\overline{\rho} = e^{\pi i/ 3} \).
I guess \(T\) stands for 'translation'. The transformation $$ T(z) = z + 1 $$ shifts everything over to the right:

But why is the modular group important?
Here's one reason: any point in the upper half-plane determines an 'elliptic curve', and two points give the same elliptic curve if and only if they're related by the modular group! For a great visual introduction to how this works — without an explanation of elliptic curves, but they're lurking in the background — see Simon Burton's tweet series.
For more details, start here: