_tiling.png)
More precisely you get the complex version of the Bolza curve, with its correct conformal structure, by gluing together opposite sides of this patch of the hyperbolic plane:
The symmetry group of the Bolza curve has 48 elements: it's \(\mathrm{GL}(2,3)\), the group of \(2 \times 2\) invertible matrices with entries in the field with 3 elements. This is a double cover of the rotational symmetry group of the octahedron!
So let's build the Bolza curve from an octahedron.
Take \(y^2 = x^5 - x\) and try to solve for \(y\): $$ y = \sqrt{x^5 - x} $$ This is two-valued so we get a branched double cover of the sphere, with branch points where \(x^5 - x\) is zero or infinity.
And where are those points?
They're the vertices of an octahedron!
This branched double cover of the sphere is the Bolza curve. You might think it has the same symmetry group as an octahedron, given how we built it. But because of the double cover business its symmetries give a double cover of the octahedron's rotational symmetry group!
The octahedron has \(4! = 24\) rotational symmetries since you can permute its 4 pairs of opposite faces any way you want. This group has two different nontrivial double covers: the 'binary octahedral group' and the symmetry group of the Bolza curve.
You can see these two double covers if you know about the 'pin groups'. The orthogonal group \(\mathrm{O}(n)\) has two different nontrivial double covers called the pin groups \(\mathrm{Pin}^+(n)\) and \(\mathrm{Pin}^-(n)\). The octahedron's rotational symmetry group \(S_4\) sits in O(4) since you can permute the coordinate axes — so \(S_4\) gets two double covers coming from the two Pin groups, and these are in fact nonisomorphic 48-element groups.
It's a bit sad that the symmetry group of Bolza's curve is not the binary octahedral group, but instead the other double cover of \(S_4\). But don't blame me: I'm not the one making these decisions.
There's lots more cool stuff here:
People usually don't say "double cover", even though it's true: they say "central extension by \(\mathbb{Z}/2\)". \(S_n\) has two called \(2 \cdot S_n^+\) and \(2 \cdot S_n^-\), and when \(n = 4\) both are somewhat famous:
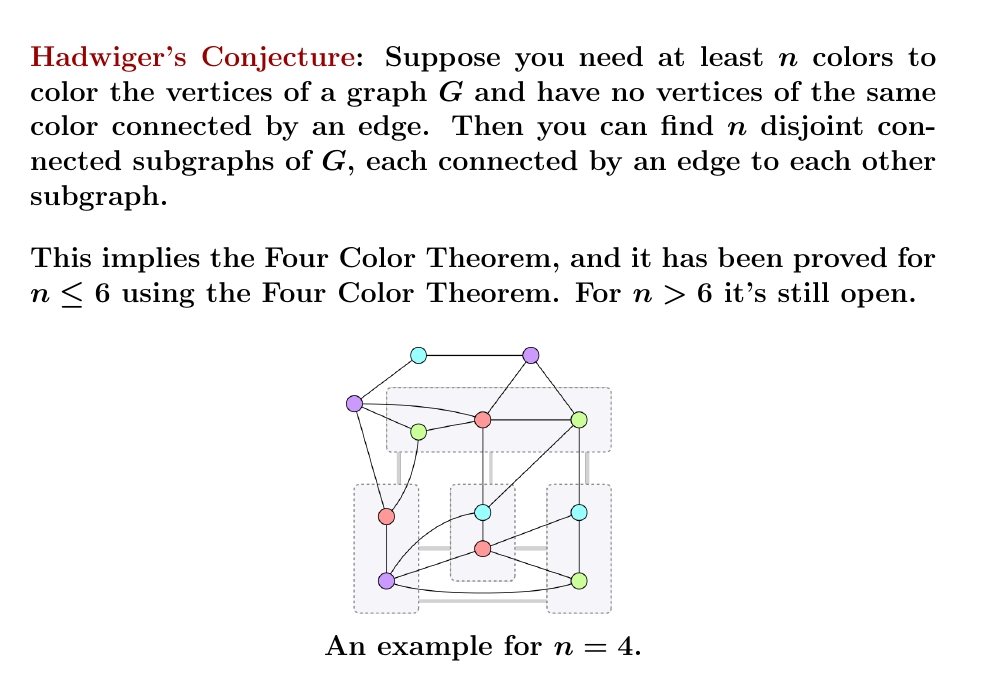
Whoa! I just learned that the Four Color Theorem, so far proved only with help from a massive computer calculation, follows from an even harder conjecture that's still unproved! And this harder conjecture is very nice and easy to state.
The picture above shows an example. You need at least 4 colors to color the vertices of this graph with no two of the same color connected by an edge. Hadwiger's conjecture says this graph must have 4 connected subgraphs, each connected to every other with an edge. And it does!
Hadwiger made this conjecture in 1943 and proved it for \(n \le 4\). For \(n = 5\) it implies the Four Color Theorem: it says a graph that needs \(5\) colors has \(5\) connected subgraphs all connected to each other by edges, and this implies it's not planar.
For \(n = 5\) it looks stronger than the Four Color Theorem but Wagner showed in 1937 that this case follows from the Four Color Theorem.
In 1993 Robertson, Seymour and Thomas showed the \(n = 6\) case also follows from the Four Color Theorem.
The \(n = 7\) case and all higher cases are still open! But it's known exceptions to Hadwiger's conjecture, if they exist at all, are rare:
What a great problem! Prove it in an elegant way, and you'd have a better proof of the Four Color Theorem.
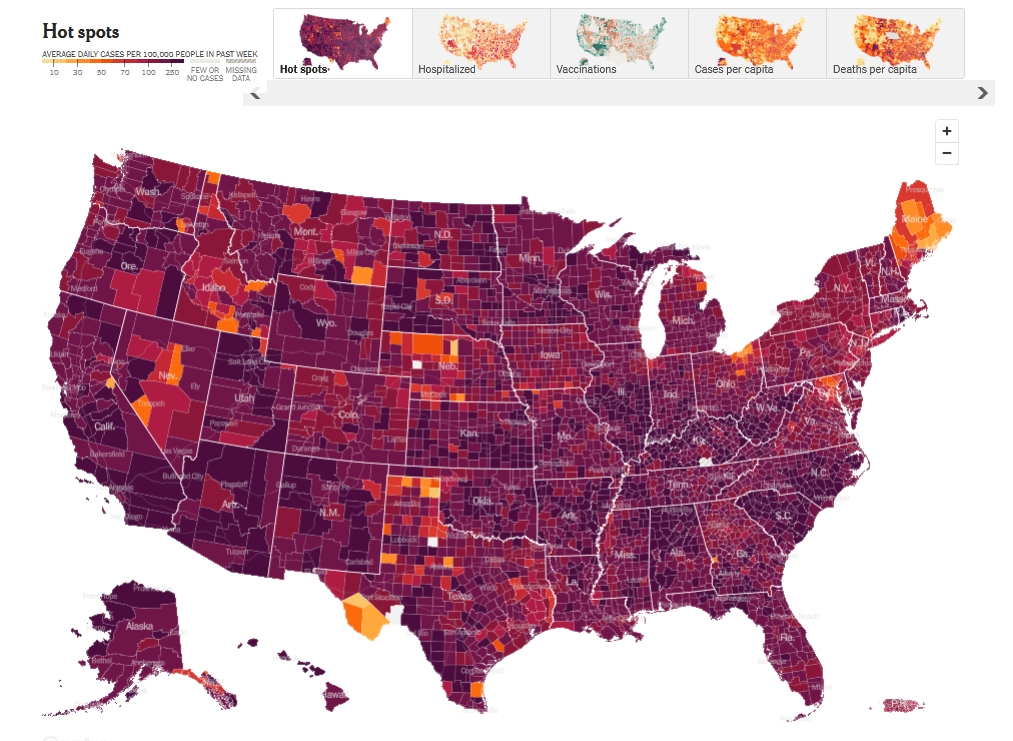
Cases of coronavirus are spiking again in the United States due to the
new highly transmissible omicron variant, starting in big cities like
New York and DC and quickly spreading over the whole country. I haven't
been talking about it because we're all used to it by now, but it's worse
than ever. Lisa and I socialize with just a few select friends.
January 11, 2022
Przybylski's star. Almost no iron in its atmosphere. Instead: rare
earth metals... and even radioactive elements like plutonium, curium,
einsteinium! It's so weird some astronomers have wondered if it's a
nuclear waste dump for an alien civilization.
The problem is, how do you get a lot of short-lived radioactive elements into the upper atmosphere of a big hot star? They're usually formed by merging neutron stars. So I'll make my own wacky guess: Przybylski's star zipped through the remains of such an event. Or maybe it was part of a ternary star system, and two of its partners became neutron stars, merged, and fell into it.
These are some other guesses people have made:
Sagan, Shklovskii and Drake once suggested that aliens could announce
their presence by dumping lots of a weird element like promethium into
a star. So it's ironic that now that we see a star with promethium in
it, few believe it's due to aliens.
January 13, 2022

This is the color of something infinitely hot. Of course you'd instantly be fried by gamma rays of arbitrarily high frequency, but this would be its spectrum in the visible range.
This is also the color of a typical neutron star. They're so hot they look the same.
This was worked out by David Madore.
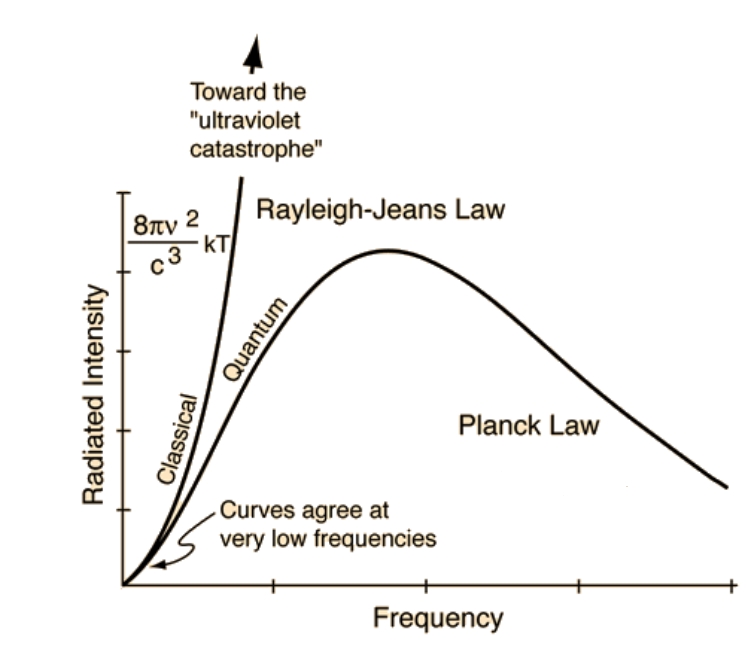
As a blackbody gets hotter and hotter, its spectrum approaches the classical 'Rayleigh–Jeans law'. That is, its true spectrum as given by the 'Planck law' approaches the classical prediction over a larger and larger range of frequencies.
So, for an extremely hot blackbody, the spectrum of light we can actually see with our eyes is governed by the Rayleigh–Jeans law. This law says the color doesn't depend on the temperature: only the brightness does!
And this color is shown above. This involves human perception, not just straight physics. So David Madore needed to work out the response of the human eye to the Rayleigh-Jeans spectrum — "by integrating the spectrum against the CIE XYZ matching functions and using the definition of the sRGB color space."
The color he got is sRGB(148,177,255). And according to the experts who sip latte all day and make up names for colors, this color is called 'Perano'. So we can say that Perano is the color of infinite hotness.
Here is some background material Madore wrote on colors and visual perception. It doesn't include the whole calculation that leads to this particular color, so somebody should check it, but it should help you understand how to convert the blackbody spectrum at a particular temperature into an sRGB color:
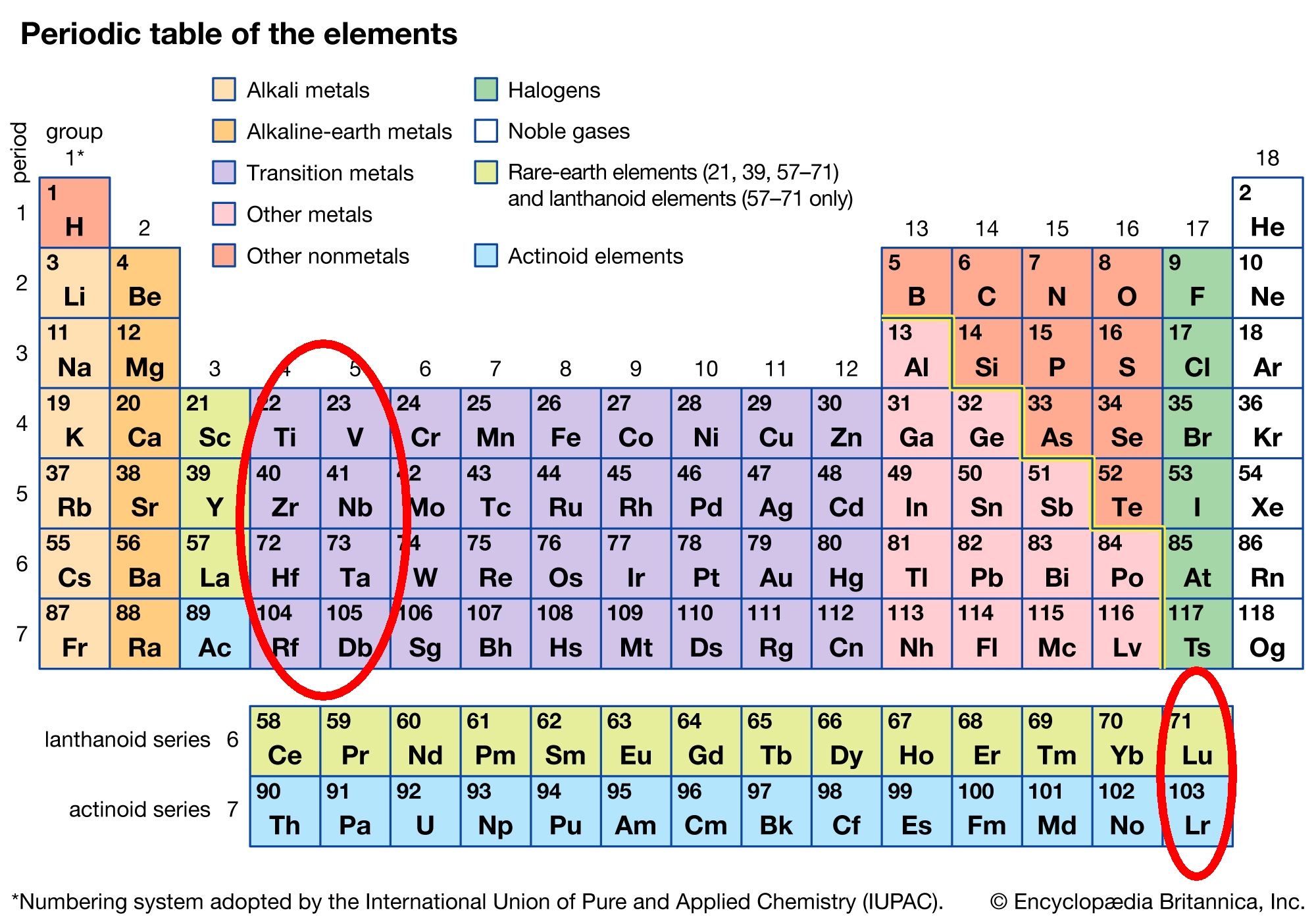
I like many kinds of periodic table, but hate this one. See the problem? Element 57 is drawn right next to element 72, replacing the element that should be there: element 71. So lutetium, element 71, is being denied its rightful place as a transition metal and is classified as a rare earth. Meanwhile lanthanum, element 57, which really is a rare earth, is drawn separately from all the rest! This is especially ironic because those rare earths are called 'lanthanoids' or 'lanthanides'.
Similarly, element 89 is next to element 104, instead of the element that should be there: element 103. So lawrencium, element 103, is also being denied its rightful place as a transition metal. Meanwhile actinium, element 89, is banished from the row of 'actinoids', or 'actinides' — even though it gave them their name in the first place. How cruel!
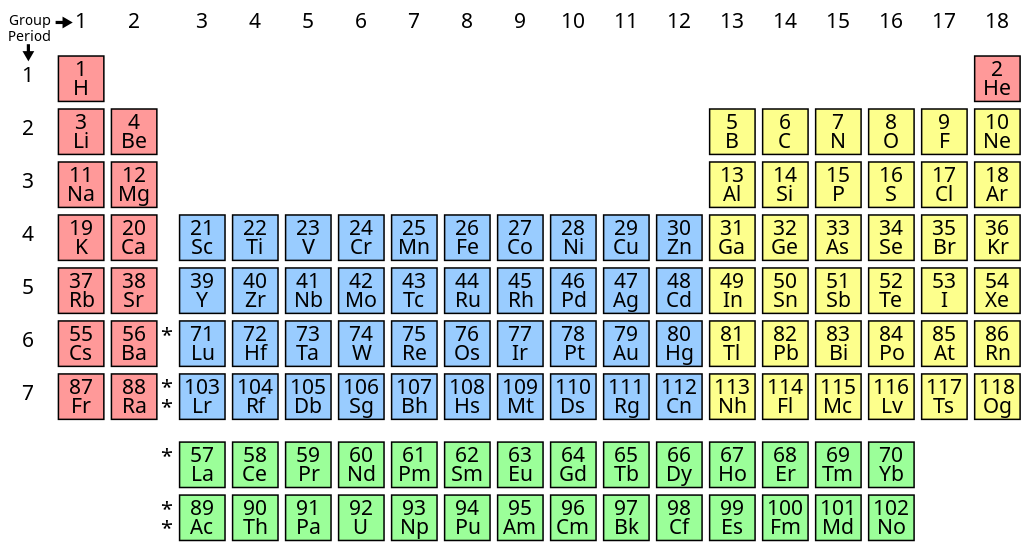
Here Wikipedia does it right. Element 71 is a transition metal — not element 57. Similarly element 103 is a transition metal, not element 89.
This stuff is not just an arbitrary convention. Transition metals are chemically different from lanthanides and actinides. You can't just stick them wherever you want.
In simple terms, as we move across the transition metals, they fill 1, 2, 3, ... , 10 of their outermost p orbitals with electrons. Similarly as we move across the lanthanides or actinides, they fill 1, 2, 3, ... 14 of their outermost d orbitals with electrons. I wrote about this a while ago:
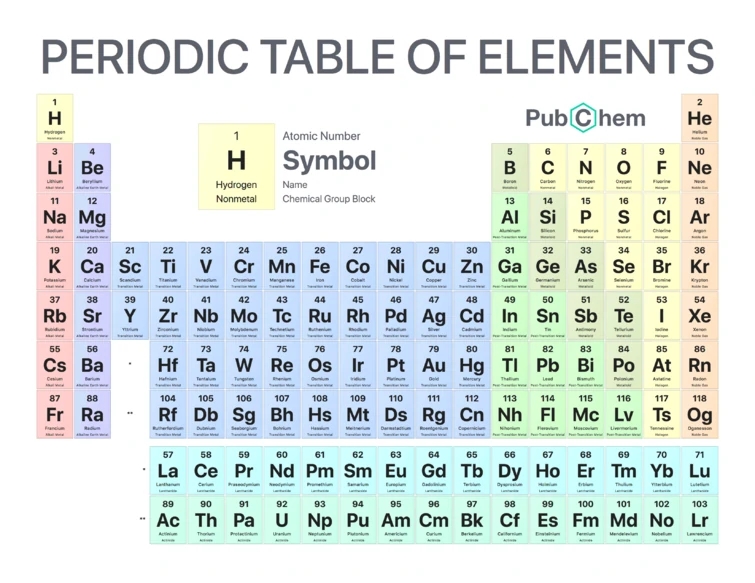
Here's another common kind of periodic table that I hate. It cuts a hole into the bottom two rows of the transition metals, and moves the metals that should be there — elements 71 and 103 — into the rare earths and actinides.
This amounts to claiming that there are 15 rare earths and actinides, and just 9 transition metals in those two rows. That’s crazy: the fact that the p subshell holds 10 electrons and the d subshell holds 14 is dictated by group representation theory. Subshells hold 2, 6, 10, 14 electrons — twice odd numbers.
The periodic table is a marvelous thing: it shows how quantum mechanics and math predict patterns in the elements. Subshells hold 2, 6, 10, 14 electrons — twice odd numbers. Have fun making up new designs — but if you're going to use the old kind, use the good one!
If you don't believe me, listen to this guy:
But unlike him, I don't think experiments were necessary to realize that the bad periodic tables were messed up. It's not as if they were designed based on some alternative theory about which elements would be transition metals.
Interestingly, the International Union of Pure and Applied Chemistry were
supposed to meet at the end of last year to settle this issue. What
did they decide? If you find out, please let me know!
January 15, 2022
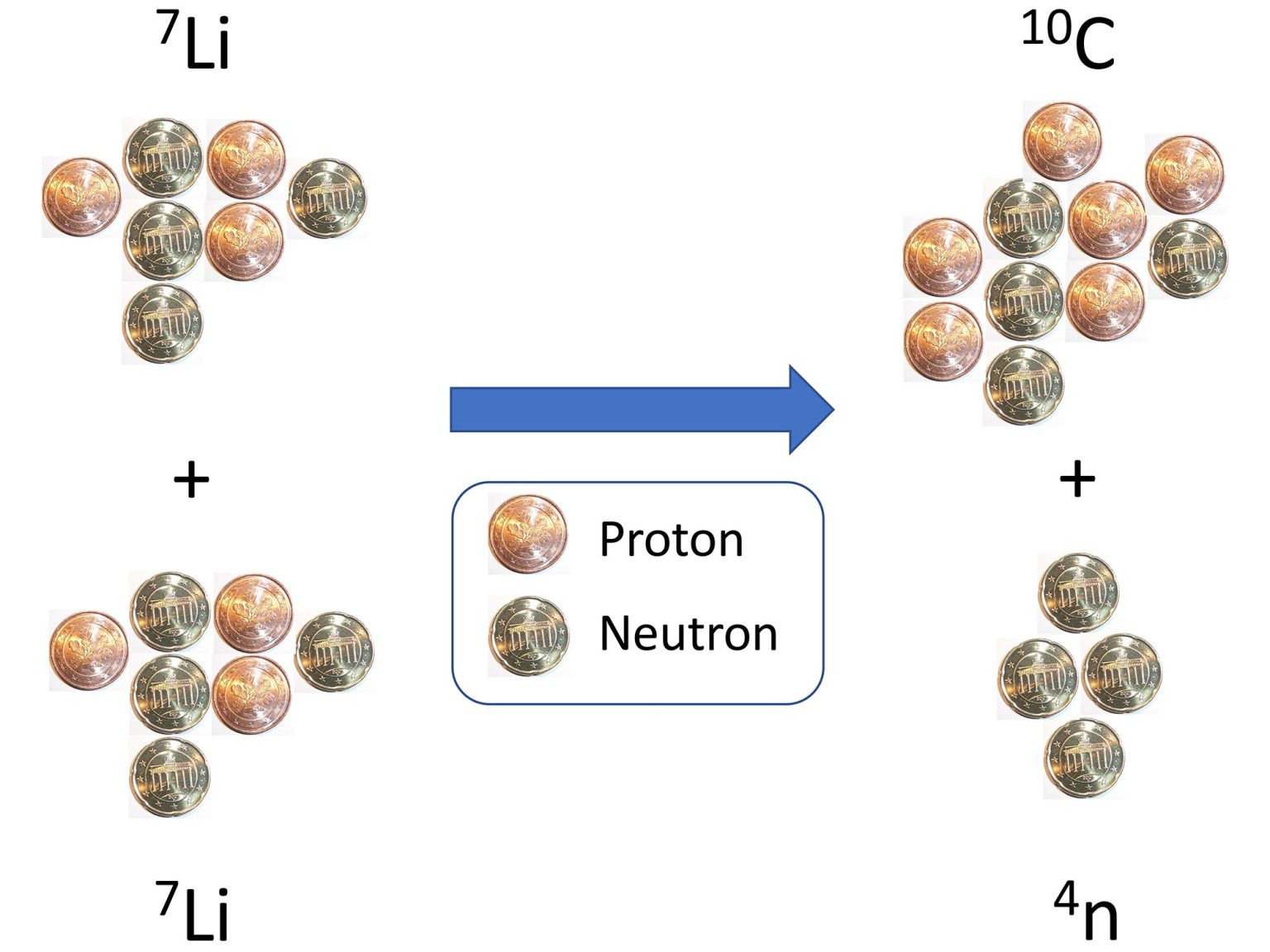
It's a bit surprising that 1 or even 2 protons stick to a neutron better than 2 neutrons stick to each other. The 'dineutron' is extremely unstable! So it's exciting that late last year, people made some 'tetraneutrons' by colliding nuclei of lithium-7.
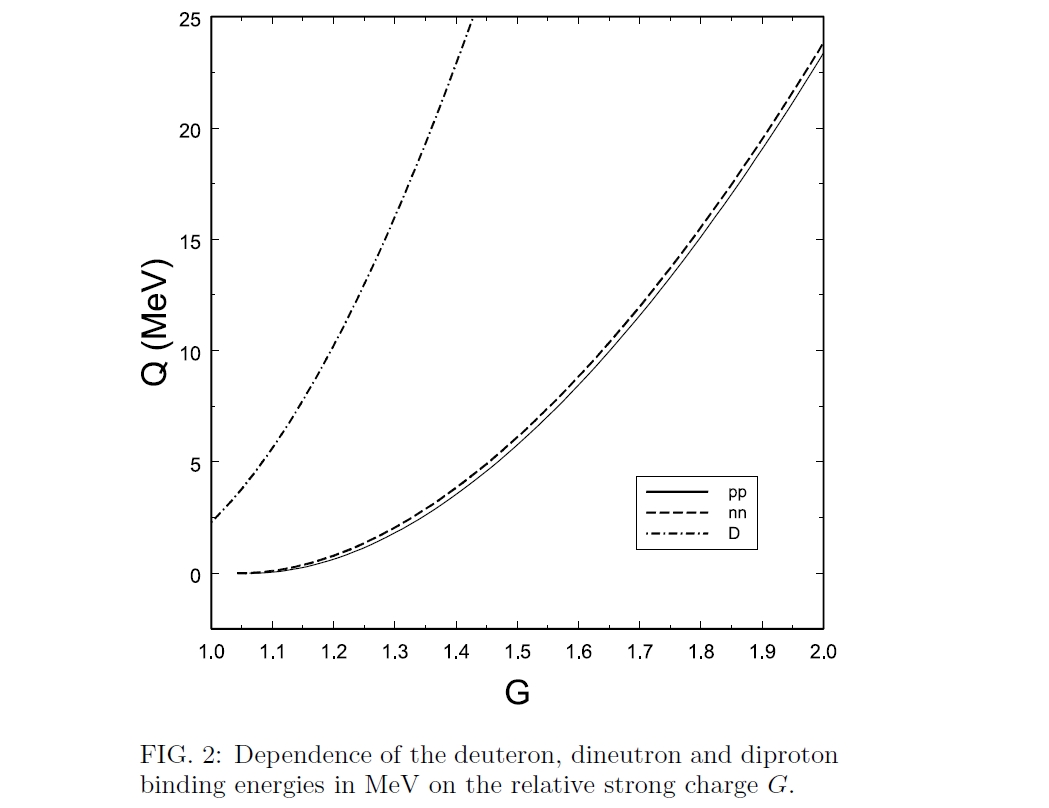
The dineutron (nn) is less stable than the deuteron (pn) since Pauli exclusion forbids two identical fermions from being in the same state. But if the strong force coupling constant G were just a bit bigger, the deuteron and even the diproton (pp) would be stable!
Some argue that with a slightly stronger strong force, all hydrogen would turn into dineutrons and diprotons in the early universe, killing off any chance for life. This paper argues otherwise: there would be less hydrogen left, but not none:
A subdwarf B star is a blue-hot star smaller than the Sun. A few of these crazy stars pulse in brightness as fast as every 90 seconds! Waves of ionizing iron pulse through their thin surface atmosphere.
What's up with these weird stars?
Sometimes a red giant loses most of its outer hydrogen... nobody is sure why... leaving just a thin layer of hydrogen over its helium core. We get a star with at most 1/4 the diameter of the Sun, but really hot.
It's the blue-hot heart of a red giant, stripped bare.
Iron and other metals in the star's thin hydrogen atmosphere can lose and regain their outer electrons. When these electrons are gone, the metals are 'ionized' and they absorb more light. This pushes them further out. Then they cool, become less ionized, absorb less light, and fall back down. This heats them up, so they become more ionized and the cycle begins again.
This happens in standing waves, which follow spherical harmonic patterns. You may have seen spherical harmonics in chemistry, where they describe electron orbitals. The same math is being applied here to a whole star! Now it's not the electron's wavefunction that's pulsing in a spherical harmonic: it's metals in the atmosphere of a star.
When the star is rotating, spherical harmonics that would otherwise vibrate at the same frequency do so at different frequencies. So, just by looking at the pulsing of light from a distant subdwarf B star, you can learn how fast it's rotating!
I got the gif of a pulsing star from here:
Pulsating white dwarf stars also oscillate in spherical harmonic patterns, and this website shows how they look.The figure showing frequency lines is from this cool paper:
This paper says "a κ-mechanism triggered by an accumulation of heavy elements (in particular iron) in the stellar envelope caused by radiative levitation is driving the oscillation."
So, what's the κ-mechanism and radiative levitation?
The κ-mechanism causes oscillations when a layer of a star's atmosphere gets more opaque at higher temperatures. For example, when heavy metals near the surface of the atmosphere get hot they can ionize, and thus absorb more radiation. When the layer of ions falls in it gets hotter, more opaque, blocks more escaping heat, and the star's pressure goes up... pushing the layer out. But when the layer shoots out it gets cooler, less opaque, blocks less escaping heat, and the pressure drops again. So we can get oscillations!
Radiative levitation can drive heavy metals to the surface of a star. They absorb light, and the light literally pushes them up. This can make these metals thousands of times more common than you'd expect near the surface.
There's more that can happen with subdwarf B stars, and you can learn about it here:

Why is mercury liquid at room temperature? It's connected to special relativity. Its innermost electrons are moving at about 58% the speed of light, so thanks to special relativity they become 23% heavier and their orbit about 23% smaller! Without special relativity, mercury would melt at about 80 °C.
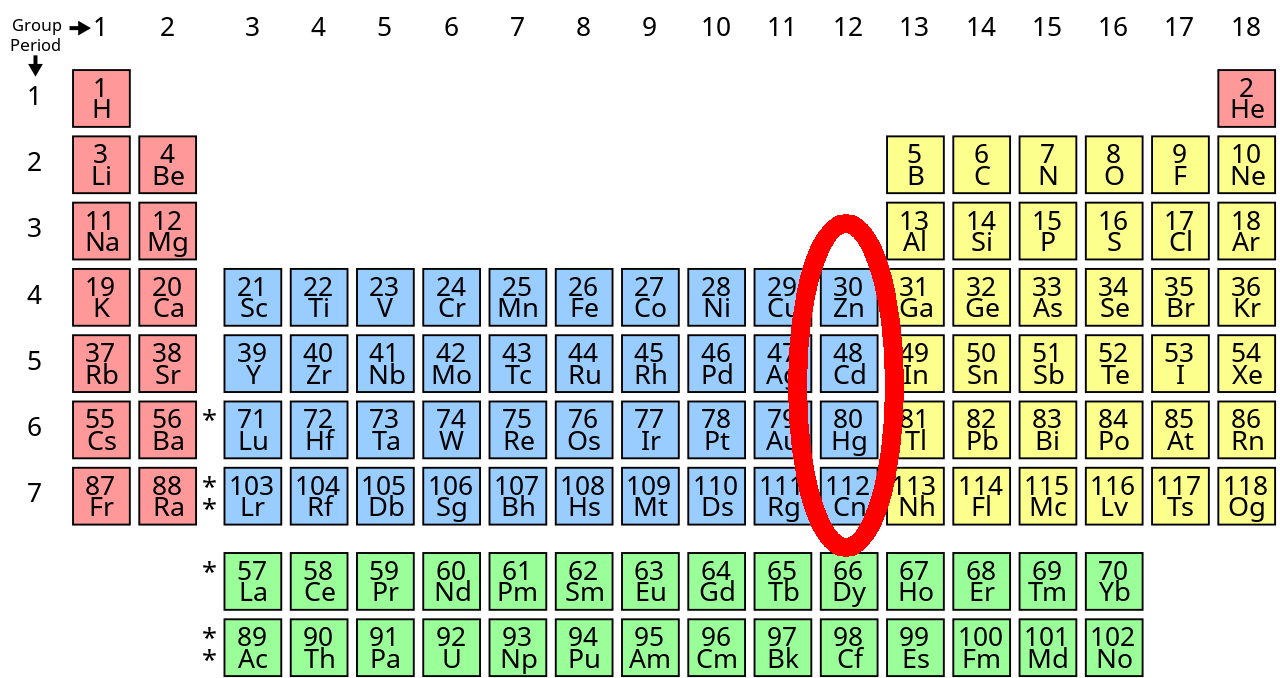
The transition metals on the far right, called group 12, are weird compared to the rest because the d subshell is completely full at this point. Zinc is hard, cadmium is soft and mercury is actually liquid. (Alas, all isotopes of copernicium, Cn, have half-lifes of less than 10 seconds.)
In mercury not only is the d subshell completely full, electrons in the inner shells are moving fast because the charge of the nucleus is so high. Special relativity makes those electrons heavier, and this means they orbit closer to the nucleus.
The filled outer d subshell and smaller inner subshells makes mercury especially non-reactive. So its atoms don't even like to stick to each other. So instead of forming a crystal at room temperature, mercury is liquid! For details, read this:
What really got me into this was trying to understand how group 12 transition metals are different, due to their completely filled d subshell. I still haven't learned enough about this!
Here's a nice place to learn more about group 12 elements:
Note: just two words! His translation into English was more verbose:
Tom Manzanec's more literal translation does a nice job of explaining the original to those of us who can't read classical Chinese — like, how you could write a poem with just two words!
Here's a bit more about Thich Nhat Hanh, which begins to explain why Martin Luther King nominated him for the Nobel Peace Prize. He didn't just sit around and meditate.
I found out about his poem from Tom Manzanec
on
Twitter.
January 25, 2022