

On the first day of the Russian invasion of Ukraine, Snake Island was attacked by the Russian Navy. When the Russian cruiser Moskva hailed the island's garrison over the radio demanding their surrender, a Ukrainian soldier replied "Russian warship, go fuck yourself". This incident was later commemorated in a Ukrainian stamp.
At the time of the incident, it was thought the Ukrainian soldiers were killed. But in fact they were captured — and later released in a prisoner exchange. The one who made the remark was later given a medal, and on April 13h the Ukrainians hit the Moskva with two anti-ship missiles, and it sank.

I spent a lot of March reading and tweeting about the Russian invasion
of Ukraine: it was a horrifying and all-consuming experience.
But I won't copy most of those tweets to my online diary,
since a lot of them were trying to guess forthcoming events, and
they're less interesting now. I think I did pretty well.
March 2, 2022

This is me preparing a talk on applied category theory. You may see the egg, but I see the bird.
On February 16th I gave a talk on "Categories: the Mathematics of Connection" at a workshop on the Mathematics of Collective Intelligence at UCLA, and you can see my slides and a video of my talk:


Walking around near Magnolia and 13th Street in Riverside, near the courthouse, I found a more depressing scene than the center of town, which is undergoing a kind of boom. Down here, a restaurant had burnt down! It's called Mr T.'s, and it was a popular spot for people who had business at the court. I first saw it during jury duty. It was closed around 2019 after a kitchen fire, but in January of this year it completely burnt down. An arson investigator said the fire was not intentionally set, but the exact cause was listed as undetermined.
A block further north, at 3700 12th street, the restaurant Lisa and used to go to a lot — the Salted Pig — is gone, having moved to a nice location near the center of town. Luckily it seems to be getting replaced by the Roots Restaurant and Bar, which is still in the process of applying for its liquor license.
Unfornately, the nice little coffee house next door, Auggies, is closed and emptied out. I guess it's not coming back — probably another victim of the coronavirus pandemic. The bar a bit south of there on 4281 Main Street, called W. Wolfskill, is "temporarily closed".
Further north, at 3796 10th Street, I saw an emptied-out building with a note on the door. Walking up, I saw the note said "This tenant did not pay their rent for 6 months. Despite the availability of COVID assistance and taking advantage of this assistance, they did not pay their rent for 6 months."

Psychologist when your country is being invaded:


It's easy to remember when Pi Day happens, because it's also Einstein's birthday.
Proved matter is made of atoms. Discovered light comes in particles.
Unified space and time. Discovered E = mc2. Discovered
energy bends spacetime, and that's gravity. Dreamt up the cosmological
constant, wormholes and quantum entanglement, and more.
March 23, 2022
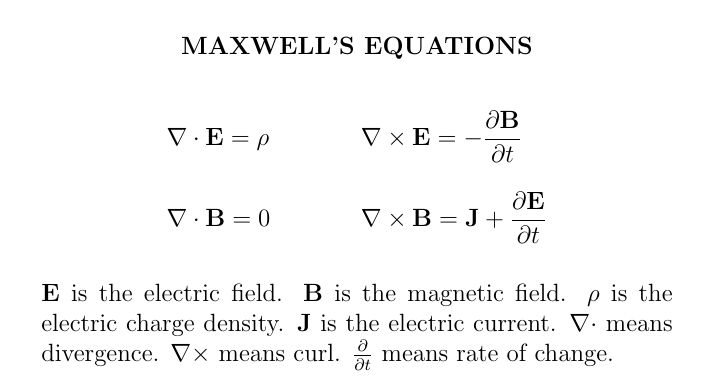
Four equations tell us everything we need to know about the electric and magnetic field — not counting the the behavior of the matter that they interact with, or the subtleties of quantum mechanics.
This is when I started really loving physics.
Using special relativity we can reduce these four equations to two, since it unifies the electric and magnetic field, and it unifies electric charge density and current. Using gauge theory we can reduce these two equations to just one!
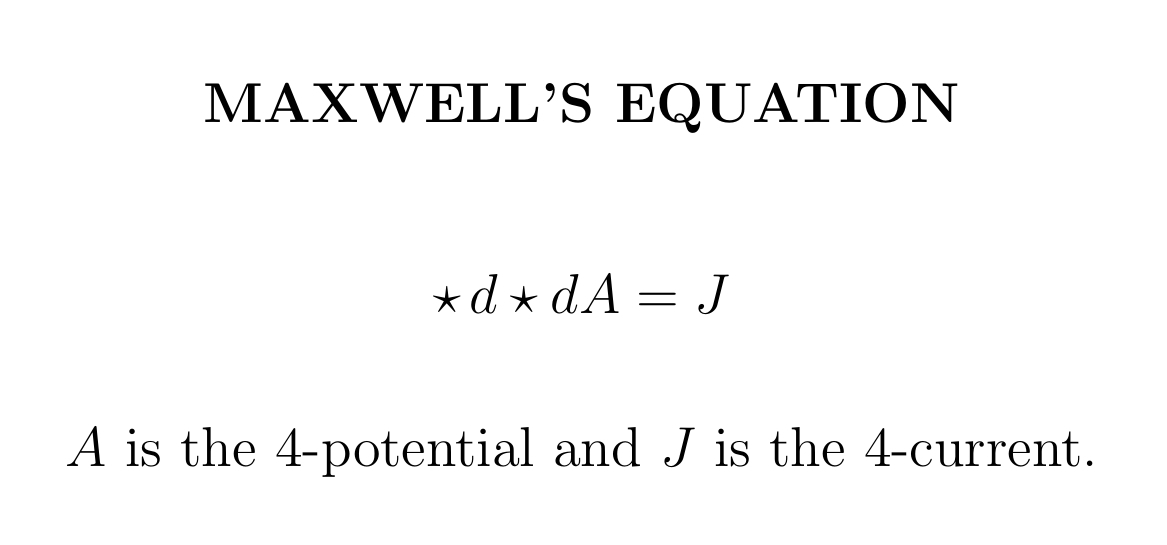
In the days to come I'll explain Maxwell's four equations separately. I'll keep the explanations simple and sketchy: I won't go far into the math. If you want more detail, try the Feynman lectures:
By the way, I'm using a version of Maxwell's equations where some physical constants have been set to 1 by a clever choice of units of measurement. For practical work you may want to keep these constants visible. There are several common ways of doing this.
I call this the first Maxwell equation since it was discovered first:

Fossilized tree sap, called amber, picks up a positive electric charge when you rub it with wool. Then you can detect the electric field diverging from it! The ancient Greeks called amber 'ēlektron' — and thanks to this substance, we learned about the electric field.

In the 1700s people became fascinated by the electric field, and started developing the math needed to understand it. What I'm calling the first Maxwell equation was first formulated by Legendre in 1773, and then clarified by Gauss:
The total amount of electric charge in any region equals the flux of electric field through the boundary of that region.This is equivalent to saying \(\nabla \cdot \mathbf{E} = \rho\) at every point!
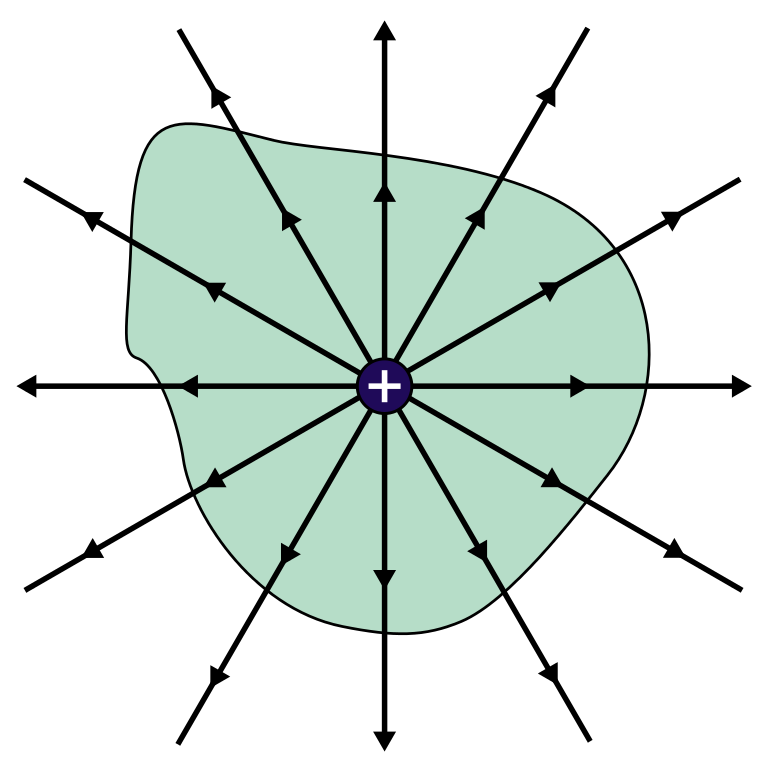
It's not obvious that these two formulations of the Gauss law are equivalent! This fact is called the 'divergence theorem', and it was proved by Ostrogradsky in 1826:
So amber helped spark a revolution! For the full story, try Crowe's
A History
of Vector Analysis and Whittaker's
A History of the Theories of Aether and Electricity.
March 24, 2022
Like the electric field, the magnetic field \(\mathbf{B}\) is an arrow
at each point of space. But the second Maxwell equation says that
unlike the electric field, the magnetic field can never point outwards
or inwards from some point. Its divergence is zero!

Just as fascination with the electric field started with a strange rock called ēlektron by the Greeks, the magnetic field was discovered thanks to a strange rock now called magnetite — because it was found near the city of Magnesia. It attracts iron!

Now we can make magnets, and see the magnetic field using iron filings. It may seem that this field diverges at one end of a magnet and converges at the other, but this is an illusion. If you chop a magnet in half you never get just a north pole or just a south pole!
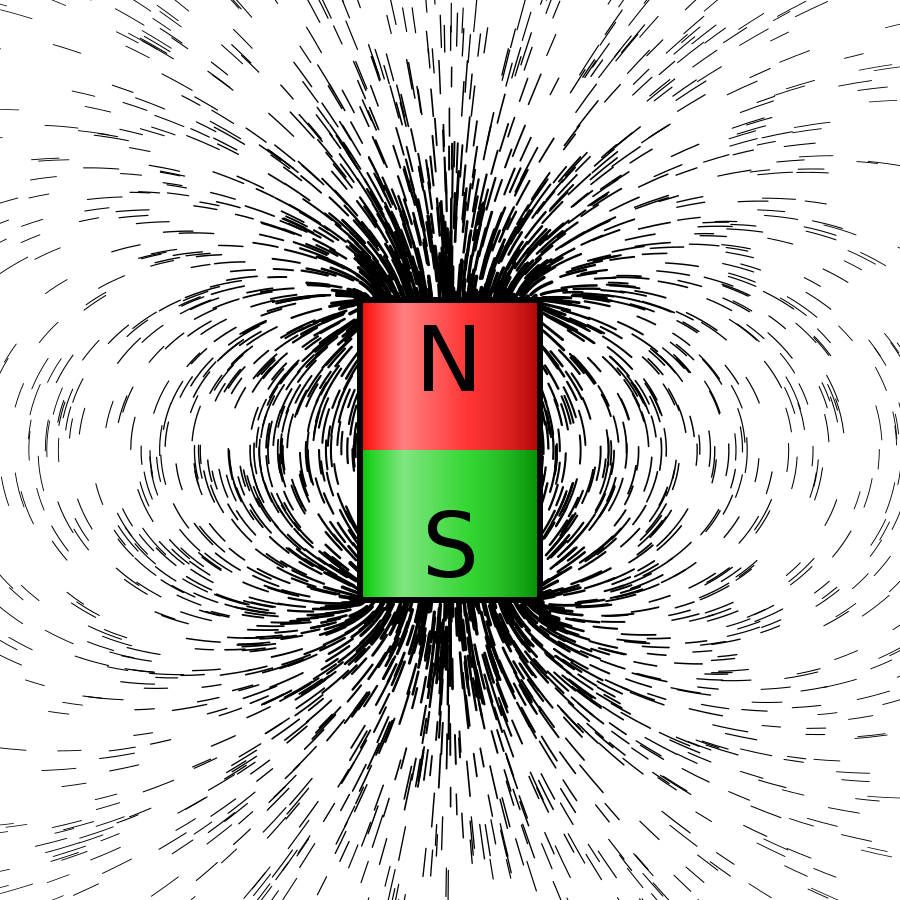
Despite intensive searches, physicists have never found a place where the magnetic field diverges or converges. Instead, the magnetic field near a tiny magnetized piece of iron looks like this:
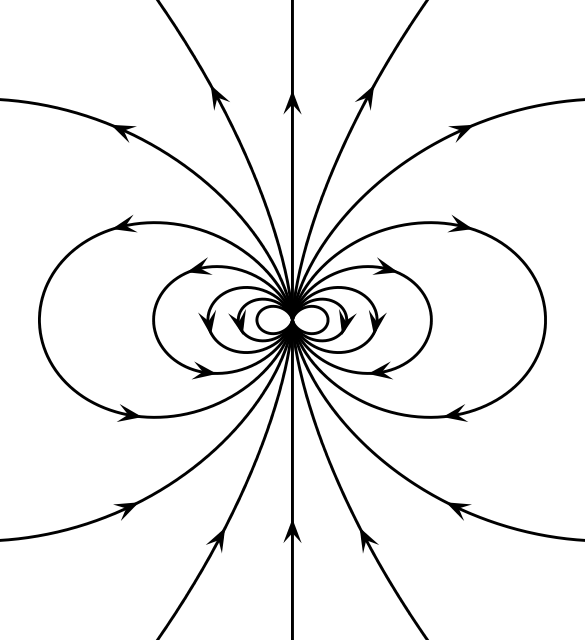
Its divergence is zero!
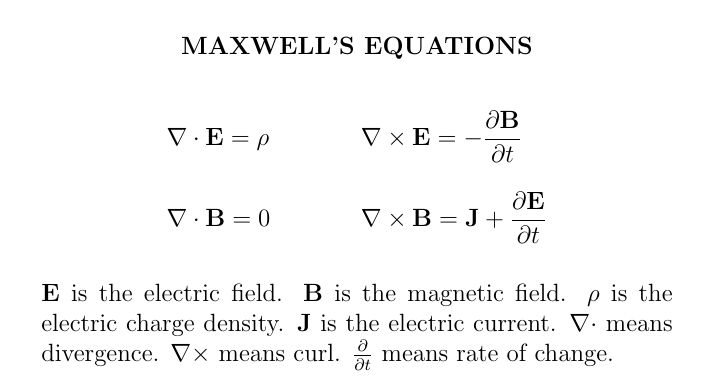
The first two Maxwell equations are about the divergence of the electric and magnetic fields at any moment in time.
The other two say how these fields change with time. This depends on how they curl around!
I'll begin explaining this tomorrow.
March 25, 2022
A changing magnetic field makes the electric field curl around. So if
you move a magnet through a loop of wire, the electric field will push
electrons around the wire — and you'll get an electric current!
The third Maxwell equation makes this precise.

This effect was discovered by Faraday in 1831, using an experiment roughly like this:
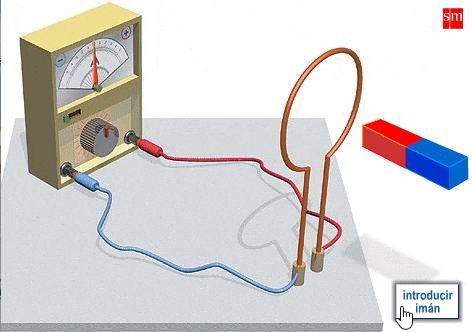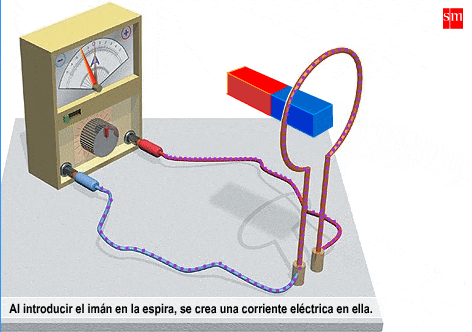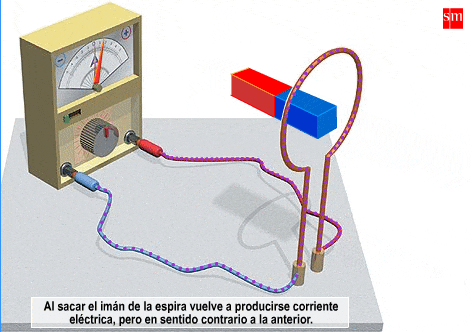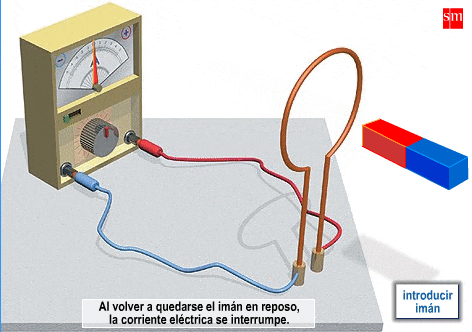
So one version of Maxwell's third equation is also called 'Faraday's law of induction'.
Maxwell described the mathematical concept of 'curl' 40 years later, in 1871.
Faraday's actual experiment looked like this:
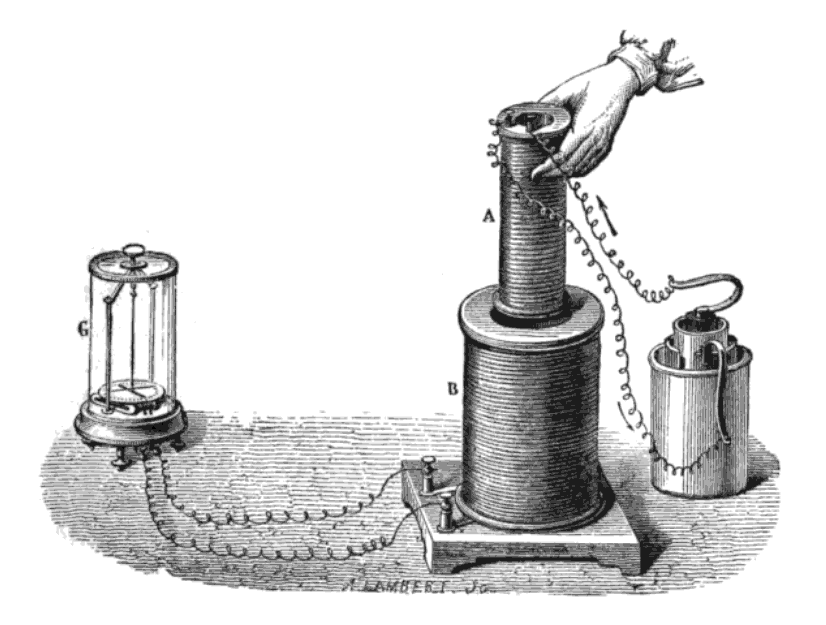
He didn't use a bar magnet. He used an electromagnet powered by a battery: the way electric current makes a magnetic field is described by Maxwell's fourth equation! And he moved this magnet through a big coil of wire, B.
Here is Maxwell's 1871 paper where he split the derivative of a vector field into two parts: the convergence, whose negative we now call the divergence, and the curl:
It's fun to see him trying out different names for the curl!
To really understand Maxwell's equations, you need to understand divergence and curl. There are formulas for these, which I'm deliberately not mentioning! Before studying these formulas, it's good to get some more intuition using pictures:
You can also read more about Faraday's law of induction!
Faraday described \(\mathbf{E}\) and \(\mathbf{B}\) as 'lines of
force'. Since he didn't formulate his ideas using math, most
physicists rejected them — except Maxwell... who formulated them using
math.
March 26, 2022
The physicist Ørsted discovered that electric current makes the magnetic field curl around it.
Maxwell realized that a changing electric field does this too.
Maxwell's fourth equation says exactly how this works. This completes the theory of electromagnetism!

Electric current makes the magnetic field curl around it. This is called 'Ampère's circuital law'. As I can tell, it was discovered earlier by Ørsted. But the history of physics is always complex.

More importantly, this is how electromagnets work! You can make an electromagnet yourself, like this:

The current flowing through the coiled wire makes a magnetic field which points along the direction of the nail. The iron in the nail then becomes magnetized — a more complicated phenomenon.
In 1855, Maxwell realized that a changing electric field also makes the magnetic field curl around!
In fact, without this extra effect, Ampère's circuital law contradicts the conservation of electric charge in any situation where the electric charge density changes:
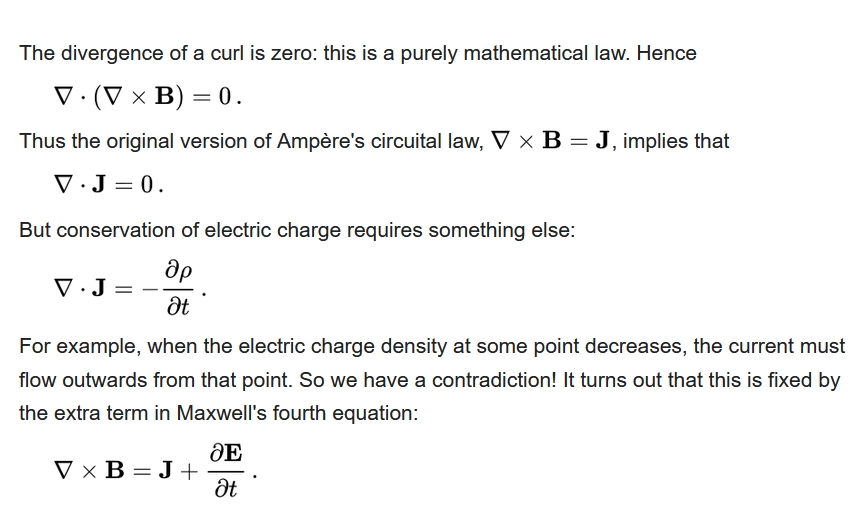
With this extra term, a curling \(\mathbf{B}\) field makes the \(\mathbf{E}\) field change, and a curling \(\mathbf{E}\) field makes the \(\mathbf{B}\) field change.
So, electric and magnetic fields can form waves in the vacuum.
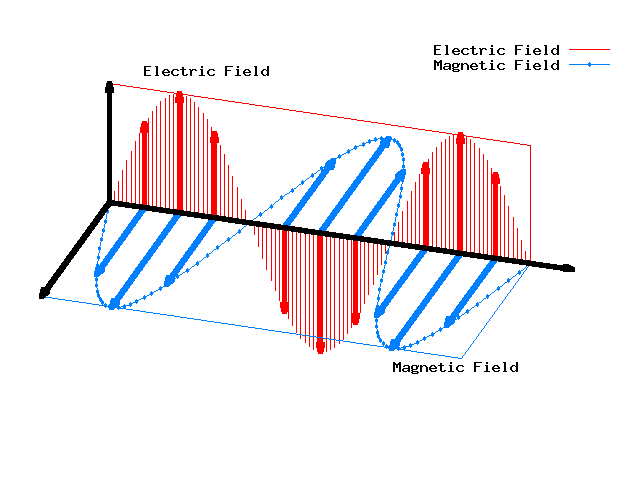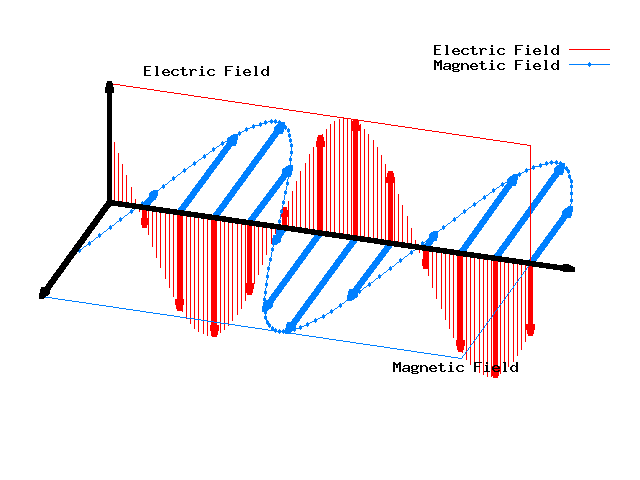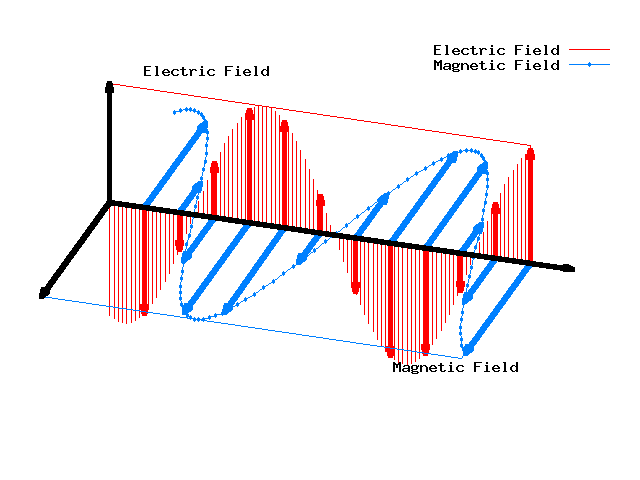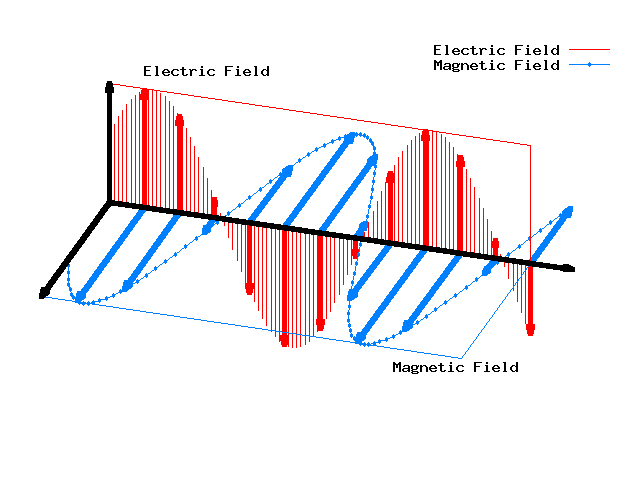

To get the right speed of light we need to include the constants in Maxwell's equations that I've been setting equal to 1 by a clever choice of units. See the T-shirt for these constants.

In November 1886, Hertz tested this idea by using an electric spark to create radio waves! The full story is here:

Maxwell's originally listed 20 equations, not using modern vector equation. Heaviside brought them down to today's four in his book Electromagnetic Theory, whose first volume was published in 1893.
For more on this, read:

Modern civilization would be impossible without Maxwell's equations.
My laptop is communicating to you with the help of Hertz's waves. And
its circuits and display use an intricate blend of electromagnetism
and quantum mechanics. It's amazing!
March 28, 2022
Electric charge is conserved. But it's not just that the total charge
of the whole universe stays the same — a rather useless statement.
It's that charge can't leave one location without going somewhere else
nearby!
We can write an equation that says this.

Even better, conservation of charge follows automatically from two of Maxwell's equations.
If the current diverges, it causes a decrease in the divergence of the electric field, which is only possible if the charge density decreases!
It's fun to really visualize this.

Please try to visualize each step here.
As current shoots outward, it must produce an electromagnetic field. It can make a curling \(\mathbf{B}\) field, but it must make a changing \(\mathbf{E}\) field — whose decreasing divergence is only explicable by a decrease in charge density!
I fell in love with mathematical physics when I saw this: it was the first time I'd seen field equations used to prove a conservation law. But only this week did I try to visualize what's going on!
This conservation law has a funny name:
These simpler equations describe how waves of light move through empty space.

The minus sign in the vacuum Maxwell equations looks funny. But it's okay! If we have any solution of these equations, we get another solution by replacing the electric field \(\mathbf{E}\) with the magnetic field \(\mathbf{B}\), and \(\mathbf{B}\) with \(-\mathbf{E}\).
This is called 'electromagnetic duality'.

If you take a complex number \(x+iy\) and multiply it by \(-i\), you get \(y-ix\). You're replacing \(x\) with \(y\) and \(y\) with \(-x\). So electromagnetic duality becomes multiplication by \(-i\) if you combine the electric and magnetic fields using the complex numbers:

Working with a complex electromagnetic field is quite practical.
You get half as many equations, with beautiful wave solutions like this. You can take the real part of a solution to get \(\mathbf{E}\) and the imaginary part to get \(\mathbf{B}\).
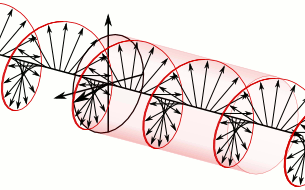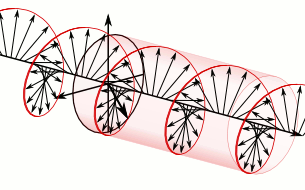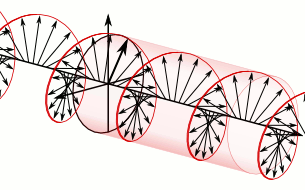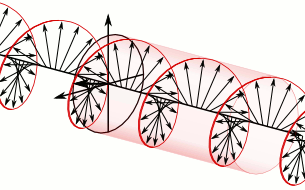
The complex electromagnetic field is sometimes called the Riemann–Silberstein vector. Apparently it first appeared in a lecture by Bernhard Riemann, published in 1901.

Above is an image from Riemann's published lecture, taken from here: