For my May 2008 diary, go here.

Diary - June 2008

John Baez

Today it's Sunday; I went to a cafe called Panera at the Riverside Plaza and spent several hours polishing up a draft of a paper I'm writing with my students Chris Rogers and Alex Hoffnung, called Categorified Symplectic Geometry and Classical String Theory.

I need to finish off a number of papers and prepare a few talks before I go to Barcelona on the 14th. I can get nervous if I think about how much I'm committed to do. And I still haven't found a place to stay for our stay in Paris starting July 6th! But I'll muddle through.

I read an article about some charmingly persistent scientists seeking radio broadcasts from extraterrestrial life — especially Rick Forster, who is working on an array 42 new radio dishes devoted to this search up in Hat Creek, a valley near Mt. Shasta in northern California:

• John Johnson Jr., Aliens get a new switchboard: a SETI radio telescope in Northern California, Los Angeles Times, June 1, 2008.

Frank Drake made his first attempt to find Earth's sister planet in 1960, using an 85-foot-diameter antenna at the National Radio Astronomy Observatory in West Virginia. Radio waves have long been considered ideal for communication with alien civilizations because the waves are easy to produce and receive, which is why we use them on Earth to carry television and radio signals. They also penetrate the gas and dust between stars.

Drake pointed the antenna at two nearby stars, Epsilon Eridani and Tau Ceti — virtually next-door neighbors in galactic terms at just over 10 light-years from Earth.

In April 1960, Drake picked up a signal. His first thought, according to Seth Shostak, was: "Can it be this easy?"

The second was, "Holy cow, what do I do now?"

"It wasn't that easy," said Shostak, who is writing a book about the search for alien intelligence.

Drake, now 78, had mistaken a passing aircraft for an alien broadcast. It was the first of many false alarms to haunt the field, presenting a problem that persists today: separating the man-made and natural radio signals from the electronic "Howdy, neighbor" of an alien civilization.

Shostak calls it the "E.T. or AT&T?" problem.

So how does one go about tuning in intergalactic radio? It's a lot more complicated than simply pointing your antenna at the right star, just as tuning in your favorite radio station on Earth requires more than being within broadcast range. You have to spin the dial.

The radio spectrum ranges over frequencies of 3 kilohertz (3,000 hertz) to 300 gigahertz (300 billion hertz). The alien version of "I Love Lucy" could be hiding anywhere in between.

With the Hat Creek array, SETI will be able to scan a much broader range than ever before: everything from 0.5 gigahertz to 11 gigahertz, a range of 10 billion channels.

When researchers get a promising signal, the real work begins.

The key test, according to Tarter, is the bandwidth. Nothing in nature produces signals narrower than 300 hertz.

"Quasars, pulsars, things like that make signals much broader," Shostak said. "A narrow signal must have been produced by a transmitter."

But whose? Ours or theirs?

The next step after finding a signal is to watch it for a while. Does it change, or does it sit there on the dial giving off a continuous whine or beeping as regularly as a metronome? An alien signal would undergo subtle changes as Earth's orbital position changed relative to the other planet, whereas a man-made signal would be constant.

"Getting a signal is not such a big deal," Shostak said. "At Arecibo, we got one every six seconds."

With the Hat Creek array, he expects to get a promising signal every couple of hours. Every six months, he expects, researchers will get one that seems to pass all the tests. But that's just the beginning. After that, SETI will alert other observatories for confirmation.

Over nearly 40 years of searching, no signal has panned out to be anything more than a satellite transmission or some mundane natural pulse.

But the time period is deceptive. All the actual search time added together amounts to only 18 months of concerted effort, Shostak said — hardly enough to conclude that our galactic brethren either are not there or are not interested in communicating.

For the truly dedicated, patience is not only a virtue but a requirement. Just ask Jill Tarter.

She began her search in the late 1970s at NASA's Ames Research Center in the Bay Area, where scientists were interested in following up on Drake's work.

Tarter signed on. "I realized I was alive in the first generation of human beings who could answer the are-we-alone question rather than going around asking priests and philosophers," she said. "Good grief, why wouldn't I want to become involved in that?"

The NASA search was killed by Congress in 1993, but Tarter refused to give up.

Maybe science requires a certain quixoticism: you're trying to do amazing, wonderful things, and most attempts fail — but overall science succeeds in doing amazing, wonderful things.

On another note: I recently read somewhere that Arecibo-quality radio antennas on other solar systems could only pick up the carrier wave of TV broadcasts from Earth like the I Love Lucy show mentioned above — not the actual signal.

But the big question is: is anyone out there? I last talked about the so-called Fermi paradox in my December 14, 2006 diary entry. It's not really a paradox, more like a puzzle. Here's a new article on the subject:

• Nick Bostrom, Where Are They? — Why I Hope The Search for Extraterrestrial Life Finds Nothing, Technology Review, May-June 2008.

I hope that our Mars probes discover nothing. It would be good news if we find Mars to be sterile. Dead rocks and lifeless sands would lift my spirit.

Conversely, if we discovered traces of some simple, extinct life-form — some bacteria, some algae — it would be bad news. If we found fossils of something more advanced, perhaps something that looked like the remnants of a trilobite or even the skeleton of a small mammal, it would be very bad news. The more complex the life-form we found, the more depressing the news would be. I would find it interesting, certainly — but a bad omen for the future of the human race.

So where is the Great Filter? Behind us, or not behind us?

If the Great Filter is ahead of us, we have still to confront it. If it is true that almost all intelligent species go extinct before they master the technology for space colonization, then we must expect that our own species will, too, since we have no reason to think that we will be any luckier than other species. If the Great Filter is ahead of us, we must relinquish all hope of ever colonizing the galaxy, and we must fear that our adventure will end soon — or, at any rate, prematurely. Therefore, we had better hope that the Great Filter is behind us.

What has all this got to do with finding life on Mars? Consider the implications of discovering that life had evolved independently on Mars (or some other planet in our solar system). That discovery would suggest that the emergence of life is not very improbable. If it happened independently twice here in our own backyard, it must surely have happened millions of times across the galaxy. This would mean that the Great Filter is less likely to be confronted during the early life of planets and therefore, for us, more likely still to come.

If we discovered some very simple life-forms on Mars, in its soil or under the ice at the polar caps, it would show that the Great Filter must come somewhere after that period in evolution. This would be disturbing, but we might still hope that the Great Filter was located in our past. If we discovered a more advanced life-form, such as some kind of multicellular organism, that would eliminate a much larger set of evolutionary transitions from consideration as the Great Filter. The effect would be to shift the probability more strongly against the hypothesis that the Great Filter is behind us. And if we discovered the fossils of some very complex life-form, such as a vertebrate-like creature, we would have to conclude that this hypothesis is very improbable indeed. It would be by far the worst news ever printed.

For example, it would be really scary finding remnants of a dead civilization in the midst of an endless series of primary elections between two candidates in the same political party, either one of whom could have saved the day.

June 2, 2008

I've been studying Pythagoreanism ever since giving the first trial runs of my talk on the number 5, which features the so-called Pythagorean pentagram. The idea behind that pentagram was almost completely without historical basis, just a nice mathematical "just so story". But, it can't hurt to learn the history.

And, despite a profusion of legends in the later Greek literature, it turns out almost nothing is known of Pythagoras himself — and very little about the Pythagoreans of the 5th century BC. Tim Silverman. recommended this book:

• Walter Burkert, Lore and Science in Ancient Pythagoreanism, Harvard U. Press, Cambridge, Massachusetts, 1972.

No other branch of history offers such temptations to conjectural reconstruction as does the history of mathematics. In mathematics, every detail has its fixed and unalterable place in a nexus of relations, so that it is often possible, on the basis of a brief and casual remark, to reconstruct a complicated theory. It is not surprising, then, that gap in the history of mathematics that was opened up by a critical study of the evidence about Pythagoras has been filled by a whole succession of conjectural supplements.

• S. K. Heninger, Jr., Touches of Sweet Harmony: Pythagorean Cosmology and Renaissance Poetics, The Huntington Library, San Marino, California, 1974.

To get the importance of the tetractys, you have to temporarily throw out modern scientific thinking and get yourself in the mood of magical thinking, or correlative cosmology. To the Pythagoreans, the four rows of the tetractys represent the point, line, triangle and tetrahedron, respectively. The "fourness" of the tetractys also represents the four elements: earth, air, water and fire. I'm not sure if there are specific elements that correspond to the numbers 1, 2, 3, and 4, though. The Renaissance thinkers liked to organize the elements using the chain of analogies

(running from light to heavy), or in a pattern like this:

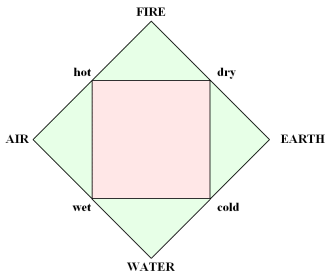
Fire is primarily hot and secondarily dry.
Air is primarily wet and secondarily hot.
Water is primarily cold and secondarily wet,
Earth is primarily dry and secondarily cold.

The tetractys also took the Pythagoreans in other strange directions. For example, who said this:

A modern-day string theorist, talking to a loop quantum gravity theorist about the dimension of spacetime? No! Lucian attributes it to Pythagoras, referring to the tetratkys and the fact that 1 + 2 + 3 + 4 = 10. This somehow led the Pythagoreans to consider the number 10 as representing perfection.

Pythagorean music theory is a bit more comprehensible. The Greeks, and the Babylonians before them, knew that nice-sounding intervals in music correspond to nice rational numbers. For example, they knew that the octave corresponds to a ratio of 2:1. We'd now call this a ratio of frequencies; one can get into some interesting scholarly arguments about when and how well the Greeks knew that sound was a vibration, but never mind — read Burkert's book if you're interested in that question.

Whatever these ratios meant, they also knew that the fifth corresponded to a ratio of 3:2, and a fourth to 4:3.

They then figured out that the octave could be divided into a fourth and a fifth:

2/1 = 4/3 × 3/2

and at some point they defined a whole tone to be the difference, or really ratio, between a fifth and a fourth:

(3/2)/(4/3) = 9/8

So, when you go up one whole tone in Pythagorean tuning, the higher note should vibrate 9/8 as fast as the lower one. If you try this on a modern keyboard, it looks like after going up 6 whole tones you've gone up an octave. But in fact if you buy the Pythagorean definition of whole tone, 6 whole tones equals

(9/8)⁶ = 531441 / 262144 ≅ 2.027286530...

which is, umm, not quite 2. Another way to put it is that if you go up 12 fifths, you've almost gone up 7 octaves, but not quite: the so-called circle of fifths doesn't quite close, since

(3/2)¹²/2⁷ = 531441/524288 ≅ 1.01264326...

This annoying little discrepancy is called the Pythagorean comma.

Unfortunately, this sort of discrepancy is an unavoidable fact of mathematics. Our ear likes to hear frequency ratios that are nice simple rational numbers, and we'd also like a scale where the notes are evenly spaced, but we can't have both. Why? Because you can't divide an octave into equal parts that are rational ratios of frequencies: a nontrivial nth root of 2 can never be rational.

So, irrational numbers are lurking in any attempt to create an equally spaced (or as they say, "equal-tempered") tuning system. And you might imagine this pushed the Pythagoreans to confront irrational numbers. This case has been made by the classicist Tannery, but Burkert doesn't believe it: there's no written evidence suggesting it.

You could say the existence of irrational numbers is the root of all evil in music. Indeed, the diminished fifth in an equal tempered scale is called the diabolus in music, the "devil in music", and it has a frequency ratio of √2.

Or, you could say that this built-in conflict is the spice of life! It makes it impossible for harmony to be perfect and therefore dull.

Anyway, Pythagorean tuning is not equal-tempered: it's based on making lots of fifths equal to exactly 3/2. So, all the frequency ratios are fractions built from the numbers 2 and 3. But, some of them are nicer than others:

first = 1/1
second = 9/8
third = 81/64
fourth = 4/3
fifth = 3/2
sixth = 27/16
seventh = 243/128
octave = 2/1

As you can see, the third, sixth and seventh are not very nice: they're complicated fractions so they don't sound great. They're all a bit sharp compared to the following tuning system, which is a form of "just intonation":

first = 1/1
second = 9/8
third = 5/4
fourth = 4/3
fifth = 3/2
sixth = 5/3
seventh = 15/8
octave = 2/1

A long and interesting tale could be told about this other system, but I won't tell it here. Instead, let's just study how the third, sixth and seventh differ:

• In just intonation the third is 5/4 = 1.25, but in Pythagorean tuning it's 81/64 = 1.265625.
• In just intonation the sixth is 5/3 = 1.6666.., but in Pythagorean tuning it's 81/64 = 1.6875.
• In just intonation the seventh is 15/8 = 1.875, but in Pythagorean tuning it's 243/128 = 1.8984375.

For more information on Pythagorean tuning, try the Wikipedia article. For now, I just want to say how it's related to other aspects of Pythagorean or Platonic numerology, especially the so-called "Platonic Λ".

The "Platonic Λ" is a certain way of labelling the edges of the tetractys by powers of 2 on one side, and powers of 3 on the other:

           1

        2     3
       
     4           9

  8                 27

            1

        2      3
      
     4      6     9

  8    12     18     27

In this plate, the elements fire, air, water and earth are labelled by the numbers 8, 12, 18 and 27. This makes the aforementioned analogies:

into strict mathematical proportions:

In my effort to get to the bottom of this, I was soon led to a bizarre passage in Plato's Timaeus — a passage I'd never before come close to understanding! It describes the Platonic Λ and further ideas which seem closely related to Pythagorean tuning and perhaps the "music of the spheres".

Before I show you this passage, which is quite dense and bewildering, let me quote the introduction to the Timaeus written by Jowett, one of the main translators of Plato into English. First, some general stuff about the role of number in Greek thought:

Number and figure were the greatest instruments of thought which were possessed by the Greek philosopher; having the same power over the mind which was exerted by abstract ideas, they were also capable of practical application. Many curious and, to the early thinker, mysterious properties of them came to light when they were compared with one another. They admitted of infinite multiplication and construction; in Pythagorean triangles or in proportions of 1:2:4:8 and 1:3:9:27, or compounds of them, the laws of the world seemed to be more than half revealed. They were also capable of infinite subdivision — a wonder and also a puzzle to the ancient thinker (Republic). They were not, like being or essence, mere vacant abstractions, but admitted of progress and growth, while at the same time they confirmed a higher sentiment of the mind, that there was order in the universe. And so there began to be a real sympathy between the world within and the world without. The numbers and figures which were present to the mind's eye became visible to the eye of sense; the truth of nature was mathematics; the other properties of objects seemed to reappear only in the light of number. Law and morality also found a natural expression in number and figure. Instruments of such power and elasticity could not fail to be 'a most gracious assistance' to the first efforts of human intelligence.

The proportions in which the soul of the world as well as the human soul is divided answer to a series of numbers 1, 2, 3, 4, 9, 8, 27, composed of the two Pythagorean progressions 1, 2, 4, 8 and 1, 3, 9, 27, of which the number 1 represents a point, 2 and 3 lines, 4 and 8, 9 and 27 the squares and cubes respectively of 2 and 3. This series, of which the intervals are afterwards filled up, probably represents (1) the diatonic scale according to the Pythagoreans and Plato; (2) the order and distances of the heavenly bodies; and (3) may possibly contain an allusion to the music of the spheres, which is referred to in the myth at the end of the Republic.

Now God did not make the soul after the body, although we are speaking of them in this order; for having brought them together he would never have allowed that the elder should be ruled by the younger; but this is a random manner of speaking which we have, because somehow we ourselves too are very much under the dominion of chance. Whereas he made the soul in origin and excellence prior to and older than the body, to be the ruler and mistress, of whom the body was to be the subject. And he made her out of the following elements and on this wise: Out of the indivisible and unchangeable, and also out of that which is divisible and has to do with material bodies, he compounded a third and intermediate kind of essence, partaking of the nature of the same and of the other, and this compound he placed accordingly in a mean between the indivisible, and the divisible and material. He took the three elements of the same, the other, and the essence, and mingled them into one form, compressing by force the reluctant and unsociable nature of the other into the same. When he had mingled them with the essence and out of three made one, he again divided this whole into as many portions as was fitting, each portion being a compound of the same, the other, and the essence. And he proceeded to divide after this manner:

First of all, he took away one part of the whole (1), and then he separated a second part which was double the first (2), and then he took away a third part which was half as much again as the second and three times as much as the first (3), and then he took a fourth part which was twice as much as the second (4), and a fifth part which was three times the third (9), and a sixth part which was eight times the first (8), and a seventh part which was twenty-seven times the first (27). After this he filled up the double intervals (i.e. between 1, 2, 4, 8) and the triple (i.e. between 1, 3, 9, 27) cutting off yet other portions from the mixture and placing them in the intervals, so that in each interval there were two kinds of means, the one exceeding and exceeded by equal parts of its extremes (as for example 1, 4/3, 2, in which the mean 4/3 is one-third of 1 more than 1, and one-third of 2 less than 2), the other being that kind of mean which exceeds and is exceeded by an equal number, e.g:

- over 1, 4/3, 3/2, - over 2, 8/3, 3, - over 4, 16/3, 6, - over 8: and
- over 1, 3/2, 2, - over 3, 9/2, 6, - over 9, 27/2, 18, - over 27.

Where there were intervals of 3/2 and of 4/3 and of 9/8, made by the connecting terms in the former intervals, he filled up all the intervals of 4/3 with the interval of 9/8, leaving a fraction over; and the interval which this fraction expressed was in the ratio of 256 to 243, e.g.

243:256::81/64:4/3::243/128:2::81/32:8/3::243/64:4::81/16:16/3::242/32:8.

And thus the whole mixture out of which he cut these portions was all exhausted by him. This entire compound he divided lengthways into two parts, which he joined to one another at the centre like the letter X, and bent them into a circular form, connecting them with themselves and each other at the point opposite to their original meeting-point; and, comprehending them in a uniform revolution upon the same axis, he made the one the outer and the other the inner circle. Now the motion of the outer circle he called the motion of the same, and the motion of the inner circle the motion of the other or diverse. The motion of the same he carried round by the side (i.e. of the rectangular figure supposed to be inscribed in the circle of the Same) to the right, and the motion of the diverse diagonally (i.e. across the rectangular figure from corner to corner) to the left. And he gave dominion to the motion of the same and like, for that he left single and undivided; but the inner motion he divided in six places and made seven unequal circles having their intervals in ratios of two and three, three of each, and bade the orbits proceed in a direction opposite to one another; and three (Sun, Mercury, Venus) he made to move with equal swiftness, and the remaining four (Moon, Saturn, Mars, Jupiter) to move with unequal swiftness to the three and to one another, but in due proportion.

These are, of course, the numbers in the Platonic Λ:

           1

        2     3
       
     4           9

  8                 27

Check out the video here, as well as the radio show:

• David Kestenbaum, Building a baby earth to test its magnetic field, June 2, 2008.

People who don't get jobs like that may want to spend time in a media immersion pod. Ever tried that? Not me. But lots of people have:

• Virginia Heffernan, In Tokyo, the new trend is 'media immersion pods', New York Times, May 14, 2006.

A little quote:

[...] the Gran Cyber Cafés are enshrouded in the urgent, furtive atmosphere of a hot-sheet motel. Eyes averted, customers sign in, head to the library of entertainment options, and load up on fashion magazines, video games and DVD's of "24" as if stocking up on Jim Beam. Then they beetle-brow it to their solitary pods.

What they do there is up to them. Some people channel-surf. Others trade stocks. You can download music, read novels, watch pornography, play video games, have sex, go to sleep.

According to Mr. Isshow, Japan's "petit iede," or little runaways, come for downtime, free lattes and smoothies, and, at some branches, showers. They use the places as trial separations from home — staying a few hours, overnight or a few days, long enough to scare their parents. (A "night pack" allows use of the pod from 11 p.m. to 8 a.m. for about $10; some places sell toothbrushes and underwear too.) Periodically the management will remind a customer that the cafe is not a hotel, but above all they respect people's privacy.

On a recent afternoon, at around 5:30, I visited the Gran Cyber Café in the Shinjuku neighborhood for the first time, to read e-mail and visit a news site or two. Checking in, I was assigned to pod 16-A.

I loved 16-A the instant I saw it. I closed the door, slipped into a low-slung leatherette seat and surveyed the all-you-can-eat tech feast, which includes VHS and DVD players, satellite and regular television on a Toshiba set, PlayStation 2, Lineage II and a Compaq computer loaded with software, all the relevant downloads and hyperspeedy Internet. In the nearby library were thousands of comic books, magazines and novels. On the desk was a menu of oddball snacks, like boiled egg curry and hot sandwich tuna.

The atmosphere is airless and hot, with a permanent cloud of cigarette smoke. Over all the effect is of a low-wattage, low-oxygen casino.

When I spoke to Japanese cultural critics about the Gran Cyber Cafés, most gave high-flown theoretical accounts of their appeal. But Takami Yasuda, a professor at the School of Informatics and Sciences at Nagoya University who writes about virtual reality, shrugged. "I do not know exactly why people, young guys in particular, love to stay in such a dark place," he said.

I don't know exactly why I stayed either. But 10 books, two DVD's, seven magazines, two newspapers and a video game later, I found that eight hours had elapsed.

• Brooke Gladstone and Bob Garfield, Space odyssey, On the Media, National Public Radio, May 30, 2008.

June 4, 2008

I've been enjoying watching baby birds practice flying, launching themselves off the palm tree in our front yard and awkwardly winging around while chirping in a cute, childish way.

The year before last, a nest of hawks occupied that tree, so we got to see baby hawks fly about and practice diving, sometimes pretending to attack their parents. Last year it was owls: at night we could hear hooting, and see vague white shapes doing strange things. This year I don't know what kind of baby bird I'm seeing. It's annoying. A mockingbird, maybe?

Mockingbirds are one of the dominant bird species here, energetic and intelligent, endlessly inventive in their song as they sit on a nice tree or rooftop. I love listening to them: they usually sing the same phrase three times in a row, then modify it and sing the new phrase three times, and so on, for hours. Usually you'll hear one nearby and another further away — presumably males battling it out, trying to impress the females with their talent. They're the most active in the morning, but in the spring they also sing starting right around midnight. I'm not sure why. But, it always makes me think of that old Elvis song:

Hey, I hear the baby birds chirping now! I've got to go out and take a look.

June 6, 2008

It's late at night — midnight, in fact — and a mockingbird is singing away madly in front of my office. What is it trying to prove? Maybe that it's well-fed and energetic, with lots of time to kill.

My student Alex Hoffnung passed his oral today, and can now officially start work on his thesis. Yay!

I'm working on the talks I'll be giving in Europe. The first will be at 10 am the Monday after next, June 16th, at the workshop on Categorical Groups in Barcelona. I'll talk about my work with Danny Stevenson on classifying spaces for 2-groups. My former student Derek Wise, now a postdoc at U. C. Davis, will talk about representations of 2-groups on 2-Hilbert spaces. Bruce Bartlett, whom I feel a kind of avuncular academic relationship to, will be speaking on representations of 2-groups on finite-dimensional 2-Hilbert spaces. Eugenia Cheng will also be there. Derek has never met these other great pals of mine, so I'm looking forward to that.

Plus, I've never been to Barcelona. I've read that it's the coolest city on the planet! So, it should be fun. I wish I could spend months there and get to know it... but I'll only stay a week and then go to Granada, where I'll hook up with Lisa. I've got to remember to get tickets to the Alhambra. That'll be great.

But right now I've got to prepare talks. Actually, right now I've got to sleep.

June 9, 2008

Okay, I've got one talk done — Classifying Spaces for Topological 2-Groups, for the Categorical Groups conference in Barcelona. I also have my talk ready for the next conference in Barcelona, namely Homotopy Theory and Higher Categories. I'll do that one on a blackboard, so I don't need to make slides — and I've already given this talk once. But now I want to prepare my talk for Algebraic Topological Methods in Computer Sciences III, which will take place sometime during July 7th-11th In Paris.

It's a hectic nuisance now, but if I get all these talks ready now, I can enjoy myself when I'm actually visiting these wonderful places, meeting people and seeing old friends.

Here's an interesting article by a traveler who urges us not to destroy delicate ecosystems by engaging in so-called "ecotourism":

• Dan Neil, Please don't go, Los Angeles Times, June 1, 2008.

• Sarah Handel, No reservations, Blog of the Nation, June 9, 2008.

(We wound up having dinner with Chenchang Zhu and a friend of hers — they're here for another conference, on integrable systems. After dinner they walked over to the sea, but I went to bed. I met Adrian Ocneanu in the lobby — he's developing an interesting generalization of Lie algebras, and maybe of quantum groups, by generalizing the McKay correspondence from quantum SU(2) to other quantum SU(n)'s. One gets a more general notion of "Dynkin diagram"; I found pictures of SU(3) examples on page 18 of Jean-Bernard Zuber's review article.)

June 16, 2008

• Sjoerd Nienhuys, The Beehive charcoal briquette stove in the Khumbu region, Bioenergy Lists: biomass cooking stoves.

Still, it's great a place to visit, listen to talks about categorical groups, and speak with friends. I described some of the talks in week266. I had some really productive conversations with Derek Wise and Bruce Bartlett — we're starting to understand more deeply the beautiful geometry behind representations of 2-groups on higher Hilbert spaces. I'm tempted to include this new understanding in our paper, but it's taken forever to write already. Oh well.

Chenchang Zhu, with Carles Cascabuerta talking to student in background

Timothy Porter and Bruce Bartlett

Aurora del Río, Alain Rousseau, Pilar Carrasco and André Joyal
(photo by Tim Porter)

Derek Wise, John Baez and Bruce Bartlett at La Pedrada
(photo by Mathieu Anel)

June 18, 2008

Scene atop La Pedreda

Apartments in Barcelona

I'm staying in the Residència d'Investigadors southeast of the Plaça Catalunya. What language is this? Català! — or as I would usually say, Catalan. Yes, Barcelona is the thriving heart of Catalonia. I've been interested in Catalan and other lesser-known Romance languages ever since my visit to Nice, where I bumped into traces of the Occitan dialect called Nissart.

Near the Residència d'Investigadors there's a rest home for cats recovering from surgery... or so I've been assured, though one of my email correspondents remains dubious. All I actually saw was a fenced in yard full of listless cats next to the hospital:

Then a few of us — Bruce Bartlett, Tim Porter, Alain Rousseau and a student of Bertrand Toen named Mathieu Anel — went to a bar. Mathieu took us to a bar famous from Hemingway's writings. Sadly, it was closed, so we walked on through increasingly seedy areas to find another. It was around 11 pm; some women who looked like prostitutes were displaying their wares, but many more people were standing or sitting on the sidewalks talking in small groups, shabby but not obviously disreputable. Guys were carrying around sixpacks of red cans, trying to sell what I inanely assumed was some sort of cola, but in fact beer. Not the sort of scene I'm used to. We found a bar with a soccer game on the TV in a back room but a reasonable place to talk in front. Tim Porter immediately went home, tired, but the rest of us talked politics and math until 1. On our way back we found the Hemingway bar was open and packed. We considered going in, but there was a bouncer in front regulating the inflow, and I was tired, so we decided not to.

June 22, 2008

For me it's a joy to be in an urban environment dominated by some bird other than the pigeons and sparrows typical of American cities. I'm not a pigeon-hater: I commend their adaptability! I don't think they should be poisoned. But, they need some predators to keep their population under control.

Lately peregrine falcons have been moving into some urban environments, nesting on tall buildings and feeding on pigeons. Tim Porter, an avid bird-watcher, says there are six peregrine falcons in Barcelona. Each eats just one pigeon a day. That's not much! Will the falcon population increase until they make the pigeon population drop, or is there some other factor limiting the spread of falcons? Perhaps lack of suitable nesting spots?

June 23, 2008

The address of this place is Tendillas de Santa Paula 4, near the intersection with Calle de San Jeronimo, a few blocks from the Monasterio de Santa Paula. I hear the owner has a sister who runs a similar place called La Tana on Calle Rosario 9. Apparently they're both experts on flamenco and eager to talk about it (if you know Spanish).

June 25, 2008

While touring the Alhambra, I became fascinated by the hydraulic technology so crucial to making this place what it is: a paradise of fountains, streams and gardens. Water was originally collected in cisterns and also carried up by hand... but the Alhambra bloomed only after Roman aqueduct technology was adapted to bring water from River Darro to water the gardens. The Arab name for an irrigation canal is "as-saqiya" in Spanish this became "acequia", and the dry regions of the New World once dominated by Spain still have elaborate acequia systems. At the Alhambra, construction of the Acequia Real was began sometime after Ibn Al-Nasr, founder of the last Muslim dynasty in Andalusia, worked out a a desperate deal with Ferdinand III of Castile, who had just invaded Cordoba: Ferdinand could also have Saville if Al-Nasr could keep control of Granada.

Like the Sierras in California, the snow pack in these Sierras is low this year, due to a drought. Pilar Carrasco says they resorted to artificial snow for the ski resorts near Granada this year. Meanwhile, in California, the snow pack started out promising but never got very big: it was a dry spring, and now wildfires are devastating northern California. Naturally I suspect global warming.

June 26, 2008

Lisa and I are getting into the habit of taking siestas after lunch, since it's really hot here during the day, with no air conditioning in most buildings. Then the Spanish habit of having dinner at 9 pm or later makes sense: the sun sets late, but then it cools down and becomes delightfully refreshing, as usual in dry climates.

While lying on the hotel bed in the afternoon, windows shuttered to keep out the blazing sun, sometimes I hear people practicing flamenco guitar or Arabic music. There's a renewed Arab presence in Granada due to immigrants from Morocco, who are very visible working at the falafel and kebab joints lining some streets in the touristy part of town. I hear there's ethnic tenion between them and the Spanish-speaking natives. I don't see much sign of that; the walls around here are covered with graffiti but I can't read most of it.

In the evening we hike along the steep narrow streets looking for good tapas bars, distracted by the views. Note the omnipresent swifts overhead:

In Andalusia, you often get a free tapas with every round of drinks; dinner comes as a gradual side-effect of a night on the town. I've grown to like the roasted green peppers called pimientos del Padrón. Some people call these "Russian roulette" peppers. Most are mild, but supposedly one in ten is hot. However, I've only hit a single hot one in all my munching so far, and even that wasn't bad. Of course, I'm half Mexican and not easily impressed by hot foods.

Another great discovery was a drink called pacharan, which is made by soaking sloe berries, coffee beans and a vanilla pod in anisette. It's got a great flavor, and not terribly strong.

But when it's hot, there's nothing like cerveza con limón.

June 27, 2008

Earlier this week we picked up some CD's from a great little store. They're mostly put out by the obscure but magnificent Pneuma label. Lisa had already gotten ahold of one on her previous visit:

• Eduardo Paríagua and El Arabí Trio, El Agua del Alhambra, Pneuma.

My favorite of the new crop is this one:

• Eduardo Paríagua, Waifr Sheik, Jamila Ghalmí and Luis Delgado, Jardín de Al-Andalus, Pneuma.

The album is peppy but gentle, mostly instrumental, dominated by lute but often backed by percussion. It features Wafir Sheik on lute, viola and other string instruments, Luis Delgado on percussion, and Eduardo Paríagua on flute, ney, flauta de caña and various still more obscure instruments, including percussion. The occasional singing is by Jamila Ghalmí.

June 29, 2008

Now I know the band they'll hire to play in hell.

When the alarm rang, we groggily found our way to the SERHS Campus Hotel on the campus of the Universitat Autonoma de Barcelona (UAB) in Bellaterra, a suburb 18 kilometers north of Barcelona. The hotel refused to serve us lunch, even though there was a big buffet and lots of free tables: they said we needed to make reservations ahead of time. They also refused to fix the broken wireless internet, saying it was the responsibility of the campus — and refused to give us a phone number for the campus, saying they'd contact the relevant officials themselves.

Later we discovered that this hotel is run by students at the hotel management school of the UAB.

Goodbye, Granada!

Granada: view from the Carmen de la Victoria

For my July 2008 diary, go here.