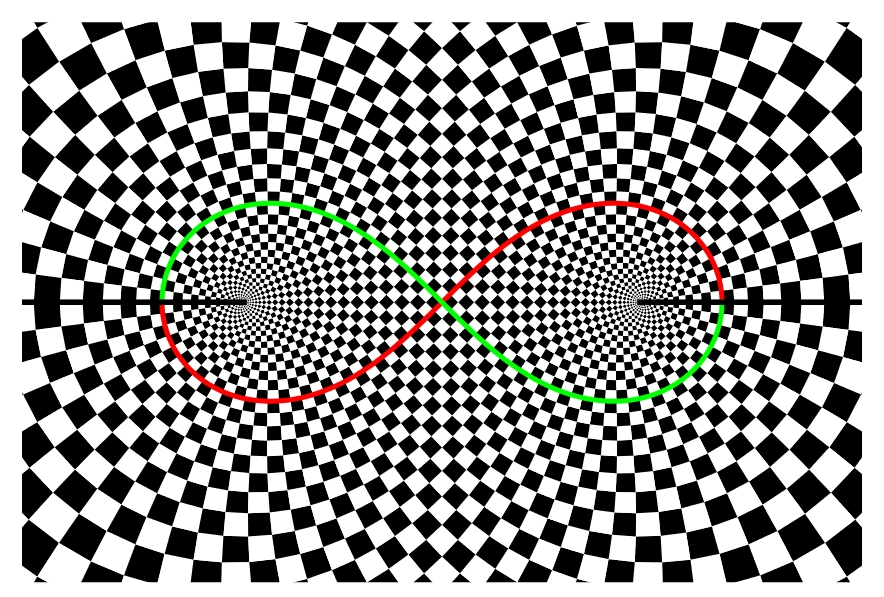
If you map a square conformally onto the plane with two slits cut out, in the nicest way possible, the two lines cutting the square into 4 smaller squares get mapped to 'Bernoulli's lemniscate' — a charming curve shaped like a figure 8.
I didn't really want to know this. But I was studying Bernoulli's lemniscate!
Take 2 points. Draw the curves where the product of the distances from these 2 points is constant. These are called the ovals of Cassini. They look like this:

The one shaped like a figure 8 is special: it's called the lemniscate of Bernoulli.
Or: take a hyperbola \(x^2 - y^2 = a^2\) and 'turn it inside out', replacing each point with polar coordinates \((r,\theta)\) by the point \((1/r,\theta)\). You get Bernoulli's lemniscate!

I didn't want to know any of this! All I wanted to understand is how the lemniscate is connected to the elliptic curve given by \(\mathbb{C}\) modulo the lattice of Gaussian integers. Wikipedia doesn't explain it quite well enough for me, but here's something it says:

In my quest to understand the connection between Bernoulli's lemniscate and elliptic curves, I ran into this great article:
It says a lot about the lemniscate, number theory and elliptic curves. But I'm still confused.
The picture at the start of this entry came from here:

I just learned that there's a number \(\varpi\) that's a lot like \(\pi\).
Just as \(2\pi\) is the circumference of the unit circle, \(2\varpi\) is the perimeter of a curve called Bernoulli's lemniscate. There's even a whole family of functions resembling trig functions with period \(2\varpi\)!
The lemniscate sine and cosine functions look a lot like the usual sine and cosine. They have period \(2\varpi\) instead of \(2\pi\), so here we compare \(sin(2\pi x/\varpi)\), which also has period \(2\varpi\).
The lemniscate sine and cosine functions obey mutant versions of the usual trig identities! For example: $$ \mathrm{sl}^2 x + \mathrm{cl}^2 x = 1 - \mathrm{sl}^2 x \, \mathrm{cl}^2 x $$ and they have derivatives $$ \frac{d}{dx} \mathrm{sl} x = - (1 + \mathrm{sl}^2 x) \mathrm{cl} x $$ $$ \frac{d}{dx} \mathrm{cl} x = - (1 + \mathrm{cl}^2 x) \mathrm{sl} x $$ It's easier to define their inverses:
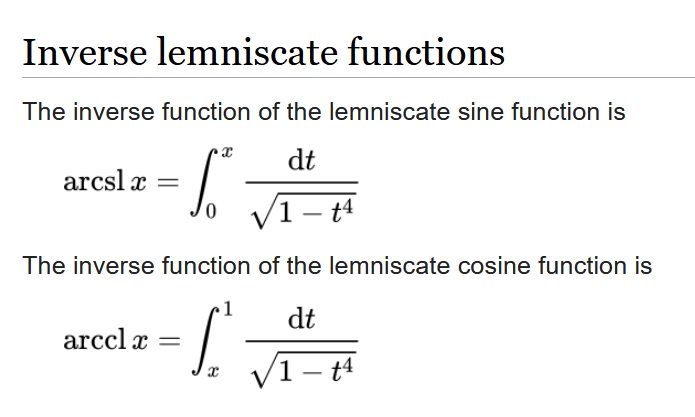
The lemniscate versions of trig functions are examples of 'elliptic functions'. The Weierstrass elliptic function and Jacobi elliptic functions are more familiar — but the lemniscate elliptic functions are actually a special case of the Jacobi elliptic functions.
This page is like looking into a closet and discovering a whole new world:
However, we do know that \(\pi\) is transcendental — and so is its partner \(\varpi\).

But wait — could \(\varpi\) be just \(\pi\) times some rational number?
No. And in 1975, Gregory Chudnovsky showed much more: π and ϖ are algebraically independent. That is: no nonzero polynomial with integer coefficients \(P(x,y)\) has \(P(\pi,\varpi) = 0\).
Later the Chudnovsky brothers became famous, in part because of this funny New Yorker article about their computations of pi:
Gregory Chudnovsky's proof that \(\pi\) and \(\varpi\) are algebraically independent was first announced in a very short abstract in the AMS Notices:
How do people prove numbers are transcendental? It's not easy. It started in 1844 when Liouville showed that an algebraic number can't be extremely well approximated by rationals unless it is rational. For example, $$ 0.1100010000000000000000010000000\dots $$ is transcendental, where there's a 1 in each \(n!\)th decimal place.
The proof is here:
This stuff is hard. Click here for a list of numbers that are believed, but not known, to be transcendental. Baker's Transcendental Number Theory seems like a good book to learn techniques, but I haven't gotten too far into it. For an overview, go here:

The integrals for \(\pi\) tend to have \(x^2\) in them, while those for \(\varpi\) have \(x^3\) or \(x^4\) instead. That's because integrals for \(\pi\) are connected to circles and trig functions, while those for \(\varpi\) are connected to Bernoulli's lemniscate and elliptic functions.
On Twitter, Leo Stein took up my challenge of generalizing these formulas and finding new numbers that are like \(\pi\) in some sense.
First, following this paper:
Next, Leo showed
$$ \int_0^1 \sqrt{1 - x^{2k}} \, dx =
\frac{k}{k+1} \int_0^1 \frac{dx}{\sqrt{1 - x^{2k}}} $$
using integration by parts with \( u = \frac{\sqrt{1 - x^{2k}}}{x^k}\)
and \(dv = x^k dx\). Taking \(n = 2k\) this gives
$$ \varpi_n = \frac{2(n+2)}{n} \int_0^1 \sqrt{1 - x^n} \; dx $$
Leo also showed
$$ \int_0^1 \frac{dx}{\sqrt{1 - x^{2k}}} =
\frac{1}{2} \int_0^1 \frac{dx}{\sqrt{x - x^{k+1}}} $$
using the substitution \(u = x^2\). Taking \(n = 2k\) again
this gives
$$ \varpi_n = \int_0^1 \frac{dx}{\sqrt{x - x^{\frac{n}{2} + 1}}} $$
I could have made mistakes here. Anyway, we seem to be getting
$$ \varpi_n = 2 \int_0^1 \frac{dx}{\sqrt{1 - x^n}}
= \int_0^1 \frac{dx}{\sqrt{x - x^{\frac{n}{2} + 1}}}
= \frac{2(n+2)}{n} \int_0^1 \sqrt{1 - x^n} \; dx
$$
As a sanity check let's take \(n = 2\). Since \(\varpi_2 = \pi\) this
gives
$$ \pi = 2 \int_0^1 \frac{dx}{\sqrt{1 - x^2}}
= \int_0^1 \frac{dx}{\sqrt{x - x^2}}
= 4 \int_0^1 \sqrt{1 - x^2} \; dx
$$
Correct! As another sanity check let's take \(n = 4\). Since
\(\varpi_4 = \varpi\) this gives
$$ \varpi = 2 \int_0^1 \frac{dx}{\sqrt{1 - x^4}}
= \int_0^1 \frac{dx}{\sqrt{x - x^3}}
= 3 \int_0^1 \sqrt{1 - x^4} \; dx
$$
Also correct! Now for something new: let's do the case in between,
\(n = 3\). We get
$$ \varpi_3 = 2 \int_0^1 \frac{dx}{\sqrt{1 - x^3}}
= \int_0^1 \frac{dx}{\sqrt{x - x^{5/2}}}
= \frac{10}{3} \int_0^1 \sqrt{1 - x^3} \; dx
$$
For a less odd case, let's try \(n = 6\). This gives
$$ \varpi_6 = 2 \int_0^1 \frac{dx}{\sqrt{1 - x^6}}
= \int_0^1 \frac{dx}{\sqrt{x - x^4}}
= \frac{8}{3} \int_0^1 \sqrt{1 - x^6} \; dx
$$
June 13, 2022
Take the numbers √2 and 1. Take their arithmetic mean and geometric
mean, getting two new numbers. Take the arithmetic and geometric mean
of those, etc.
You get two sequences of numbers. Both converge to \(\pi\) divided by its evil twin: the lemniscate constant, \(\varpi\).

Gauss showed the arithmetic-geometric mean of \(\sqrt{2}\) and \(1\) is \(\pi/\varpi\) by finding an integral formula for it. This formula is an example of an 'elliptic integral'. You can't do this integral using elementary functions, but Gauss was able to use it to get the job done.

This nice paper explains how Gauss came up with his integral formula for the arithmetic-geometric mean and proved \(\mathrm{agm}(\sqrt{2},1) = \pi/\varpi\):

This simple algorithm let you compute \(\pi\), roughly doubling the number of correct digits with each step! In just 25 steps you get 45 million digits. It uses too much memory to be the most popular, but in 1999 it was used to compute over 200 billion digits of \(\pi\).
The key to the algorithm is that when you compute the arithmetic-geometric mean of two numbers, the number of correct digits doubles with each step. If you also have a quick way to compute the integral shown here, you can use Gauss' formula to compute \(\pi\).

But it's not so easy to explain how the algorithm actually works! After all, it uses the square of the numbers \(a_n\) approximating the arithmetic-geometric mean. So it is not simply computing the arithmetic-geometric mean \(\mathrm{agm}(x,y)\) for \(x = 1, y = 1/\sqrt{2}\), and the integral involving \(x\) and \(y\), and multiplying them to get \(\pi/2\), and doubling that to get \(\pi\). The best explanation I've seen is by one of the algorithm's inventors, Richard Brent:
The Brent–Salamin algorithm computes \(n\) digits of \(\pi\) in almost linear time: \(O(\log n \, M(n))\). Here \(M(n)\) is the complexity of multiplying \(n\)-digit numbers, which was brought down to \(O(n \log n)\) by Harvey and van der Hoeven in 2019.
But in 1988, the Chudnovsky brothers invented a better algorithm for computing pi, based on some formulas of Ramanujan. All recent world records for computing pi use this... including Emma Iwao's 100 trillion digit computation this March!
During the Vietnam war, Grothendieck taught math to the Hanoi University mathematics department staff, out in the countryside. Hoàng Xuân Sính took notes and later did a PhD with him — by correspondence! She mailed him her hand-written thesis.
What was it about?
First, some background. Hoàng Xuân Sính was born in 1933 in a village called Cót, one of seven children of a fabric merchant. Her mother died when she was eight years old, and she was raised by a stepmother.
 This
image of a magazine from 1951 comes with a caption in Vietnamese
saying "Cót village girl is passionate about math". She would
have been 18 at the time.
This
image of a magazine from 1951 comes with a caption in Vietnamese
saying "Cót village girl is passionate about math". She would
have been 18 at the time.
She completed a bachelor's degree in 1951 in Hanoi, studying English and French, and then traveled to Paris for a second baccalaureate in mathematics. She stayed in France to study for the agrégation (the competitive examination for civil service) at the University of Toulouse, which she completed in 1959 before returning to Vietnam and teaching mathematics at the Hanoi National University of Education.
Grothendieck visited North Vietnam in late 1967, during the Vietnam War, and spent a month teaching mathematics to the Hanoi University mathematics department staff, including Hoàng, who took the notes for the lectures. Because of the war, Grothendieck's lectures were held away from Hanoi, first in the nearby countryside and later in Đại Từ. After Grothendieck returned to France, he continued to teach Hoàng Xuân Sính in an exchange of letters.

She finished her thesis in 1972. Around Christmas that year, the United States dropped over 20,000 tons of bombs on North Vietnam, mainly Hanoi. So, it's not surprising that she only defended her thesis three years later, when the North had almost won. But she mentions another reason. She later wrote:
I was a Doctorate student during wartime. Back then, I was teaching at Hanoi Pedagogical University, there was not a mode to take leave to study for Doctorate. I taught during the day and worked on my thesis during the night under the kerosene lamp light. I wrote in French under my distant teacher’s guidance. When I got the approval from France to come over to defend, there were disagreeable talks about not letting me because they was afraid I wasn’t coming back. The most supportive person during the time was Lady Ha Thi Que — President of the Vietnamese Women Coalescent organization. Madame Que was a guerilla, without the conditions to get much education, but gave very convincing reasons to support me. She said, first I am 40 years old, finding work overseas is very difficult, how am I supposed to feed myself; secondly, my kid is here, and no woman would leave their kid. So they should be glad to let me go. I finished my thesis in 1972, and 3 years later with the help and struggle of the women’s organization, I was able to travel over to defend in 1975....
She went to France to defend her thesis at Paris Diderot University (also called Paris 7). Her thesis committee included not only Alexander Grothendieck but also Henri Cartan. Her thesis defense lasted two and a half hours. And soon thereafter she defended a second thesis, entitled "The embedding of a one-dimensional complex in a two-dimensional differential manifold".
She later became the first woman mathematics professor in Vietnam — and the second came 35 years later.
In 1988, she started the first private university in Vietnam, Thang Long University in Hanoi. For a while she was not only the head, but also the janitor, bringing water to the school and sweeping floors. Later she said "When I look back at it, I thought it was the most romantic idea I’ve had."
In 2003 she was awarded France's Ordre des Palmes Académiques. She is still alive! I hope someone has interviewed her, or does it now. Her stories must be very interesting.
But what about her thesis?
Her thesis classified Gr-categories, which are now called '2-groups' for short. A 2-group is the categorified version of a group: it's a monoidal category where every object and morphism is invertible. (An object \(x\) is invertible if there's an object \(y\) with \(x \otimes y \cong y \otimes x \cong I\), where \(I\) is the unit for the tensor product.)
From a 2-group you can get two groups:
Even better, Sính showed that cohomologous 3-cocycles give equivalent 2-groups. (Equivalent as monoidal categories, that is.)
So, we can classify 2-groups using cohomology! The most exciting, least obvious part of this is the cohomology class \([a] \in H^3(G,H)\). This is often called the 'Sính invariant'.
This connection between 2-groups and cohomology is no coincidence. It's best understood using a bit more topology.
Any connected space with a basepoint, say \(X\), has a fundamental group. But it also has a fundamental 2-group! This 2-group has \(G = \pi_1(X)\) and \(H = \pi_2(X)\). And if all the higher homotopy groups of \(X\) vanish, this 2-group knows everything about the homotopy type of \(X\), at least if \(X\) is reasonably nice, like a CW complex.
So, Sính's thesis sheds light on 'homotopy 2-types': that is, homotopy types of nice spaces with \(\pi_n(X) = 0\) for \(n > 2\). They are just 2-groups!
Sính's thesis illuminated one of the simplest — yet still important — special cases of Grothendieck's 'homotopy hypothesis', namely that homotopy \(n\)-types correspond to \(n\)-groupoids.
You can see Hoàng Xuân Sính's thesis along with a handwritten summary in English here:
That website also has three nice photos of Grothendieck in Vietnam. I showed a colorized version of one at the top of this article, and here is another, with Sính at far left:
Here are the original uncolorized versions of all three:
I looked at Twitter. I saw that 1.6 miles away, near where Big Springs Road ends in the Box Springs park, there had been a rapidly spreading fire.


Luckily the fire department had already sent in 2 engines, 2 bulldozers, 2 hand crews and 2 chief officers. They stopped the blaze when it was 3 acres in area, then stayed there for hours putting it out completely.
Whew!
Here is a video of the fire:
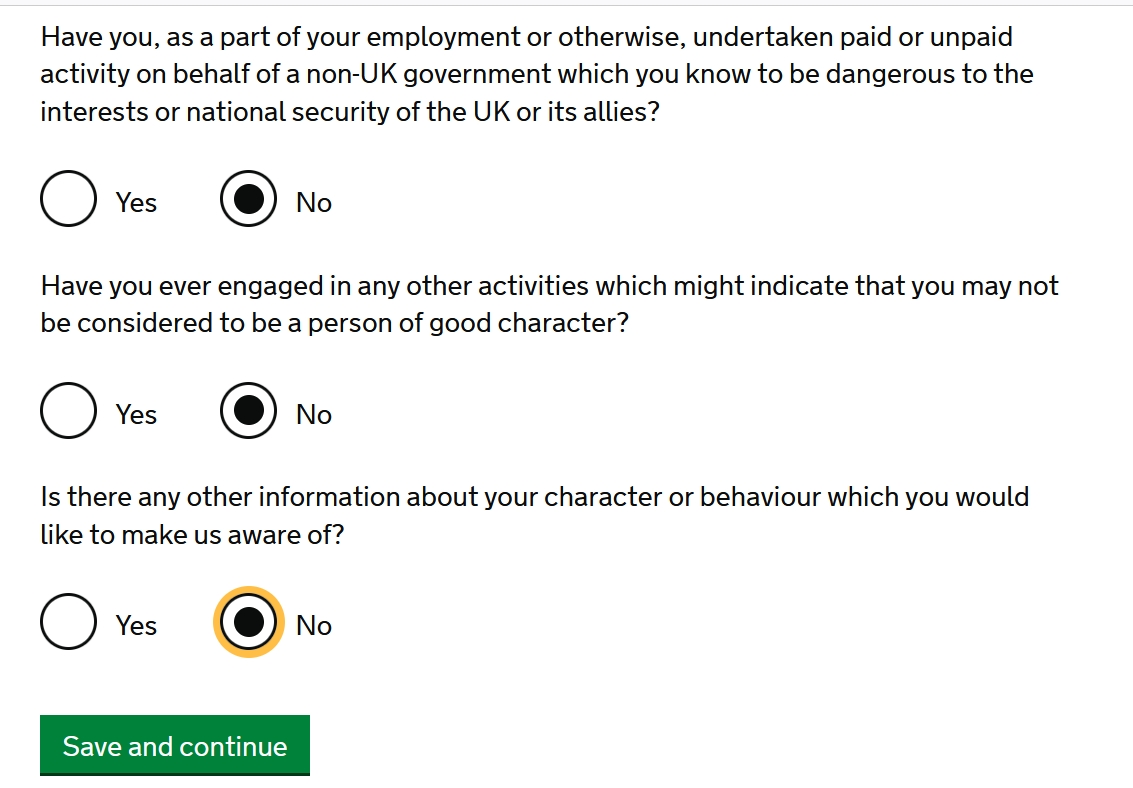
But some were much worse. I repeatedly filled out the application saying Lisa was my dependent, but when it came time to apply for health insurance I was asked to confirm that I had no dependents:
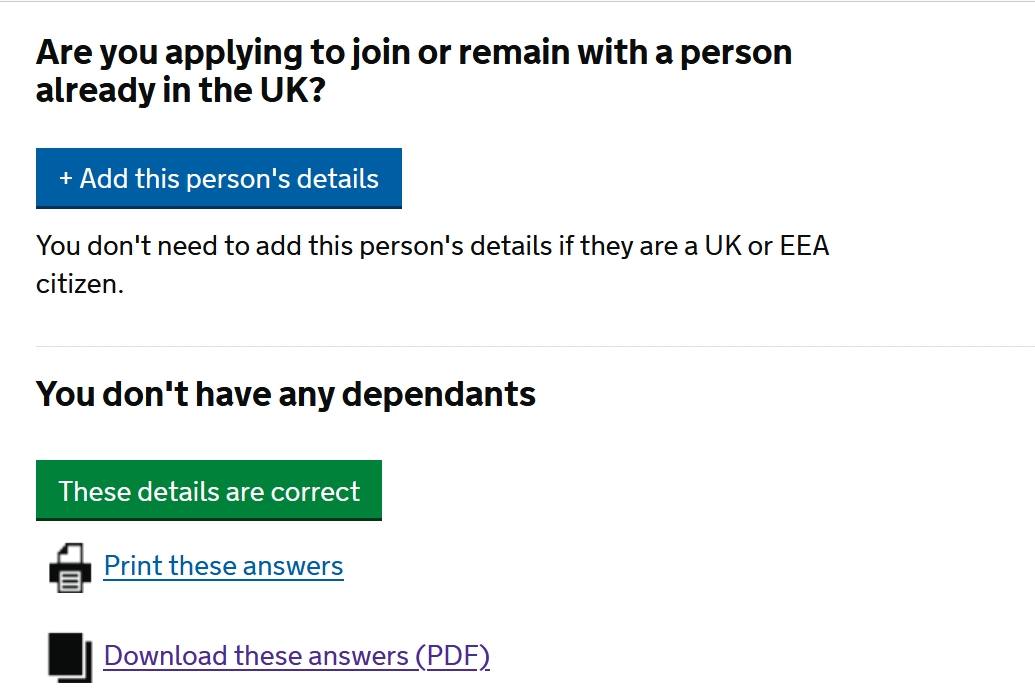
There was no option given except to agree. And then I was taken to a page that sternly warned me I could be committing perjury if I didn't tell the truth!
Again there was no option except to agree. I wound up calling a UK visa help line. After waiting 30 minutes, I got someone whose phone wasn't working well — after I described my problem, I couldn't hear what she said. I called back and again and got someone audible. After I explained my problem, he looked it up and said "Yes, people have reported that bug in the software. Just go ahead and ignore it."
There was more. After getting my biometric taken by Homeland
Security, I sent my passport to Flushing, New York where my visa
will be physically attached to it, and then they should send it back.
There is no way to know how long this will take, or how it's going
since they received it. At least they sent me an email saying they
received it.
June 30, 2022
There's been a lot of stressful news these days — the new
revelations about Trump, the Supreme Court decision overturning Roe
v. Wade, the continuing war in Ukraine, and so on — so I'd just
like to point out that you can cut a bagel in half using two Möbius
strips:
And believe it or not, this is actually kind of important in math.
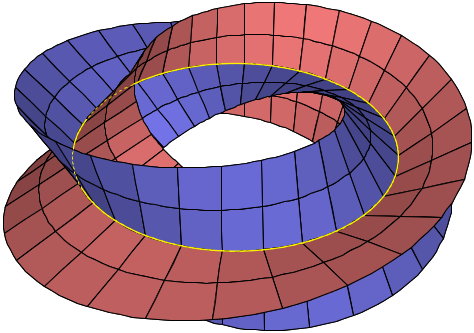
For each point on a circle in 3d space, there's a plane through this point that cuts the circle at right angles. Each such plane is a 2d real vector space. So we get a '2-dimensional real vector bundle over the circle'.
A bagel is a sad approximation of this, where instead of planes we have disk-shaped bagel slices.
We can draw two coordinate axes in each of these planes, and let these axes twist as they go around. This says our 2d real vector bundle is a 'direct sum' of two 1d real vector bundles, called Möbius strip bundles.
The Möbius strip bundles are 'nontrivial' — they have a topological twist that can't be undone. But our 2d real vector bundle (the bagel bundle) is 'trivial' — it has no twist.
The direct sum of two nontrivial 1d real vector bundles over the circle is trivial!
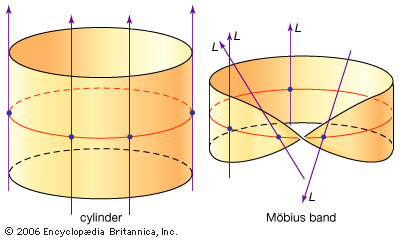
Write \(M\) for the Möbius strip bundle, and \(T\) for the trivial 1d real vector bundle over the circle, which looks like the cylinder shown above. Then we've seen $$ M \oplus M \cong T \oplus T$$ since \(T \oplus T\) is the trivial 2d real vector bundle over the circle.
In fact every real vector bundle over the circle is isomorphic to a direct sum of copies of \(M\) and \(T\), and $$ M \oplus M \cong T \oplus T$$ is the only interesting relation that holds. This puts us in a great position to understand the 'real K-theory' of the circle.
To get the real K-theory of the circle, take the set of isomorphism classes of real vector bundles over a circle, which is a commutative monoid using \(\oplus\), and throw in formal inverses to get an abelian group. You get the abelian group generated by \(M\) and \(T\) with $$ M + M = T + T $$ What's this abelian group? I'll let you figure out a more standard name for it. But we've seen how cleverly slicing bagels helps us understand the real K-theory of the circle! For more, try this: