Famous mathematician and Bourbaki member Pierre Cartier has some great stories. Like how Grothendieck got kicked out of a math conference for handing out revolutionary leaflets. He moved out to the street to do it there, but there was a law against that. The guy who kicked out Grothendieck was Dieudonne, the official note-taker and editor of Bourbaki. He and Grothendieck got along at first, but then had a falling-out.
And Dieudonne had a hot temper! Once he dramatically ripped up a Bourbaki book in progress...
... which led to this scene: two famous mathematicians under a table, trying to rescue the ripped fragments of a manuscript. Cartier has a knack for acting out these scenes.
The whole interview is below. Anecdotes about Grothendieck and Bourbaki start around 11:23. It's in French with English subtitles. Unfortunately the English subtitles leave out some of the fun.
The electromagnetic field says how the phase of a charged particle changes when it moves around a small square in spacetime. The electric field deals with squares in the \(xt\), \(yt\) and \(zt\) directions, while the magnetic field handles the \(xy\), \(yz\) and \(zx\) squares.
Suppose we lived in Flatland, with just 2 dimensions of space and one of time, and coordinates \(t,x,y\). Then the electric field would have 2 components to handle \(tx\) and \(ty\) squares. But the magnetic field would have just one, \(xy\).
Or suppose we lived in Lineland, with just one dimension of space and one of time, and coordinates \(t,x\). Then the electric field would have just one component, to handle phase change around \(tx\) squares. And there would be no magnetic field! It would not exist.
Or suppose we lived in a universe with 4 dimensions of space, say \(w,x,y,z\), and one dimension of time, \(t\). Then the electric field would have 4 components: $$ tw,tx,ty,tz $$ while the magnetic field would have 6: $$ wx,wy,wz,xy,xz,yz $$ The magnetic field starts winning!
You can work out the pattern and show that if time is 1-dimensional, the electric and magnetic fields have the same number of components only when space is 3-dimensional! In this situation, which is our lovely universe, we get 'electromagnetic duality'. I explained this in a different way in my March 29 diary entry:
When spacetime is 4-dimensional, electromagnetic duality switches the electric and magnetic fields. Geometrically it comes from something called the 'Hodge star operator', which maps each little square to its orthogonal square: for example, \(tx\) to \(yz\).
Professionals say it this way: in 4d spacetime, the Hodge star
operator sends bivectors to bivectors. Dually, it sends 2-forms to
2-forms. So it sends the electromagnetic field F to a new 2-form
called \(\star F\), where the electric and magnetic fields are switched!
May 9, 2022
We can write Maxwell's equations using:
I won't explain it all now, but the \(\star\) operator applied to the electromagnetic field switches the electric and magnetic fields $$ E \mapsto B $$ $$ B \mapsto -E $$ because it switches space-time 2-forms like \(dt \wedge dx\) and space-space 2-forms like \(dy \wedge dz\).
The equation \(dF = 0\) unifies the two Maxwell equations that don't involve the charge density \(\rho\) and current density \(\mathbf{J}\). The equation \(d star F = J \) unifies the two Maxwell equations that do.
When the current 3-form J is zero, Maxwell's equations become the simpler 'vacuum Maxwell equations': $$ dF = d\star F = 0 $$ These are symmetric under electromagnetic duality: you can replace \(F\) with \(\star F\), switching electric and magnetic fields.
We can combine \(F\) and \(\star F\) into a single complex-valued 2-form: $$ \mathcal{F} = F + i\star F $$ Then the vacuum Maxwell equations become just one equation $$ d\mathcal{F} = 0 $$ and electromagnetic duality is multiplying by \(-i\).
So a lot is going on here... and I haven't even explained the exterior
derivative operator \(d\). I'm not sure I will. I explained it in my
book Gauge Fields, Knots and Gravity. But it took a while!
The first hundred pages are all about manifolds, differential forms
and Maxwell's equations.
May 17, 2022
Despite many years of searching, physicists have never found a
magnetic monopole: a particle that makes the magnetic field point out
in all directions. Magnetic monopoles are forbidden by Maxwell's
equations. But if we found one, we could change Maxwell's equations
like this:
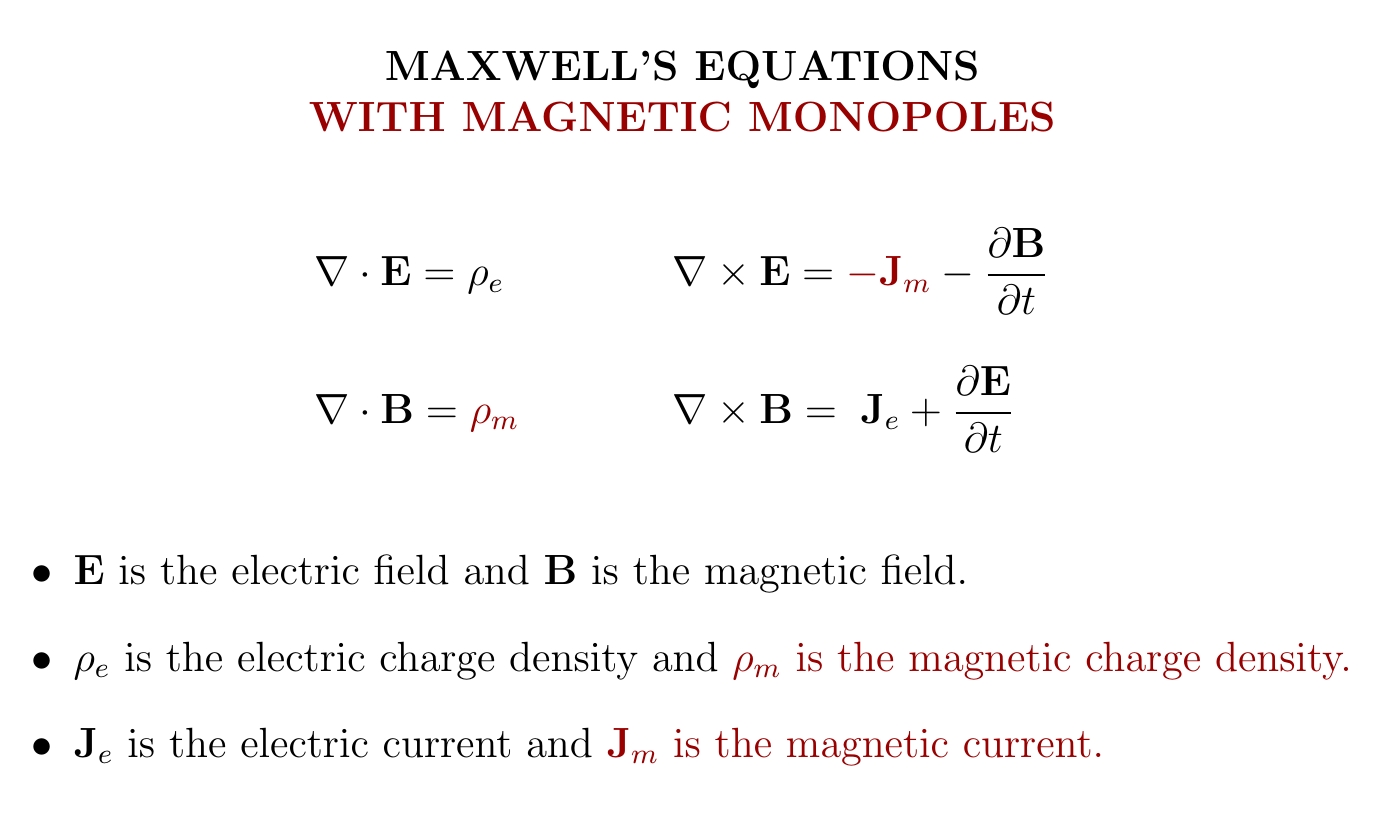
Actually I'm lying slightly. A physics grad student named Blas Cabrera Navarro doing an experiment to search for monopoles seemed to find one on the night of February 14, 1982. It's called the 'Valentine's Day monopole'. But it could have been an error. See this:
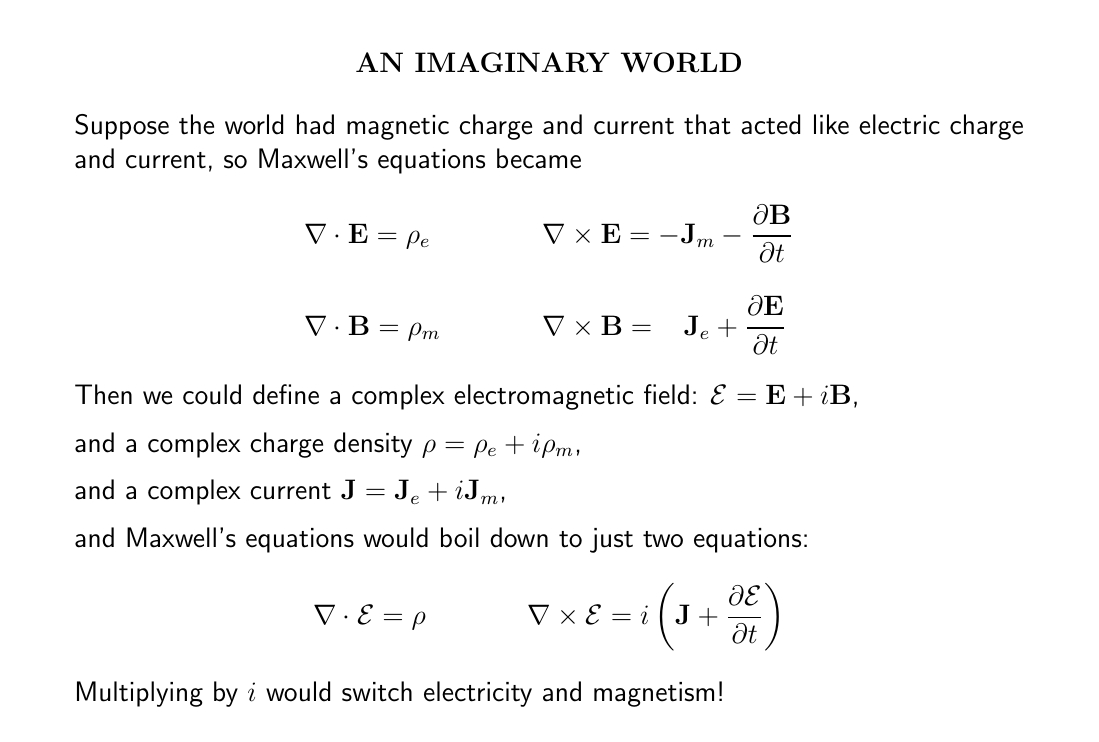
This crazy theory reduces to the usual Maxwell equations whenever there "just happens" to be no magnetic charge and current. And when there's also no electric charge and current — like with light in the vacuum — it's actually useful to combine the \(\mathbf{E}\) and \(\mathbf{B}\) fields.
But the world does not have magnetic charge and current, as best we can tell — and this is a big clue. Thanks to this, we can express electromagnetism in terms of potentials! We could not do this otherwise.
And these potentials are the start of 'gauge theory'.
The vector potential tells us how the phase of a charged particle rotates as the particle moves through space. The scalar potential says how the phase rotates as the particle moves through time! This is the basic idea of gauge theory... as applied to electromagnetism.
I'd love to gently carry my expository diary entries about electromagnetism up to state of the art, but I doubt I will — so let me just dive in and talk about this:
In his famous 1931 paper on magnetic monopoles, Dirac argued that a particle of magnetic charge \(g\) is compatible with a particle of electric charge \(e\) only if $$ e g = 2\pi n $$ for some integer \(n\). This argument works best with some topology, but it's fun to see how Dirac did it before Chern classes.
Later Zwanziger and Schwinger showed a particle of electric and magnetic charge\((e, g)\) is compatible with one of charge \((e', g')\) only if $$ e g' - e' g = 2\pi n $$ The left-hand side looks like the determinant of a \(2\times 2\) matrix, and this is no coincidence!
Then things got deeper. The Georgi-Glashow model is an \(\mathrm{SO}(3)\) Yang–Mills theory coupled to a Higgs field, which spontaneously breaks symmetry leaving a \(\mathrm{U}(1)\) gauge field: electromagnetism. But it has topological solitons... which are magnetic monopoles!
Adding a CP-violating term to the Lagrangian gives an even more interesting theory. This is called a 'theta term'. One puzzle in particle physics is why the strong interaction, described by \(\mathrm{SU}(3)\) Yang-Mills, is lacking a similar term. But here it helps us study dyons.
In statistical mechanics the key function describing any system is its 'partition function' — I'll explain that in a minute. Imagine a gas of 'primons', one for each prime, and say the primon \(p\) has energy \(\ln p\). The partition function of this gas is the Riemann zeta function!
To get the 'partition function' of a system, just sum \(\exp(-E/kT)\) over all states where \(E\) is the energy of the state, \(k\) is Boltzmann's constant and \(T\) is temperature.
If you work this out for the primon gas, you get the Riemann zeta function \(\zeta(s)\) where \(s=1/kT\). Here's why:
It's fun to imagine a canister containing a gas of prime numbers popping in and out of existence, with the energy of a collection like \(2, 2, 3, 7\) being \( \ln(2) + \ln(2) + \ln(3) + \ln(7) = \ln(84) \). From its partition function we can compute its entropy, its specific heat, and so on.
Heat it up! When \(T\) approaches the 'Hagedorn temperature', the partition function diverges as arbitrarily large collections of primons become likely. It's impossible to go above this temperature. This corresponds to the pole of the Riemann zeta function at \(s=1\).
This blog article by students formerly at Australian National University explains the primon gas and computes its energy as a function of temperature. The answer is \(-\zeta'(s)/\zeta(s)\).
So far our primes have been bosons, since we can have as many copies of the same prime as we want in our canister. This blog article explains how the story changes if our primons are fermions... or if we allow both bosonic and fermionic primes:
I gave a talk on motives today at a conference in honor of Grothendieck at Chapman University. You can see slides and a video here:
Grothendieck and Deligne proved the Weil Conjectures using an extra axiom you can add to set theory, the axiom of universes. But when someone asked Grothendieck if this should make us doubt the Weil Conjectures, his response was gruff.
I find this hilarious.
Colin McLarty helped dig up the tapes of Grothendieck's 1973 lectures in Buffalo. He went through them — and discussed them at a recent conference at Chapman. They show that Grothendieck considered the axiom of universes a mere convenience in his work.
Here is a talk McLarty gave about this: