Magnetic Moments

Where do the normal and anomalous Zeeman formulas come from?

First, a bit of classical physics. Imagine an ``infinitesimally small'' bar magnet - this is called a magnetic dipole. A vector (say $\mu$) represents the strength and direction of the dipole; $\mu$ is known as the magnetic moment.

Suppose we place the dipole in a magnetic field B. The field will exert a torque on the dipole, trying to flip it into alignment (so B and $\mu$ are parallel). Twisting the dipole out of alignment takes energy. In other words, the dipole has a potential energy that depends on its orientation with respect to the field. Classical physics says that this ``magnetic'' energy is given by .

A tiny current loop acts like a dipole, with a magnetic moment perpendicular to the plane of the loop. The current loop possesses angular momentum (after all, the current consists of moving charges, which have mass). According to classical physics, the magnetic moment is proportional to the angular momentum: $\boldmath\mu =$ constant times J. The constant depends on the charge/mass ratio of the moving charges making up the current.

We now apply all this to an electron in an atom in a magnetic field. Thanks to its orbital angular momentum l, it has a ``magnetic'' energy proportional to ${\bf B}\cdot{\bf l}$; likewise, the spin contributes energy proportional to ${\bf B}\cdot{\bf s}$. Adding up the l's and s's for all the electrons in the atom, we might expect a formula like this for the total ``magnetic'' energy:

$$E^{\rm mag} = {\rm constant}\, {\bf B}\cdot ({\bf L}+{\bf S}) = {\rm constant}\, {\bf B}\cdot {\bf J}$$

Instead, the correct formula is:

$$E^{\rm mag} = {\rm constant}\, {\bf B}\cdot ({\bf L}+2{\bf S})$$ (6)

Let us accept this formula, noting but not discussing the mysterious factor 2. If we pick the $z$-axis in the direction of B, then the dot product simply pulls out the $z$-component of L and S, times the magnitude of B. The quantum numbers $M_L$ and $M_S$ give the values of these components. So we get the ``normal Zeeman'' formula:

$$E^{\rm mag}_{LM_LSM_S} = {\rm constant}\,B(M_L+2M_S)$$

or equivalently:

$$E^{\rm mag}_{LM_LSM_S} = {\rm constant}\,B(M_J+M_S)$$ (7)

since $M_J=M_L+M_S$.

Without the enigmatic 2, we'd simply have $M_J$ on the right hand side of formula 7. Without $M_S$ on the right hand side, the normal and anomalous Zeeman formulas would be the same-- as we will see.

How does the electron maintain its orientation in the magnetic field-- why doesn't it snap into alignment? Or in ``old quantum'' terms, how can we have stationary states with S (or L) out of alignment with the field? This was a legitimate question for the old quantum theory, and it had a good answer. The spinning electron acts like a gyroscope. The field exerts a torque on the electron, and like any gyroscope, the electron precesses. (The same argument holds for L.)

We can get the ``anomalous Zeeman'' formula from formula 7 with a little vector algebra, and a crucial assumption:

Assume that in any stationary quantum state, S and L each precess around J, so that the projection of S on J doesn't change, but the component of S perpendicular to J rotates uniformly (ditto for L).

This is called spin-orbit coupling. Only without an external magnetic field is it strictly true. It is approximately true if the external field is weak enough. It breaks down in a strong magnetic field, a phenomenon known as spin-orbit decoupling.

Where does spin-orbit coupling come from? Naively expressed, from a torque trying to make L and S point opposite to each other (i.e., anti-parallel). Goudsmit and Uhlenbeck imagined it this way. Suppose there is only a single electron. If we ride along an electron's orbit right next to it, but not spinning ourselves, we will appear to see the nucleus orbiting us (shades of Ptolemy!) Effectively we have a positive current circulating around us; this will generate a magnetic field proportional to L. The electron has a magnetic moment proportional to S, and hence we get an energy term proportional to ${\bf L}\cdot{\bf S}$. (Because of the positive charge on the nucleus, the signs come out so that spin-orbit coupling trys to make L and S anti-parallel.)

Life is more complicated in multi-electron atoms. ${\bf L}\cdot{\bf S}$ is only an approximation, applicable when the electron-electron forces dominate the spin-orbit forces. In this case, one can approximate the totality of electrons as a single electron ``smear'', with total orbital angular momentum L, and total spin S. For ``light'' atoms, this works pretty well. For ``heavy'' atoms, a different approximation works better.

A classical model has emerged. The vectors L and S feel a torque trying to make them anti-parallel; when the magnetic field B is turned on, L and S each feel a torque trying to align them with B. We have, in other words, ``perturbation terms'' occuring somewhere in the total energy formula:

$$c_1{\bf L}\cdot{\bf S} + c_2{\bf B}\cdot({\bf J}+{\bf S})$$ (8)

where $c_1$ and $c_2$ are constants, and S occurs on the right hand side only because of the mysterious factor 2 in formula 6.

Classical mechanics would next try to compute the ``trajectories'' of the vectors L and S (i.e., how they vary with time). If ${\bf B}=0$, then J is constant (conservation of angular momentum), and L and S precess about J. If the field is weak, then (to a good approximation) J precesses about B, while L and S still precess about J. J is no longer constant, since it is subject to an external torque. If the field is strong, then L and S precess about B (again to a good approximation), because the magnetic torque swamps the spin-orbit torque.

The ``old quantum'' prescription says to find the energy levels of these stationary states.

As it happens, the energy of a stationary state depends primarily on terms other than those in formula 8. We have terms analogous to the $R/n^2$ of hydrogen; then terms depending on the magnitude of L and S (i.e., terms depending on $L$ and $S$); only after that does formula 8 come into play.

The spin-orbit coupling contributes a perturbation that depends on the angle between L and S (and hence indirectly on the magnitude of J). So when ${\bf B}=0$, we expect to find bunches of energy levels with the same $L$ and $S$ grouped closely together, separated slightly by an energy difference depending on $J$. This is an aspect of the famous fine structure of the spectrum.¹² If $S=0$, then the fine structure disappears. (Low-lying energy levels of atoms with even numbers of electrons usually have $S=0$.)

Without a field, we have complete rotational symmetry in the energy formula. The spin-orbit perturbation depends only on the magnitude of J, not on its direction (on $J$, not on $M_J$). With a field, the symmetry is broken and the degeneracy lifted.

We have perturbations depending on ${\bf B}\cdot{\bf L}$ and ${\bf B}\cdot{\bf S}$. With a strong field (or if $S=0$), we confidently replace these dot products with $BM_L$ and $BM_S$, for the dot products don't change and must be quantized (i.e., they are stationary). We have seen already how this leads to the normal Zeeman effect. Note also another regularity: spectra without fine-structure have $S=0$, and hence display normal Zeeman splitting.

With a weak field, we express the perturbation in terms of ${\bf B}\cdot{\bf J}$ and ${\bf B}\cdot{\bf S}$. The first term we replace with $BM_J$. Were this all, we would again see a normal Zeeman effect, because $\Delta M_J$ and $\Delta M_L$ satisfy the same selection rule.

Turn to the ${\bf B}\cdot{\bf S}$ perturbation. Because S precesses about J, the average value of ${\bf B}\cdot{\bf S}$ is the same as

$${\bf B}\cdot{\bf S}_\parallel$$

where ${\bf S}_\parallel$ is the projection of S on J. The dot product ${\bf B}\cdot{\bf S}_\parallel$ doesn't change, so it must be quantized. ${\bf S}_\parallel$ is some fraction of J, so this dot product must be some fraction of $M_J$. What fraction? If we knew the lengths of L and S and the angle between them, we'd clearly have enough information to specify the geometry completely. Instead of the angle, we could also use the length of J. So we expect the fraction to depend on $L$, $S$, and $J$. And that, as we've seen, accounts for the anomalous Zeeman effect.

The rest is vector algebra. You may skip to the next section if you like-- no new concepts appear.

First derive a formula for ${\bf L}\cdot{\bf S}$, in terms of quantum numbers. We have:

$${\bf J}\cdot{\bf J} = ({\bf L}+{\bf S})\cdot({\bf L}+{\bf S... ...L}\cdot {\bf L} + {\bf S}\cdot {\bf S} + 2{\bf L}\cdot {\bf S}$$

Rearrange this equation and replace ${\bf J}\cdot{\bf J}$ with $J(J+1)$ (and likewise for L and S), to get:

$${\bf L}\cdot{\bf S}\rightarrow \frac{J(J+1)-L(L+1)-S(S+1)}{2}$$ (9)

where I've used an arrow instead of an equal sign to indicate ``quantization''-- classical quantities on the left, quantum numbers on the right. From the modern perspective, the left hand side is an operator, and the right hand side is one of its eigenvalues. (Formula 9 looks tantalizingly close to the Landé g-factor, but we're not quite there yet.)

Next derive a formula for ${\bf S}_\parallel$, the projection of S on J:

$$\begin{eqnarray*} {\bf S}_\parallel &=& \frac{{\bf J}\cdot{\bf S}}{{\bf J}\cdot... ...ac{{\bf S}\cdot{\bf S}}{{\bf J}\cdot{\bf J}} \right) {\bf J}\\ \end{eqnarray*}$$

``Quantizing'' the term in parentheses:

$$\frac{J(J+1)-L(L+1)-S(S+1)}{2J(J+1)}+\frac{S(S+1)}{J(J+1)}=\frac{J(J+1)-L(L+1)+S(S+1)}{2J(J+1)}$$

In other words, ${\bf S}_\parallel$ is this fraction times J. Taking the dot product with B, we got previously:

$$E^{\rm mag} = {\rm constant}\,B(M_J+M_S)$$

Replace the term $BM_S$ with the ``average'' value of ${\bf B}\cdot{\bf S}$, which is ${\bf B}\cdot{\bf S}_\parallel$, which is the above fraction times $BM_J$:

$$E^{\rm mag} = {\rm constant}\,B(M_J+\frac{J(J+1)-L(L+1)+S(S+1)}{2J(J+1)}M_J)$$

And this reduces to our anomalous Zeeman formula, formula 2.

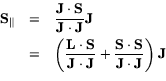
© 2001 Michael Weiss

home