John Baez

Seminar on This Week's Finds

I wrote 300 issues of a column called This Week's Finds, where I explained math and physics. In the fall of 2022 I gave ten talks based on these columns, and I gave eight more in the fall of 2023.

Here you can find videos of these talks, and some lecture notes.

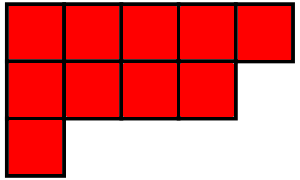
Young diagrams and classical groups

Young diagrams are combinatorial structures that show up in a myriad of applications. Among other things, they can be used to classify conjugacy classes in the symmetric groups \(S_n\), irreducible representations of \(S_n\), and irreducible representations of the classical groups \(\mathrm{GL}(n)\), \(\mathrm{SL}(n)\), \(\mathrm{U}(n)\) and \(\mathrm{SU}(n)\).


Young diagrams; the representation theory of monoids


Classifying representations of the symmetric group \(S_n\) using Young diagrams with \(n\) boxes


The classical groups; classifying representations of the monoid of \(N \times N\) matrices using Young diagrams with \(\le N\) rows

Dynkin diagrams

Coxeter and Dynkin diagrams classify a wide variety of structures, most notably finite reflection groups, lattices having such groups as symmetries, compact simple Lie groups and complex simple Lie algebras. The simply laced or 'ADE' Dynkin diagrams also classify finite subgroups of \(\mathrm{SU}(2)\) and quivers with finitely many indecomposable representations. This tour of Coxeter and Dynkin diagrams will focus on the connections between these structures.


How Coxeter diagrams classify finite reflection groups


How Coxeter diagrams classify root lattices


How Coxeter diagrams classify compact semisimple Lie groups


How Dynkin diagrams correspond to Lie groups of symmetries


\(\mathrm{E}_8\) and the octonions

Quaternions and octonions

There are four normed division algebras: the real numbers, complex numbers, quaternions and octonions. The quaternions are a noncommutative algebra of dimension 4, while the octonions are a noncommutative and nonassociative algebra of dimension 8. Here we explain how to multiply quaternions and octonions using the familiar dot product and cross product of vectors. For the proof that octonion multiplication obeys \(|ab| = |a||b|\), go here:


Quaternions and octonions

The threefold way

Irreducible real group representations come in three kinds, a fact arising from the three associative normed real division algebras: the real numbers, complex numbers and quaternions. Dyson called this the threefold way. The spin-1/2 representation of SU(2) is a great example: it is quaternionic, since SU(2) is isomorphic to the group of quaternions \(q\) with \(|q| = 1\), and the spin-1/2 representation is isomorphic to the space of all quaternions. For more, go here:


The threefold way

The periodic table of \(n\)-categories

Categorification is a not-completely-systematic process of taking known math and replacing sets by categories, functions by functors, and equations by natural isomorphisms. Often categorifying simple results in math leads to deeper, more interesting results. When you iterate the process of categorification you are pushed into the study of \(n\)-categories. These exhibit striking patterns visible in the "periodic table" of \(n\)-categories, such as the Stabilization Hypothesis. I'll concentrate on sketching the basic ideas, since the evidence is much easier to explain than the rigorous proofs. This is an elementary introduction to higher categories. For more, go here:


An elementary introduction to \(n\)-categories


The periodic table of \(n\)-categories


Topology and the periodic table of \(n\)-categories

The 3-strand braid group

The 3-strand braid group has striking connections to the group SL(2,Z) of invertible 2x2 matrices with integer entries, the Lorentz group from special relativity, modular forms, and the trefoil knot. They all fit together in a neat package, which I explain here.


The 3-strand braid group

Combinatorics and categorification

The theory of generating functions is a simple and fun but powerful tool in enumerative combinatorics, which I will explain in the next few lectures. Digging into it, we shall see that it rests on some ideas from 'categorification': the more or less systematic replacement of sets by categories. One is 'groupoid cardinality': just as finite sets have cardinalities that are natural numbers, finite groupoids have cardinalities that are nonnegative rational numbers! Another is Joyal's theory of species. A species is a type of structure that can be put on finite sets, of the sort we count in enumerative combinatorics. Just as polynomials in one variable form the free ring on one generator, the category of species is the free '2-rig' on one generator, a 2-rig being a categorified analogue of a rig. I will explain these ideas with a minimum of prerequisites.

My talks will be very loosely based on this paper:

And here's some more reading material — free books:

Groupoid cardinality and species


Species and their generating functions

Categorifying the quantum harmonic oscillator

In my last lecture on combinatorics and categorification, I describe an application to quantum mechanics. Classically, light in a mirrored box can be described as a collection of harmonic oscillators, one for each vibrational mode of the light. Planck 'quantized' the electromagnetic field by assuming that energy of each oscillator could only take on discrete, evenly spaced values. Later Einstein took this seriously, and realized that light comes in discrete energy packets called 'quanta'. Surprisingly, when we categorify the mathematics describing this situation we are led to the theory of 'species' — one of the basic tools of combinatorics. A species is any type of structure we can put on finite sets. The commutation relations between annihilation and creation operators, and the inner product on the Hilbert space of a quantum harmonic oscillator, then receive a natural interpretation in terms of species.


Categorifying the harmonic oscillator

© 2022-2023 John Baez
baez@math.removethis.ucr.andthis.edu

home