

Dobiński's formula is not the easiest way to count the partitions of an n-element set, but it's beautiful.
Say it's raining and raindrops land randomly on your head at an average of one per minute. Suppose the raindrops are independent.
What's the probability that \(k\) raindrops land in \(M\) minutes? The answer is called a "Poisson distribution of mean \(M\)".
If on average one raindrop hits your head per minute, the probability that exactly \(k\) drops hit your head in \(M\) minutes is $$ \frac{e^{-M} M^k}{k!} $$ This is the Poisson distribution of mean \(M\).
Now let's look at one minute, so we get the Poisson distribution of mean \(M = 1\): $$ \frac{1}{e k!} $$ The 'first moment' of this distribution is just the average number of raindrops that hit your head in a minute. It's \(1\).
The 'second moment' is the average of the square of the number of raindrops that hit your head in a minute. This is less obvious: it's \(2\).
The 'third moment' is the average of the cube of the number of raindrops that hit your head in a minute. This is \(5\).
In general, the \(n\)th moment of the Poisson distribution with mean \(1\) is the number of partitions of an \(n\)-element set. That's what Dobiński's formula says! I gave a proof here, as part of a series on random permutations:
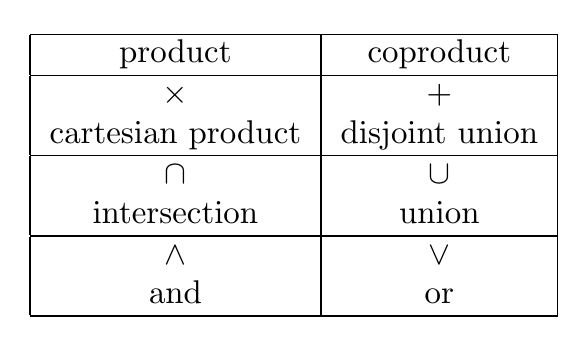
Category theory unifies and clarifies our concepts. For example, in any category we can define the concepts of "product" and "coproduct". Let's see how they work in examples!
So, + is just like × with the direction of the maps reversed!
So, the definition of union is just like that of intersection with the "subset" relation turned around!
So, "or" is just like "and" with the implications turned around!
If you learn these patterns, you can learn to recognize products and coproducts when you see them... and you'll start seeing that math has far fewer truly distinct concepts that most people think!
Category theory makes you smarter by letting you 'compress' math.
December 13, 2019
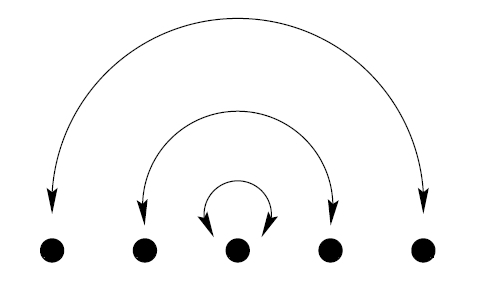
Is there a set with \(2\frac{1}{2}\) elements? No! But here you see a 'groupoid' with \(2\frac{1}{2}\) elements. To get it, just take a set with 5 elements and fold it in half. The point in the middle gets folded over, and becomes half a point.
Sounds wacky, but you can make this into rigorous math!
A groupoid has objects (points) and morphisms (arrows between points). We can 'compose' morphisms \(f \colon x \to y\) and \(g \colon y \to z\) and get a morphism \(gf \colon x \to z\). Composition is associative. Each object \(x\) has an identity for composition, \(1_x \colon x \to x \). Morphisms have inverses. That's all there is to it!
A set is the same as a groupoid with only identity morphisms. So, it has objects (points) but no interesting morphisms. A group is the same as a groupoid with just one object \(x\). The elements of our group are the morphisms \(f \colon x \to x\).
So you already know some groupoids.
Around 2000 I figured out how to define the cardinality of a groupoid.
For a groupoid that's just a set, the cardinality is just the number of objects. But throwing in extra morphisms reduces the cardinality!
If you have a group \(G\), you get a groupoid with one object: call it \(BG\). Elements of \(G\) give morphisms in \(BG\). The cardinality of \(BG\) is one over the usual cardinality of \(G\): $$ |BG| = 1/|G| $$ So, the more morphisms \(BG\) has, the smaller its cardinality gets!
Why should this be? It's because morphisms in a groupoid are 'ways for objects to be the same' (or more precisely, 'isomorphic'). If an object is the same as itself in a lot of ways, it acts smaller, as it it were 'folded over'.
That's the vague intuition, anyway.
It turns out that nature knows about this!
In particle physics, we compute the amplitude for particles to interact by summing over Feynman diagrams. But if a diagram has symmetries, we have to divide by the number of symmetries to get the right answer!

So there's not really a set of Feynman diagrams — there's a groupoid of them. And groupoid cardinality is not just crazy stuff made up by mathematicians. It's part of how nature works! For more, try:
In recent weeks I've learned something new about groupoid cardinality. I've been studying random structures in combinatorics. Like: if you have a random permutation of a 7-element set, how many cycles does it have, on average?
These averages are often fractions. For example, the answer to the question I just asked is \(363/140\).
And it turns out these numbers are sometimes groupoid cardinalities!
It should have been obvious, since when you average over permutations you divide by \(n!\), which is the number of elements of a permutation group. But now I see that some formulas for averages in combinatorics are secretly coming from equivalences between groupoids.
You see, in combinatorics there's an idea called 'bijective proof'. To prove an equation between natural numbers, like $$ \binom{n+1}{k} = \binom{n}{k} + \binom{n}{k-1} $$ you set up a 1-1 correspondence between finite sets.
But what about equations between fractions?
You can sometimes prove equations between fractions by setting up an equivalence between groupoids! Equivalent groupoids have the same cardinality.
So I've been doing this, and it's lots of fun:
For more, try Qiaochu Yuan's article on groupoid cardinality:
or this introduction:
Today we drove to Kingman, Arizona. After driving up the Cajon Pass we
had a late breakfast at Molly Brown's Country Cafe in Victorville. Then
we took a long drive through the Mojave Desert, full of yuccas and
volcanic
formations — only about 20,000 years ago, this area was
flowing with lava! We reached Kingman around 6:30 pm, and checked into
the Best Western Wayfarer's Inn.
December 15, 2019
Today we drove from Kingman to Flagstaff. It's a long and beautiful
gentle uphill drive into the colder altitudes of Arizona. Lisa looked
in her favorite Navajo jewelry store and I sat in the Marriott hotel
blogging about random permutations and other
math topics (moved to my December 12 and 13 diary entries).
Then we met in a cafe. There we had the lucky fortune to meet a woman
named Risha VanderWey, who is the superintendent of schools at the
Tuba City Unified School District. Tuba City is the main town in the
western side of the Navajo Nation... and Risha is in charge of a huge
area where Navajo and Hopi students may need to take 1½-hour
bus rides to school. It's a tough job: many of the students are very
poor and short of food, and lots of people in her employ don't even
show up to work half the time, but she can't fire them all because
there's not enough other people to hire to take their place! But she
seems really dedicated, energetic and nice. I hope to meet her in
Tuba City someday and see some schools.
December 16, 2019

On Monday we drove from Flagstaff to Cameron in order to stay at the Cameron Trading Post. This feels like the "last homely house" in Lord of the Rings — a cozy place to stay on the edge of the wilderness.

But en route, we took a little eastward detour and stopped by Wupatupqa, also known as Walnut Canyon National Monument. As you descend into this canyon you can see dozens of cliff dwellings, which were inhabited from 1100 to 1250 AD:

Zooming in on the same one:

Then, you can take a trail loop that lets you explore the ruins of some of the dwellings:


Here's another:

As you walk, you can continue to see other dwellings across the canyon:

The inhabitants made thorough use of local plants, especially the banana yucca:

All in all, a refreshing and inspiring afternoon!
December 17, 2019
On Tuesday I had my usual blue corn pancake for breakfast at the Cameron
Trading Post and Lisa bought an irresistible turquoise pendant.
We then drove from Cameron through Tuba City and southeast along Route 264 through the Navajo Nation and Hopi reservation. We tried to buy some blue corn flour from a mill run by an old woman in Hotevilla, which we've done before, but the mill was closed. We asked around at various stops, and it turns out that due to the drought the corn didn't grow well this year! So, we drove on.
In our search for blue corn flour and art we accidentally popped into a Hopi radio station, KUYI 88.1 FM. I'd seen a sign for an art gallery. As I pushed open the door I said "This is the wrong place", but someone inside said "This is the right place!" They were very friendly, and Lisa wound up doing an announcement for them!


We went on to visit the famous Hubbell Trading Post, which actually had blue corn flour for sale, as well as a striking rug, which was too expensive for us:

We made it to Gallup around 6 pm and pulled into the Best Western, right
behind the Hotel El Rancho on Route 66. El Rancho, while romantic,
is not very comfortable for a long stay.
December 20, 2019
As in the last two years, Lisa took weaving lessons in Gallup from
Gloria Begay at a store called Weaving in Beauty, owned by Mary
Walker. I spent a couple of days holed up blogging about random permutations.
On our last day there, Friday the 20th, we drove an hour north to see the Toadlena Trading Post. We'd been wanting to visit Two Grey Hills, since that town has given his name to a famous style of rug. But the trading post there was closed, and I'm now convinced that Toadlena was the better choice!



In Arizona and New Mexico, trading posts have long been the way the Hopi and Navajo buy from and sell to the European invaders. This particular one has an amazing collection of Navajo rugs, some for sale and others in a little museum section, unheated and ice-cold when Lisa and I visited.


The fellow who owns this place has written an amazingly detailed, lavishly illustrated 600-page book on the local weavers and their textiles. We bought a copy:
The store in the trading post is heated by a charming old stove that burns wood and coal:

After a spell in the museum we had to pop back to this stove to warm ourselves up! Then we went back to the museum... then back to the stove, etc.
The establishment was being run by a 68-year-old Navajo woman who had
been there for 14 years after spending most of her life in Denver.
She said she didn't speak much Navajo. We asked if she'd learned more
now that's she's back in New Mexico. She said she wanted to but
didn't have much time to study it. She said life was much busier out
in the country: growing crops, minding the store, etc. I found that
interesting.
December 22, 2019
Yesterday, Saturday, we drove back starting at noon. We spent a night
in Prescott, Arizona and had a fun dinner at The Palace, a historic
saloon with surprisingly good food. After a hard day's driving we got
back Sunday night — after a short stop in La Quinta to visit
some friends and eat some mince pie!
December 25, 2019

Schrödinger and Einstein helped invent quantum mechanics, but they didn't really believe in its implications for the structure of reality, so they couldn't get themselves to work on it. Thus, they were sidelined for the rest of their careers. While others made rapid progress in nuclear physics, particle physics and quantum field theory, they criticized quantum theory and tried to invent 'unified field theories'.
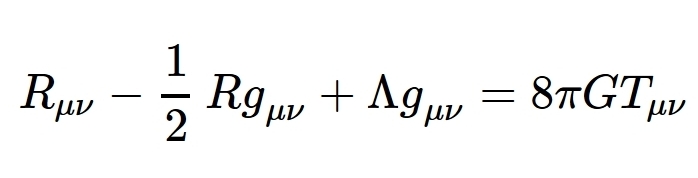
After he finally found his equations describing gravity in November 1915, Einstein spent years working out their consequences. In 1917 he changed the equations, introducing the 'cosmological constant' \(\Lambda\) to keep the universe from expanding. Whoops.

In 1923, Einstein got excited about attempts to unify gravity and electromagnetism. He wrote to Niels Bohr:
I believe I have finally understood the connection between electricity and gravitation. Eddington has come closer to the truth than Weyl.You see, Hermann Weyl and Arthur Eddington had both tried to develop unified field theories — theories that unified gravity and electromagnetism. Weyl had tried a gauge theory — indeed, he invented the term 'gauge transformations' at this time. In 1918 he asked Einstein to communicate a paper on it to the Berlin Academy. Einstein did, but pointed out a crushing physical objection to it in a footnote!
In 1921, Eddington tried a theory where the fundamental field was not the spacetime metric, but a torsion-free connection. He tried to show that both electromagnetism and gravity could be described by such a theory. But he didn't even get as far as writing down field equations.
Einstein wrote three papers on Eddington's ideas in 1923. He was so excited that he sent the first to the Berlin Academy from a ship sailing from Japan! He wrote down field equations and sought to connect them to Maxwell's equations and general relativity. He was very optimistic at this time, concluding that
Eddington's general idea in context with the Hamiltonian principle leads to a theory almost free of ambiguities; it does justice to our present knowledge about gravitation and electricity and unifies both kinds of fields in a truly accomplished manner.
Later he noticed the flaws in the theory. He had an elaborate approach to getting charged particles from singular solutions of the equation, though he wished they could be described by nonsingular solutions. He was stumped by the fact that the negatively and positively charged particles he knew — the electron and positron — had different masses. The same problem afflicted Dirac later, until the positron was discovered. But there were also problems even in getting Maxwell's equations and general relativity from this framework, even approximately.
By the 1925 his enthusiasm had faded. He wrote to his friend Besso:
Regrettably, I had to throw away my work in the spirit of Eddington. Anyway, I now am convinced that, unfortunately, nothing can be made with the complex of ideas by Weyl–Eddington.So, he started work on another unified field theory. And another. And another.
Einstein worked obsessively on unified field theories until his death in 1955. He lost touch with his colleagues' discoveries in particle physics. He had an assistant, Valentine Bargmann, try to teach him quantum field theory — but he lost interest in a month. All he wanted was a geometrical explanation of gravity and electromagnetism. He never succeeded in this quest.

But there's more to this story!
The other side of the story is Schrödinger. In the 1940s, he too became obsessed with unified field theories. He and Einstein became good friends — but also competitors in their quest to unify the forces of nature.

I think I'll tell the rest of this story later! For more technical details, try these excellent papers:
I am very happy that in the paper just published in P.R. you have evidently caught dogmatic q.m. by the coat-tails.Einstein replied:
You are the only person with whom I am actually willing to come to terms.They bonded over their philosophical opposition to the Bohr–Heisenberg attitude to quantum mechanics. In November 1935, Schrödinger wrote his paper on 'Schrödinger's cat'.
Schrödinger fled Austria after the Nazis took over. In 1940 he got a job at the brand-new Dublin Institute for Advanced Studies.
In 1943 he started writing about unified field theories, corresponding with Einstein. He worked on some theories very similar to those of Einstein and Straus, who were trying to unify gravity and electromagnetism in a theory involving a connection with torsion, whose Levi-Civita symbol was therefore non-symmetric. He wrote 8 papers on this subject.
Einstein even sent Schrödinger two of his unpublished papers on these ideas!

In late 1946, Schrödinger had a new insight. He was thrilled.

By 1947 Schrödinger thought he'd made a breakthrough. He presented a paper on January 27th at the Dublin Institute of Advanced Studies. He even called a press conference to announce his new theory!
He predicted that a rotating mass would generate a magnetic field.

The story of the great discovery was quickly telegraphed around the world, and the science editor of the New York Times interview Einstein to see what he thought.
Einstein was not impressed. In a carefully prepared statement he shot Schrödinger down:

Einstein was especially annoyed that Schrödinger had called a press conference to announce his new theory before there was any evidence supporting it.

Wise words. I wish people heeded them!
Schrödinger apologized in a letter to Einstein, claiming that he'd done the press conference just to get a pay raise. Einstein responded curtly, saying "your theory does not really differ from mine".
They stopped writing to each other for 3 years.


I'd like to understand Schrödinger's theory using the modern tools of differential geometry. I don't think it's promising. I just want to know what it actually predicts! Go here for details: