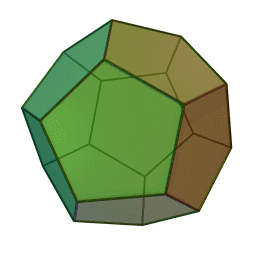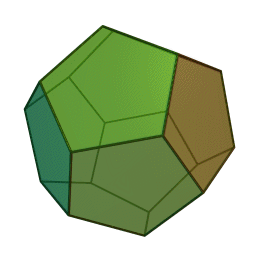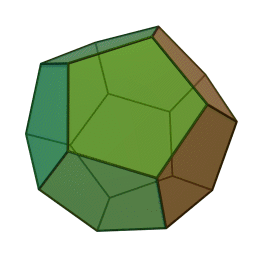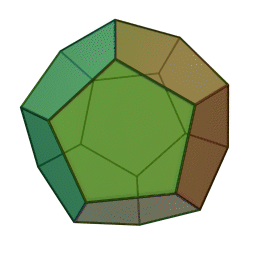
My favorite Platonic solids are the regular dodecahedron, with 12 faces and 20 corners:
and the regular icosahedron, with 12 corners and 20 faces:
They are close relatives, with all the same symmetries... but what excites me most is that they have 5-fold symmetry. It's a theorem that no crystal can have that kind of symmetry. So, we might wonder whether these shapes occur in nature... and if they don't, how people dreamt up these shapes in the first place.
It's widely believed that the Pythagoreans dreamt up the regular dodecahedron after seeing crystals of iron pyrite—the mineral also known as 'fool's gold'. Nobody has any proof of this. However, there were a lot of Pythagoreans in Sicily back around 500 BC, and also a lot of pyrite. And, it's fairly common for pyrite to form crystals like this:
This crystal is a 'pyritohedron'. It looks similar to regular dodecahedron—but it's not! At the molecular level, iron pyrite has little cubic crystal cells. But these cubes can form a pyritohedron:
(By the way, you can click on any of these pictures for more information.)
You'll notice that the front face of this pyritohedron is like a staircase with steps that go up 2 cubes for each step forwards. In other words, a staircase with slope 2. That's the key to the math here! By definition, the pyritohedron has faces formed by planes at right angles to these 12 vectors:
$$ \begin{array}{cccc} (2,1,0) & (2,-1,0) & (-2,1,0) & (-2,-1,0) \\ (1,0,2) & (-1,0,2) & (1,0,-2) & (-1,0,-2) \\ (0,2,1) & (0,2,-1) & (0,-2,1) & (0,-2,-1) \\ \end{array} $$
On the other hand, a regular dodecahedron has faces formed by planes at right angles to some very similar vectors, where the number 2 has been replaced by this number, called the golden ratio:
\[ \displaystyle {\Phi = \frac{\sqrt{5} + 1}{2}} \]
Namely, these vectors:
$$ \begin{array}{cccc} (\Phi,1,0) & (\Phi,-1,0) & (-\Phi,1,0) & (-\Phi,-1,0) \\ (1,0,\Phi) & (-1,0,\Phi) & (1,0,-\Phi) & (-1,0,-\Phi) \\ (0,\Phi,1) & (0,\Phi,-1) & (0,-\Phi,1) & (0,-\Phi,-1) \\ \end{array} $$
Since
\[ \Phi \approx 1.618... \]
the golden ratio is not terribly far from 2. So, the pyritohedron is a passable attempt at a regular dodecahedron. Perhaps it was even good enough to trick the Pythagoreans into inventing the real thing.
If so, we can say: fool's gold made a fool's golden ratio good enough to fool the Greeks.
At this point I can't resist a digression. You get the Fibonacci numbers by starting with two 1's and then generating a list of numbers where each is the sum of the previous two:
\[ 1, 1, 2, 3, 5, 8, 13, ... \]
The ratios of consecutive Fibonacci numbers get closer and closer to the golden ratio. For example:
\[ \begin{array}{ccl} 2/1 &=& 1 \\ 2/1 &=& 2 \\ 3/2 &=& 1.5 \\ 5/3 &=& 1.666... \\ 8/5 &=& 1.6 \\ \end{array} \]
and so on. So, in theory, we could use these ratios to make cubical crystals that come closer and closer to a regular dodecahedron!
And in fact, pyrite doesn't just form the 2/1 pyritohedron I showed you earlier. Sometimes it forms a 3/2 pyritohedron! This is noticeably better. The 2/1 version looks like this:
while the 3/2 version looks like this:
Okay. End of digression. But there's another trick we can play!
These 12 vectors I mentioned:
$$ \begin{array}{cccc} (2,1,0) & (2,-1,0) & (-2,1,0) & (-2,-1,0) \\ (1,0,2) & (-1,0,2) & (1,0,-2) & (-1,0,-2) \\ (0,2,1) & (0,2,-1) & (0,-2,1) & (0,-2,-1) \\ \end{array} $$
besides being at right angles to the faces of the dodecahedron, are also the corners of the icosahedron!
And if we use the number 2 here instead of the number \(\Phi\), we get the vertices of a so-called pseudoicosahedron. Again, this can be made out of cubes:
However, nobody seems to think the Greeks ever saw a crystal shaped like a pseudoicosahedron! The icosahedron is first mentioned in Book XIII of Euclid's Elements, which speaks of:
the five so-called Platonic figures which, however, do not belong to Plato, three of the five being due to the Pythagoreans, namely the cube, the pyramid, and the dodecahedron, while the octahedron and the icosahedron are due to Theaetetus.
So, maybe Theaetetus discovered the icosahedron. Indeed, Benno Artmann has argued that this shape was the first mathematical object that was a pure creation of human thought, not inspired by anything people saw!
That idea is controversial. It leads to some fascinating puzzles, like: did the Scots make stone balls shaped like Platonic solids back in 2000 BC? For more on these puzzles, try this:
• John Baez, Who discovered the icosahedron?
But right now I want to head in another direction. It turns out iron pyrite can form a crystal shaped like a pseudoicosahedron! And as Johan Kjellman pointed out to me, one of these crystals was recently auctioned off... for only 47 dollars!
It's beautiful:
So: did the Greeks ever seen one of these? Alas, we may never know.
For more on these ideas, see:
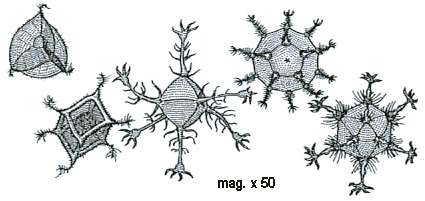
To wrap up, I should admit that icosahedra and dodecahedra show up in many other places in nature—but probably too small for the ancient Greeks to see. Here are some sea creatures magnified 50 times:
And here's a virus containing a dodecahedral cage of double-stranded RNA:
The gray bar on top is 10 nanometers long, while the bar on bottom is just 5 nanometers long.
The mathematics of viruses with 5-fold symmetry is fascinating. Just today, I learned of Reidun Twarock's recent discoveries in this area:
Most viruses with 5-fold symmetry have protein shells in patterns based on the same math as geodesic domes:
But some more unusual viruses, like polyomavirus and simian virus 40, use more sophisticated patterns made of two kinds of tiles:
They still have 5-fold symmetry, but these patterns are spherical versions of Penrose tilings! A Penrose tiling is a nonrepeating pattern on the plane, typically with approximate 5-fold symmetry, made out of two kinds of tiles:
To understand these more unusual viruses, Twarock needed to use some very clever math:
But that's another story for another day!
