John Baez
Spans and the Categorified Heisenberg Algebra
Heisenberg reinvented matrices while discovering quantum mechanics,
and the algebra generated by annihilation and creation operators
obeying the canonical commutation relations was named after him. It
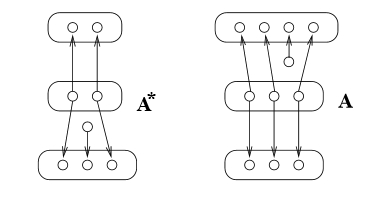
turns out that matrices arise naturally from 'spans', where a span
between two objects is just a third object with maps to both those
two. In terms of spans, the canonical commutation relations have a
simple combinatorial interpretation.
More recently, Khovanov introduced a
'categorified' Heisenberg algebra, where the canonical commutation
relations hold only up to isomorphism, and these isomorphisms obey new
relations of their own. The categorified
Heisenberg algebra naturally acts on the '2-Fock space' describing
collections of particles in a 4-dimensional topological quantum field
theory.
The meaning of the new relations in the categorified Heisenberg
algebra was initially rather mysterious. However, Jeffrey Morton and Jamie Vicary
have shown that they again have a nice interpretation in terms of
spans. We can begin to formalize this using the work of Alex Hoffnung and Mike Stay, who have shown that
spans of groupoids are morphisms in a symmetric monoidal bicategory.
I gave a talk on this at Oxford and Université Paris 7,
and a 3-hour minicourse on it in Lanzhou. Here's the talk:
-
Spans and the Categorified Heisenberg Algebra: slides
and video.
The minicourse goes into more detail; you can see the slides here:
-
Part 1 – How
Jeffrey Morton and Jamie
Vicary categorified the Heisenberg algebra using spans of groupoids.
-
Part 2 –
The definition of symmetric monoidal
bicategory, following Mike Stay.
-
Part 3 –
How the categorified Heisenberg algebra manifests in linear
algebra and the theory of Young diagrams.
For more on this subject try these papers:
-
Mikhail Khovanov, Heisenberg algebra and a graphical calculus.
-
Jeffrey Morton and Jamie Vicary, The categorified Heisenberg algebra
I: a combinatorial representation.
-
Jeffrey Morton, 2-Vector
spaces and groupoids.
-
Jeffrey Morton, Categorified algebra and
quantum mechanics.
-
Alex Hoffnung, Spans in
2-categories: a monoidal tricategory.
- Mike Stay, Compact closed
bicategories.
-
John Baez and James Dolan, From finite sets to Feynman
diagrams.
-
John Baez and James Dolan,
Higher-dimensional algebra
and topological quantum field theory.
-
John Baez,
Higher-dimensional algebra
I: 2-Hilbert spaces.
-
John Baez, Alex Hoffnung and Christopher Walker, Higher-dimensional algebra VII:
groupoidification.
For more on the idea of using spans in quantum mechanics,
try this talk of mine:
Text © 2013 John Baez
Creation and annihilation spans by Jeffrey Morton,
truncated shuffle polytope by Mike Stay,
Young diagrams by Jeffrey Morton and Jamie Vicary
baez@math.removethis.ucr.andthis.edu