




|
 
|

|
Today I'd like to talk a bit about the first stars in the Universe, and some hotly contested possible observations of these stars. Then I want to describe a new paper by my student Derek Wise. But first - if anyone gave you a gift certificate for a bookstore this holiday season, here are two suggestions.
The first one is really easy and fun:
1) William Poundstone, Fortune's Formula: The Untold Story of the Scientific Betting System that Beat the Casinos and Wall Street, Farrar, Strauss and Giroux, New York, 2005.
Packed with rollicking tales of gangsters, horse-racing, blackjack, and insider trading, this is secretly the story of how Claude Shannon developed information theory - and how he and his sidekick John Kelly Jr. used it to make money in casinos and Wall Street. I'd known about Shannon's work on information... but not that he beat 99.9% of mutual fund managers, making an average compound return of 28% for many years - as compared to 27% for Warren Buffett!
This book has just a few equations in it. I was delighted by one discovered by Kelly, which I'd never seen before. Translating into my own favorite notation, it goes like this:
S = log M
It's the fundamental equation relating gambling to information! Let me explain it - in language far more complicated than you'll see in Poundstone's book.
What's M? It's the best possible average growth of a gambler's money. For example, if his best possible strategy lets him triple his money on average, then M = 3.
What's S? This is the amount of "inside information" the gambler has: information he has, that the people he's betting against don't.
Some technical stuff: First, the above "average" is a geometric mean, not an arithmetic mean. Second, if we measure information in bits, we need to use base 2 in the logarithm. Physicists would probably prefer to use base e, which means measuring information in "nits". It doesn't really matter, but let's use base 2 for now.
To get a feeling for why Kelly's theorem is true, it's best to start with the simplest example. If S = 1, then M = 2. So, if a gambler receives one bit of inside information, he can double his money!
This sounds amazing, but it's also obvious.
Suppose you have one bit of inside information: for example, whether a flipped coin will land heads up or tails up. Then you can make a bet with somebody where they give you $1,000,000 if you guess the coin flip correctly, and you give them $1,000,000 if you guess wrong. This is a fair bet, so they will accept. That is, they'll think it's fair if they don't suspect you have inside information! But since you do have this information, you'll win the bet, and double your money on this coin flip.
Kelly's equation is usually phrased in terms of the rate at which the gambler gets inside information, and the rate at which his money grows. So, for example, to earn 12% interest annually, you only need to receive
log(1.12) = 0.163
bits of inside information - and find some dupe willing to make bets with you about this.
The last part is the hard part: the "inside information" really needs to be information people don't believe you have. I must learn hundreds of bits of information about math each year - stuff only I know - but I haven't found anyone simultaneously smart enough to understand it and dumb enough to make bets with me about it!
Still, I like this relation between information theory and gambling, because one stream of Bayesian probability theory says probabilities are subjectively defined in terms of the bets you would accept.
The argument for this is called the "Dutch book argument". It basically shows how you can make money off someone who makes bets in ways that correspond to stupid probabilities that don't add to 1, or fail to be coherent in other ways:
2) Carlton M. Caves, Probabilities as betting odds and the Dutch book, available at http://info.phys.unm.edu/~caves/reports/dutchbook.pdf
So, there's a deep relation between gambling and probability - no news here, really.
But, there's also a deep relation between probability and information theory, discovered by Shannon. Briefly, it goes like this: the information you obtain by learning the value of a random variable is
S = - ∑ i pi log(pi)
where the sum is taken over all the possible values of this random variable, and pi is the probability that it takes its ith value. So, for example, if you flip a fair coin, where p1 = p2 = 1/2, the information you get by looking at the coin is
-[1/2 log(1/2) + 1/2 log(1/2)] = 1
One bit!
So: gambling is related to probability, and probability is related to information. Kelly's result closes the circle by providing a direct relation between gambling and information!
But, apparently some of Kelly's ideas are still controversial in the world of economics and stock trading. If you read Poundstone's book, you'll learn why.
The next book takes more persistence to read:
3) Avner Ash and Robert Gross, Fearless Symmetry: Exposing the Hidden Patterns of Numbers, Princeton U. Press, Princeton, 2006.
The authors do a creditable job of what might at first seem utterly impossible: explaining heavy-duty modern number theory to ordinary mortals. The formal prerequisites are little more than high school algebra, and the style is expository, but anyone except an expert will need to stop and think at times.
They start by explaining modular arithmetic - you know, stuff like adding and multiplying "mod 7". Then they tackle groups, and permutations, since the main theme of the book is symmetry. Then they move on to algebraic varieties, in a simple no-nonsense style cleverly adapted from Grothendieck's later work (without terrifying the reader by mentioning this fact).
Next they tackle some serious number theory: quadratic reciprocity, Galois groups, and elliptic curves. Then they describe more general forms of reciprocity, leading up to a taste of the Langlands program. They conclude with a sketch of how Fermat's last theorem was proved.
These days mathematical physicists are all excited about a variant of the Langlands program: the so-called "geometric" Langlands program, which is related to string theory. Drinfeld has been running a seminar on this at Chicago for years, but that's not what got the physicists interested - it's these papers by Witten that did it:
4) Anton Kapustin and Edward Witten, Electric-magnetic duality and the geometric Langlands program, 225 pages, available as hep-th/0604151.
5) Sergei Gukov and Edward Witten, Gauge theory, ramification, and the geometric Langlands program, 160 pages, available as hep-th/0612073.
So, if you're trying to learn this geometric Langlands stuff, and you want to fit it into the grand landscape of mathematics, the book Fearless Symmetry could be a fun way to learn some the math underlying the ordinary Langlands stuff.
I started girding myself for a discussion of the Langlands program in "week217", "week218" and "week221", but then I got distracted. I'll get back to it someday, but right now I'm in the mood for lighter stuff... so let me tell you a bit about the first stars.
The story starts around 380,000 years after the Big Bang, when the hot hydrogen and helium forming our Universe cooled down to 3000 kelvin - just cool enough for the electrons to stick to the atomic nuclei instead of zipping around on their own.
When the electrons in a gas are hot enough for some to zip around on their own, we say the gas is "ionized". When a lot of them are zipping around, we call it a "plasma". Because charged particles interact with the electromagnetic field, light doesn't pass through plasma cleanly: it keeps getting absorbed and re-emitted.
So, before our story started, you couldn't see very far: it would be like trying to look through a wall of fire. But, around 380,000 years after the Big Bang, the gas became transparent!
What would it have looked like? Nobody ever seems to talk about this. So, I'll just guess, and hope some expert corrects me.
Back when the gas filling the Universe was 5000 kelvin in temperature, just a bit cooler than the surface of the Sun, everything was yellow. You couldn't see far at all: you would have been blinded by a yellow glare.
But when it cooled to 4000 kelvin in temperature, the Universe became orange.
And when it cooled to 3000 kelvin, the Universe became red.
And when it cooled a tiny bit further, it became infrared. As far as visible light goes, the Universe became transparent!
This would happen everywhere more or less at once. But since light takes time to travel, you'd see a transparent sphere around you, expanding outwards at the speed of light, with reddish walls.
It's been sort of like this ever since.
So, when we look far away with our best telescopes, we look back in time to the time when the Universe became transparent - but no further. We're surrounded by a distant, ancient wall of fire. It's now about 13.3 billion light-years away - or 13.3 billion year back in time, if you prefer. And, it's receding at a rate of one light-year per year.
But by now, the light from this wall of fire has been severely redshifted. In other words, it's been stretched along with the expansion of the Universe - stretched by a factor of 1100, in fact!
So, what had been the hot infrared glow of 3000-kelvin plasma is now a feeble microwave glow corresponding to an icy temperature of 2.7 kelvin. This is the famous "cosmic microwave background radiation".
But let's go back in time....
From the moment the hot gas became transparent to the time when the first stars formed, the Universe was dark except for the dimming infrared glow of that distant wall of fire. This era is called the "Dark Ages".
During the Dark Ages, gas cooled down and clumped under its own gravity - apparently with a lot of help from cold dark matter of some unknown sort. Without postulating this matter, nobody can figure out how galaxies formed as soon as they did.
As befits their name, the Dark Ages are still shrouded in mystery. There are a lot of unanswered questions besides the nature of dark matter. Which formed first - individual stars, or galaxies? And, when did the Dark Ages end?
It's currently believed that the first stars formed sometime between 150 million and 1 billion years after the Big Bang.
At the later end of that range, the Universe could have gotten quite cold before starlight warmed up the interstellar gas and reionized it. There's even a spooky theory that the Universe was full of hydrogen snowflakes near the end of the Dark Ages - see "week196" for more on this, and a timeline of the earlier history of the Universe.
But, the current best guess, based on data from the Wilkinson Microwave Anisotopy Probe, says that reionization happened 400 million years after the Big Bang:
6) Marcelo A. Alvarez, Paul R. Shapiro, Kyungjin Ahn and Ilian T. Iliev, Implications of WMAP 3 year data for the sources of reionization, Astrophys. J. 644 (2006), L101-L104. Also available as astro-ph/0604447.
This would be too early for hydrogen snow, since my rough calculation says the microwave background radiation was 30 kelvin then, while hydrogen freezes at 14 kelvin.
What were the first stars like? Without heavier elements to catalyze nuclear fusion, they could have been larger than current-day stars: perhaps hundreds of times the size of our Sun! These so-called Population III stars have not actually been seen. But, it's possible that we've finally caught a glimpse of them, not individually but in a sort of statistical sense:
7) A. Kashlinsky, R. G. Arendt, J. Mather and S. H. Moseley, New measurements of cosmic infrared background fluctuations from early epochs, to appear in Ap. J. Letters. Available as astro-ph/0612445.
8) A. Kashlinsky, R. G. Arendt, J. Mather and S. H. Moseley, On the nature of the sources of the cosmic infrared background, to appear in Ap. J. Letters. Available as astro-ph/0612447.
Using delicate techniques to carefully sift through the infrared (not microwave) background radiation, the authors claim to find radiation not accounted for by previously known sources. Assuming the standard cosmological scenario, the sources of this radiation date back to less than 1 billion years after the Big Bang, and were individually much brighter than current-day stars.
Here's a picture of their data:
9) NASA / JPL-Caltech / A. Kashlinsky, Infrared background light from first stars, http://www.spitzer.caltech.edu/Media/releases/ssc2005-22/
On top is a photograph taken by the Spitzer Space Telescope: a 10-hour infrared exposure of a tiny patch of sky, 6 × 12 arcminutes across, chosen for having a bare minimum of foreground stars, galaxies and dust. (For comparison, the Moon is 30 arcminutes across.) On the bottom is the same picture with known sources of infrared subtracted. What's left may be the severely redshifted light from early stars!
Or, it may not. In the following news story, Ned Wright of UCLA said, "I'm very skeptical of this result. I think it's wrong. I think what they're seeing is incompletely subtracted residuals from nearby sources."
10) Dinesh Ramde, Associated Press, Hints of early stars may have been found, http://www.usatoday.com/tech/science/space/2005-11-02-early-stars_x.htm
So, we'll have to see how it goes....
But in the meantime, we can think about mathematical physics. My student Derek Wise is graduating this year, and he's doing his thesis on Cartan geometry, MacDowell-Mansouri gravity and BF theory. Let me say a little about this paper of his:
11) Derek Wise, MacDowell-Mansouri gravity and Cartan geometry, available as gr-qc/0611154.
Elie Cartan is one of the most influential of 20th-century geometers. At one point he had an intense correspondence with Einstein on general relativity. His "Cartan geometry" idea is an approach to the concept of parallel transport that predates the widely used Ehresmann approach (connections on principal bundles). It simultaneously generalizes Riemannian geometry and Klein's Erlangen program (see "week213"), in which geometries are described by their symmetry groups:
EUCLIDEAN GEOMETRY -------------> KLEIN GEOMETRY
| |
| |
| |
| |
v v
RIEMANNIAN GEOMETRY --------------> CARTAN GEOMETRY
Given all this, it's somewhat surprising how few physicists know
about Cartan geometry!
Recognizing this, Derek explains Cartan geometry from scratch before showing how it underlies the so-called MacDowell-Mansouri approach to general relativity. This plays an important role both in supergravity and Freidel and Starodubtsev's work on quantum gravity (see "week235") - but until now, it's always seemed like a "trick".
What's the basic idea? Derek explains it all very clearly, so I'll just provide a quick sketch. Cartan describes the geometry of a lumpy bumpy space by saying what it would be like to roll a nice homogeneous "model space" on it. Homogeneous spaces are what Klein studied; now Cartan takes this idea and runs with it... or maybe we should say he rolls with it!
For example, we could study the geometry of a lumpy bumpy surface by rolling a plane on it. If our surface is itself a plane, this rolling motion is trivial, and we say the surface is "flat" in the sense of Cartan geometry. But in general, the rolling motion is interesting and serves to probe the geometry of the surface.
Alternatively, we could study the geometry of the same surface by rolling a sphere on it. Derek illustrates this with a picture of a hamster crawling around in a plastic "hamster ball", which is something you can actually buy for your pet hamster to let it explore your house without escaping or getting in trouble:
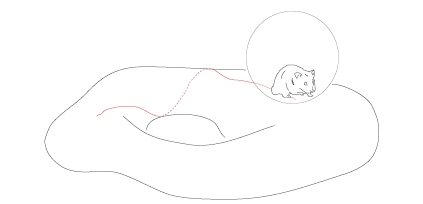
(I've read about falling cats in papers on gauge theory, but this is the first mathematical physics paper I've read containing the word "hamster".)
If our surface is itself a sphere of the same radius, this rolling motion is trivial, and we say the surface is flat in the sense of Cartan geometry - but now it's a different sense than when we used a plane as our "model geometry"!
Which model geometry should we use in a given problem? It depends on which one best approximates the lumpy bumpy space we're studying!
The ordinary formulation of general relativity fits into this framework, with a little work. Two well-known mathematical gadgets called the "Lorentz connection" and "coframe field" fit together to describe what would happen if we rolled a copy of Minkowski spacetime over the lumpy bumpy spacetime we live in.
That's great if Minkowski spacetime is the best homogeneous approximation to the spacetime we live in. But nowadays we think the cosmological constant is nonzero, so the Universe is expanding in a roughly exponential way. This makes another model geometry, "deSitter spacetime", the best one to use!
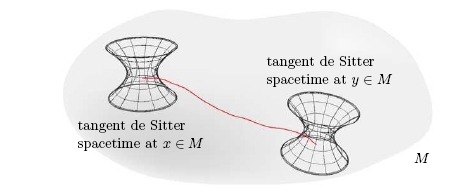
So, if we know Cartan geometry, we can use that... and we get something called the MacDowell-Mansouri formulation of gravity. Or, if we don't want our spacetime to have lumps and bumps - if we want it to look locally just like the Klein model geometry - we can use a different theory, a topological field theory called BF theory (see "week232").
In short, the passage from a topological field theory describing a "locally homogeneous" spacetime to full-fledged gravity with all its lumps and bumps is nicely understood in terms of how Cartan's approach to geometry generalizes Klein's!
For more details, you'll just have to read Derek's paper. You might also try these:
12) Michel Biesunski, Inside the coconut: the Einstein-Cartan discussion on distant parallelism, in Einstein and the History of General Relativity, eds. D. Howard and J. Stachel, Birkhauser, Boston, 1989.
This describes the correspondence between Cartan and Einstein. I believe this centered, not on Cartan geometry per se, but on the "teleparallel" formulation of gravity (see "week176"). But, they're somewhat related.
13) Richard W. Sharpe, Differential Geometry: Cartan's Generalization of Klein's Erlangen Program, Springer-Verlag, New York, 1997.
This is the main textbook on Cartan geometry. But, it's probably best to read a few chapters of Derek's paper first, since the key ideas are presented more intuitively.
My friend the geometer and analyst Rafe Mazzeo, whom I recently saw at Stanford, told me that Cartan geometry was all the rage these days. I'm embarrassed to say I hadn't known this! I think the kinds of Cartan geometry being intensively studied are related to conformal geometry, CR structures and stuff like that...
Merry Christmas!
Addenda: I thank Chris Weed for catching typos. For more discussion, go to the n-Category Café.
© 2006 John Baez
baez@math.removethis.ucr.andthis.edu

|
 
|

|