You can see the slides for all these talks here, and videos too.
Here are some kinds of networks I discuss:




You can also see the slides of this talk.
Click on any picture in the slides, or any text in blue, and get more
information!
To read more about the network theory project, go here:
You can also see the slides of this talk.
Click on any picture in the slides, or any text in blue, and get more
information!
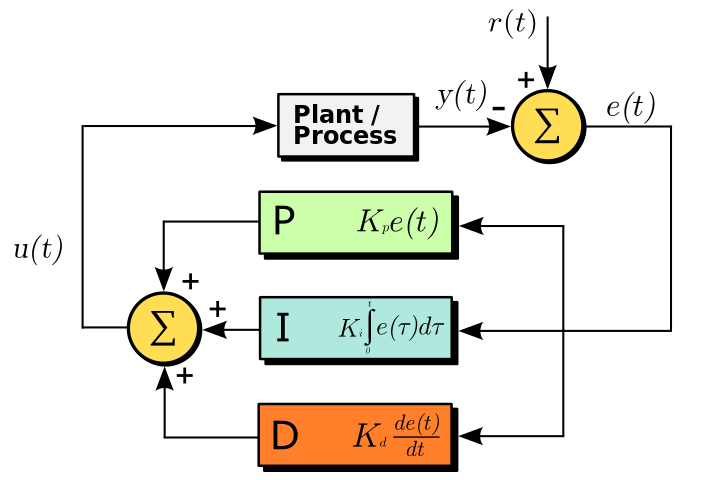
For more details on signal-flow graphs and control theory, see:
You can also see the slides of this talk.
Click on any picture in the slides, or any text in blue, and get more
information!
For more details, try this free book:
You can also see the slides of this talk.
Click on any picture in the slides, or any text in blue, and get more
information!
For more details on entropy and information, try:
For something a bit lighter, try these blog articles:
In my talk I mistakenly said that relative entropy is a continuous
functor; in fact it's just lower semicontinuous. I have fixed my slides.
The third part of my talk was my own interpretation of Brendan Fong's
master's thesis:
By making this slight change, I am claiming that causal theories can
be seen as algebraic
theories in the sense of Lawvere, and this would be a very good
thing, since we know a lot about those.
Overview
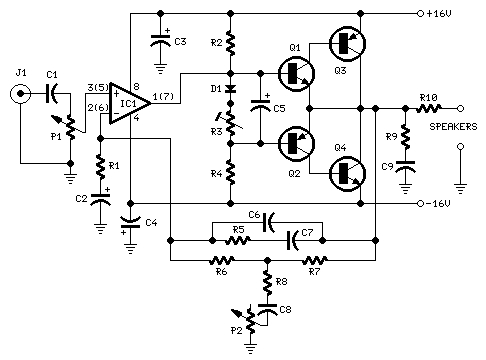
I. Electrical circuits and signal-flow graphs
For more on circuit diagrams, see:
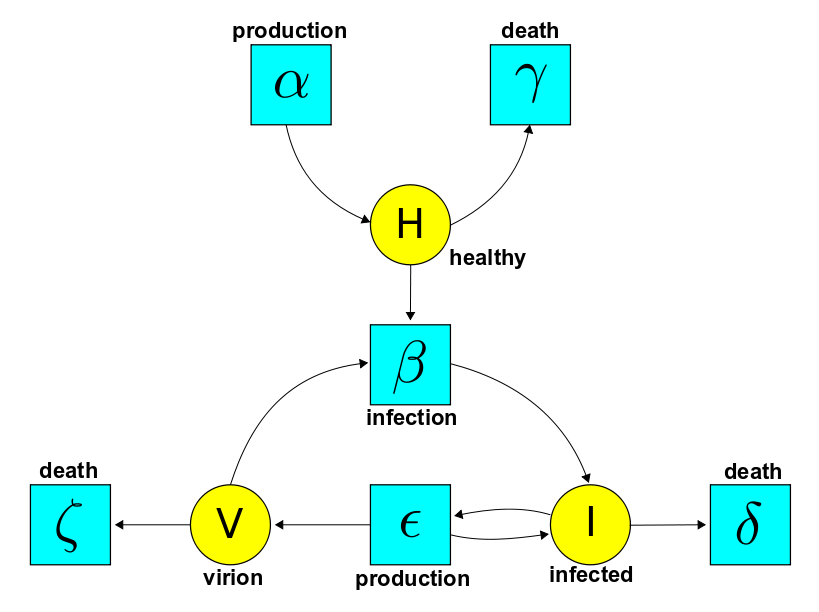
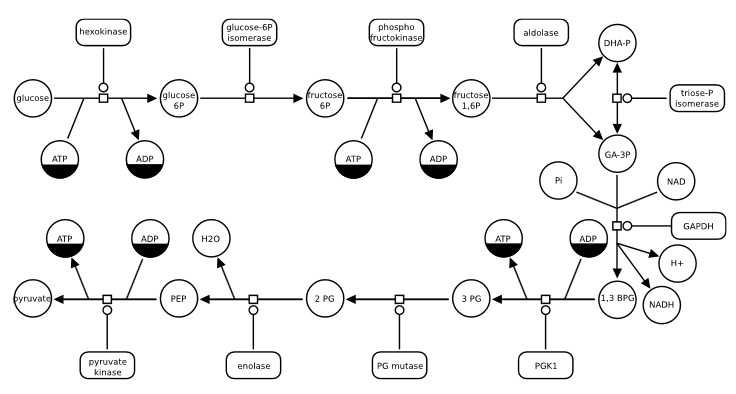
II. Stochastic Petri nets, chemical reaction networks and Feynman
diagrams
as well as this paper on the Anderson–Craciun–Kurtz theorem (discussed in my talk):
III. Entropy, information and Bayesian networks
© 2014 John Baez (except for images)
baez@math.removethis.ucr.andthis.edu
home