




|
 
|

|
This week I'd like to finish my news report from the Corfu summer school on quantum gravity. You'll hear how strings meet loops in BF theory, and how the Poincaré 2-group gives a spin foam model that mimics flat Minkowski spacetime.
But first: Timurid tiling patterns with 5-fold and 10-fold quasisymmetry, and the astronomy pictures of the week!
If you listen to the news, you probably heard that NASA discovered an enormous diffuse ring around Saturn. They did it using the Spitzer Space Telescope, a satellite equipped with a telescope that detects infrared light. In "week243" I showed you infrared light from the first stars in the Universe, and in "week257" I talked about magnesium and iron oxide dust emanating from the Red Rectangle. Both of those were discovered using the Spitzer.
Here's what the new ring would look like if you could see it:
1) Jet Propulsion Laboratory, NASA space telescope discovers largest ring around Saturn, October 6, 2009, http://www.jpl.nasa.gov/news/news.cfm?release=2009-150
As you probably heard, it dwarfs all the visible rings, and it's tilted relative to them. But even cooler is what the Spitzer Space Telescope actually saw:
2) NASA, Big band of dust, http://www.nasa.gov/mission_pages/spitzer/multimedia/spitzer-20091007d.html
It's an edge-on view of the new ring. It's fat: 20 Saturns thick. And if you look carefully, you'll see that it has two layers, with a bit of a gap in the middle. According to the scientists who discovered it, this is consistent with its origin:
3) Anne Verbiscer, Michael Skrutskie, and Doug Hamilton, Saturn's largest ring, Nature, October 7, 2009.
The point is that this ring surrounds the orbit of Saturn's moon Phoebe - a meteor-scarred hulk 100 kilometers across. While Phoebe looks like an asteroid, it's probably an interloper from the outer Solar System, because it's made of ice... but it's covered with a layer of dark material.
The newly discovered ring seems to be made of this dark stuff, blasted away from Phoebe by meteorite collisions. And its discoverers say the double-layered structure is characteristic of rings formed this way from moons with inclined orbits. (Jupiter also has some faint rings like this, poetically known as the "gossamer rings".)
What's really exciting about this new ring is that it explains one of the big mysteries of the Solar System: the dark spot on Saturn's moon Iapetus!
Iapetus is mostly icy, but one side is covered with dark stuff... probably cyanides and carbon-rich minerals. Now it seems this stuff was picked up from the newly discovered ring! It seems to have landed in lumps - mainly on the leading side of Iapetus. You see, this moon is locked in synchronous rotation with Saturn, just like our Moon always shows the same face to Earth. So, one side plows through space and picks up debris, while the other stays clean.
Here's a closeup of some lumps of dark stuff on Iapetus, taken by the Cassini probe:
4) NASA Photojournal, Spotty Iapetus, http://photojournal.jpl.nasa.gov/catalog/PIA08382
NASA Photojournal, Inky stains on a frozen moon, http://photojournal.jpl.nasa.gov/catalog/PIA08374
As you can see, in this region of Iapetus the dark stuff is found at the bottoms of craters. It could have formed these craters by impact, but its presence could also gradually make these craters deeper: the dark stuff should absors more sunlight and warm the nearby ice, making it "sublimate": that is, turn into water vapor.
Because it's locked in synchronous rotation with Saturn, the "day" on Iapetus is equal to one period of rotation, namely 79 of our Earth days. So, it's probably the warmest place in the Saturnian system during the daytime. Not very warm: just 113 kelvin on the ice. That's -160 °C! But in the dark regions it should be about 138 kelvin. This extra warmth should make more ice sublimate, making them even darker. It's been estimated that over one billion years the very dark regions would lose about 20 meters of ice to sublimation, while the light-colored regions would lose only 10 centimeters, not even counting the ice transferred from the dark regions.
If you want more, there's a great introduction to Saturn's rings in this blog, followed by a nontechnical summary of the new paper on the Phoebe ring:
5) Emily Lakdawalla, The Phoebe ring, The Planetary Society Blog, October 14, 2009, http://planetary.org/blog/article/00002165/
As Lakdawalla points out, discovering a big ring was just the beginning:
So far, it's a cool result but it's sort of like stamp collecting - we discovered a new X and described it, done. Where the paper gets really interesting is when the authors explore what happens to the particles in Phoebe's ring over time, something that you can model by writing down a few equations that describe the orbit of a particle, include Saturn, Phoebe, Iapetus, and Titan, include the masses, densities, and albedos of the particles, and the effects of incident sunlight.What happens to particles depends upon their size. The biggest chunks, several centimeters in size or larger, don't really migrate anywhere, sticking around near Phoebe's orbit until they smack into something - each other or Phoebe. The model simulation suggests that it would take more than the age of the solar system for half of the particles to be removed from the system by re-collision with Phoebe, so most of the biggest chunks are still out there somewhere in Phoebe's orbital space.
What about smaller particles? The article says "re-radiation of absorbed sunlight exerts an asymmetric force on dust grains, causing them to spiral in towards Saturn with a characteristic timescale of 1.5 × 105 r years, where r is the particle radius in micrometers. This force brings all centimetre-sized and smaller material to Iapetus and Titan unless mutual particle collisions occur first.... Most material from 10 micrometres to centimetres in size ultimately hits Iapetus, with smaller percentages striking Hyperion and Titan." This would be a slow process that has operated continuously since whenever Phoebe was captured into Saturn's orbit. There might have been bursts of material delivered to Iapetus associated with some of the bigger impacts that have left such large scars on Phoebe, but they would have been blips above a steady background.
Next: tilings. The science fiction writer Greg Egan is also a
professional programmer, and he's written a remarkable collection
of Java applets, which you can see on his website. Here's the latest:
6) Greg Egan, Girih, http://www.gregegan.net/APPLETS/32/32.html
This program generates quasiperiodic tilings with approximate 10-fold
rotational symmetry using a method called "inflation". The idea of
inflation is to take a collection of tiles and repeatedly subdivide
each one into smaller tiles from the same collection. Egan's applet
shows the process of inflation at work: patterns zooming in endlessly!
Some of the math behind this is modern, but some goes back to the Timurids:
the dynasty founded by the famous conqueror Timur, also known as
Tamerlane. By 1400, the Timurid empire was huge. It included most of
central Asia, Iran, and Afghanistan, as well as large parts of
Pakistan, India, Mesopotamia and the Caucasus. Its capital was the
magical city of Samarkand.
The Timurids raised the art of tiling to its highest peak. Islamic
artists had already explored periodic tilings with most of the 17
mathematically possible "wallpaper groups" as symmetries - for more on
this, see my tour of the Alhambra in "week267". What was left to do? Well,
periodic tilings can have 2-fold, 3-fold, 4-fold, or 6-fold rotational
symmetry, but nothing else. Notice the gap? It's the number 5! So
that's what they tackled.
Precisely because you can't produce periodic tilings with 5-fold
rotational symmetry, it's a delightful artistic challenge to fool
the careless eye into thinking you've done just that.
In the 1970's, Penrose discovered quasiperiodic patterns with
approximate 5-fold symmetry - for example, patterns made of two
tiles, called "kites" and "darts":
The work of Penrose launched a huge investigation into quasiperiodic
tilings and quasicrystals. With their eyes opened, modern scientists
saw how fascinating the old Timurid tilings were:
7) Peter J. Lu and Paul J. Steinhardt, Decagonal and quasi-crystalline
tilings in medieval Islamic architecture, Science 315 (2007), 1106-1110.
Lu and Steinhardt described a set of 5 tiles which seem to underlie a
lot of Timurid designs:
All the edges of all these tiles have the same length:
There are lots of ways to fit them together. The rhombus can be
subdivided into a kite and a dart, too!
Lu and Steinhardt call them "girih tiles". But
"girih" actually means "strapwork": the braided
bands that decorate the tiles in a lot of this art, as shown rather
crudely in the picture above. Egan's applet uses three of these
tiles: the decagon, the elongated hexagon and the bowtie. As you'll
see on his webpage, each can be subdivided into smaller decagons,
hexagons and bowties. And that's how "inflation" works.
Did the Timurid artists actually understand the process of inflation,
or the idea of a quasiperiodic tiling? Seeking clues, scholars have
turned to the Topkapi Scroll, a kind of "how-to manual" for tiling
that resides in the Topkapi Palace in Istanbul.
I would love to get my paws on this color reproduction:
8) Gulru Necipoglu and Mohammad al-Asad, The Topkapi Scroll - Geometry
and Ornament in Islamic Architecture, Getty Publications, 1996.
For now, the best substitute I've found is this beautiful article:
9) Peter R. Cromwell, The search for quasi-periodicity in Islamic
5-fold ornament, Math. Intelligencer 31 (2009), 36-56.
Also available at
http://www.springerlink.com/content/760261153n347478/?p=405b9dbf45ea4f4793a097b6e12dcb08pi=7
The Mathematical Intelligencer is a wonderful magazine put out by
Springer Verlag. It's recently become available online - and to my
shock, the above article is free! Springer doesn't give much away,
so I can't help but fear this is an oversight on their part, soon to
be corrected. So, grab a copy of this article now.
Cromwell argues that we shouldn't attribute too much modern
mathematical knowledge to the Timurid tile artists. But the really
great thing about this article is the detailed information on how some
of these tiling patterns are made - including lots of pictures. It
repays repeated study.
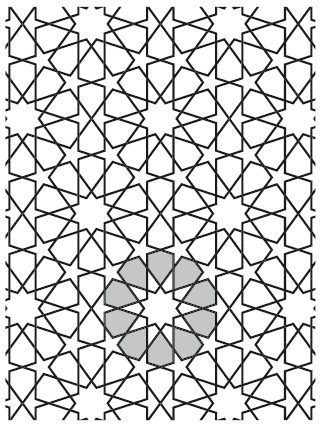
For an easy example, consider these regular decagons surrounded
by regular pentagons and funky hexagons of a different sort than
those in the girih tiles:
By replacing each decagon with a 10-pointed star, each pentagon
with a 5-pointed star, and extending the lines outward in a clever
way, he gets this magnificent design - one of the most widespread
star patterns in Islamic art:
Here's a less mathematical and more historical introduction to the
Timurid tile artists, also with lots of nice pictures:
10) Sebastian R. Prange, The tiles of infinity, Saudi Aramco World
(October-November 2009), 24-31. Also available at
http://www.saudiaramcoworld.com/issue/200905/the.tiles.of.infinity.htm
You should also check out Craig Kaplan's work. He's studied Kepler's
work on patterns built from decagons, and written software that
generates beautiful star patterns:
11) Craig Kaplan, The trouble with five, Plus Magazine 45 (December
2007), available at
http://plus.maths.org/issue45/features/kaplan/
12) Craig Kaplan, A meditation on Kepler's Aa, in Bridges 2006:
Mathematical Connections in Art, Music and Science, 2006, pp. 465-472.
Also available at http://www.cgl.uwaterloo.ca/~csk/papers/bridges2006a.html
13) Craig Kaplan, Taprats: computer generated Islamic star
patterns, http://www.cgl.uwaterloo.ca/~csk/washington/taprats/
Together with David Salesin, he's also gone beyond the old masters by
studying tilings in spherical and hyperbolic geometry:
14) Craig S. Kaplan and David H. Salesin, Islamic star patterns in
absolute geometry, ACM Transactions on Graphics 23 (April 2004),
97-119. Also available at
http://www.cgl.uwaterloo.ca/~csk/papers/tog2004.html
Another key player in this business is Eric Broug:
15) Broug Ateliers: Islamic Geometric Design, http://www.broug.com/
Check out the nice photo gallery and the lesson on 5-fold
symmetry! He sells beautiful screens and other products. But I
bought this book, which explains how
to make the patterns yourself:
16) Eric Broug, Islamic Geometric Patterns (book with CD-ROM), Thames
and Hudson, 2008.
Even if you don't have the skill or time to draw these patterns, the
book is worthwhile for the pictures and explanations.
I'll list a bunch more references below, for when I retire and get
time to devote myself more deeply to this subject. But now - on to
Corfu!
Last time I said a bit about what I learned in Ashtekar and Rovelli's
courses. Now I'd like to talk about some other things I learned in
Corfu - some things I find even more tantalizing.
In "week232", I explained how
gravity in 3d spacetime automatically contains within it a theory of
point particles, and how a 4d analogue of 3d gravity automatically
contains within it a theory of string-like objects. This 4d theory is
called BF theory. Like 3d gravity, it describes a world where
spacetime is flat. So, it's boring compared to full-fledged 4d
gravity - so boring that we can understand it much better! In
particular, unlike 4d gravity, we understand a lot about what happens
when you take quantum mechanics into account in 4d BF theory.
But when you remove a surface from spacetime in 4d BF
theory, it springs to life! In particular, the surface acts
a bit like the worldsheet of a string. It doesn't behave like the
strings in ordinary string theory. But Winston Fairbairn has
been thinking about this a lot:
17) Winston J. Fairbairn and Alejandro Perez, Extended matter coupled
to BF theory, Phys. Rev. D78:024013, 2008. Also available as
arXiv:0709.4235.
18) Winston J. Fairbairn, On gravitational defects, particles and
strings, JHEP 0809:126, 2008. Also available as arXiv:0807.3188.
19) Winston J. Fairbairn, Karim Noui and Francesco Sardelli, Canonical
analysis of algebraic string actions, available as arXiv:0908.0953
And it turns out that if we impose the constraints on BF theory that
turn it into general relativity, we obtain the usual Nambu-Goto
string, where the action is the area! However, the last of the three
papers above shows there are some subtle differences.
I need to think about this a lot more. It was always my hope to
reconcile string theory and loop quantum gravity, and this could be
the way. Of course, reconciling two things that don't work doesn't
necessarily give one that does. A pessimist might say that
combining string theory and loop quantum gravity is like combining epicycles
and aether. But I'm optimistic. Something interesting is going on here.
In a different but possibly related direction, Aristide Baratin gave
a talk on recent work he's been doing with Derek Wise and Laurent
Freidel. You can get a feel for this work from this paper:
20) Aristide Baratin, Derek K. Wise, 2-Group representations for spin
foams, to appear in proceedings of the XXV Max Born Symposium:
The Planck Scale, Wroclaw, Poland. Also available as
arXiv:0910.1542.
In "week235" I mentioned an
amazing paper by Baratin and Freidel called "Hidden quantum
gravity in 4d Feynman diagrams: emergence of spin foams". They
described a spin foam model that acts just like 4-dimensional flat
Minkowski spacetime: couple it to interacting point particles, and you
get the usual Feynman diagrams described in a new way!
The big news is that this spin foam model comes from the
representations of a 2-group, instead of a group. Namely, the
Poincaré 2-group. This is a 2-group I invented which has Lorentz
transformations as objects and translations as endomorphisms of any
object.
The Poincaré 2-group spin foam model was first studied by Crane,
Sheppeard and Yetter. Baratin, Freidel, Wise and I spent a long time
developing the theory of infinite-dimensional representations of
2-groups needed to make this model precise - see "week274" for more on all this. Now the details are
falling into place, and a beautiful picture is emerging.
I should admit that the paper by Baratin and Wise deals with the
Euclidean rather the Lorentzian version of this picture. I hope this
is merely because the representation theory of the "Euclidean
2-group" is more tractable than that of the Poincaré 2-group. I
hope everything generalizes to the Lorentzian case.
A lot to think about.
To wrap up, here's a big list of references from Cromwell's paper on
tilings I hadn't known so much had been written about this subject!
21) M. Arik and M. Sancak, Turkish-Islamic art and Penrose
tilings, Balkan Physics Letters 15 (1 Jul 2007) 1-12.
22) J. Bonner, Three traditions of self-similarity in fourteenth
and fifteenth century Islamic geometric ornament, Proc.
ISAMA/Bridges: Mathematical Connections in Art, Music and Science,
(Granada, 2003), eds. R. Sarhangi and N. Friedman, 2003, pp. 1-12.
23) J. Bonner, Islamic Geometric Patterns: Their Historical Development
and Traditional Methods of Derivation, unpublished manuscript.
24) J. Bourgoin, Les Elements de l'Art Arabe: Le Trait des Entrelacs,
Firmin-Didot, 1879. Plates reprinted in Arabic Geometric Pattern and
Design, Dover Publications, 1973.
25) J.-M. Castira, Arabesques: Art Decoratif au Maroc, ACR Edition,
1996.
26) J.-M. Castira, Zellijs, muqarnas and quasicrystals, Proc. ISAMA,
(San Sebastian, 1999), eds. N. Friedman and J. Barrallo, 1999, pp.
99-104.
27) G. M. Fleurent, Pentagon and decagon designs in Islamic art,
Fivefold Symmetry, ed. I. Hargittai, World Scientific, 1992, pp.
263-281.
28) B. Grunbaum and G. C. Shephard, Tilings and Patterns, W. H.
Freeman, 1987.
29) E. H. Hankin, On some discoveries of the methods of design employed
in Mohammedan art, J. Society of Arts 53 (1905) 461-477.
30) E. H. Hankin, The Drawing of Geometric Patterns in Saracenic Art,
Memoirs of the Archaeological Society of India, no 15, Government of
India, 1925.
31) E. H. Hankin, Examples of methods of drawing geometrical arabesque
patterns, Math. Gazette 12 (1925), 370-373.
32) E. H. Hankin, Some difficult Saracenic designs II, Math. Gazette
18 (1934), 165-168.
33) E. H. Hankin, Some difficult Saracenic designs III, Math. Gazette
20 (1936), 318-319.
34) A. J. Lee, Islamic star patterns, Muqarnas IV: An Annual on
Islamic Art and Architecture, ed. O. Grabar, Leiden, 1987, pp. 182.197.
35) P. J. Lu and P. J. Steinhardt, Response to Comment on "Decagonal
and quasi-crystalline tilings in medieval Islamic architecture",
Science 318 (30 Nov 2007), 1383.
36). F. Lunnon and P. Pleasants, Quasicrystallographic tilings, J.
Math. Pures et Appliques 66 (1987), 217-263.
37) E. Makovicky, 800-year old pentagonal tiling from Maragha, Iran,
and the new varieties of aperiodic tiling it inspired, Fivefold
Symmetry, ed. I. Hargittai, World Scientific, 1992, pp. 67-86.
38) E. Makovicky, Comment on "Decagonal and quasi-crystalline tilings
in medieval Islamic architecture", Science 318 (30 Nov 2007), 1383.
39) E. Makovicky and P. Fenoll Hach-Alm, Mirador de Lindaraja: Islamic
ornamental patterns based on quasi-periodic octagonal lattices
in Alhambra, Granada, and Alcazar, Sevilla, Spain, Boletin Sociedad
Espanola Mineralogia 19 (1996), 1-26.
40) E. Makovicky and P. Fenoll Hach-Alm, The stalactite dome of the
Sala de Dos Hermanas - an octagonal tiling?, Boletin Sociedad Espanola
Mineralogia 24 (2001), 1-21.
41) E. Makovicky, F. Rull Pirez and P. Fenoll Hach-Alm, Decagonal
patterns in the Islamic ornamental art of Spain and Morocco, Boletmn
Sociedad Espanola Mineralogia 21 (1998), 107-127.
42) J. Rigby, A Turkish interlacing pattern and the golden ratio,
Mathematics in School 34 no 1 (2005), 16-24.
43) J. Rigby, Creating Penrose-type Islamic interlacing patterns,
Proc. Bridges: Mathematical Connections in Art, Music and Science,
(London, 2006), eds. R. Sarhangi and J. Sharp, 2006, pp. 41-48.
44) F. Rull Pirez, La nocion de cuasi-cristal a traves de los mosaicos
arabes, Boletin Sociedad Espanola Mineralogia 10 (1987), 291-298.
45) P. W. Saltzman, Quasi-periodicity in Islamic ornamental design,
Nexus VII: Architecture and Mathematics, ed. K. Williams, 2008, pp.
153-168.
46) M. Senechal, Quasicrystals and Geometry, Cambridge Univ. Press,
1995.
47) M. Senechal and J. Taylor, Quasicrystals: The view from Les
Houches, Math. Intelligencer 12 (1990) 54-64.
Reference 24, the book by Bourgoin, is a classic - and the Dover version
is probably quite affordable. Cromwell also lists some more websites:
48) ArchNet, Library of digital images of Islamic architecture,
http://archnet.org/library/images/
49) E. Harriss and D. Frettlöh, Tilings Encyclopedia,
http://tilings.math.uni-bielefeld.de/
50) P. J. Lu and P. J. Steinhardt, Decagonal and quasi-crystalline
tilings in medieval Islamic architecture, supporting online material,
http://www.sciencemag.org/cgi/content/full/315/5815/1106/DC1
51) D. Wade, Pattern in Islamic Art: The Wade Photo-Archive,
http://www.patterninislamicart.com/
The last one is a huge treasure trove of images!
Addenda: Greg Egan writes:
This one can be run in full-screen mode.
I got an email
Craig Kaplan, whose
wonderful work on tilings I mentioned above. He writes:
52) Craig S. Kaplan, Islamic star patterns from polygons in contact,
in GI '05: Proceedings of the 2005 conference on Graphics Interface, 2005.
Also available at
http://www.cgl.uwaterloo.ca/~csk/papers/gi2005.html
Hope that's useful to you, and thanks for the mention.
53) Brian Wichmann, A tiling database,
http://www.tilingsearch.org/
Here's a database entry from the Alhambra:
Michael D. Hirschhorn emailed me to say that nearly 30 years ago, he
and David C. Hunt published a paper in the Journal of Combinatorial
Theory classifying all tilings of the plane by identical convex
equilateral pentagons. The most famous appears to be the "Hirschhorn
medallion" Bob Jenkins used
it to tile his bathroom:
Later Hirschhorn and Hunt extended their result to cover all
non-convex equilateral tilings, but this has never been
published.
Presumably this page is based on Hirschhorn and Hunt's work:
54) MathPuzzle, The 14 different types of convex pentagons that tile
the plane, available at http://www.mathpuzzle.com/tilepent.html
For more discussion visit the n-Category
Café.
The arabesques displayed a profound use of mathematical principles, and were made up
of obscurely symmetrical curves and angles based on the quantity of five. -
H. P. Lovecraft
© 2009 John Baez
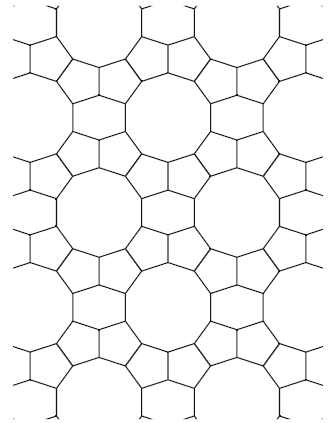
I wrote a new version of the Girih applet, which scrolls across an infinite
quasiperiodic tiling at a single scale. (I start with a Penrose rhombic
tiling that I construct by de Bruijn's method, and then convert into a
tiling of decagons, hexagons and bowties.)
Here's a sample of what it produces:
Because of the content of your post, I can't help but offer a few
notes about what you said. Feel free to use these any way you want,
or file them away for later.
Brian Wichmann pointed out this online database:
Hopefully they'll be out soon.

baez@math.removethis.ucr.andthis.edu

|
 
|

|