In the first talk of the ACT@UCR seminar, John Baez talked about work he did with Kenny Courser and Christina Vasilakopolou on network theory.
He gave his talk on Wednesday April 1st. Afterwards we discussed it on the Category Theory Community Server, here. You can view or join the conversation there if you sign in.
You can see his slides here, or download a video here, or watch the video here:
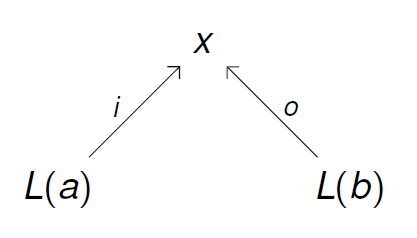
Abstract. One goal of applied category theory is to better understand networks appearing throughout science and engineering. Here we introduce "structured cospans" as a way to study networks with inputs and outputs. Given a functor L: A → X, a structured cospan is a diagram in X of the form

If A and X have finite colimits and L is a left adjoint, we obtain a symmetric monoidal category whose objects are those of A and whose morphisms are certain equivalence classes of structured cospans. However, this arises from a more fundamental structure: a symmetric monoidal double category where the horizontal 1-cells are structured cospans, not equivalence classes thereof. We explain the mathematics and illustrate it with an example from epidemiology.This talk was based on work with Kenny Courser and Christina Vasilakopoulou, some of which appears here:
He gave his talk on Wednesday April 8th. Afterwards we had discussions at the Category Theory Community Server, here. You can view or join the conversation there if you sign in.
You can see his slides here, or download a video here, or watch the video here:
Abstract. This talk is a fragment from a larger work on approximating Markov processes. I will focus on a functorial definition of conditional expectation without talking about how it was used. We define categories of cones—which are abstract versions of the familiar cones in vector spaces—of measures and related categories cones of Lp functions. We will state a number of dualities and isomorphisms between these categories. Then we will define conditional expectation by exploiting these dualities: it will turn out that we can define conditional expectation with respect to certain morphisms. These generalize the standard notion of conditioning with respect to a sub-sigma algebra. Why did I use the plural? Because it turns out that there are two kinds of conditional expectation, one of which looks like a left adjoint (in the matrix sense not the categorical sense) and the other looks like a right adjoint. I will review concepts like image measure, Radon-Nikodym derivatives and the traditional definition of conditional expectation. This is joint work with Philippe Chaput, Vincent Danos and Gordon Plotkin.For more, see:
He gave his talk on Wednesday April 15th. Afterwards we discussed it at the Category Theory Community Server, here. You can view or join the conversation there if you sign in.
You can see his slides here, or download a video here, or watch the video here:
Abstract. I will talk about open games, and the closely related concepts of lenses/optics and open learners. My goal is to report on the successes and failures of an ongoing effort to try to realise the often-claimed benefits of categories and compositionality in actual practice. I will introduce what little theory is needed along the way. Here are some things I plan to talk about:
- Lenses as an abstraction of the chain rule
- Comb diagrams
- Surprising applications of open games: Bayesian inference, value function iteration
- The state of tool support
- Open games in their natural habitat: microeconomics
- Sociological aspects of working with economics

He gave his talk on Wednesday April 22nd. He had to teach right after his talk, but he rejoined us for discussions later at the Category Theory Community Server, . You can view or join the conversation there if you sign in.
You can see his slides here, or download a video of his talk here, or watch the video here:
Abstract. Symmetric monoidal categories with duals, a.k.a. compact monoidal categories, have a pleasing string diagram calculus. In particular, any compact monoidal category is closed with [A,B] = (A* ⊗ B), and the transpose of A ⊗ B → C to A → [B,C] is represented by simply bending a string. Unfortunately, a closed symmetric monoidal category cannot even be embedded fully-faithfully into a compact one unless it is traced; and while string diagram calculi for closed monoidal categories have been proposed, they are more complicated, e.g. with "clasps" and "bubbles". In this talk we obtain a string diagram calculus for closed symmetric monoidal categories that looks almost like the compact case, by fully embedding any such category in a star-autonomous one (via a functor that preserves the closed structure) and using the known string diagram calculus for star-autonomous categories. No knowledge of star-autonomous categories will be assumed.His talk is based on this paper:

He gave his talk on Wednesday April 29th. Afterwards we discussed it at the Category Theory Community Server, here. You can view or join the conversation there if you sign in.
You can see his slides here, or download a video here, or watch the video here:
Abstract. Petri nets have been of interest to applied category theory for some time. Back in the 1980s, one approach to their semantics was given by algebraic gadgets called "event structures." We use classical techniques from order theory to study event structures without conflict restrictions (which we term "dependency structures with choice") by their associated "traces", which let us establish a one-to-one correspondence between DSCs and a certain class of locales. These locales have an internal logic of reachability, which can be equipped with "versioning" modalities that let us abstract away certain unnecessary detail from an underlying DSC. With this in hand we can give a general notion of what it means to "solve a dependency problem" and combinatorial results bounding the complexity of this. Time permitting, I will sketch work-in-progress which hopes to equip these locales with a notion of conflict, letting us capture the full semantics of general event structures in the form of homological data, thus providing one avenue to the topological semantics of concurrent systems. This is joint work with Raymond Puzio.

She gave her talk on May 6th, 2020. Afterwards we discussed it on the Category Theory Community Server, here. You can view or join the conversation there if you sign in.
You can see her slides here, or download a video of her talk here, or watch the video here:
Abstract. Separation logic aims to reason compositionally about the behavior of programs that manipulate shared resources. When working with separation logic, it is often necessary to manipulate information about program state in patterns of deconstruction and reconstruction. This achieves a kind of "focusing" effect which is somewhat reminiscent of using optics in a functional programming language. We make this analogy precise by showing that several interrelated techniques in the literature for managing these patterns of manipulation can be derived as instances of the general definition of profunctor optics. In doing so, we specialize the machinery of profunctor optics from categories to posets and to sets. This simplification makes most of this machinery look more familiar, and it reveals that much of it was already hiding in separation logic in plain sight.

She gave her talk on Wednesday May 13th. Afterwards we discussed her talk at the Category Theory Community Server, here. You can view or join the conversation there if you sign in.
You can see her slides here, or download a video here, or watch the video here:
Abstract. In this talk, I’ll show how any probability distribution on a product of finite sets gives rise to a pair of linear maps called density operators, whose eigenvectors capture “concepts” inherent in the original probability distribution. In some cases, the eigenvectors coincide with a simple construction from lattice theory known as a formal concept. In general, the operators recover marginal probabilities on their diagonals, and the information stored in their eigenvectors is akin to conditional probability. This is useful in an applied setting, where the eigenvectors and eigenvalues can be glued together to reconstruct joint probabilities. This naturally leads to a tensor network model of the original distribution. I’ll explain these ideas from the ground up, starting with an introduction to formal concepts. Time permitting, I’ll also share how the same ideas lead to a simple framework for modeling hierarchy in natural language. As an aside, it’s known that formal concepts arise as an enriched version of a generalization of the Isbell completion of a category. Oftentimes, the construction is motivated by drawing an analogy with elementary linear algebra. I like to think of this talk as an application of the linear algebraic side of that analogy.
Her talk is based on her thesis:

He gave his talk on Wednesday May 20th. Afterwards we discussed it on the Category Theory Community Server, here. You can view or join the conversation there if you sign in.
You can see his slides here, or download a video of his talk here, or watch his video here:
Abstract. We formalise the well-known rules of partial differentiation in a version of equational logic with function variables and binding constructs. We prove the resulting theory is complete with respect to polynomial interpretations. The proof makes use of Severi’s theorem that all multivariate Hermite problems are solvable. We also hope to present a number of related results, such as decidability and Hilbert--Post completeness.

He gave his talk on Wednesday May 27th. Afterwards we discussed it on the Category Theory Community Server, here. You can view or join the conversation there if you sign in.
You can see his slides here, or download a video here, or watch the video here:
Abstract. The Legendre-Fenchel transform is a classical piece of mathematics with many applications. In this talk I’ll show how it arises in the context of category theory using categories enriched over the extended real numbers [-∞,+∞]. It turns out that it arises out of nothing more than the pairing between a vector space and its dual in the same way that the many classical dualities (e.g. in Galois theory or algebraic geometry) arise from a relation between sets.The talk is based on this paper:I won’t assume knowledge of the Legendre-Fenchel transform.
The discussion took place on Wednesday June 3rd. Afterwards we had discussions at the Theory Community Server, here. You can view or join the conversation there if you sign in.
You can see her slides here, or download a video here, or watch the video here:
Abstract. Saddened by the current events, we are taking this opportunity to pause and reflect on what we can do to change the status quo and try to bring about real and long-lasting change. Thus, we are holding a discussion aimed at finding concrete solutions to make the Applied Category Theory community more inclusive, and also to reflect about the values that our community would like to stand for and endorse, in particular, in terms of which sources of funding go against our values. While this discussion is specific to the applied category theory community, we believe that many of the topics will be of interest also to people in other fields, and thus we welcome anybody with an interest to attend. The discussion will consist of two parts: we will have first several people give short talks to discuss common issues that we need to address, as well as present specific plans for initiatives that we could take. We believe that the current pandemic, and the fact that all activities are now taking place remotely, gives us the opportunity to involve people who would otherwise find it difficult to travel, because of disabilities, financial reasons or care-taking responsibilities. Thus, now we have the opportunity to come up with new types of mentoring, collaborations, and many other initiatives that might have been difficult to envision until just a couple of months ago. The second part of the discussion will take place on the category theory community server, and its purpose is to allow for a broader participation in the discussion, and ideally during this part we will be able to flesh out in detail the specific initiatives that have been proposed in the talks.