Mysteries of the gravitational 2-body problem

John Baez

January 18, 2022

The inverse square force law was the first really exciting test of classical mechanics: it describes the motion of a planet around the sun in the solar system. It's called the Kepler problem, since Kepler was the one who guessed that planets moved in ellipses, based on tables of empirical data. Later Hooke told Newton to see whether Newton's \(F = ma\) together with the inverse square force law would predict these elliptical orbits. Newton did just that, and went on to predict when Halley's comet would come back.

The inverse square force law was also the first really interesting test of quantum mechanics: it describes the motion of an electron around a proton in a hydrogen atom. A high school teacher named Balmer was the one who guessed the spectrum of hydrogen, based on tables of empirical data. Bohr came up with a rough-and-ready approach to quantum mechanics that explained Balmer's formula, but Schrödinger was the first to give a really detailed explanation.

In both cases the solution is "better than it needs to be". What I mean is this. In classical mechanics we can solve for the motion of a particle in any central force by doing an integral; if the force is attractive we'll get orbits that go round and round... but usually the orbits will precess. The magical thing about the inverse square force law

$$ F = -k/r^2 $$

is that they don't precess: we get closed orbits! This is also true for the harmonic oscillator, where the force is described by Hooke's other law:

$$ F = -kr $$

Even better, in both cases the motion is in an ellipse! It was an eerie stroke of luck for Newton that the Greeks — especially Apollonius — "just so happened" to have spent a lot of time studying conic sections just for their intrinsic beauty. That let Newton invent a proof using Euclidean geometry that the planets go around in ellipses, given classical mechanics and an inverse square force law. He probably figured this out using calculus, but in the Principia he hid his tracks, since calculus wasn't rigorous, while Euclid's Elements was regarded as the pinnacle of rigor.

In quantum mechanics we find that a hydrogen atom has \((n+1)^2\) bound states in the \(n\)th energy level, if we start counting at \(n = 0\). Again this is "better than it needs to be". For a typical central force we expect bound states of different total angular momentum to have different energies; but for the inverse square force law something magical happens: there are states of different total angular momenta having the same energy! The \(n\)th energy level has:

and so on, up to for a total of

$$1 + 3 + 5 + \cdots + 2n+1 = (n+1)^2$$

states. Here I'm not talking about subtleties involving spin, which double the count of states and split some of these energy levels. I'm just talking about Schrödinger's original calculation.

The reason for both these "magical effects" is the Runge–Lenz vector: an extra conserved quantity besides energy and angular momentum, which is special to the inverse square force law! The formula for it looks pretty weird: $$ \frac{v \times J}{k} - \frac{q}{|q|} $$ where:

To understand the meaning of the Runge–Lenz vector, you need to know two things about it:

So, the fact that it's conserved means the orbit doesn't precess, and doesn't get more skinny or round as time passes.

For a proof of these facts, a proof that the Runge–Lenz vector is conserved, and an argument that uses it to deduce that the orbits in an inverse square force law are conic sections, try these homework problems of mine:

Both classically and quantum mechanically, Noether's theorem relates conserved quantities and symmetries, so the fact that the Runge–Lenz vector is conserved means the inverse square force law has more symmetry than your average central force. But it's a rather sneaky "hidden symmetry", which changes the eccentricity of the orbits! For a great explanation of this, go here:

I'll just quote a tiny bit:
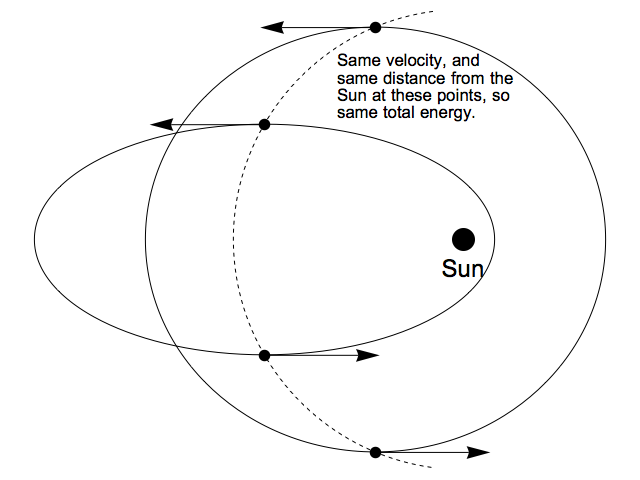
Now, one way to find orbits with the same energy is by applying a rotation that leaves the sun fixed but repositions the planet. Any ordinary three-dimensional rotation can be used in this way, yielding another orbit with exactly the same shape, but oriented differently.

But there is another transformation we can use to give us a new orbit without changing the total energy. If we grab hold of the planet at either of the points where it's travelling parallel to the axis of the ellipse, and then swing it along a circular arc centred on the sun, we can reposition it without altering its distance from the sun. But rather than rotating its velocity in the same fashion (as we would do if we wanted to rotate the orbit as a whole) we leave its velocity vector unchanged: its direction, as well as its length, stays the same.

It's easy to see how this process changes the orbit's eccentricity.

The angular momentum and Runge–Lenz vector (rescaled by a function of the energy) give a total of 6 conserved quantities, which in turn generate a 6-dimensional group of symmetries. The nature of this group depends on whether we are looking at solutions with:

  1. negative energy: 'bound states', where the particle moves in an ellipse,
  2. positive energy: 'scattering states', where it moves in a hyperbola, or
  3. zero energy: states where the particle moves in a parabola.
Here's the symmetry group you get in each case:
  1. For negative-energy states, the 6-dimensional symmetry group you get is SO(4), the group of rotations in 4d space!

  2. For positive-energy states, the 6-dimensional symmmetry group you get is SO0(3,1), the connected component of the Lorentz group! This group is famous in special relativity... who'd have thought it was lurking in Newtonian gravity?

  3. For zero-energy states, the 6-dimensional symmetry group is ISO0(3), the connected component of the 3d Euclidean group! By this I mean the symmetry group of 3-dimensional Euclidean space, including rotations and translations.

Let's focus on the negative-energy states: the bound states. For each \(n\), SO(4) has an irreducible representation of dimension \((n+1)^2\) which explains why the hydrogen atom has this many bound states in the \(n\)th energy level, discounting spin.

Now, you've probably seen those cute pictures where people draw an atom like a tiny little solar system, with electrons racing around in elliptical orbits. This is silly because it neglects the big difference between classical and quantum mechanics. The uncertainty principle means that electrons don't have well-defined orbits!

But, the analogy between the atom and the solar system becomes rather deep if relate the two using geometric quantization. If you've got just one planet orbiting the sun in an ellipse, or just one electron orbiting your nucleus, you've got a system where the Runge–Lenz vector, you've got a system with SO(4) symmetry! — and quantizing the first gives the second.

If you want more details, read this:

This is required reading for anyone interested in the hidden symmetries of the Kepler problem.

But what's the "real reason" why the Kepler problem has extra hidden symmetries?

Guillemin and Sternberg's book shows that if we only consider the bound states of the Kepler problem, we get a physics problem that closely allied to the motion of a free point particle on the unit sphere in 4d space! They're related by a "generalized canonical transformation", where we reparametrize time as well as changing the other variables. This is very beautiful, because mathematically this means we're looking at geodesic motion on S3, which is the same as SU(2), the double cover of the rotation group. However, Guillemin and Sternberg need a few yucky calculations to reach this conclusion, so the intuitions behind it are not completely clear.

Greg Egan's webpage brings out some of the key ideas more clearly. He explains the symmetries corresponding to the Runge–Lenz conserved quantities using this remarkable fact: as the particle moves around its elliptical orbit, its velocity vector moves in a circle!

According to John Milnor, this fact was noted by Hamilton in 1846:

Then, following the work of Fock and others, Egan exploits this fact to show how the Kepler problem is related to a free particle on S3 — both classically and quantum-mechanically!

Why ellipses?

It's also somewhat mysterious that an object moving in an inverse square force law traces out a conic section. There are lots of ways to prove it, of course. Newton did it using Euclidean geometry. My homework problems above give two other ways. The one using the Runge–Lenz vector is pretty... but I'm still looking for the most beautiful way, where you leave the room saying: "Inverse square force law... conic sections... of course! Now the connection is obvious!"

You can see some nice proofs in this webpage by Greg Egan:

One of my favorites is the 'squared harmonic oscillator proof', which I first saw here:

It goes like this. Look at a harmonic oscillator in 2 dimensions. The particle's orbit is an ellipse in the plane with its center at the origin. Think of this plane as the complex plane and apply the transformation $$ z \mapsto z^2 = Z $$ This sends that ellipse to an ellipse with one focus at the origin! Then, replace time by a new parameter \(s\) with $$ \frac{d s}{dt} = |Z| $$ As a function of this new time parameter \(s\), the point \(Z\) moves in a way that solves the Kepler problem!

That's pretty amazing. I thought the two most important problems in classical mechanics were the harmonic oscillator and the Kepler problem. It turns out they're secretly the same problem in disguise.

For more details on this clever trick, see:

For even more, see the discussion of Göransson's work below. Göransson uses the same reparametrization of time, but does something startlingly different with it.

For yet another perspective on how the inverse square law leads to elliptical orbits, try the argument in Feynman's "lost lecture":

He gives a fascinating argument, but it's not what I'd call truly beautiful. Still, the book is definitely worth reading. I didn't listen to the CD that came with it, but I'm sure that's fun too.

Göransson's work

After this page had been on my website for years, I got an mail from a self-described "amateur" that clarified many of the mysteries described above: It simultaneously explains why planets move in elliptical orbits and why you can apply a 4-dimensional rotation to an elliptical orbit and get another elliptical orbit with the same energy.

In fact, they planets are moving in circles in 4 dimensions. But when these circles are projected down to 3-dimensional space, they become ellipses!

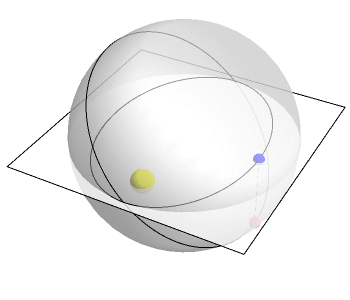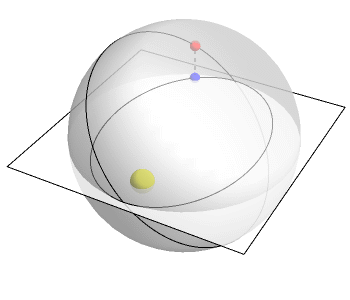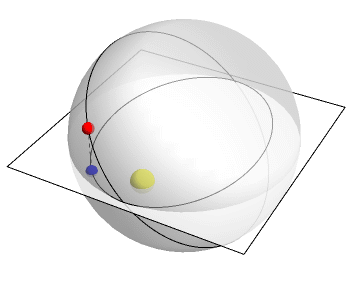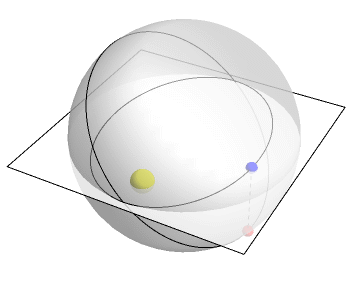
This animation by Greg Egan shows the idea:

The plane here represents 2 of the 3 space dimensions we live in. The vertical direction is the mysterious fourth dimension. The planet goes around in a circle in 4-dimensional space. But down here in 3 dimensions, its 'shadow' moves in an ellipse!

What's this fourth dimension I'm talking about here? It's a lot like time. But it's not exactly time. It's the difference between ordinary time and another sort of time, which flows at a rate inversely proportional to the distance between the planet and the sun.

The movie uses this other sort of time. Relative to this other time, the planet is moving at constant speed around a circle in 4 dimensions. But in ordinary time, its shadow in 3 dimensions moves faster when it's closer to the sun.

All this sounds crazy, but it's not some new physics theory. It's just a different way of thinking about Newtonian physics!

The best thing about this way of thinking is that it gives a clean explanation of an amazing fact I mentioned earlier: you can take any elliptical orbit, apply a rotation of 4-dimensional space, and get another valid orbit!

Of course we can rotate an elliptical orbit about the sun in the usual 3-dimensional way and get another elliptical orbit. The interesting part is that we can also do 4-dimensional rotations. This can make a round ellipse look skinny: when we tilt a circle into the fourth dimension, its 'shadow' in 3-dimensional space becomes thinner!

In fact, you can turn any elliptical orbit into any other elliptical orbit with the same energy by a 4-dimensional rotation of this sort. All elliptical orbits with the same energy are really just circular orbits on the same sphere in 4 dimensions!

Jesper Göransson's paper explains how this works in a terse and elegant way. But I can't resist summarizing the key results.

Göransson's results

Suppose we have a particle moving in an inverse square force law. Its equation of motion is $$ \displaystyle{ m \ddot{\mathbf{r}} = - \frac{k \mathbf{r}}{r^3} } $$ where \(\mathbf{r}\) is its position as a function of time, \(r\) is its distance from the origin, \(m\) is its mass, and \(k\) says how strong the force is. From this we can derive the law of conservation of energy, which says $$ \displaystyle{ \frac{m \dot{\mathbf{r}} \cdot \dot{\mathbf{r}}}{2} - \frac{k}{r} = E } $$ for some constant \(E\) that depends on the particle's orbit, but doesn't change with time.

Let's consider an attractive force, so \(k > 0\), and elliptical orbits, so \(E < 0\), Let's call the particle a 'planet'. It's a planet moving around the sun, where we treat the sun as so heavy that it remains perfectly fixed at the origin.

I only want to study orbits of a single fixed energy \(E\). This frees us to choose units of mass, length and time in which $$ m = 1, \;\; k = 1, \;\; E = -\frac{1}{2} $$ This will reduce the clutter of letters and let us focus on the key ideas. If you prefer an approach that keeps in the units, see Göransson's paper.

Now the equation of motion is $$ \displaystyle{\ddot{\mathbf{r}} = - \frac{\mathbf{r}}{r^3} } $$ and conservation of energy says $$ \displaystyle{ \frac{\dot{\mathbf{r}} \cdot \dot{\mathbf{r}}}{2} - \frac{1}{r} = -\frac{1}{2} } $$ The big idea — discovered earlier by someone else — is to switch from our ordinary notion of time to a new notion of time! We'll call this new time \(s\), and demand that $$ \displaystyle{ \frac{d s}{d t} = \frac{1}{r} } $$ This new kind of time ticks more slowly as you get farther from the sun. So, using this new time speeds up the planet's motion when it's far from the sun. If that seems backwards, just think about it. For a planet very far from the sun, one day of this new time could equal a week of ordinary time. So, measured using this new time, a planet far from the sun might travel in one day what would normally take a week.

This compensates for the planet's ordinary tendency to move slower when it's far from the sun. In fact, with this new kind of time, a planet moves just as fast when it's farthest from the sun as when it's closest.

Amazing stuff happens with this new notion of time!

To see this, first rewrite conservation of energy using this new notion of time. I've been using a dot for the ordinary time derivative, following Newton. Let's use a prime for the derivative with respect to \(s\). So, for example, we have $$ \displaystyle{ t' = \frac{dt}{ds} = r } $$ and $$ \displaystyle{ \mathbf{r}' = \frac{dr}{ds} = \frac{dt}{ds}\frac{dr}{dt} = r \dot{\mathbf{r}} } $$ Using this new kind of time derivative, Göransson shows that conservation of energy can be written as $$ \displaystyle{ (t' - 1)^2 + \mathbf{r}' \cdot \mathbf{r}' = 1 } $$ This is the equation of a sphere in 4-dimensional space!

I'll prove this later. First let's talk about what it means. To understand it, we should treat the ordinary time coordinate \(t\) and the space coordinates \((x,y,z)\) on an equal footing. The point $$ (t,x,y,z) $$ moves around in 4-dimensional space as the parameter \(s\) changes. What we're seeing is that the velocity of this point, namely $$ \mathbf{v} = (t',x',y',z') $$ moves around on a sphere in 4-dimensional space! It's a sphere of radius one centered at the point $$ (1,0,0,0) $$ With some further calculation we can show some other wonderful facts: $$ \mathbf{r}''' = -\mathbf{r}' $$ and $$ t''' = -(t' - 1) $$ These are the usual equations for a harmonic oscillator, but with an extra derivative!

I'll prove these wonderful facts later. For now let's just think about what they mean. We can state both of them in words as follows: the 4-dimensional velocity \(\mathbf{v}\) carries out simple harmonic motion about the point \((1,0,0,0)\).

That's nice. But since \(\mathbf{v}\) also stays on the unit sphere centered at this point, we can conclude something even better: \(v\) must move along a great circle on this sphere, at constant speed!

This implies that the spatial components of the 4-dimensional velocity have mean \(0\), while the \(t\) component has mean \(1\).

The first part here makes a lot of sense: our planet doesn't drift ever farther from the Sun, so its mean velocity must be zero. The second part is a bit subtler, but it also makes sense: the ordinary time \(t\) moves forward at speed 1 on average with respect to the new time parameter \(s\), but its rate of change oscillates in a sinusoidal way.

If we integrate both sides of $$ \mathbf{r}''' = -\mathbf{r}' $$ we get $$ \mathbf{r}'' = -\mathbf{r} + \mathbf{a} $$ for some constant vector \(\mathbf{a}\). This says that the position \(\mathbf{r}\) oscillates harmonically about a point \(\mathbf{a}\). Since \( \mathbf{a}\) doesn't change with time, it's a conserved quantity: it's essentially the Runge–Lenz vector.

Often people start with the inverse square force law, show that angular momentum and the Runge–Lenz vector are conserved, and use these 6 conserved quantities and Noether's theorem to show there's a 6-dimensional group of symmetries. For solutions with negative energy, this turns out to be the group of rotations in 4 dimensions, \(\mathrm{SO}(4)\). With more work, we can see how the Kepler problem is related to a harmonic oscillator in 4 dimensions. Doing this involves reparametrizing time.

I like Göransson's approach better in many ways, because it starts by biting the bullet and reparametrizing time. This lets him rather efficiently show that the planet's elliptical orbit is a projection to 3-dimensional space of a circular orbit in 4d space. The 4d rotational symmetry is then evident!

Göransson actually carries out his argument for an inverse square law in n-dimensional space; it's no harder. The elliptical orbits in \(n\) dimensions are projections of circular orbits in \(n+1\) dimensions. Angular momentum is a bivector in n dimensions; together with the Runge–Lenz vector it forms a bivector in \(n+1\) dimensions. This is the conserved quantity associated to the \((n+1)\)-dimensional rotational symmetry of the problem.

He also carries out the analogous argument for positive-energy orbits, which are hyperbolas, and zero-energy orbits, which are parabolas. The hyperbolic case has the Lorentz group symmetry and the zero-energy case has Euclidean group symmetry! This was already known, of course, but it's nice to see how easily Göransson's calculations handle all three cases.

Mathematical details of Göransson's work

Checking all this is a straightforward exercise in vector calculus, but it takes a bit of work, so let me do some here. There will still be details left to fill in, and I urge that you give it a try, because this is the sort of thing that's more interesting to do than to watch.

There are a lot of equations coming up, so I'll put boxes around the important ones. The basic ones are the force law, conservation of energy, and the change of variables that gives $$ \boxed{ t' = r , \qquad \mathbf{r}' = r \dot{\mathbf{r}} } $$ We start with conservation of energy: $$ \boxed{ \displaystyle{ \frac{\dot{\mathbf{r}} \cdot \dot{\mathbf{r}}}{2} - \frac{1}{r} = -\frac{1}{2} } } $$ and then use $$ \displaystyle{ \dot{\mathbf{r}} = \frac{d\mathbf{r}/dt}{dt/ds} = \frac{\mathbf{r}'}{t'} } $$ to obtain $$ \displaystyle{ \frac{\mathbf{r}' \cdot \mathbf{r}'}{2 t'^2} - \frac{1}{t'} = -\frac{1}{2} } $$ With a little algebra this gives $$ \boxed{ \displaystyle{ \mathbf{r}' \cdot \mathbf{r}' + (t' - 1)^2 = 1} } $$ This shows that the '4-velocity' $$ \mathbf{v} = (t',x',y',z') $$ stays on the unit sphere centered at \((1,0,0,0)\). The next step is to take the equation of motion $$ \boxed{ \displaystyle{\ddot{\mathbf{r}} = - \frac{\mathbf{r}}{r^3} } } $$ and rewrite it using primes (\(s\) derivatives) instead of dots (\(t\) derivatives). We start with $$ \displaystyle{ \dot{\mathbf{r}} = \frac{\mathbf{r}'}{r} } $$ and differentiate again to get $$ \ddot{\mathbf{r}} = \displaystyle{ \frac{1}{r} \left(\frac{\mathbf{r}'}{r}\right)' } = \displaystyle{ \frac{1}{r} \left( \frac{r \mathbf{r}'' - r' \mathbf{r}'}{r^2} \right) } = \displaystyle{ \frac{r \mathbf{r}'' - r' \mathbf{r}'}{r^3} } $$ Now we use our other equation for \(\ddot{\mathbf{r}}\) and get $$ \displaystyle{ \frac{r \mathbf{r}'' - r' \mathbf{r}'}{r^3} = -\frac{\mathbf{r}}{r^3} } $$ or $$ r \mathbf{r}'' - r' \mathbf{r}' = -\mathbf{r} $$ so $$ \boxed{ \displaystyle{ \mathbf{r}'' = \frac{r' \mathbf{r}' - \mathbf{r}}{r} } } $$ To go further, it's good to get a formula for \(r''\) as well. First we compute $$ r' = \displaystyle{ \frac{d}{ds} (\mathbf{r} \cdot \mathbf{r})^{\frac{1}{2}} } = \displaystyle{ \frac{\mathbf{r}' \cdot \mathbf{r}}{r} } $$ and then differentiating again, $$ r'' = \displaystyle{\frac{d}{ds} \frac{\mathbf{r}' \cdot \mathbf{r}}{r} } = \displaystyle{ \frac{r \mathbf{r}'' \cdot \mathbf{r} + r \mathbf{r}' \cdot \mathbf{r}' - r' \mathbf{r}' \cdot \mathbf{r}}{r^2} } $$ Plugging in our formula for \(\mathbf{r}''\), some wonderful cancellations occur and we get $$ r'' = \displaystyle{ \frac{\mathbf{r}' \cdot \mathbf{r}'}{r} - 1 } $$ But we can do better! Remember, conservation of energy says $$ \displaystyle{ \mathbf{r}' \cdot \mathbf{r}' + (t' - 1)^2 = 1} $$ and we know \(t' = r\). So, $$ \mathbf{r}' \cdot \mathbf{r}' = 1 - (r - 1)^2 = 2r - r^2 $$ and $$ r'' = \displaystyle{ \frac{\mathbf{r}' \cdot \mathbf{r}'}{r} - 1 } = 1 - r $$ So, we see $$ \boxed{ r'' = 1 - r } $$ Can you get here more elegantly? Since \(t' = r\) this instantly gives $$ \boxed{ t''' = 1 - t' } $$ as desired.

Now let's get a similar formula for \(\mathbf{r}'''\). We start with $$ \displaystyle{ \mathbf{r}'' = \frac{r' \mathbf{r}' - \mathbf{r}}{r} } $$ and differentiate both sides to get $$ \displaystyle{ \mathbf{r}''' = \frac{r r'' \mathbf{r}' + r r' \mathbf{r}'' - r \mathbf{r}' - r'}{r^2} } $$ Then plug in our formulas for \(r''\) and \(\mathbf{r}''\). Some truly miraculous cancellations occur and we get $$ \boxed{ \mathbf{r}''' = -\mathbf{r}' } $$ I could show you how it works—but to really believe it you have to do it yourself. It's just algebra. Again, I'd like a better way to see why this happens!

Integrating both sides—which is a bit weird, since we got this equation by differentiating both sides of another one—we get $$ \boxed{ \mathbf{r}'' = -\mathbf{r} + \mathbf{a} } $$ for some fixed vector \(\mathbf{a}\), which is essentially the Runge–Lenz vector. This says \(\mathbf{r}\) undergoes harmonic motion about \(\mathbf{a}\). It's quite remarkable that both \(\mathbf{r}\) and its norm \(r\) undergo harmonic motion! At first I thought this was impossible, but it's just a very special circumstance.

The Kepler problem and Jordan algebras

In 2011, Guowu Meng pointed out a remarkable fact to me. Orbits of the Kepler problem are precisely the intersections of 2-dimensional planes with this cone

$$ \{(t,x,y,z) : t^2 - x^2 - y^2 - z^2 = 0 , \; t \gt 0 \}$$ in 4-dimensional Minkowski spacetime! This should give another way of understanding the hidden SO0(3,1) symmetry of the scattering states of the Kepler problem.

Moreover, there is a generalized version of the Kepler problem for every formally real Jordan algebra, and the Kepler problem we know and love is related to the Jordan algebra of \(2 \times 2\) hermitian complex matrices, which can also be thought of as 4-dimensional Minkowski spacetime! For more, try:

The Kepler problem and supersymmetry

There's also a relation between the Kepler problem and supersymmetry. In the fall of 2011, Blake Stacey told me:
"The SUSY QM approach is how we solved the hydrogen atom in our undergrad quantum class at MIT."
For more, see: The last paper relates supersymmetry to the Runge–Lenz vector!

To dig deeper

Here are some more references:

Finally, just for fun, we can use the SO(4) symmetry of the hydrogen atom to construct wavefunctions invariant under discrete subgroups of SO(4). Here is one, drawn by Greg Egan, which is an energy eigenstate that's also invariant under the rotational symmetry group of the 600-cell, a 4-dimensional regular polytope.

For more, read this:

Is not this, perhaps, the secret of every true and great mystery, that it is simple? - C. Kerenyi

© 2018 John Baez
baez@math.removethis.ucr.andthis.edu

home