SMB2021
June 14-17, 2021

Non-Equilibrium Thermodynamics in Biology:
from Chemical Reaction Networks to Natural Selection

Since Lotka, physical scientists have argued that living things belong to a class of complex and orderly systems that exist not despite the second law of thermodynamics, but because of it. Life and evolution, through natural selection of dissipative structures, are based on non-equilibrium thermodynamics. The challenge is to develop an understanding of what the respective physical laws can tell us about flows of energy and matter in living systems, and about growth, death and selection. This session will address current challenges including understanding emergence, regulation and control across scales, and entropy production, from metabolism in microbes to evolving ecosystems.

• Persistence, permanence, and global stability in reaction network models: some results inspired by thermodynamic principles
  Gheorghe Craciun, University of Wisconsin–Madison

  The standard mathematical model for the dynamics of concentrations in biochemical networks is called mass-action kinetics. We describe mass-action kinetics and discuss the connection between special classes of mass-action systems (such as detailed balanced and complex balanced systems) and the Boltzmann equation. We also discuss the connection between the 'global attractor conjecture' for complex balanced mass-action systems and Boltzmann's H-theorem. We also describe some implications for biochemical mechanisms that implement noise filtering and cellular homeostasis.

• The principle of maximum caliber of nonequilibria
  Ken Dill, Stony Brook University

  Maximum Caliber is a principle for inferring pathways and rate distributions of kinetic processes. The structure and foundations of MaxCal are much like those of Maximum Entropy for static distributions. We have explored how MaxCal may serve as a general variational principle for nonequilibrium statistical physics - giving well-known results, such as the Green-Kubo relations, Onsager's reciprocal relations and Prigogine's Minimum Entropy Production principle near equilibrium, but is also applicable far from equilibrium. I will also discuss some applications, such as finding reaction coordinates in molecular simulations non-linear dynamics in gene circuits, power-law-tail distributions in 'social-physics' networks, and others.

• Nonequilibrium biomolecular information processes
  Pierre Gaspard, Université libre de Bruxelles

  Nearly 70 years have passed since the discovery of DNA structure and its role in coding genetic information. Yet, the kinetics and thermodynamics of genetic information processing in DNA replication, transcription, and translation remain poorly understood. These template-directed copolymerization processes are running away from equilibrium, being powered by extracellular energy sources. Recent advances show that their kinetic equations can be exactly solved in terms of so-called iterated function systems. Remarkably, iterated function systems can determine the effects of genome sequence on replication errors, up to a million times faster than kinetic Monte Carlo algorithms. With these new methods, fundamental links can be established between molecular information processing and the second law of thermodynamics, shedding a new light on genetic drift, mutations, and evolution.

• Nonequilibrium dynamics of disturbed ecosystems
  John Harte, University of California, Berkeley

  The Maximum Entropy Theory of Ecology (METE) predicts the shapes of macroecological metrics in relatively static ecosystems, across spatial scales, taxonomic categories, and habitats, using constraints imposed by static state variables. In disturbed ecosystems, however, with time-varying state variables, its predictions often fail. We extend macroecological theory from static to dynamic, by combining the MaxEnt inference procedure with explicit mechanisms governing disturbance. In the static limit, the resulting theory, DynaMETE, reduces to METE but also predicts a new scaling relationship among static state variables. Under disturbances, expressed as shifts in demographic, ontogenic growth, or migration rates, DynaMETE predicts the time trajectories of the state variables as well as the time-varying shapes of macroecological metrics such as the species abundance distribution and the distribution of metabolic rates over individuals. An iterative procedure for solving the dynamic theory is presented. Characteristic signatures of the deviation from static predictions of macroecological patterns are shown to result from different kinds of disturbance. By combining MaxEnt inference with explicit dynamical mechanisms of disturbance, DynaMETE is a candidate theory of macroecology for ecosystems responding to anthropogenic or natural disturbances.

• Stochastic chemical reaction networks
  Supriya Krishnamurthy, Stockholm University

  The study of chemical reaction networks (CRN's) is a very active field. Earlier well-known results (Feinberg Chem. Enc. Sci. 42 2229 (1987), Anderson et al Bull. Math. Biol. 72 1947 (2010)) identify a topological quantity called deficiency, easy to compute for CRNs of any size, which, when exactly equal to zero, leads to a unique factorized (non-equilibrium) steady-state for these networks. No general results exist however for the steady states of non-zero-deficiency networks. In recent work, we show how to write the full moment-hierarchy for any non-zero-deficiency CRN obeying mass-action kinetics, in terms of equations for the factorial moments. Using these, we can recursively predict values for lower moments from higher moments, reversing the procedure usually used to solve moment hierarchies. We show, for non-trivial examples, that in this manner we can predict any moment of interest, for CRN's with non-zero deficiency and non-factorizable steady states. It is however an open question how scalable these techniques are for large networks.

• Heat flows adjust local ion concentrations in favor of prebiotic chemistry
  Christof Mast, Ludwig-Maximilians-Universität München

  Prebiotic reactions often require certain initial concentrations of ions. For example, the activity of RNA enzymes requires a lot of divalent magnesium salt, whereas too much monovalent sodium salt leads to a reduction in enzyme function. However, it is known from leaching experiments that prebiotically relevant geomaterial such as basalt releases mainly a lot of sodium and only little magnesium. A natural solution to this problem is heat fluxes through thin rock fractures, through which magnesium is actively enriched and sodium is depleted by thermogravitational convection and thermophoresis. This process establishes suitable conditions for ribozyme function from a basaltic leach. It can take place in a spatially distributed system of rock cracks and is therefore particularly stable to natural fluctuations and disturbances.

• Deficiency of chemical reaction networks and thermodynamics
  Matteo Polettini, University of Luxembourg

  Deficiency is a topological property of a Chemical Reaction Network linked to important dynamical features, in particular of deterministic fixed points and of stochastic stationary states. Here we link it to thermodynamics: in particular we discuss the validity of a strong vs. weak zeroth law, the existence of time-reversed mass-action kinetics, and the possibility to formulate marginal fluctuation relations. Finally we illustrate some subtleties of the Python module we created for MCMC stochastic simulation of CRNs, soon to be made public.

• Large deviations theory and emergent landscapes in biological dynamics
  Hong Qian, University of Washington

  The mathematical theory of large deviations provides a nonequilibrium thermodynamic description of complex biological systems that consist of heterogeneous individuals. In terms of the notions of stochastic elementary reactions and pure kinetic species, the continuous-time, integer-valued Markov process dictates a thermodynamic structure that generalizes (i) Gibbs’ macroscopic chemical thermodynamics of equilibrium matters to nonequilibrium small systems such as living cells and tissues; and (ii) Gibbs’ potential function to the landscapes for biological dynamics, such as that of C. H. Waddington’s and S. Wright’s.

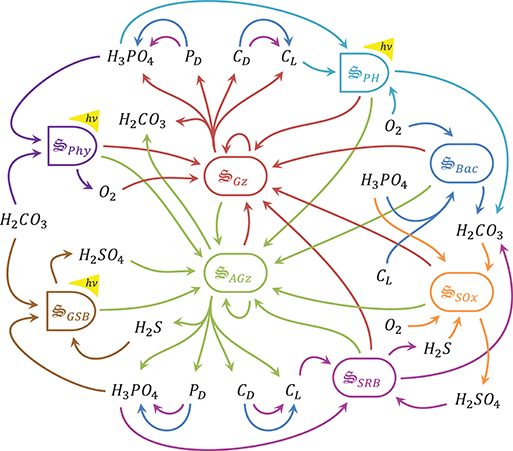
• Using the maximum entropy production principle to understand and predict microbial biogeochemistry
  Joseph Vallino, Marine Biological Laboratory, Woods Hole

  Natural microbial communities contain billions of individuals per liter and can exceed a trillion cells per liter in sediments, as well as harbor thousands of species in the same volume. The high species diversity contributes to extensive metabolic functional capabilities to extract chemical energy from the environment, such as methanogenesis, sulfate reduction, anaerobic photosynthesis, chemoautotrophy, and many others, most of which are only expressed by bacteria and archaea. Reductionist modeling of natural communities is problematic, as we lack knowledge on growth kinetics for most organisms and have even less understanding on the mechanisms governing predation, viral lysis, and predator avoidance in these systems. As a result, existing models that describe microbial communities contain dozens to hundreds of parameters, and state variables are extensively aggregated. Overall, the models are little more than non-linear parameter fitting exercises that have limited, to no, extrapolation potential, as there are few principles governing organization and function of complex self-assembling systems. Over the last decade, we have been developing a systems approach that models microbial communities as a distributed metabolic network that focuses on metabolic function rather than describing individuals or species. We use an optimization approach to determine which metabolic functions in the network should be up regulated versus those that should be down regulated based on the non-equilibrium thermodynamics principle of maximum entropy production (MEP). Derived from statistical mechanics, MEP proposes that steady state systems will likely organize to maximize free energy dissipation rate. We have extended this conjecture to apply to non-steady state systems and have proposed that living systems maximize entropy production integrated over time and space, while non-living systems maximize instantaneous entropy production. Our presentation will provide a brief overview of the theory and approach, as well as present several examples of applying MEP to describe the biogeochemistry of microbial systems in laboratory experiments and natural ecosystems.

• Reduction and the quasi-steady state approximation
  Carsten Wiuf, University of Copenhagen

  Chemical reactions often occur at different time-scales. In applications of chemical reaction network theory it is often desirable to reduce a reaction network to a smaller reaction network by elimination of fast species or fast reactions. There exist various techniques for doing so, e.g. the Quasi-Steady-State Approximation or the Rapid Equilibrium Approximation. However, these methods are not always mathematically justifiable. Here, a method is presented for which (so-called) non-interacting species are eliminated by means of QSSA. It is argued that this method is mathematically sound. Various examples are given (Michaelis-Menten mechanism, two-substrate mechanism, ...) and older related techniques from the 50-60ies are briefly discussed.

home