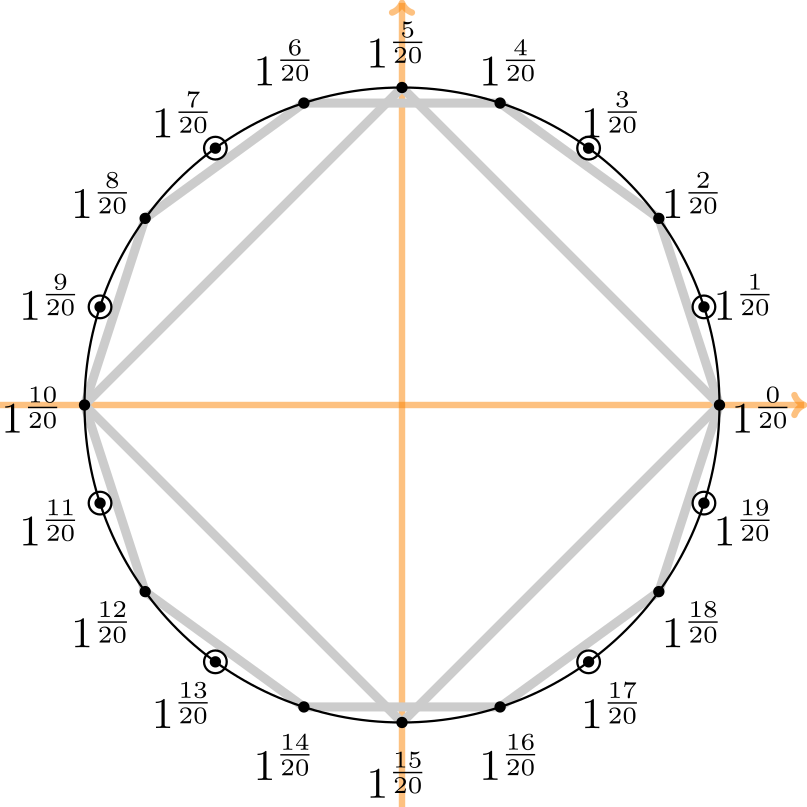
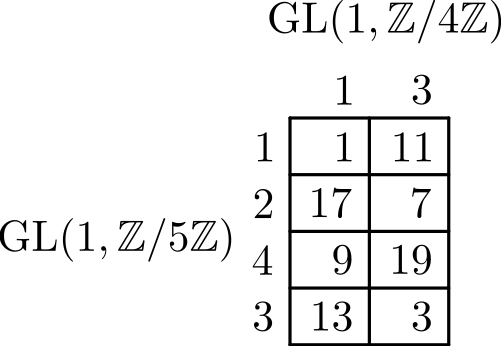
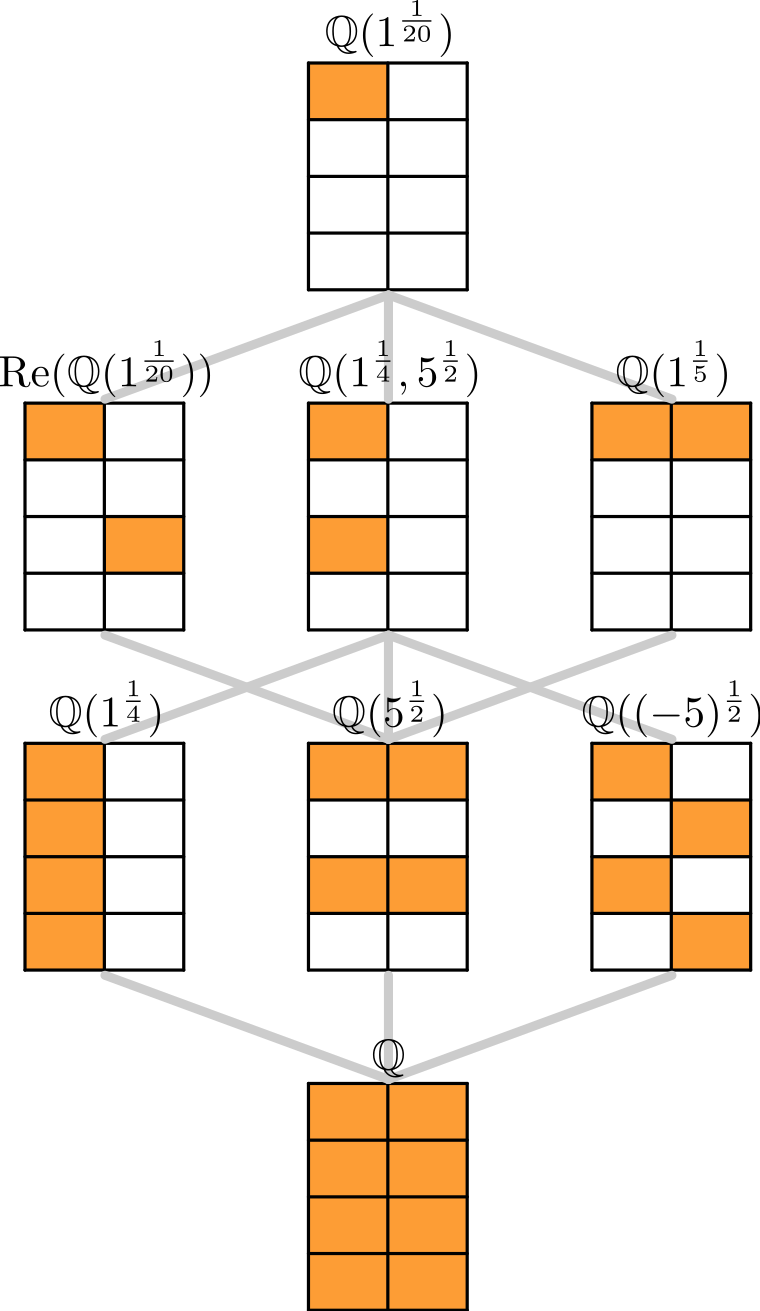
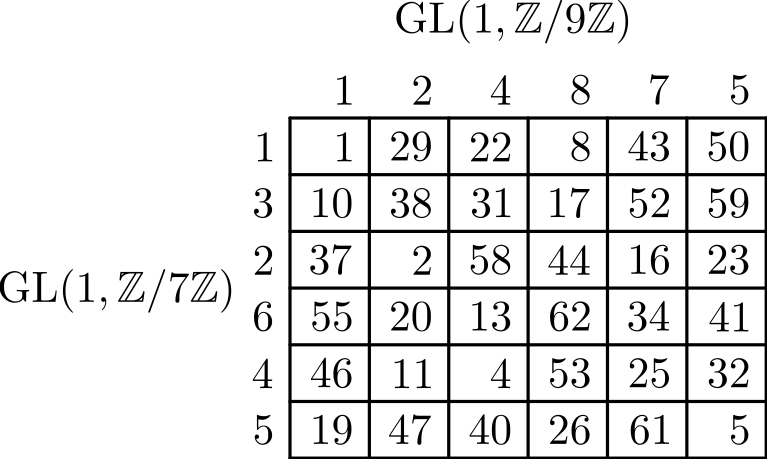
An attempt to understand some of James Dolan's recent thoughts on
torsors. Fix a field \(k\) and a finite group \(G\). Let
\(\mathrm{Vect}\) be the category of vector spaces over \(k\). Let
\(\mathrm{Rep}(G)\) be the category of representations of G on vector
spaces over k. \(\mathrm{Rep}(G)\) is a '2-rig', or more precisely a
locally presentable 2-rig: that is, a symmetric monoidal locally
presentable Vect-enriched category.
\(\mathrm{Rep}(G)\) is generated, as a 2-rig, by the regular
representation of G, which we could call \(r(G)\). But
\(\mathrm{Rep}(G)\) also contains another special object \(k^G\): the
algebra of functions on the finite set \(G\), treated as a trivial
representation of \(G\). This is a coalgebra in \(\mathrm{Rep}(G)\)
whose comultiplication encodes the multiplication in \(G\). This
coalgebra \(k^G\) has a coaction on \(r(G)\), \(r(G) \to r(G) \otimes
k^G\). This coaction makes \(r(G)\) into what James calls a
'\(G\)-torsor in \(\mathrm{Rep}(G)\)', meaning that there is also a
'codivision' map \(k^G \to r(G) \otimes r(G)\) obeying a certain
equation. All this is dual to how a nonempty set \(X\) is a torsor of \(G\)
if it has an action \(G \times X \to X\) together with a division map
\(X \times X \to G\) obeying a certain equation.
Indeed, any 2-rig \(R\) contains a Hopf object that we could call
\(k^G\): it's the direct sum of \(G\) copies of the unit object, with
a comultiplication coming from multiplication in \(G\). We can use
this to define a concept of a '\(G\)-torsor in R', copying the definition
just given in \(\mathrm{Rep}(G)\).
Such a \(G\)-torsor in a 2-rig \(R\) works out to be the secretly the
same thing as a 2-rig map \(F \colon \mathrm{Rep}(G) \to R\) since we
can determine such an \(F\) by choosing any \(G\)-torsor in \(R\), and
vice versa. Thus, James usually shortcuts the whole process and
defines a \(G\)-torsor in a 2-rig \(R\) simply to be a 2-rig map \(F
\colon \mathrm{Rep}(G) \to R\).
Finally, suppose \(L\) is any field extending \(k\) with Galois group \(G\).
Then \(L\) gives an algebra object in \(\mathrm{Vect}\) which is also a
\(G\)-torsor in \(\mathrm{Vect}\).