This Week's Finds       Fun Stuff     Serious Stuff     Talks     Seminar     Diary     Blog      Mathstodon      YouTube      n-Category Café      Visual Insight      Physics FAQ    


Search the web Search my webpages

John Baez’s Stuff

I'm a mathematical physicist. I use category theory to study networks and help researchers use them in scientific software, such as quickly adaptable models of infectious disease. I'm also working on categorified ring theory, which sheds new light on topics such as Schur functors, plethysm, and the splitting principle. I explain math and physics on my blog, Mastodon, and my column in the Notices of the American Mathematical Society.

I am not taking new students at this time.

What's on This Site

Also try my blogging here:

For common questions about physics, you can't beat this:

I don't maintain this Physics FAQ - Don Koks does, so please send any comments about it to him, not me!

If reading my stuff makes you want to ask questions, take a look at this.

What’s New?


Six random permutations of a 500-element set, where
circle areas are drawn in proportion to cycle lengths.
From Analytic Combinatorics by Flajolet and Sedgewick.

I've got a new article on random permutations, the latest in a series about how to understand the statistics of random permutations using a blend of combinatorics, category theory, and even complex analysis!

Check out my new book! Click here to see it:

I've also got a course on applied category theory you can try. But my main work these days is using categories to make better software for modeling:

Check out this talk about two of my favorite numbers: 8 and 24.

I'm turning my old column into free books. You can get 3 here:

I gave a talk called "Shannon entropy from category theory" at the Tutorial on Categorical Semantics of Entropy. You can see a video or slides of my talk here.

I gave a colloquium at the Perimeter Institute on Fisher's fundamental theorem of natural selection. You can watch the video and also read my paper on this.

Also try my talk on Classical mechanics versus thermodynamics, where I explain the eerie similarity between Hamilton's equations and the Maxwell relations.

If you think fundamental physics is stuck, read my article on the joy of condensed matter physics.

Can we actually remove carbon dioxide from the air? Yes! Can we remove enough to make a difference? Yes! But what are the best ways, and how much can they accomplish? I explained that in my article in Nautilus, an online science magazine.


Read my pop article on algebraic geometry and geometric quantization: The math that takes Newton into the quantum world. And for more of the technical details, read this.

Check out this interview: A quest for beauty and clear thinking. Also check out my talk on Unsolved mysteries of fundamental physics, which is now available on video.

And while you're at it: take a copy of my diary from 2003 to July 2020!

Together with three students at Applied Category Theory 2018, I wrote a paper on biochemical coupling through emergent conservation laws. Try our blog posts about this!

Learn about quantum mechanics and the dodecahedron:

Then read about the glories of the 600-cell (Part 1, Part 2, Part 3), which is a 4-dimensional analogue of the icosahedron:

These posts lead up to a grand conclusion: the Kepler problem and the 600-cell!

And while you're at it, check out my new paper on the icosahedron and E8, and learn about excitonium, Wigner crystals, the universal snake-like continuum, and the connection between braids, entropy and the golden ratio!

Learn about diamondoids and phosphorus sulfides:

Check out my introduction to Kolmogorov complexity and related ideas:

Learn what Kosterlitz and Thouless did to win the 2016 physics Nobel Prize.

Try my articles on 'struggles with the continuum' — that is, problems with infinities in physics arising from our assumption that spacetime is a continuum:

Read about 'topological crystals':

Take a road trip to infinity:

There's a mysterious relation between the discriminant of the icosahedral group:

and the involutes of the cubic parabola:

Learn a bit about quantum gravity, n-categories, crackpots and climate change in my interview on Physics Forums.

Anita Chowdry and I gave a joint lecture on The Harmonograph at the University of Waterloo. You can watch a video of it!

Read the tale of a doomed galaxy:

or if you prefer, read about the mysteries of the inverse cube force law:

Then learn about the butterfly, the gyroid and the neutrino:

Nature and the world of human technology are full of networks. People like to draw diagrams of networks: flow charts, electrical circuit diagrams, signal-flow graphs, Bayesian networks, Feynman diagrams and the like. Mathematically minded people know that in principle these diagrams fit into a common framework: category theory. But we are still far from a unified theory of networks! Learn more here:

• Network Theory: overview. Video on YouTube.

• Network Theory I: electrical circuits and signal-flow graphs. Video on YouTube.

• Network Theory II: stochastic Petri nets, chemical reaction networks and Feynman diagrams. Video on YouTube.

• Network Theory III: Bayesian networks, information and entropy. Video on YouTube.

Last year I gave talks on What Is Climate Change and What To Do About It? at the Balsillie School of International Affairs. You can see the slides.

But if you prefer biology and algebraic topology, try my talk on Operads and the Tree of Life.

For fun, I've been continuing to study the octonions, E8, the exceptional Jordan algebra, the Leech lattice and related structures:

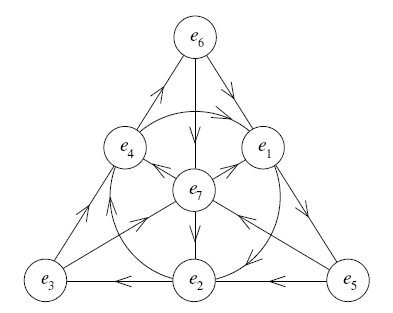
I also love Coxeter theory. Here's the Coxeter complex for the symmetry group of a dodecahedron:

You can learn more about this in my series "Platonic solids and the fourth dimension": part 1, part 2, part 3, part 4, part 5, part 6, part 7, part 8, part 9, part 10, part 11, part 12, and part 13.

Douglas Adams said the answer to life, the universe and everything is 42. But you may not know why. Now I have found out. The answer is related to Egyptian fractions and Archimedean tilings.

You may enjoy kaleidocycles and collidocycles:

Click the boxes to hear and read about some pieces I made with Greg Egan's QuasiMusic program, which translates quasicrystals into sound:

Read my series on the mathematical delights of rolling circles and balls!

There's a math puzzle whose answer is a really huge number. How huge? According to Harvey Friedman, it's incomprehensibly huge. Now Friedman is an expert on enormous infinite numbers and how their existence affects ordinary math. So when he says a finite number is incomprehensibly huge, that's scary. It's like seeing a seasoned tiger hunter running through the jungle with his shotgun, yelling "Help! It's a giant ant!" For more, read this.

In week319 of This Week's Finds, learn about catastrophe theory in climate physics! This issue features a program you can play with on your browser. It's a simple climate model that illustrates how a small increase in the amount of sunlight hitting the Earth could have a big effects on the climate, by melting snow and revealing darker soil. It was made by Allan Erskine.

Also on my blog, learn about ice, its many forms and crystal structures, how it resembles diamonds, and what scientists do with a machine that uses 80 times the world's electrical power for the few nanoseconds it's running.



< /div>



The universe is full of magical things, patiently waiting for our wits to grow sharper. - Eden Philpotts

© 2013 John Baez
baez@math.removethis.ucr.andthis.edu