Seminar - Fall 2016
Linear Algebraic Groups
John Baez
Here are the notes from a course on linear algebraic groups.
If you discover any errors in the notes please email me, and I'll
add them to the list of errors.
John Simanyi took notes in LaTeX, and you can see this
LaTeX files here.
-
Lecture 1 (Sept. 22) - The
definition of a linear algebraic group. Examples: the general linear
group \(\mathrm{GL}(n)\), the special linear group \(\mathrm{SL}(n)\),
the orthogonal group \(\mathrm{O}(n)\), the special orthogonal group
\(\mathrm{SO}(n)\), and the Euclidean group \(\mathrm{E}(n)\). The
origin of groups in geometry: the parallel postulate and Euclidean
versus non-Euclidean geometry. Elliptic and hyperbolic geometry.
-
Lecture 2 (Sept. 27) - The road to
projective geometry. Treating Euclidean, elliptic and hyperbolic
geometry on an equal footing: in each case the symmetry group is a
linear algebraic group of 3 × 3 matrices over a field \(k\),
points are certain 1d subspaces of \(k^3\), and lines are certain 2d
subspaces of \(k^3\). In projective geometry we take the symmetry
group to be all of \(\mathrm{GL}(3)\), take points to be
all 1d subspaces of \(k^3\), and take lines to be all 2d
subspaces of \(k^3\). It thus subsumes Euclidean, elliptic and
hyperbolic geometry. In general we define projective \(n\)-space,
\(k\mathrm{P}^n\), to be the set of 1d subspaces of \(k^{n+1}\).
-
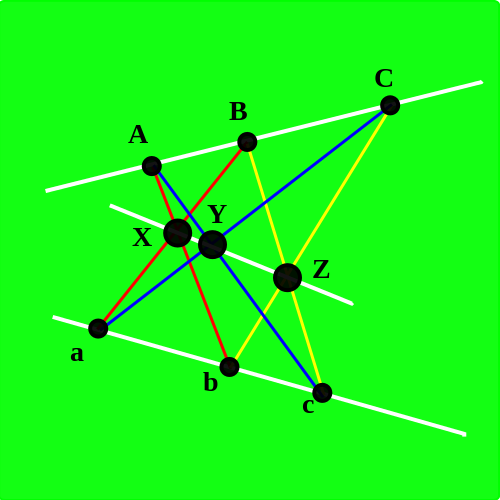
Lecture 3 (Sept. 29) - The Schubert
decomposition of \(k\mathrm{P}^n\) into Bruhat cells. Examples: the
real projective line \(\mathbb{R}\mathrm{P}^1\), the complex
projective plane \(\mathbb{C}\mathrm{P}^1\) and the real projective
plane \(\mathbb{R}\mathrm{P}^2\). Projective geometry over finite
fields: for any prime power \(q\), there is a field \(\mathbb{F}_q\)
with \(q\) elements, and the cardinality of
\(\mathbb{F}_q\mathrm{P}^n\) is the \(q\)-integer \([n]_q\). Abstract
projective planes.
-
Lecture 4 (Oct. 4) - Pappus's hexagon
theorem, and how it characterizes which abstract projective planes are
of the form \(k\mathrm{P}^2\) for a field \(k\). Klein geometry
and transitive group actions: each kind of highly symmetrical geometry
corresponds to a group \(G\), and each type of geometrical figure in this
geometry corresponds to a set on which \(G\) acts transitively.
Transitive \(G\)-spaces all arise from subgroups of \(G\). Klein geometry
studies invariant relations between transitive \(G\)-spaces.
Supplementary reading:
-
Lecture 5 (Oct. 6) - Projective
geometry from a Kleinian perspective. The Grassmannians
\(\mathrm{Gr}(n,j)\) as spaces of points, lines, planes, etc. in
projective geometry. The Grassmannians as quotients of the general
linear group by the maximal parabolic subgroups \(P_{n,j}\). Claim:
the cardinality of \(\mathrm{Gr}(n,j)\) over the finite field
\(\mathbb{F}_q\) is the \(q\)-binomial coefficient \(\binom{n}{j}_q\).
The mysterious sense in which set theory is linear algebra over the
'field with one element'.
-
Lecture 6 (Oct. 11) - Proof that
the cardinality of \(\mathrm{Gr}(n,j)\) over \(\mathbb{F}_q\) is
\(\binom{n}{j}_q\). The \(q\)-deformed version of Pascal's triangle.
Bruhat cells for the Grassmanian. How to count the total number of Bruhat
cells, which is just \(\binom{n}{j}\), and the number of cells of any
given dimension.
-
Lecture 7 (Oct. 13) - Flags, and the
the flag variety \(F(n_1, \dots, n_\ell, n)\), which consists of all
chains of linear subspaces \( V_1 \subset V_2 \subset \cdots \subset
V_\ell \subset k^n\). The flag variety as a quotients of the general
linear group by parabolic subgroups, which are intersections of
maximal parabolic subgroups. The complete flag variety \(F_n =
F(1,2,\dots,n)\) as the quotient \(GL(n)/B(n)\) where the Borel subgroup
\(B(n)\) is the group of invertible upper triangular matrices. The
cardinality of the
complete flag variety over \(\mathbb{F}_q\) is the \(q\)-factorial
\([n]_q!\). When \(q = 1\) this reduces to the ordinary factorial,
which counts 'set-theoretic flags'.
-
Lecture 8 (Oct. 18) - Group objects
in various categories. What's the
right category for linear algebraic groups? First try: algebraic
sets. Over an algebraically complete field \(k\), Hilbert's
Nullstellensatz says there's an order-reversing one-to-one
correspondence between algebraic sets \(S \subseteq X\) in a
finite-dimensional vector space \(X\) over \(k\) and radical ideals
\(J \subseteq k[X]\) of the polynomial algebra \(k[X]\). The algebra
\(k[S]\) of polynomials restricted to \(S\) is isomorphic to \(k[X]/J\).
Problem: we'd like an 'intrinsic' approach that does not make use of
the ambient space \(X\). Second try: affine algebras. For any
algebraic set \(S\), the algebra \(k[S]\) is an affine algebra,
meaning a finite-generated commutative algebra without nilpotents. Up
to isomorphism, every affine algebra arises this way. Thus we can use
affine algebras as a more intrinsic substitute for algebraic sets.
Problem: all this works only over an algebraically complete field.
Supplementary reading:
-
Lecture 9 (Oct. 20) -
The category \(\mathrm{AlgSet}_k\) of algebraic
sets and regular functions versus the category \(\mathrm{AffAlg}_k\)
of affine algebras and algebra homomorphisms. The duality between
geometry and commutative algebra: when \(k\) is algebraically closed,
\(\mathrm{AlgSet}_k \simeq \mathrm{AffAlg}_k^{\mathrm{op}}\).
We can define the category of affine varieties over \(k\),
\(\mathrm{AffVar}_k\), to be \(\mathrm{AffAlg}_k^{\mathrm{op}}\). Problems:
1) all this works only when \(k\) is algebraically closed, 2) it excludes
infinite-dimensional spaces corresponding to algebras that aren't
finitely generated, and 3) it excludes 'infinitesimal' spaces corresponding
to algebras with nilpotents. Third try: affine schemes. Grothendieck
simply defined the category of affine schemes over \(k\),
\(\mathrm{AffSch}_k\), to be the opposite of the category of commutative
algebras over \(k\).
Supplementary reading:
Lecture 10 (Oct. 25) - Affine algebraic
groups and affine algebraic group schemes.
Supplementary reading:
Lecture 11 (Oct. 27) - The big
theorem on Bruhat decompositions for reductive algebraic groups.
Lecture 12 (Nov. 1) - Illustrating
the big theorem on Bruhat decompositions: the case of \(\mathrm{GL}(3)\).
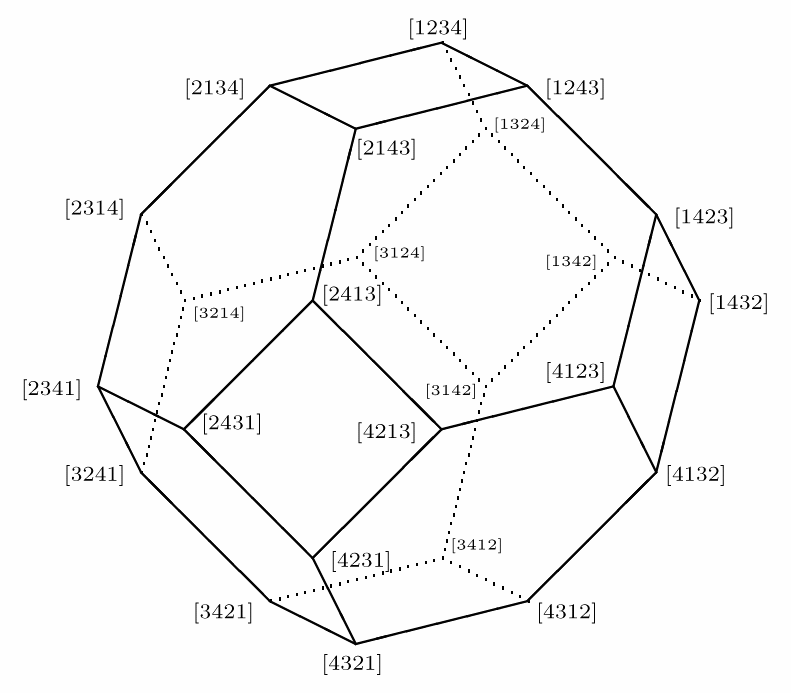
Lecture 13 (Nov. 3) -
Illustrating the big theorem on Bruhat decompositions: the case of
\(\mathrm{GL}(n)\). Permutahedra.
baez@math.removethis.ucr.andthis.edu
© 2016 John Baez