Two of My Favorite Numbers: 8 and 24

The numbers 8 and 24 play special roles in mathematics. The number 8 is special because of Bott periodicity, the octonions and the E8 lattice, while 24 is special for many reasons, including the binary tetrahedral group, the Dedekind eta function, the Leech lattice, and the third stable homotopy group of spheres. The number 8 does for superstring theory what the number 24 does for bosonic string theory. In this talk, which is intended to be entertaining, I will overview some of these matters and also some intriguing connections between the numbers 8 and 24.

• Wednesday August 2, 2023 - At 9:30 am Eastern Time I gave a talk at Applied Category Theory 2023:

  Software for Compositional Modeling in Epidemiology

  Mathematical models of disease are important and widely used, but building and working with these models at scale is challenging. Many epidemiologists use “stock and flow diagrams” to describe ordinary differential equation (ODE) models of disease dynamics. In this talk we describe and demonstrate two software tools for working with such models. The first, called StockFlow.jl, is based on category theory and written in AlgebraicJulia. The second, called ModelCollab, runs on a web browser and serves as a graphical user interface for StockFlow.jl. Modelers often regard diagrams as an informal step toward a mathematically rigorous formulation of a model in terms of ODEs. However, stock and flow diagrams have a precise mathematical syntax. Formulating this syntax using category theory has many advantages for software, but in this talk we explain three: functorial semantics, model composition, and model stratification. This is joint work with Xiaoyan Li, Sophie Libkind, Nathaniel Osgood, Evan Patterson and Eric Redekopp.

• Thursday August 24, 2023 - Juven Wang invited me to give a Zoom seminar on the numbers 8 and 24 on August 24th, 8/24. My talk started at 10 am Eastern Time, which is 3 pm here in the UK. He wrote: "This talk can be a research-level or intermediate-advanced-level talk (not colloquium) for postdocs, grads, and professors in math, mathematical physics, high-energy physics, or condensed matter physics. This talk can be an extension of your previous talks on the numbers 8 and 24. This will be part of Quantum Matter in Mathematics and Physics (QMMP)."

  Two of My Favorite Numbers: 8 and 24

  The numbers 8 and 24 play special roles in mathematics. The number 8 is special because of Bott periodicity, the octonions and the E8 lattice, while 24 is special for many reasons, including the binary tetrahedral group, the 3rd stable homotopy group of spheres, and the Leech lattice. The number 8 does for superstring theory what the number 24 does for bosonic string theory. In this talk, which is intended to be entertaining, I will overview these matters and also some connections between the numbers 8 and 24.

• Tuesday September 26, 2023 - at 6 pm I gave my second Leverhulme Lecture at the University of Edinburgh in room G.03 Bayes:

  Life's Struggle to Survive

  When pondering our future amid global warming, it is worth remembering how we got here. Even after it got started, the success of life on Earth was not a foregone conclusion! In this talk I recount some thrilling, chilling episodes from the history of our planet. For example: our collision with the planet Theia, the "snowball Earth events" when most of the oceans froze over, and the asteroid impact that ended the age of dinosaurs. Some are well-documented, others only theorized, but pondering them may give us some optimism about the ability of life to survive crises.

• Wednesday October 4, 2023 - at noon I gave a talk at the Edinburgh Category Theory Seminar.

  Schur Functors

  The representation theory of the symmetric groups is clarified by thinking of all representations of all these groups as objects of a single category: the category of Schur functors. These play a universal role in representation theory, since Schur functors act on the category of representations of any group. We can understand this as an example of categorification. A "rig" is a "ring without negatives", and the free rig on one generator is \(\mathbb{N}[x]\), the rig of polynomials with natural number coefficients. Categorifying the concept of commutative rig we obtain the concept of "symmetric 2-rig", and it turns out that the category of Schur functors is the free symmetric 2-rig on one generator. Thus, in a certain sense, Schur functors are the next step after polynomials.

• Wednesday October 18, 2023 - Jamie Vicary invited me to speak in the Logic and Semantics Seminar at the University of Cambridge. I spoke 2 to 3 pm in room LT1 of the Computer Laboratory. Lisa stayed in the Rylands Suite at Queens' College from Tuesday the 17th to Monday the 23rd, though I took a side-trip to Birmingham.

  Software for Compositional Modeling

  Mathematical models of disease are important and widely used, but building and working with these models at scale is challenging. Many epidemiologists use “stock and flow diagrams” to describe ordinary differential equation (ODE) models of disease dynamics. This talk introduces the mathematics of stock and flow diagrams and two software tools for working with them. The first, called StockFlow.jl, is based on category theory and written in AlgebraicJulia. The second, called ModelCollab, runs on a web browser and serves as a graphical user interface for StockFlow.jl. Modelers often regard diagrams as an informal step toward a mathematically rigorous formulation of a model in terms of ODEs. However, stock and flow diagrams have a precise mathematical syntax. Formulating this syntax using category theory has many advantages, but I will focus on three: functorial semantics, model composition, and model stratification. This is joint work with Xiaoyan Li, Sophie Libkind, Nathaniel Osgood, Evan Patterson and Eric Redekopp.

• Friday October 20, 2023 - at 11 am I spoke at the University of Birmingham's Theoretical Computer Science Seminar. I spoke in room LG12 of the Old Gym. My contact was George Kaye, with Martín Escardo serving as catalyst. I took a train from Cambridge to Birmingham on the 19th and had lunch and dinner with the computer scientists there. I stayed at the Edgbaston Park Hotel on campus and took a train back, with many delays and mishaps due to flooding.

  Software for Compositional Modeling

  Mathematical models of disease are important and widely used, but building and working with these models at scale is challenging. Many epidemiologists use “stock and flow diagrams” to describe ordinary differential equation (ODE) models of disease dynamics. This talk introduces the mathematics of stock and flow diagrams and two software tools for working with them. The first, called StockFlow.jl, is based on category theory and written in AlgebraicJulia. The second, called ModelCollab, runs on a web browser and serves as a graphical user interface for StockFlow.jl. Modelers often regard diagrams as an informal step toward a mathematically rigorous formulation of a model in terms of ODEs. However, stock and flow diagrams have a precise mathematical syntax. Formulating this syntax using category theory has many advantages, but I will focus on three: functorial semantics, model composition, and model stratification. This is joint work with Xiaoyan Li, Sophie Libkind, Nathaniel Osgood, Evan Patterson and Eric Redekopp.

• Tuesday November 14, 2023 - there was a meeting of TypeSig (the programming language theory student society in Edinburgh) from 6 pm to 8:30 pm in Lecture Theatre A at 40 George Square. From 7 to 8 pm I spoke about "What is Applied Category Theory?" based on my talk at David Corfield's Seminar on Applied Category Theory.

• Tuesday November 21, 2023 - at 6 pm I gave my third Leverhulme Lecture at the University of Edinburgh in room G.03 Bayes:

  The Answer to the Ultimate Question of Life, the Universe and Everything

  In The Hitchhiker's Guide to the Galaxy, by Douglas Adams, the number 42 was revealed to be the "Answer to the Ultimate Question of Life, the Universe, and Everything". But he didn't say what the question was! I will reveal that here. In fact it is a simple geometry question, which then turns out to be related to the mathematics underlying string theory.

• Wednesday November 29, 2023 - James Gaunt invited me to give an hour-long talk for math undergraduates at Heriot-Watt University as part of their Christmas Conference, a series of three talks. I again gave the above talk, The Answer to the Ultimate Question of Life, the Universe and Everything.

• Monday December 4, 2023 - Jules Hedges invited me to speak at CATNIP, the Categories Networking Project, at the University of Strathclyde.

  Software for Compositional Modeling

  Mathematical models of human interactions are important and widely used in epidemiology, but building and working with these models at scale is challenging. I will explain two software tools for doing this, both based on category theory. Modelers often regard diagrams as an informal step toward a mathematically rigorous formulation of a model. Giving these diagrams a precise syntax using category theory has many advantages, but I will focus on those connected to "community based modeling": the process of working with diverse community members to build a model. The next step is to tackle "agent-based models" and use them to help plan our response to climate change.

• Friday December 8, 2023 - At 4:30 pm I gave a talk at the Edinburgh Mathematical Society. My contact was Oana Pocovnicu, who wrote: "Prior to your talk, we'll have refreshments served from 4 pm at the Quad Café in the Law School, just along the corridor from the Usha Kasera Lecture Theatre. Here are some direction to the lecture theatre, in case they are useful. Enter the Old College quad from South Bridge (map). Head toward the grass, then turn right and enter the building using the entrance labelled “School of Law Reception”. Head for the Usha Kasera Lecture Theatre."

  Category Theory in Epidemiology

  "Stock and flow diagrams" are widely used for modeling in epidemiology.   Modelers often regard these diagrams as an informal step toward a mathematically rigorous formulation of a model in terms of ordinary differential equations.  However, these diagrams have a precise syntax, which can be explicated using category theory.  Although commercial tools already exist for drawing these diagrams and solving the differential equations they describe, my collaborators and I have created new software that overcomes some limitations of existing tools.   Basing this software on categories has many advantages, but I will explain three: functorial semantics, model composition, and model stratification.  This is joint work with Xiaoyan Li, Sophie Libkind, Nathaniel Osgood, Evan Patterson and Eric Redekopp.

Algorithmic Thermodynamics

Algorithmic entropy, as introduced by Kolmogorov, Chaitin and others, can be seen as a special case of entropy as studied in statistical mechanics. This viewpoint lets us apply ideas from thermodynamics to algorithmic information theory. For example, if we take the log runtime and length of a program as observables analogous to the energy \(E\) and volume \(V\) of a container of gas, the conjugate variables of these observables are quantities which we may call the algorithmic temperature \(T\) and algorithmic pressure \(P\), and an analogue of the fundamental thermodynamic relation \(dE = T dS - P dV\) holds. However, the resulting subject of "algorithmic thermodynamics" remains largely unexplored.

The Future of Physics

The 20th century was, arguably, the century of fundamental physics. While we saw immense progress on discovering the basic laws governing matter, space, and time, this has slowed to a crawl since 1980, despite an immense amount of work. But as I will explain, there is exciting progress in other branches of physics: for example, using the fundamental physics we already know to design surprising new forms of matter. Like all other sciences in the 21st century, physics must also embrace the challenges of the Anthropocene: the era in which humanity is a dominant influence on the Earth’s climate and biosphere.

The Tenfold Way

The importance of the tenfold way in physics was only recognized in this century. Simply put, it implies that there are ten fundamentally different kinds of matter. But it goes back to 1964, when the topologist C. T. C. Wall classified the associative real super division algebras and found ten of them. The three 'purely even' examples were already familiar: the real numbers, complex numbers and quaternions. The rest become important when we classify representations of groups on super Hilbert spaces. We explain this classification, its connection to Clifford algebras, and some of its implications for quantum physics.

The Tenfold Way

The importance of the tenfold way in physics was only recognized in this century. Simply put, it implies that there are ten fundamentally different kinds of matter. But it goes back to 1964, when the topologist C. T. C. Wall classified the associative real super division algebras and found ten of them. The three 'purely even' examples were already familiar: the real numbers, complex numbers and quaternions. The rest become important when we classify representations of groups on super Hilbert spaces. We explain this classification, its connection to Clifford algebras, and some of its implications for quantum physics.

The Tenfold Way

The importance of the tenfold way in physics was only recognized in this century. Simply put, it implies that there are ten fundamentally different kinds of matter. But it goes back to 1964, when the topologist C. T. C. Wall classified the associative real super division algebras and found ten of them. The three 'purely even' examples were already familiar: the real numbers, complex numbers and quaternions. The rest become important when we classify representations of groups on super Hilbert spaces. We explain this classification, its connection to Clifford algebras, and some of its implications for quantum physics.

The Tenfold Way

The importance of the tenfold way in physics was only recognized in this century. Simply put, it implies that there are ten fundamentally different kinds of matter. But it goes back to 1964, when the topologist C. T. C. Wall classified the associative real super division algebras and found ten of them. The three 'purely even' examples were already familiar: the real numbers, complex numbers and quaternions. The rest become important when we classify representations of groups on super Hilbert spaces. We explain this classification, its connection to Clifford algebras, and some of its implications for quantum physics.

• Friday September 9, 2022 - I spoke at 4 pm at GEOTOP-A, a web-seminar series on applications of geometry and topology. My hosts were José-Carlos Gómez-Larrañaga and Renzo L. Ricca.

  Compositional Modeling with Decorated Cospans

  One goal of applied category theory is to understand open systems: that is, systems with a boundary of some sort, through which matter, energy or information can flow in or out. We can describe a large class of open systems using the mathematics of decorated cospans, which we explain here. In various examples these ideas have been implemented in software. An interesting example comes from stock-flow diagrams, which are widely used in epidemiology to model the dynamics of populations. Although tools already exist for building these diagrams and simulating the systems they describe, we have created a new package called StockFlow which uses decorated cospans to overcome limitations of the existing tools. This is joint work with Xiaoyan Li, Sophie Libkind, Nathaniel Osgood and Evan Patterson.

• Tuesday September 27, 2022 - I spoke at 3 pm at the Edinburgh Statistical Physics and Complexity Webinar Series. My contacts were Martin Evans and Peter Mottishaw. I spoke on the fundamental theorem of natural selection.

  The Fundamental Theorem of Natural Selection

  In 1930, the famous statistician and geneticist Ronald Fisher claimed to have proved a "fundamental theorem of natural selection". He compared this result to the second law of thermodynamics, and described it as holding "the supreme position among the biological sciences". But others found it obscure, and in its most obvious interpretation it is simply false. Luckily there is a true result closely resembling Fisher's claim: a general theorem connecting dynamical systems and information theory. I'll explain this, give the very simple proof, and draw a few conclusions.

• Wednesday November 2, 2022 - I gave a talk at the African Mathematics Seminar at 15:00 - 16:00 East African Time, which is probably 12:00 - 13:00 in Edinburgh. My contact was Layla Sorkatti.

  Category Theory in Epidemiology

  Category theory provides a general framework for building models of dynamical systems. We explain this framework and illustrate it with the example of "stock and flow diagrams". These diagrams are widely used for simulations in epidemiology. Although tools already exist for drawing these diagrams and solving the systems of differential equations they describe, we have created a new software package called StockFlow which uses ideas from category theory to overcome some limitations of existing software. We illustrate this with code in StockFlow that implements a simplified version of a COVID-19 model used in Canada. This is joint work with Xiaoyan Li, Sophie Libkind, Nathaniel Osgood and Evan Patterson.

• Tuesday November 15, 2022 - I ran a seminar on "building online communities" in the mathematics department of the University of Edinburgh in the James Clerk Maxwell Building, room 4325A at 2-3 pm.
• Tuesday November 29, 2022 - At 6 pm UK time I gave the Leverhulme Lecture, a public talk at the International Centre of Mathematical Sciences.

  Mysteries of Fundamental Physics

  In this century, progress in fundamental physics has been slow. The Large Hadron Collider hasn't yet found any surprises, attempts to directly detect dark matter have been unsuccessful, string theory hasn't made any successful predictions, and nobody really knows what to do about any of this. But there is no shortage of problems, and clues. After a quick review of our best theories of physics so far — general relativity and the Standard Model — I will list some of the main open problems.

• Tuesday December 6, 2022 - At 11 am UK time I spoke at the Statistics and Data Science Seminar at Queen Mary University of London. I was invited by Nina Otter. I spent two nights in a hotel there, Monday December 5th and Tuesday December 6th, and I met Nina at 10:50 in the Mathematical Sciences Building on the Mile End campus, on the 5th floor near the seminar room (room MB503).

  Information Theory in Population Dynamics

  Information theory has interesting connections to the population dynamics of self-replicating entities. The relevant concept of information turns out to be the information of one probability distribution relative to another, also known as the Kullback–Liebler divergence. Using this we can get a new outlook on free energy, see evolution as a learning process, and give a clearer, more general formulation of Fisher's fundamental theorem of natural selection.

• Thursday December 8, 2022 - At 2:30 pm I spoke at the Logic and Semantics Seminar at University College London. My original contact was Fabio Zanasi, who writes "Besides me, the group hosts a few people that would be interested in your work, including Mehrnoosh Sadrzadeh, Samson Abramsky, my postdoc Robin Piedeleu, and a few of our PhD students who had ACT papers this year." Timo Lang booked me a room in the Grange Clarendon Hotel London for two nights: Wednesday December 7th and Thursday December 8th.

  Compositional Modeling with Decorated Cospans

  Decorated cospans are a general framework for working with open systems with the help of double categories. We explain this framework and illustrate it with the example of stock-flow diagrams. These diagrams are widely used in epidemiology to model the dynamics of populations. Although tools already exist for building these diagrams and simulating the models they describe, we have created a software package called StockFlow which uses decorated cospans to overcome some limitations of existing software. Our approach enables the composition of stock-flow diagrams, and cleanly separates their syntax from the semantics they can be assigned. We have implemented three forms of semantics, including one where stock-flow diagrams are mapped to ordinary differential equations. We have also created a web-based graphical user interface for StockFlow that requires no knowledge of category theory or programming to use. This is joint work with Xiaoyan Li, Sophie Libkind, Nathaniel Osgood, Evan Patterson, Long Pham and Eric Redekopp.

• Friday December 9, 2022 - At 4 pm I spoke in the Mathematics Colloquium at the University of Warwick. My contact was Adam Epstein, who wrote: "The 45-50 minute talks take place from 4 pm to 5 pm UK time on Fridays, currently in a hybrid format, online via MS Teams, and face-to-face if travel is congenial. The talks are followed by an optional informal wine and cheese social." Lisa and I then spent a night in a conference center on campus before taking a train first to London and then Edinburgh. Here's my talk abstract:

  Category Theory in Epidemiology

  Category theory provides a general framework for building models of dynamical systems. We explain this framework and illustrate it with the example of "stock and flow diagrams". These diagrams are widely used for simulations in epidemiology. Although tools already exist for drawing these diagrams and solving the systems of differential equations they describe, we have created a new software package called StockFlow which uses ideas from category theory to overcome some limitations of existing software. We illustrate this with code in StockFlow that implements a simplified version of a COVID-19 model used in Canada. This is joint work with Xiaoyan Li, Sophie Libkind, Nathaniel Osgood and Evan Patterson.

• Monday December 19 - Tuesday December 20, 2022 - Chris Heunen invited me to speak at SYCO10 in Edinburgh, and I gave this talk at 9:45-10:45 am on Tuesday:

  Compositional Modeling with Decorated Cospans

  Decorated cospans are a general framework for working with open systems with the help of double categories. We explain this framework and illustrate it with the example of stock-flow diagrams. These diagrams are widely used in epidemiology to model the dynamics of populations. Although tools already exist for building these diagrams and simulating the models they describe, we have created a software package called StockFlow which uses decorated cospans to overcome some limitations of existing software. Our approach enables the composition of stock-flow diagrams, and cleanly separates their syntax from the semantics they can be assigned. We have implemented three forms of semantics, including one where stock-flow diagrams are mapped to ordinary differential equations. We have also created a web-based graphical user interface for StockFlow that requires no knowledge of category theory or programming to use. This is joint work with Xiaoyan Li, Sophie Libkind, Nathaniel Osgood, Evan Patterson, Long Pham and Eric Redekopp.

Petri Nets as a Source of Mathematical Structures

A Petri net has a set of places, drawn here as circles, and a set of transitions, drawn as squares: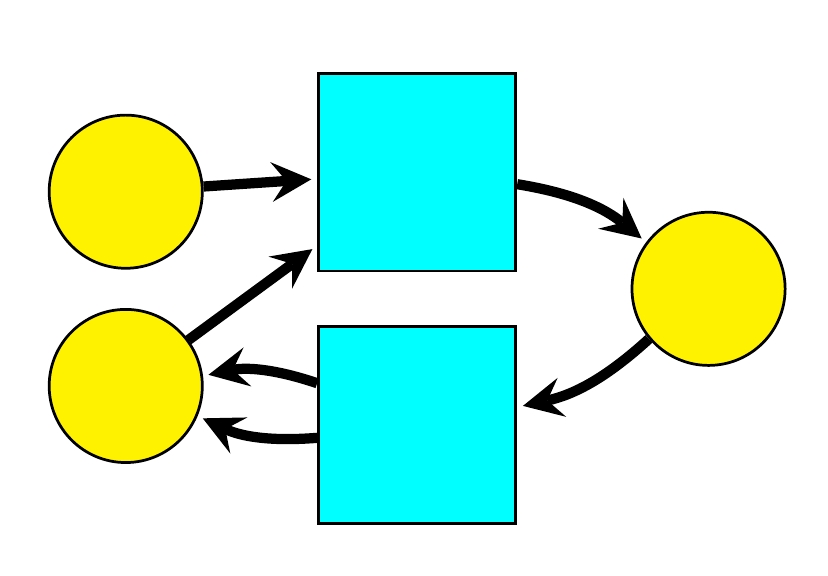

Each transition goes from a finite formal sum of places to a finite formal sum of places. Petri nets are used in computer science, chemistry and other disciplines to describe processes where finite collections of entities of different kinds turn into other such collections. Here we explore Petri nets as a source of interesting categories, monoids, posets and other structures.

Mathematically, a Petri net \(P\) can be seen as a way of presenting a free commutative monoidal category \(FP\): that is, commutative monoid object in \(\mathsf{Cat}\), which can be seen as symmetric monoidal category of an especially strict sort. We can then extract other structures from \(FP\). First, we can turn any category into a preorder, or by taking a skeleton, a poset. This process turns \(FP\) into partially ordered commutative monoid where \(x \le y\) iff there is a morphism in \(FP\) from the object \(x\) to the object \(y\). The question of explicitly computing this partial order for a finite Petri net is a famous problem in computer science: the "reachability problem".

Next, we can take any partially ordered commutative monoid and construct a commutative monoid by modding out by the smallest congruence containing \(\le\). This amounts to promoting inequalities to equations. Thus, Petri nets give presentations of commutative monoids.

Finally, given a partially ordered commutative monoid, we can form a commutative quantale. This can be seen as model of a fragment of linear logic where there are two notions of "and": a cartesian one and a noncartesian one. The interpretation of these in terms of "the logic of resources" is especially vivid for commutative quantales arising from Petri nets.

Structured Versus Decorated Cospans

One goal of applied category theory is to understand open systems in a compositional manner. We compare two ways of describing open systems as cospans equipped with extra data — structured and decorated cospans — and explain a generalization of Fong's original decorated cospans which allows the extra data to be an object in a category, rather than merely an element of a set. We state a sufficient condition for decorated cospans to be equivalent to structured cospans, and give applications to open Petri nets. We also discuss the question of when these constructions are not equivalent: this appears to be the case for open dynamical systems and perhaps open systems of chemical reactions.

Compositional Modeling with Stock-Flow Diagrams

Stock and flow diagrams are widely used in epidemiology to model the dynamics of populations. Although tools already exist for building these diagrams and simulating the systems they describe, we have created a new package called StockFlow, part of the AlgebraicJulia ecosystem, which uses ideas from category theory to overcome notable limitations of existing software. Compositionality is provided by the theory of decorated cospans: stock and flow diagrams can composed to form larger ones in an intuitive way formalized by the operad of undirected wiring diagrams. Our approach also cleanly separates the syntax of stock and flow diagrams from the semantics they can be assigned. We consider semantics in ordinary differential equations, although others are possible. As an example, we explain code in Stockflow that implements a simplified version of a COVID-19 model used in Canada.

Compositional Modeling with Decorated Cospans

Decorated cospans are a general framework for composing open networks and mapping them to dynamical systems. We explain this framework and illustrate it with the example of stock and flow diagrams. These diagrams are widely used in epidemiology to model the dynamics of populations. Although tools already exist for building these diagrams and simulating the systems they describe, we have created a new software package called StockFlow which uses decorated cospans to overcome some limitations of existing software. Our approach cleanly separates the syntax of stock and flow diagrams from the semantics they can be assigned. We have implemented a semantics where stock and flow diagrams are mapped to ordinary differential equations, although others are possible. We illustrate this with code in StockFlow that implements a simplified version of a COVID-19 model used in Canada. This is joint work with Xiaoyan Li, Sophie Libkind, Nathaniel Osgood and Evan Patterson.

Shannon Entropy from Category Theory

Shannon entropy is a powerful concept. But what properties single out Shannon entropy as special? Instead of focusing on the entropy of a probability measure on a finite set, it can help to focus on the "information loss", or change in entropy, associated with a measure-preserving function. Shannon entropy then gives the only concept of information loss that is functorial, convex-linear and continuous. This is joint work with Tom Leinster and Tobias Fritz.

It will be held at the the same time as an MRC on Data Science at the Crossroads of Analysis, Geometry, and Topology.

Applied category theory is an emerging field of study focused on the discovery and development of real-world applications of category theory. Until recently, category theory has been used as an abstract framework to relate structure underlying collections of mathematical objects and is used as such by algebraic geometers, homotopy theorists, and logicians. It is rapidly becoming clear that these features of category theory also make it an ideal framework with which to analyze systems of interest across disparate applied contexts. Recent examples include systems engineering, epidemiological models, database theory, distributed systems, and game theory. This MRC will provide a focused long-term agenda for early-career mathematicians in the US interested in applying category theoretic approaches to studying real-world problems. Applicants from academia and industry are welcome.

During the workshop, we intend to focus on three specific areas of application. John Baez (University of Riverside) will lead a study of chemical reaction networks using category theoretic methods. Valeria de Paiva (Topos Institute) will lead a study in the context of computer science by looking into indexed containers and partial compilers using lenses and Dialectica Categories. Nina Otter (Queen Mary University of London) will lead a study of social networks using simplicial complexes.

Motivating Motives

Underlying the Riemann Hypothesis there is a question whose full answer still eludes us: what do the zeros of the Riemann zeta function really mean? As a step toward answering this, André Weil proposed a series of conjectures that include a simplified version of the Riemann Hypothesis in which the meaning of the zeros becomes somewhat easier to understand. Grothendieck and others worked for decades to prove Weil's conjectures, inventing a large chunk of modern algebraic geometry in the process. This quest, still in part unfulfilled, led Grothendieck to dream of "motives": mysterious building blocks that could explain the zeros (and poles) of Weil's analogue of the Riemann zeta function. This talk by a complete amateur will try to sketch some of these ideas in ways that other amateurs can enjoy.

Shannon Entropy from Category Theory

Shannon entropy is a powerful concept. But what properties single out Shannon entropy as special? Instead of focusing on the entropy of a probability measure on a finite set, it can help to focus on the "information loss", or change in entropy, associated with a measure-preserving function. Shannon entropy then gives the only concept of information loss that is functorial, convex-linear and continuous. This is joint work with Tom Leinster and Tobias Fritz.

Session Description: Since Lotka, physical scientists have argued that living things belong to a class of complex and orderly systems that exist not despite the second law of thermodynamics, but because of it. Life and evolution, through natural selection of dissipative structures, are based on non-equilibrium thermodynamics. The challenge is to develop an understanding of what the respective physical laws can tell us about flows of energy and matter in living systems, and about growth, death and selection. This session will address current challenges including understanding emergence, regulation and control across scales, and entropy production, from metabolism in microbes to evolving ecosystems.

Categories: the Mathematics of Connection

As we move from the paradigm of modeling one single self-contained system at a time to modeling 'open systems' which interact with their — perhaps unmodeled — environment, category theory becomes a useful tool. It gives a mathematical language to describe the interface between an open system and its environment, the process of composing open systems along their interfaces, and how the behavior of a composite system relates to the behaviors of its parts. It is far from a silver bullet: at present, every successful application of category theory to open systems takes hard work. But I believe we are starting to see real progress.

Schur functors

The representation theory of the symmetric groups is clarified by thinking of all representations of all these groups as objects of a single category: the category of Schur functors. These play a universal role in representation theory, since Schur functors act on the category of representations of any group. We can understand this as an example of categorification. A "rig" is a "ring without negatives", and the free rig on one generator is \(\mathbb{N}[x]\), the rig of polynomials with natural number coefficients. Categorifying the concept of commutative rig we obtain the concept of "symmetric 2-rig", and it turns out the category of Schur functors is the free symmetric 2-rig on one generator. Thus, in a certain sense, Schur functors are the next step after polynomials.

Visions for the Future of Physics

The 20th century was the century of fundamental physics. What about the 21st? Progress on fundamental physics has been slow since about 1980, but there is exciting progress in other fields, such as condensed matter physics. Most of all, physicists in the 21st century should embrace the challenges of the Anthropocene.

Classical Mechanics versus Thermodynamics

It came as a shock when I first realized that some of the most famous equations in thermodynamics are just the same as the most famous equations in classical mechanics — with only the names of the variables changed. It turns out that this follows from a deep and not yet thoroughly studied analogy between the two subjects, which I will explain.

The Fundamental Theorem of Natural Selection

In 1930, the famous statistician and geneticist Ronald Fisher claimed to have proved a "fundamental theorem of natural selection". He compared this result to the second law of thermodynamics, and described it as holding "the supreme position among the biological sciences". But others found it obscure, and in its most obvious interpretation it is simply false. Luckily there is a true result closely resembling Fisher's claim: a general theorem connecting dynamical systems and information theory. I'll explain this, give the very simple proof, and draw a few conclusions.

Theoretical Physics in the 21st Century

The 20th century was the century of physics. What about the 21st? Though progress on some old problems is frustratingly slow, exciting new questions are emerging in condensed matter physics, nonequilibrium thermodynamics and other fields. And most of all, the 21st century is the dawn of the Anthropocene, in which we will adapt to the realities of life on a finite-sized planet. How can physicists help here?

Structured vs Decorated Cospans

One goal of applied category theory is to understand open systems: that is, systems that can interact with the external world. We compare two approaches to describing open systems as morphisms: structured and decorated cospans. Each approach provides a symmetric monoidal double category. Structured cospans are easier, decorated cospans are more general, but under certain conditions the two approaches are equivalent. We take this opportunity to explain some tricky issues that have only recently been resolved.

The Answer to the Ultimate Question of Life, the Universe and Everything

In The Hitchhiker's Guide to the Galaxy, by Douglas Adams, the number 42 is revealed to be the "Answer to the Ultimate Question of Life, the Universe, and Everything". But he didn't say what the question was! I will reveal that here. In fact it is a simple geometry question, which turns out to be related to the mathematics underlying string theory.

Since Lotka, physical scientists have argued that living things belong to a class of complex and orderly systems that exist not despite the second law of thermodynamics, but because of it. Life and evolution, through natural selection of dissipative structures, are based on non-equilibrium thermodynamics. The challenge is to develop an understanding of what the respective physical laws can tell us about flows of energy and matter in living systems, and about growth, death and selection. This session will address current challenges including understanding emergence, regulation and control across scales, and entropy production, from metabolism in microbes to evolving ecosystems.

Structured versus Decorated Cospans

One goal of applied category theory is to understand open systems: that is, systems that can interact with the external world. We compare two approaches to describing open systems as cospans equipped with extra data: structured and decorated cospans. Each approach provides a symmetric monoidal double category, and we prove that under certain conditions these symmetric monoidal double categories are equivalent. We illustrate these ideas with applications to dynamical systems, such as modeling the spread of COVID-19. This is joint work with Kenny Courser and Christina Vasilakopoulou.

Symmetric Monoidal Categories: a Rosetta Stone

Scientists and engineers like to describe processes or systems made of smaller pieces using diagrams: flow charts, Petri nets, electrical circuit diagrams, signal-flow graphs, chemical reaction networks, Feynman diagrams and the like. Many of these diagrams fit into a common framework: the mathematics of symmetric monoidal categories. When we embrace this realization, we start seeing connections between seemingly different subjects. We also get better tools for understanding open systems: systems that interact with their environment. This takes us beyond the old scientific paradigm that emphasizes closed systems.

Can We Understand the Standard Model Using Octonions?

Dubois-Violette and Todorov have shown that the Standard Model gauge group can be constructed using the exceptional Jordan algebra, consisting of 3×3 self-adjoint matrices of octonions. After an introduction to the physics of Jordan algebras, we ponder the meaning of their construction. For example, it implies that the Standard Model gauge group consists of the symmetries of an octonionic qutrit that restrict to symmetries of an octonionic qubit and preserve all the structure arising from a choice of unit imaginary octonion. It also sheds light on why the Standard Model gauge group acts on 10d Euclidean space, or Minkowski spacetime, while preserving a 4+6 splitting.

The Answer to the Ultimate Question of Life, the Universe and Everything

In The Hitchhiker's Guide to the Galaxy, by Douglas Adams, the number 42 is revealed to be the "Answer to the Ultimate Question of Life, the Universe, and Everything". But he didn't say what the question was! I will reveal that here. In fact it is a simple geometry question, which turns out to be related to the mathematics underlying string theory.

Can We Understand the Standard Model?

40 years trying to go beyond the Standard Model hasn't yet led to any clear success. As an alternative, we could try to understand why the Standard Model is the way it is. In this first talk we review some lessons from grand unified theories and also from recent work using the octonions. The gauge group of the Standard Model and its representation on one generation of fermions arises naturally from a process that involves splitting 10d Euclidean space into 4+6 dimensions, but also from a process that involves splitting 10d Minkowski spacetime into 4d Minkowski space and 6 spacelike dimensions. We explain both these approaches, and how to reconcile them.

Mathematics in the 21st Century

The climate crisis is part of a bigger transformation in which humanity realizes that the Earth is a finite system and that no physical quantity can grow exponentially forever. This transformation may affect mathematics — and be affected by it — just as dramatically as the agricultural and industrial revolutions did. After a review of the problems, we discuss how mathematicians can help make this transformation a bit easier, and some ways in which mathematics may change.

Theoretical Physics in the 21st Century

The 20th century was the century of physics. What about the 21st? Though progress on some old problems is frustratingly slow, exciting new questions are emerging in condensed matter physics, nonequilibrium thermodynamics and other fields. And most of all, the 21st century is the dawn of the Anthropocene, in which we will adapt to the realities of life on a finite-sized planet. How can physicists help here?

Structured versus Decorated Cospans

One goal of applied category theory is to understand open systems: that is, systems that can interact with the external world. We compare two approaches to describing open systems as cospans equipped with extra data: structured and decorated cospans. Each approach provides a symmetric monoidal double category, and we prove that under certain conditions these symmetric monoidal double categories are equivalent. We illustrate these ideas with applications to dynamical systems, such as modeling the spread of COVID-19. This is joint work with Kenny Courser and Christina Vasilakopoulou.

Ramanujan's Easiest Formula

A while ago I decided to figure out how to prove one of Ramanujan’s formulas. I feel this is the sort of thing every mathematician should try at least once. I picked the easiest one I could find. Hardy called it one of the “least impressive". Still, it was pretty interesting: it turned out to be a puzzle within a puzzle! It has an easy outer layer which one can solve using standard ideas in calculus, and a tougher inner core which requires more cleverness.

Schur Functors

The representation theory of the symmetric groups is clarified by thinking of all representations of all these groups as objects of a single category: the category of Schur functors. These play a universal role in representation theory, since Schur functors act on the category of representations of any group. We can understand this as an example of categorification. A "rig" is a "ring without negatives", and the free rig on one generator is N[x], the rig of polynomials with natural number coefficients. Categorifying the concept of commutative rig we obtain the concept of "symmetric 2-rig". Here we show that the category of Schur functors is the free symmetric 2-rig on one generator.

Fock Space Techniques for Stochastic Physics

Some ideas from quantum theory are beginning to percolate back to classical probability theory. For example, the master equation for a chemical reaction network — also known as a stochastic Petri net — describes particle interactions in a stochastic rather than quantum way. If we look at this equation from the perspective of quantum theory, this formalism turns out to involve creation and annihilation operators, coherent states and other well-known ideas — but with a few big differences.

Coarse-Graining Open Markov Processes

We illustrate some new paradigms in applied category theory with the example of coarse-graining open Markov processes. Coarse-graining is a standard method of extracting a simpler Markov process from a more complicated one by identifying states. Here we extend coarse-graining to 'open' Markov processes: that is, those where probability can flow in or out of certain states called 'inputs' and 'outputs'. One can build up an ordinary Markov process from smaller open pieces in two basic ways: composition, where we identify the outputs of one open Markov process with the inputs of another, and tensoring, where we set two open Markov processes side by side. These constructions make open Markov processes into the morphisms of a symmetric monoidal category. But we can go further and construct a symmetric monoidal double category where the 2-morphisms include ways of coarse-graining open Markov processes. We can describe the behavior of open Markov processes using double functors out of this double category.

Structured Cospans and Open Petri Nets

“Structured cospans” are a general way to study networks with inputs and outputs. Here we illustrate this using a type of network popular in theoretical computer science: Petri nets. An “open” Petri net is one with certain places designated as inputs and outputs. We can compose open Petri nets by gluing the outputs of one to the inputs of another. Using the formalism of structured cospans, open Petri nets can be treated as morphisms of a symmetric monoidal category — or better, a symmetric monoidal double category. We explain two forms of semantics for open Petri nets using symmetric monoidal double functors out of this double category. The first, an operational semantics, gives for each open Petri net a category whose morphisms are the processes that this net can carry out. The second, a “reachability” semantics, simply says what these processes can accomplish.

Structured Cospans and Double Categories

One goal of applied category theory is to better understand networks appearing throughout science and engineering. Here we introduce “structured cospans” as a way to study networks with inputs and outputs. Given a functor \(L \colon A \to X\), a structured cospan is a diagram in \(X\) of the form

$$ L(a) \to x \leftarrow L(b) $$

If \(A\) and \(X\) have finite colimits and \(L\) is a left adjoint, we obtain a symmetric monoidal category whose objects are those of \(A\) and whose morphisms are certain equivalence classes of structured cospans. However, this arises from a more fundamental structure: a symmetric monoidal double category where the horizontal 1-cells are structured cospans, not equivalence classes thereof. We explain the mathematics and illustrate it with an example from epidemiology.

From Classical to Quantum and Back

Edward Nelson famously claimed that quantization is a mystery, not a functor. In other words, starting from the phase space of a classical system (a symplectic manifold) there is no functorial way of constructing the correct Hilbert space for the corresponding quantum system. In geometric quantization one gets around this problem by equipping the classical phase space with extra structure: for example, a Kähler manifold equipped with a suitable line bundle. Then quantization becomes a functor. But there is also a functor going the other way, sending any Hilbert space to its projectivization. This makes quantum systems into specially well-behaved classical systems! In this talk we explore the interplay between classical mechanics and quantum mechanics revealed by these functors going both ways.

The audience will be undergraduate students (~25%), master’s graduate students (50%), and faculty (25%, I will invite both math and physics, but probably mostly physics faculty) and some physics-trained public attendees. It is a very diverse audience, so very few particle physics experts, and only a sub-group of general relativity experts, but those fields generally attract much interest. The presentation is about 45 minutes followed with 10-15 minutes of questions.

The colloquium starts at 11:15am after coffee time (10:45am), but we usually have speakers arrive around 9:45am - 10am to prepare and visit labs, etc.

Unsolved Mysteries of Fundamental Physics

In this century, progress in fundamental physics has been slow. The Large Hadron Collider hasn't yet found any surprises, attempts to directly detect dark matter have been unsuccessful, string theory hasn't made any successful predictions, and nobody really knows what to do about any of this. But there is no shortage of problems, and clues. Here we list a few.

Structured Cospans

Open systems of many kinds can be treated as morphisms in symmetric monoidal categories. Two complementary approaches can be used to work with such categories: props (which are more algebraic in flavor) and cospan categories (which are more geometrical). In this talk we focus on the latter. Brendan Fong's "decorated cospans" are a powerful tool for treating open systems as cospans equipped with extra structure. Recently Kenny Courser has found a simpler alternative, the theory of "structured cospans". We describe this theory and sketch how it has been applied to a variety of open systems, such as electrical circuits, Markov processes, chemical reactions and Petri nets.

Structured Cospans

Open systems of many kinds can be treated as morphisms in symmetric monoidal categories. Two complementary approaches can be used to work with such categories: props (which are more algebraic in flavor) and cospan categories (which are more geometrical). In this talk we focus on the latter. Brendan Fong's "decorated cospans" are a powerful tool for treating open systems as cospans equipped with extra structure. Recently Kenny Courser has found a simpler alternative, the theory of "structured cospans". We describe this theory and sketch how it has been applied to a variety of open systems, such as electrical circuits, Markov processes, chemical reactions and Petri nets.

Props in Network Theory

To describe systems composed of interacting parts, scientists and engineers draw diagrams of networks: flow charts, Petri nets, electrical circuit diagrams, signal-flow graphs, chemical reaction networks, Feynman diagrams and the like. All these different diagrams fit into a common framework: the mathematics of symmetric monoidal categories. Two complementary approaches are presentations of props using generators and relations (which are more algebraic in flavor) and structured cospan categories (which are more geometrical). In this talk we focus on the former. A "prop" is a strict symmetric monoidal category whose objects are tensor powers of a single generating object. We will see that props are a flexible tool for describing many kinds of networks.

Young Diagrams

Young diagrams are simple combinatorial structures that show up in a myriad of applications. Among other things they classify conjugacy classes in symmetric groups, irreducible representations of symmetric groups, irreducible representations of the groups SL(n,F) for any field F of characteristic zero, and irreducible complex representations of the groups SU(n). All these facts are tightly connected, and the central idea is that Young diagrams are irreducible objects in the category of "Schur functors". These are functors that know how to act on the category of representations of any group, and other similar categories as well.

The Answer to the Ultimate Question of Life, the Universe, and Everything

In The Hitchhiker's Guide to the Galaxy, by Douglas Adams, the number 42 is revealed to be the "Answer to the Ultimate Question of Life, the Universe, and Everything". But he didn't say what the question was! I will reveal that here. In fact it is a simple geometry question, which turns out to be related to the mathematics underlying string theory.

Hidden Symmetries of the Hydrogen Atom

A classical particle moving in an inverse square central force, like a planet in the gravitational field of the Sun, moves in orbits that do not precess. This lack of precession, special to the inverse square force, indicates the presence of extra conserved quantities beyond the obvious ones. Thanks to Noether's theorem, these indicate the presence of extra symmetries. It turns out that not only rotations in 3 dimensions, but also in 4 dimensions, act as symmetries of this system. These extra symmetries are also present in the quantum version of the problem, where they explain some surprising features of the hydrogen atom. The quest to fully understand these symmetries leads to some fascinating mathematical adventures.

The second, a public talk, was on Tuesday at 6:30 pm:

Mathematical Mysteries of the Periodic Table

Why do atoms behave the way they do? Why do electrons form "shells", as seen in the Periodic Table? Why does the first shell hold 2 electrons, the second 8, and the third 18: twice the square numbers 1, 4 and 9? It took many years to solve these mysteries, and a lot of detective work in chemistry, physics — and ultimately, once the relevant laws of physics were known, mathematics. Other mysteries remain unsolved, like the mass of the heaviest possible element. Here we give a quick tour of these puzzles and some of their answers.

In conjunction with the designation of 2019 as the International Year of the Periodic Table, the Georgia Tech College of Sciences is planning a series of public lectures on the periodic table and its impact on each of the Schools in the College. The goal is to make people focus on the role of the periodic table and elements in science and technology, with the intended audience being the science-literate and science-interested public. Speakers must be engaging and must tailor talks for a nonexpert audience (perhaps along the lines of a Quanta Magazine article).

I'm hoping that the Georgia Tech School of Mathematics can contribute to this endeavor by hosting a talk on the interplay between mathematics (especially the representation theory of Lie groups) and the periodic table. The idea would be to explain — in a relatively non-technical way — Lie groups and their representations, and to discuss how (and perhaps why) the periods which occur in the periodic table are the dimensions of irreducible representations of SO(3). Maybe a little background on quantum mechanics would be helpful as well, including Wigner's idea that different types of elementary particles should correspond to irreducible representations of SO(3)...

Biology as Information Dynamics

If biology is the study of self-replicating entities, and we want to understand the role of information, it makes sense to see how information theory is connected to the 'replicator equation' — a simple model of population dynamics for self-replicating entities. The relevant concept of information turns out to be the information of one probability distribution relative to another, also known as the Kullback–Liebler divergence. Using this we can get a new outlook on free energy, see evolution as a learning process, and give a clearer, more general formulation of Fisher's fundamental theorem of natural selection.

Getting to the Bottom of Noether's Theorem

In her paper of 1918, Noether's theorem relating symmetries and conserved quantities was formulated in term of Lagrangian mechanics. But if we want to make the essence of this relation seem as self-evident as possible, we can turn to a formulation in term of Poisson brackets, which generalizes easily to quantum mechanics using commutators. This approach also gives a version of Noether's theorem for Markov processes. The key question then becomes: when, and why, do observables generate one-parameter groups of transformations? This question sheds light on why complex numbers show up in quantum mechanics.

I spoke on Wednesday the 6th from 10:30 to 11:30 am.

From Classical to Quantum and Back

Edward Nelson famously claimed that quantization is a mystery, not a functor. In other words, starting from the phase space of a classical system (a symplectic manifold) there is no functorial way of constructing the correct Hilbert space for the corresponding quantum system. In geometric quantization one gets around this problem by equipping the classical phase space with extra structure: for example, a Kähler manifold equipped with a suitable line bundle. Then quantization becomes a functor. But there is also a functor going the other way, sending any Hilbert space to its projectivization. This makes quantum systems into specially well-behaved classical systems! In this talk we explore the interplay between classical mechanics and quantum mechanics revealed by these functors going both ways.

• Wednesday October 3, 2018 - Joanna Lada invited me to speak at the Cambridge University Physics Society (CUPS) at 8 pm at the Bristol-Meyers Squibb lecture theater in the Chemistry Department on Lensfield Road. The talk was aimed at undergraduate students of physics and the general public. I went to dinner with my hosts before the talk, around 6 pm, and there was a wine reception afterward. I spent a night at Corpus Christi before giving a talk at DAMTP and heading down to London on Thursday afternoon.

  Unsolved Mysteries of Fundamental Physics

  In this century, progress in fundamental physics has been slow. The Large Hadron Collider hasn't yet found any surprises, attempts to directly detect dark matter have been unsuccessful, string theory hasn't made any successful predictions, and nobody really knows what to do about any of this. But there is no shortage of problems, and clues. Here we list a few.

• Thursday October 4, 2018 - Ron A. Reid-Edwards and Carl Turner invited me to speak at DAMTP in Cambridge at 1 pm. I met them for coffee and then went to lunch at the CMS cafe. After the talk I talked to Tim Gowers and the took a taxi to the train station and headed down to London.

  Getting to the Bottom of Noether's Theorem

  In her paper of 1918, Noether's theorem relating symmetries and conserved quantities was formulated in term of Lagrangian mechanics. But if we want to make the essence of this relation seem as self-evident as possible, we can turn to a formulation in term of Poisson brackets, which generalizes easily to quantum mechanics using commutators. This approach also gives a version of Noether's theorem for Markov processes. The key question then becomes: when, and why, do observables generate one-parameter groups of transformations? This question sheds light on why complex numbers show up in quantum mechanics.

• Friday October 5 - Sunday October 7, 2018 - Nicholas Teh and Bryan Roberts invited me to speak at Philosophy and Physics of Noether's Theorems: A Centenary Conference on the 1918 Work of Emmy Noether at Fischer Hall in London. I gave the last talk, 5:30-6:30 pm on Saturday the 6th:

  Getting to the Bottom of Noether's First Theorem

  In her paper of 1918, Noether's first theorem relating symmetries and conserved quantities was formulated in term of Lagrangian mechanics. But if we want to make the essence of this relation seem as self-evident as possible, we can turn to a formulation in term of Poisson brackets, which generalizes easily to quantum mechanics using commutators. This approach also gives a version of Noether's theorem for Markov processes. The key question then becomes: when, and why, do observables generate one-parameter groups of transformations? This question sheds light on why complex numbers show up in quantum mechanics.

  Here's a description of the conference:

  The conference is intended to bring together leading physicists, mathematicians, and historians and philosophers of physics to reflect on the enduring legacy of Noether's theorems. It is jointly sponsored by the University of Notre Dame, the LSE Centre for Philosophy of Natural and Social Sciences, the National Science Foundation, the British Society for the Philosophy of Science, and the John Templeton Foundation.

  We would be delighted if you could help make this meeting a success by discussing any aspect of Noether's theorems from the perspective of category theory.

  Other invited scholars include: Yvette Kosmann-Schwarzbach, Harvey Brown, Jeremy Butterfield, Ana Cannas da Silva, Anne Davis, Ruth Gregory, Owen Gwilliam, Rob Spekkens, Sabrina Paterski, David Tong, Tudor Ratiu, and Frank Wilczek. We would be pleased to reimburse your travel expenses as well as provide accommodation in London for three nights.

  In addition, Cambridge University Press has expressed interest in publishing the papers based on this conference in a volume commemorating the centennial of Noether's theorems.

On Friday September 14, Kuldip Singh invited me to give a talk jointly to the Centre for Quantum Technologies and the Physics Department of the National University of Singapore.

Getting to the Bottom of Noether's Theorem

In her paper of 1918, Noether's theorem relating symmetries and conserved quantities was formulated in term of Lagrangian mechanics. But if we want to make the essence of this relation seem as self-evident as possible, we can turn to a formulation in term of Poisson brackets, which generalizes easily to quantum mechanics using commutators. This approach also gives a version of Noether's theorem for Markov processes. The key question then becomes: when, and why, do observables generate one-parameter groups of transformations? This question sheds light on why complex numbers show up in quantum mechanics.

On May 4th I gave this talk:

Props in Network Theory

The challenge of global warming brings into clear view the need for improved integration between category theory and other fields. Among other things, we need categories to understand networks. To describe systems composed of interacting parts, scientists and engineers draw diagrams of networks: flow charts, Petri nets, electrical circuit diagrams, signal-flow graphs, chemical reaction networks, Feynman diagrams and the like. All these different diagrams fit into a common framework: the mathematics of symmetric monoidal categories. Two complementary approaches are presentations of props using generators and relations (which are more algebraic in flavor) and decorated cospan categories (which are more geometrical). In this talk we focus on the former.

The Mathematics of Networks

Nature and the world of human technology are full of networks. People like to draw diagrams of networks: flow charts, electrical circuit diagrams, chemical reaction networks, signal-flow graphs, Bayesian networks, food webs, Feynman diagrams and the like. Far from mere informal tools, many of these diagrammatic languages fit into a rigorous framework: category theory. I will explain a bit of how this works and discuss some applications.

Biology as Information Dynamics

If biology is the study of self-replicating entities, and we want to understand the role of information, it makes sense to see how information theory is connected to the 'replicator equation' — a simple model of population dynamics for self-replicating entities. The relevant concept of information turns out to be the information of one probability distribution relative to another, also known as the Kullback–Liebler divergence. Using this we can get a new outlook on free energy, see evolution as a learning process, and give a clearer, more general formulation of Fisher's fundamental theorem of natural selection.

• August 6-13, 2017 - I gave one of 12 plenary lectures at the Applied Algebraic Topology 2017 at Hokkaido University in Sapporo, Japan. My contacts are Ran Levi and Kathryn Hess. Other plenary lectures will include Tom Leinster, Dmitry Kozlov, Rob Ghrist, Vin de Silva, Dan Freed, and (probably) Robert Adler.

  I flew out at 20:50 on the 6th and arrived on the 7th. The conference is on the 8th to the 12th. I returned on the 13th, with my flight leaving at 10:30 am. The program is here. My talk was from 9 to 10 am on Tuesday August 8:

  The Rise and Spread of Algebraic Topology

  As algebraic topology becomes more important in applied mathematics it is worth looking back to see how this subject has changed our outlook on mathematics in general. When Noether moved from working with Betti numbers to homology groups, she forced a new outlook on topological invariants: namely, they are often functors, with two invariants counting as "the same" if they are naturally isomorphic. To formalize this it was necessary to invent categories, and to formalize the analogy between natural isomorphisms between functors and homotopies between maps it was necessary to invent 2-categories. These are just the first steps in the "homotopification" of mathematics, a trend in which algebra more and more comes to resemble topology, and ultimately abstract "spaces" (for example, homotopy types) are considered as fundamental as sets. It is natural to wonder whether topological data analysis is a step in the spread of these ideas into applied mathematics, and how the importance of "robustness" in applications will influence algebraic topology.

At 11 am on Wednesday June 21 I gave this talk to undergraduate science majors:

Tales of the Dodecahedron: from Pythagoras through Plato to Poincaré

The dodecahedron is a beautiful shape made of 12 regular pentagons. It doesn't occur in nature; it was invented by the Pythagoreans, and we first read of it in a text written by Plato. We shall see some of its many amazing properties: its relation to the Golden Ratio, its rotational symmetries — and best of all, how to use it to create a regular solid in 4 dimensions! Poincaré exploited this to invent a 3-dimensional space that disproved a conjecture he made. This led him to an improved version of his conjecture, which was proved in 2003 by the reclusive Russian mathematician Grigori Perelman.

Applied Category Theory

Nature and the world of human technology are full of networks. People like to draw diagrams of networks: flow charts, electrical circuit diagrams, signal-flow graphs, Bayesian networks, Feynman diagrams and the like. Mathematically minded people know that in principle these diagrams fit into a common framework: category theory. But we are still far from a unified theory of networks.

The Mathematics of Open Reaction Networks

To describe systems composed of interacting parts, scientists and engineers draw diagrams of networks: flow charts, electrical circuit diagrams, signal-flow graphs, Feynman diagrams and the like. In principle all these different diagrams fit into a common framework: the mathematics of monoidal categories. This has been known for some time. However, the details are more challenging, and ultimately more rewarding, than this basic insight. Here we explain how various applications of reaction networks and Petri nets fit into this framework.

• May 20, 2017 - at 10:50 I gave the plenary talk at the Annual General Meeting of the Hong Kong Mathematical Society, invited by Tong Yang, president of this society.

  The Dodecahedron, the Icosahedron and E₈

  The regular dodecahedron and icosahedron were not first found in nature: they were discovered by Greek mathematicians, and we first read of them in a text written by Plato. Felix Klein used them to solve the quintic equation. But this was just the first step toward a more remarkable discovery: they can be used to construct the Poincaré homology 3-sphere and the E₈ lattice, which last year was proved to give the densest packing of spheres in 8 dimensions. The story is a long and fascinating one, but we only sketch part of it.

The focus was on ways to identify and quantify biological complexity. The central question is whether the complexity of living systems displays distinctive and potentially quantifiable properties that enable one to unambiguously distinguish life from non-biological complex systems. The workshop took place close to the ASU Tempe campus on February 1-3. It started with a reception on the evening of Tuesday January 31 and finished with lunch on Friday. Questions included:

• What measures of complexity might be suited to capture the elusive concept of "being alive"?
• Can different categories of organisms (e.g. prokaryotic, eukaryotic, multicellular, cancer) be defined by the nature as well as the level of their complexity?
• What is the relationship between entropy and complexity and how does this play out in living organisms?
• Are there laws of nature governing how (biological) complexity evolves, to stand alongside the laws of physics?
• How might relevant measures of complexity inform our search for life on other worlds?

My talk was on Thursday February 2nd from 10:00 to 10:45:

Biology as Information Dynamics

If biology is the study of self-replicating entities, and we want to understand the role of information, it makes sense to see how information theory is connected to the 'replicator equation' — a simple model of population dynamics for self-replicating entities. The relevant concept of information turns out to be the information of one probability distribution relative to another, also known as the Kullback–Leibler divergence. Using this we can get a new outlook on free energy, see evolution as a learning process, and give a clean general formulation of Fisher's fundamental theorem of natural selection.

I gave the following talk on Tuesday December 6th from 9:30 to 10:30 am. At 4:15 the same day I led an hour-long discussion on compositionality.

Compositionality in Network Theory

To describe systems composed of interacting parts, scientists and engineers draw diagrams of networks: flow charts, Petri nets, electrical circuit diagrams, signal-flow graphs, chemical reaction networks, Feynman diagrams and the like. In principle all these different diagrams fit into a common framework: the mathematics of symmetric monoidal categories. This has been known for some time. However, the details are more challenging, and ultimately more rewarding, than this basic insight. Two complementary approaches are presentations of symmetric monoidal categories using generators and relations (which are more algebraic in flavor) and decorated cospan categories (which are more geometrical). In this talk we focus on the latter.

Monoidal Categories of Networks

Nature and the world of human technology are full of networks. People like to draw diagrams of networks: flow charts, electrical circuit diagrams, chemical reaction networks, signal-flow graphs, Bayesian networks, food webs, Feynman diagrams and the like. Far from mere informal tools, many of these diagrammatic languages fit into a rigorous framework: category theory. I will explain a bit of how this works and discuss some applications.

At 11:20 am on Wednesday November 16th I gave a tutorial on Kolmogorov complexity and its relation to Shannon information:

Computation and Thermodynamics

This talk is about the link between computation and entropy. I take the idea of a Turing machine for granted, but starting with that I explain recursive functions, the Church-Turing thesis, Kolomogorov complexity, the relation between Kolmogorov complexity and Shannon entropy, the uncomputability of Kolmogorov complexity, the 'complexity barrier', Levin's computable version of complexity, and finally my work with Mike Stay on algorithmic thermodynamics.

The Answer to the Ultimate Question of Life, the Universe, and Everything

In The Hitchhiker's Guide to the Galaxy, by Douglas Adams, the number 42 is revealed to be the "Answer to the Ultimate Question of Life, the Universe, and Everything". But he didn't say what the question was! I will reveal that here. In fact it is a simple geometry question, which turns out to be related to the mathematics underlying string theory.

My Favorite Number

The number 24 plays a central role in the mathematics of string theory, thanks to a series of "coincidences" that is just beginning to be understood. One of the first hints of this fact was Euler's bizarre "proof" that

1 + 2 + 3 + 4 + ··· = -1/12

which he obtained before Abel declared that "divergent series are the invention of the devil". Euler's formula can now be understood rigorously, and in physics it explains why bosonic strings work best in 26=24+2 dimensions. The fact that

1² + 2² + 3² + ··· + 24²

is a perfect square then sets up a curious link between string theory, the Leech lattice (the densest way to pack spheres in 24 dimensions) and a huge group called the Monster.

My flight arrived in Toronto Wednesday evening. I took Airways Transit to the Waterloo Hotel at 2 King St. North at the intersection of King and Erb in Waterloo.

On Thursday Linda Carson took me to East Campus Hall, to meet Anita and see how her harmonograph workshop was going. I hung around there we had dinner with Linda and Craig Kaplan.

On Friday morning I went to the pure mathematics department, and Pavlina Penk found an office for me. By 3 pm I made my way to the cookies at the William G. Davis Centre in room DC 1301, in time for my talk at 3:30 pm. This was a Pure Mathematics and Combinatorics & Optimization joint colloquium:

My Favorite Number

The number 24 plays a central role in mathematics thanks to a series of "coincidences" that is just beginning to be understood. One of the first hints of this fact was Euler's bizarre "proof" that

1 + 2 + 3 + 4 + … = -1/12

which he obtained before Abel declared that "divergent series are the invention of the devil". Euler's formula can now be understood rigorously in terms of the Riemann zeta function, and in physics it explains why bosonic strings work best in 26=24+2 dimensions. The fact that

1² + 2² + 3² + … + 24²

is a perfect square then sets up a curious link between string theory, the Leech lattice (the densest known way of packing spheres in 24 dimensions) and a group called the Monster. A better-known but closely related fact is the period-12 phenomenon in the theory of "modular forms". We shall do our best to demystify some of these deep mysteries.

At 7:30 pm on Friday, Anita Chowdry and I gave a joint lecture about the harmonograph as part of a series called the Bridges Lectures, which aim to bridge the gap between mathematics and the arts.

The harmonograph

A harmonograph is a drawing machine powered by pendulums. It was first invented in the 1840s — the heyday of the industrial revolution, whose sensibilities are now celebrated by the "Steampunk" movement.

In this presentation, artist Anita Chowdry will recount her fascinating journey into this era, culminating in her creation of a two-meter high harmonograph crafted from brass and steel: "The Iron Genie". Then, using computer simulations, mathematical physicist John Baez will explore the underlying mathematics of the harmonograph, taking us on a trip into the fourth dimension and beyond. As time passes, the motion of the harmonograph traces out a curve in a multi-dimensional space. The picture it draws is just the two-dimensional "shadow" of this curve.

This presentation will be enhanced by the creative output of a four-day workshop with University of Waterloo students at the department of Fine Arts, led by Anita Chowdry.

The Octonions

The octonions are the largest of the four normed division algebras. While somewhat neglected due to their nonassociativity, they stand at the crossroads of many interesting fields of mathematics. Here we describe them and their relation to Clifford algebras and spinors, Bott periodicity, projective and Lorentzian geometry, Jordan algebras, and the exceptional Lie groups. We also touch upon their applications in quantum logic, special relativity and supersymmetry.

Split Octonions and the Rolling Ball

Understanding exceptional Lie groups as the symmetry groups of more familiar objects is a fascinating challenge. The compact form of the smallest exceptional Lie group, G2, is the symmetry group of an 8-dimensional nonassociative algebra called the octonions. However, another form of this group arises as symmetries of a simple problem in classical mechanics! The space of configurations of a ball rolling on another ball without slipping or twisting defines a manifold where the tangent space of each point is equipped with a 2-dimensional subspace describing the allowed infinitesimal motions. Under certain special conditions, the split real form of G2 acts as symmetries. We can understand this using the quaternions together with an 8-dimensional algebra called the 'split octonions'. The rolling ball picture makes the geometry associated to G2 quite vivid. This is joint work with James Dolan and John Huerta, with animations created by Geoffrey Dixon.

I was invited by Prakash Panandagen to speak at his session Logic, Category Theory and Computation. I gave this talk on Saturday December 5 10-10:30 am:

Categories in Control

Control theory is the branch of engineering that studies dynamical systems with inputs and outputs, and seeks to stabilize these using feedback. Control theory uses 'signal-flow diagrams' to describe processes where real-valued functions of time are added, multiplied by scalars, differentiated and integrated, duplicated and deleted. In fact, these are string diagrams for the symmetric monoidal category of finite-dimensional vector spaces and the monoidal structure is direct sum. Jason Erbele and I found a presentation for this symmetric monoidal category, which amounts to saying that it is the PROP for bicommutative bimonoids with some extra structure.

A broader class of signal-flow diagrams also includes extra morphisms to model feedback. This amounts to working with the symmetric monoidal category where objects are finite-dimensional vector spaces and the morphisms are linear relations. Erbele also found a presentation for this larger symmetric monoidal category. It is the PROP for a remarkable thing: roughly speaking, an object with two commutative Frobenius algebra structures, such that the multiplication and unit of either one and the comultiplication and counit of the other fit together to form a bimonoid.

In electrical engineering we also need a category where a morphism is a circuit made of resistors, inductors and capacitors. Brendan Fong and I proved there is a functor mapping any such circuit to the relation it imposes between currents and potentials at the inputs and outputs. This functor goes from the category of circuits to the category of finite-dimensional vector spaces and linear relations.

The answer to the ultimate question of life, the universe, and everything

In The Hitchhiker's Guide to the Galaxy, by Douglas Adams, the number 42 is revealed to be the "Answer to the Ultimate Question of Life, the Universe, and Everything". But he didn't say what the question was! I will reveal that here. In fact it is a simple geometry question, which turns out to be related to the mathematics underlying string theory.

Network Theory

Nature and the world of human technology are full of networks. People like to draw diagrams of networks: flow charts, electrical circuit diagrams, signal-flow graphs, Bayesian networks, Feynman diagrams and the like. Mathematically minded people know that in principle these diagrams fit into a common framework, namely category theory. But we are still far from a unified theory of networks. Here we explain how networks of various different kinds can be seen morphisms in various different categories, and show how these examples are connected by functors.

Probabilities versus Amplitudes

Some ideas from quantum theory are just beginning to percolate back to classical probability theory. For example, the master equation for a chemical reaction network describes the interactions of molecules in a stochastic rather than quantum way. If we look at it from the perspective of quantum theory, this formalism turns out to involve creation and annihilation operators, coherent states and other well-known ideas — but with a few big differences.

I gave the opening talk at 9 am on Sunday June 28th:

Categories in Control

Control theory is the branch of engineering that studies dynamical systems with inputs and outputs, and seeks to stabilize these using feedback. Control theory uses "signal-flow diagrams" to describe processes where real-valued functions of time are added, multiplied by scalars, differentiated and integrated, duplicated and deleted. In fact, these are string diagrams for the symmetric monoidal category of finite-dimensional vector spaces, but where the monoidal structure is direct sum rather than the usual tensor product. Jason Erbele has given a presentation for this symmetric monoidal category, which amounts to saying that it is the PROP for bicommutative bimonoids with some extra structure.

A broader class of signal-flow diagrams also includes 'caps' and 'cups' to model feedback. This amounts to working with a larger symmetric monoidal category where objects are still finite-dimensional vector spaces but the morphisms are linear relations. Erbele also found a presentation for this larger symmetric monoidal category. It is the PROP for a remarkable thing: roughly speaking, an object with two special commutative dagger-Frobenius structures, such that the multiplication and unit of either one and the comultiplication and counit of the other fit together to form a bimonoid.

Circuits, Categories and Rewrite Rules

We describe a category where a morphism is an electrical circuit made of resistors, inductors and capacitors, with marked input and output terminals. In this category we compose morphisms by attaching the outputs of one circuit to the inputs of another. There is a functor called the 'black box functor' that takes a circuit, forgets its internal structure, and remembers only its external behavior. Two circuits have the same external behavior if and only if they impose same relation between currents and potentials at their terminals. This is a linear relation, so the black box functor goes from the category of circuits to the category of finite-dimensional vector spaces and linear relations. Constructing this functor makes use of Brendan Fong's theory of 'decorated cospans' — and the question of whether two circuits map to the same relation has an interesting answer in terms of rewrite rules.

On Monday a little after 10:30 am, I gave this talk:

Network Theory

Nature and the world of human technology are full of networks. People like to draw diagrams of networks: flow charts, electrical circuit diagrams, signal-flow graphs, Bayesian networks, Feynman diagrams and the like. Mathematically minded people know that in principle these diagrams fit into a common framework. But we are still far from a unified theory of networks. Here we propose compact categories as a general framework - or for a more detailed treatment, compact bicategories. We illustrate this with a number of key examples, and show how these examples are connected by functors.

Networks in Climate Science

The El Niño is a powerful but irregular climate cycle that has huge consequences for agriculture and perhaps global warming. Predicting its arrival more than 6 months ahead of time has been difficult. A recent paper by Ludescher et al caused a stir by using ideas from network theory to predict the start of an El Niño toward the end of 2014 with a 3-in-4 likelihood. After explaining the basics of El Niño and climate network theory, we critically analyze their method and address the question: are El Niños signaled by an increase in temperature correlations between regions of the Pacific within the El Niño basin and those outside it?

• Thursday April 16 - I took a 6:15 am flight from State College to LAX.

• Wednesday April 15 - at 12:05 - 1:20 pm I spoke at the Geometry Luncheon Seminar on my work with Greg Egan on the Leech lattice and the exceptional Jordan algebra:

  The Exceptional Jordan Algebra and the Leech Lattice

  When Jordan, Wigner and von Neumann classified algebras of observables in their work on the foundations of quantum mechanics, they found 4 infinite series and one exception. This 'exceptional Jordan algebra' is 27-dimensional and consists of 3×3 self-adjoint octonionic matrices. The Leech lattice is another exceptional structure: the unique 24-dimensional even unimodular lattice with no vectors of length squared 2. I'll explain these entities and describe some work with Greg Egan where we made the Leech lattice into a 'Jordan subring' of the exceptional Jordan algebra.

  At 2:30 pm my time I gave a virtual public lecture at the University of York. This was 7:30 pm in the UK. The talk actually started half an hour later. My host is Stijn Hanson. I talked for about an hour and then answered some questions.

  8

  Different numbers have different personalities, and 8 is one of my favorites. The number 8 plays a special role in mathematics due to the "octonions", an 8-dimensional number system where one can add, multiply, subtract and divide, but multiplication is noncommutative and nonassociative. The octonions were discovered by Hamilton's friend John Graves in 1843 after Hamilton told him about the "quaternions". While much neglected, they stand at the crossroads of many interesting branches of mathematics and physics. For example, superstring theory works in 10 dimensions because 10 = 8+2, where 8 is the dimension of the octonions. Also, the densest known packing of spheres in 8 dimensions occurs when the spheres are centered at certain "integer octonions", which form the root lattice of the exceptional Lie group E8. The octonions also explain the curious way in which topology in dimension n resembles topology in dimension n+8.

  After this talk I spoke with Aissa Wade at 317 McAllister.

• Tuesday April 14 - at 9 am I worked with Stijn Hanson to get the computer set up for my virtual talk at the University of York on Wednesday.

  Around 10:30 am I met Jason Morton at 219B McAllister.

  At 12 I met Abhay Ashtekar at 316 Whitmore Laboratory and have lunch with him, Marc Geiller and Eugenio Bianchi

  At 2:30 - 3:20 pm I gave this talk in the Geometry-Analysis-Physics Seminar at 106 McAllister:

  Split octonions and the rolling ball

  Understanding exceptional Lie groups as the symmetry groups of more familiar objects is a fascinating challenge. The compact form of the smallest exceptional Lie group, G₂, is the symmetry group of an 8-dimensional nonassociative algebra called the octonions. However, another form of this group arises as symmetries of a simple problem in classical mechanics! The space of configurations of a ball rolling on another ball without slipping or twisting defines a manifold where the tangent space of each point is equipped with a 2-dimensional subspace describing the allowed infinitesimal motions. Under certain special conditions, the split real form of G₂ acts as symmetries. We can understand this using the quaternions together with an 8-dimensional algebra called the 'split octonions'. The rolling ball picture makes the geometry associated to G₂ quite vivid. This is joint work with James Dolan and John Huerta, with animations created by Geoffrey Dixon.

  At 6 pm there was a party at John Roe's house.

• Monday April 13 - At 11:20 am - 12:20 pm I had lunch with Jason Morton and Sara Jamshidi at the Allen Street Grill.

  At 2:30 pm I gave a talk on Climate Networks in John Roe's class at 2:30 pm in 115 Osmond. It's a 50-minute class:

  Math 033 - Mathematics for Sustainability

  The course meets Mondays, Wednesdays and Fridays at 2:30 in 115 Osmond. Class sessions last for 50 minutes and are divided roughly 60:40 between 'theory' classes — where the central theme is a mathematical idea — and 'case studies' — where the central theme is a particular example of sustainability practice and how it can be analyzed mathematically.

  The aim of the class is to reach students who do not have an extensive mathematical background. High school algebra is the only prerequisite for the class. As the semester progresses we will introduce some more ideas related to 'measuring' (unit systems, scientific notation, specific discussion of energy); 'changing' (stocks, flows, equilibrium, dynamics, tipping points); 'risking' (probability, inference, decision-making under uncertainty); and 'networking' (networks, connectivity, strong and weak ties). Please bear this level of background knowledge in mind as you prepare your presentation. The students will be eager to hear how the ideas that they have been learning relate to the real-world experience that you can bring to the table.

Here is my talk:

Information and entropy in biological systems

Information and entropy are being used in biology in many different ways: for example, to study biological communication systems, the 'action-perception loop', the thermodynamic foundations of biology, the structure of ecosystems, measures of biodiversity, and evolution. Can we unify these? To do this, we must learn to talk to each other. This will be easier if we share some basic concepts which I'll sketch here.

• The Cameron Trading Post
• The Sacred Canyon Lodge, in Canyon de Chelly
• The Holiday Inn in Cortez, Arizona (2 nights)
• The El Rancho Hotel in Gallup, New Mexico
• The Quality Inn in Winslow, Arizona
• One of the two Best Western hotels in Kingman, Arizona

I went to the NIPS Speaker's dinner at the Hyatt Regency Hotel Hotel on Tuesday, December 9th, 2014.

I gave this talk at 9 am on Wednesday December 10th:

Networks in climate science

The El Niño is a powerful but irregular climate cycle that has huge consequences for agriculture and perhaps global warming. Predicting its arrival more than 6 months ahead of time has been difficult. A recent paper by Ludescher et al caused a stir by using ideas from network theory to predict the start of an El Niño toward the end of 2014 with a 3-in-4 likelihood. After explaining the basics of El Niño and climate network theory, we critically analyze their method and address the question: are El Niños signaled by an increase in temperature correlations between regions of the Pacific within the El Niño basin and those outside it?

Biodiversity, entropy and thermodynamics

The most popular measures of biodiversity are formally identical to the measures of entropy developed by Shannon, Rényi and others. This fits into a larger analogy between thermodynamics and the mathematics of biodiversity. For example, in certain models of evolutionary game theory one can show that as population approaches an 'evolutionary optimum', the amount of information it has 'left to learn' is nonincreasing. This is mathematically analogous to the Second Law of Thermodynamics.

• The computational power of chemical reaction networks.
• Chemical reaction network talks.

• Sunday June 1, 2014 - Flight from Nuremberg back to LAX, leaving at 10:20 am and arriving at 7:15 pm.

• Monday May 26, 2014 - At 4:15 I spoke at the computer science department at Room 01.150-128, Cauerstrasse 11, 91058 Erlangen. Cauerstrasse 11 is the new mathematics / CS building, which is building 128 on this map. My host, Lutz Schöder, wrote.

  If you arrive before 4pm, then we could just meet at the theory chair, which is rather easier to find: we're in the so-called blue highrise, Martensstr. 3, which you cannot miss once you're at Technische Fakultät (it is, well, a blue highrise...), on floor 11 (the floors are small, so you'll find us). I myself will have to teach until 3:45 pm, but most of the other guys (some of them in the CC), including, I believe, our secretary Mrs. Schünberger (CC), will be there all afternoon, so you're welcome to drop by for coffee.

  Here is my talk:

  Network Theory

  We are entering the Anthropocene, a new geological epoch in which the biosphere is strongly affected by human activities. So, we can expect the science of this century to draw inspiration from biology, ecology and the environmental problems that confront us. What can category theorists, of all people, have to say about this? Researchers in many fields draw diagrams of networks: flow charts, Petri nets, Bayesian networks, electrical circuit diagrams, signal-flow graphs, Feynman diagrams and the like. In principle these diagrams fit into a common framework: category theory. But we are still far from a unified theory of networks. We give an overview of the theory as it stands now, with an emphasis on topics for future research, some involving higher categories.

• May 10 - 24, 2014 - I attended the Institut Henri Poincaré thematic trimester Semantics of proofs and certified mathematics. Lisa attended a conference on May 20.

  • Wednesday May 21, 2014 - from 4 to 6 pm I spoke at Anatole Khelif's seminar Catégories, Logiques, Etc... in the 1er étage of Batiment Sophie Germain, in room 1006. This building is on the crossing of Avenue de France rue Alice-Domon et Leonie-Duquet, 5 minutes from the metro station "Bibliotheque F. Mitterrand". I spoke about the categorified Heisenberg algebra:

    Spans and the Categorified Heisenberg Algebra

    Heisenberg reinvented matrices while discovering quantum mechanics, and the algebra generated by annihilation and creation operators obeying the canonical commutation relations was named after him. It turns out that matrices arise naturally from 'spans', where a span between two objects is just a third object with maps to both those two. In terms of spans, the canonical commutation relations have a simple combinatorial interpretation.

    More recently, Khovanov introduced a 'categorified' Heisenberg algebra, where the canonical commutation relations hold only up to isomorphism, and these isomorphisms obey new relations of their own. The categorified Heisenberg algebra naturally acts on the '2-Fock space' describing collections of particles in a 4-dimensional topological quantum field theory.

    The meaning of the new relations in the categorified Heisenberg algebra was initially rather mysterious. However, Jeffrey Morton and Jamie Vicary have shown that they again have a nice interpretation in terms of spans. We can begin to formalize this using the work of Alex Hoffnung and Mike Stay, who have shown that spans of groupoids are morphisms in a symmetric monoidal bicategory.

  • Tuesday May 20, 2014 - from 9:30 to 10:30 am I gave a talk at the Institut Henri Poincaré as part of a 3-day session on operads, Journées de la Fédération de recherche en mathématiques de Paris-Centre:

    Operads and the Tree of Life

    Trees are not just combinatorial structures: they are also biological structures, both in the obvious way but also in the study of evolution. Starting from DNA samples from living species, biologists seek to reconstruct the most likely phylogenetic tree describing how these species evolved from earlier ones. In fact, phylogenetic trees are operations in an operad, the "phylogenetic operad", which plays a universal role in the study of branching Markov processes. To understand this operad, and more generally the relation between operads and trees, we use the fact that operads are themselves the algebras of a (typed) operad. This is joint work with Nina Otter and Todd Trimble.

  • Friday May 16, 2014 - I spoke in the topology seminar in Lille at 2 pm. My host is Benoit Fresse. Lille is just 1 hour from the Paris-Nord train station by TGV, and there is approximately one departure every hour. The university can also easily be reached in Lille; there is an automatic subway line that takes you in 15 minutes from the main train station to the center of the campus. I took the train leaving Paris-Nord at 10:46 and arriving in Lille at 11:48.

    Operads and the Tree of Life

    Trees are not just combinatorial structures: they are also biological structures, both in the obvious way but also in the study of evolution. Starting from DNA samples from living species, biologists seek to reconstruct the most likely phylogenetic tree describing how these species evolved from earlier ones. In fact, phylogenetic trees are operations in an operad, the "phylogenetic operad", which plays a universal role in the study of branching Markov processes. To understand this operad, and more generally the relation between operads and trees, we use the fact that operads are themselves the algebras of a (typed) operad. This is joint work with Nina Otter and Todd Trimble.

• April 28 - 29 - Lisa gave a talk in Leipzig.

• April 27 - May 2, 2014 - I helped run a Dagstuhl Perspectives Workshop on Categorical Methods at the Crossroads. This was held in a German castle called Schloss Dagstuhl which has become a center for computer science. The idea is to get people who apply category theory to lots of different subjects to talk to each other. I ran this with Samson Abramsky and Fabio Gadducci (in computer science) and Viktor Winschel (in economics).

  On May 2, I gave this talk:

  Network Theory

  We are entering the Anthropocene, a new geological epoch in which the biosphere is strongly affected by human activities. Thus, just as 20th-century mathematics drew inspiration from physics, we can expect 21st-century mathematics to draw inspiration from biology, ecology and the environmental problems that confront us. What do category theorists, of all people, have to say about this? Researchers in many fields draw diagrams of networks: flow charts, electrical circuit diagrams, signal-flow graphs, Bayesian networks, Feynman diagrams and the like. In principle these diagrams fit into a common framework: category theory. But we are still far from a unified theory of networks. We give an overview of the theory as it stands now, with an emphasis on topics for future research, some involving higher categories.

  • Arrival date: Sunday, April 27 (afternoon)
  • Departure date: Friday, May 2, 2014 (afternoon)

  Arrival and departure information:

  Kindly check in with our reception staff when you arrive at Schloss Dagstuhl. Our reception office, located in the newer facility just left of the main building, is open from 3 p.m. to 7 p.m. on Sundays and holidays and from 8 a.m. to 4 p.m. on other days. If reception is closed when you arrive, please [....] A buffet dinner is available at the Schloss on Sundays from 6 p.m. until the following morning.

• April 10 - 17 - I attended the Institut Henri Poincaré thematic trimester Semantics of proofs and certified mathematics and spent a lot of time talking to Paul-André Melliès. Lisa attended a conference on April 11.

• Tuesday April 1 - Thursday April 3 - Lisa and I visited Bern, where she gave a talk at the Institute for Philosophy.

• Friday February 21 - Friday March 14, 2014 - I visited England, especially Oxford, but also Cambridge and Birmingham.
  • Wednesday March 12 - I took a train from Oxford up to Cambridge. I gave a talk at the Department of Pure Mathematics and Mathematical Statistics on 5-6 pm on Wednesday in Meeting Room 2:

    The Mathematics of Planet Earth

    The global warming crisis is part of a bigger transformation in which humanity realizes that the Earth is a finite system and that our population, energy usage, and the like cannot continue to grow exponentially. If civilization survives this transformation, it will affect mathematics — and be affected by it — just as dramatically as the agricultural revolution and industrial revolution did. We cannot know for sure what the effect will be, but we can already make some guesses.

    On Wednesday after my talk a bunch of people including students of Martin Hyland and Peter Johnstone had drinks at a pub, and then I went to dinner at Trinity with Bela Bollobas. On Thursday I had lunch at Trinity with Tim Gowers and Huw Price. On Thursday evening Lisa and I had dinner at the Gowers' house. On Friday we returned to Erlangen.

  • Tuesday March 11, 2014 - At 11:15 I met Brendan Fong and Heather Harrington in the café at the Mathematical Institute in Oxford.

  • Friday March 7, 2014 - From 2-4 I spoke about applications of category theory with Jocelyn Ireson-Paine and Ian Bentley in the lounge at the computer science department in Oxford.

  • Thursday March 6, 2014 - At 12:30 pm I spoke to Leron Borsten about octonions, meeting him at Brown's, near the computer science department in Oxford. At 4 pm I spoke to Jamie Vicary and Chris Douglas about conformal field theory, in the Mathematical Institute.

  • Tuesday March 4, 2014 - I gave a talk on Fock space techniques for stochastic physics in the Quantum Field Theory seminar run by Keith Hannabuss, at 12 noon in Lecture Room 5 in the Maths Institute at Oxford.

  • Wednesday February 26, 2014 - I took a train from Oxford to the computer science department in Birmingham, where I'd been invited by Dan Ghica to gave a talk at 4-5 pm in Haworth 101:

    The Mathematics of Planet Earth

    The global warming crisis is part of a bigger transformation in which humanity realizes that the Earth is a finite system and that our population, energy usage, and the like cannot continue to grow exponentially. If civilization survives this transformation, it will affect mathematics — and be affected by it — just as dramatically as the agricultural revolution and industrial revolution did. We cannot know for sure what the effect will be, but we can already make some guesses.

  • Monday February 24, 2014 - I was invited by Ulrike Tillmann to give a talk in the topology seminar at 3:30 pm in Oxford:

    Operads and the Tree of Life

    Trees are not just combinatorial structures: they are also biological structures, both in the obvious way but also in the study of evolution. Starting from DNA samples from living species, biologists use increasingly sophisticated mathematical techniques to reconstruct the most likely 'phylogenetic tree' describing how these species evolved from earlier ones. In their work on this subject, they have encountered an interesting example of an operad, which is obtained by applying a variant of the Boardmann–Vogt 'W construction' to the operad for commutative monoids. The operations in this operad are labelled trees of a certain sort, and it plays a universal role in the study of stochastic processes that involve branching. It also shows up in tropical algebra. This talk is based on work in progress with Nina Otter.

    This took place in the Mathematical Institute building.

  • Friday February 21 - Friday March 14, 2014 - I visited Bob Coecke's group at the computer science department in Oxford and gave a series of four talks on network theory:

    Network Theory

    Nature and the world of human technology are full of networks. People like to draw diagrams of networks: flow charts, electrical circuit diagrams, signal-flow graphs, Bayesian networks, Feynman diagrams and the like. Mathematically minded people know that in principle these diagrams fit into a common framework: category theory. But we are still far from a unified theory of networks. After an overview, we will look at three portions of the jigsaw puzzle in three separate talks.

    All these talks took place in Lecture Theatre B in the Computer Science Department:

    • Friday 21 February 2014, 2 pm: Network Theory: overview.
    • Tuesday 25 February, 3:30 pm: Network Theory I: electrical circuits and signal-flow graphs.
    • Tuesday 4 March, 3:30 pm: Network theory II: stochastic Petri nets, chemical reaction networks and Feynman diagrams.
    • Tuesday 11 March, 3:30 pm: Network Theory III: Bayesian networks, information and entropy.

    The first talk was part of the OASIS series, meaning the "Oxford Advanced Seminar on Informatic Structures".

    Also: Minhyong Kim organized an informal seminar on quantum gravity meeting 10:30-12+ε on the Fridays February 28 and March 7, meeting at Merton College, followed by lunch.

• Wednesday February 5 - I gave a talk at the Mathematical Physics Seminar at the Friedrich-Alexander-Universität Erlangen-Nürnberg:

  Categories in Control

  Control theory is the branch of classical mechanics that deals with 'open systems': physical systems like machines, where the time evolution depends on parameters that can be changed in a time-dependent way by an external agent. We can take small open systems and glue them together to form larger ones. This means that category theory is relevant: we can treat open systems as 'morphisms', and glue them together by composing or tensoring them. Here we describe some small steps toward a category-theoretic approach to control theory.

Life's Struggle to Survive

When pondering the number of extraterrestrial civilizations, it is worth noting that even after it got started, the success of life on Earth was not a foregone conclusion. We recount some thrilling episodes from the history of our planet, some well-documented but others merely theorized: our collision with the planet Theia, the oxygen catastrophe, the snowball Earth events, the Permian-Triassic mass extinction event, the asteroid that hit Chicxulub, and more, including the global warming episode we are causing now. All of these hold lessons for what may happen on other planets.

The Mathematics of Planet Earth

The International Mathematical Union has declared 2013 to be the year of The Mathematics of Planet Earth. The global warming crisis is part of a bigger transformation in which humanity realizes that the Earth is a finite system and that our population, energy usage, and the like cannot continue to grow exponentially. If civilization survives this transformation, it will affect mathematics — and be affected by it — just as dramatically as the agricultural revolution or industrial revolution. We cannot know for sure what the effect will be, but we can already make some guesses.

Petri Nets, Chemistry, and Quantum Theory

Chemists use "chemical reaction networks" to describe random interactions between things of different types. These are essentially the same as what computer scientists call "Petri nets", or mathematicians would call "free symmetric monoidal categories". The reachability problem for a Petri net asks which collections of things can turn into which other collections of things: it is decidable but hard. More relevant to chemistry is the master equation, a differential equation describing how the probability that some collection will turn into some other collection changes with time. This turns out to have a nice description using some math from quantum field theory, but with probabilities replacing amplitudes.

The invited scholars, each from a different disciplines, were asked to make two fairly short presentations on the basis of prepared position papers. On the first day each presenter will address the question "what is climate change?" On the second day each presenter addressed the question "what should we do about it?"

Each day consisted of three sessions for presentations followed by a lengthy roundtable where the commonalities and differences between the various disciplines can be teased out, with the aid of some BSIA and MCC graduate student facilitators. Presentations, and the papers they are based on, were not circulated prior to the workshop so that there is a certain surprise element during the event to focus attention on the details of both definition and response.

My talks are here: What is Climate Change? and What To Do About Climate Change?

Learning to Live on a Finite Planet

The global warming crisis is part of a bigger transformation in which humanity realizes that the Earth is a finite system and that our population, energy usage, and the like cannot continue to grow exponentially. The transformation is inevitable. The big question is, what can we do to make it more pleasant?

Spans and the Categorified Heisenberg Algebra

Heisenberg reinvented matrices while discovering quantum mechanics, and the algebra generated by annihilation and creation operators obeying the canonical commutation relations was named after him. It turns out that matrices arise naturally from 'spans', where a span between two objects is just a third object with maps to both those two. In terms of spans, the canonical commutation relations have a simple combinatorial interpretation. More recently, Khovanov introduced a 'categorified' Heisenberg algebra, where the canonical commutation relations hold only up to isomorphism, and these isomorphisms obey new relations of their own. The meaning of these new relations was initially rather mysterious. However, Jeffrey Morton and Jamie Vicary have shown that these, too, have a nice interpretation in terms of spans. Moreover, the categorified Heisenberg algebra naturally acts on the '2-Fock space' describing collections of particles in a 4-dimensional topological quantum field theory.

Learning to Live on a Finite Planet

The global warming crisis is part of a bigger transformation in which humanity realizes that the Earth is a finite system and that our population, energy usage, and the like cannot continue to grow exponentially. The transformation is inevitable. The big question is, what can we do to make it more pleasant?

Spans and the Categorified Heisenberg Algebra

Heisenberg reinvented matrices while discovering quantum mechanics, and the algebra generated by annihilation and creation operators obeying the canonical commutation relations was named after him. It turns out that matrices arise naturally from 'spans', where a span between two objects is just a third object with maps to both those two. In terms of spans, the canonical commutation relations have a simple combinatorial interpretation. More recently, Khovanov introduced a 'categorified' Heisenberg algebra, where the canonical commutation relations hold only up to isomorphism, and these isomorphisms obey new relations of their own. The meaning of these new relations was initially rather mysterious. However, Jeffrey Morton and Jamie Vicary have shown that these, too, have a nice interpretation in terms of spans. We can begin to formalize this using the work of Alex Hoffnung and Mike Stay, who have shown that spans of groupoids are morphisms in a symmetric monoidal bicategory.

• August 6: Lisa and I fly from Singapore to Dunhuang, the far-west Chinese town famous for its caves, the Mogao caves. The flight is absurdly long, leaving at 3 am, changing planes twice, and arriving at 9:30 pm that day.
• We visited the Western Thousand Buddha Caves.
• We visted the Mogao Caves and saw some caves not on the usual tour.
• August 8: Our mathematician friend Weiwei Pan showed up and we visited the night market.
• August 9: We rode camels in the Mingshan Sand Dunes and visited Crescent Lake in the morning. In the afternoon we took a camel trek into the desert and camped out there overnight.
• August 10: We returned to Dunhuang in the morning and went to see rock formations in Yandan (on the way: Han Great Wall, Yumen Pass).
• August 11: We visited the Mogao Caves again and took the public tour.
• August 12: Lisa and I flew to Lanzhou at 7 pm.
• August 13: Lisa left for Singapore in the afternoon.
• August 14-16: math conference in Langzhou.
• August 17: A bunch of conference participants including Chengchang and Weiwei and I took a tour bus south to Labrang Monastery - a Tibetan monastery.
• August 18: we went to Langmusi, a town at the border of Ganus Province and Sichuan Province.
• August 19: we returned to Lanzhou.
• August 20: I flew back to Singapore

Key Developments in Category Theory

From the invention of categories in 1945 to the rise of homotopy type theory in recent years, category theory has been exceptionally rich in philosophically interesting ideas. I will try to outline some of the key developments with a minimum of technical detail.

Then I went to their Category-Theoretic Foundations of Mathematics Workshop that weekend, where I gave the following talk at Sunday May 5th at 9 am:

The Foundations of Applied Mathematics

Suppose we take "applied mathematics" in an extremely broad sense that includes math developed for use in electrical engineering, population biology, epidemiology, chemistry, and many other fields. Suppose we look for mathematical structures that repeatedly appear in these diverse contexts — especially structures that aren't familiar to pure mathematicians. What do we find? The answers may give us some clues about the concepts that underlie the most applicable kinds of mathematics. We should not be surprised to find some category theory here.

5

Different numbers have different personalities. The number 5 is quirky and intriguing, thanks in large part to its relation with the golden ratio, the "most irrational" of irrational numbers. It is impossible to tile the plane with regular pentagons, or form a crystal with perfect 5-fold symmetry... but trying leads to some beautiful things.

Milankovitch Cycles and the Earth's Climate

In the last few million years the Earth's climate has been dominated by dramatic swings in temperature between cold 'glacials' and warm 'interglacials'. The most widely accepted theory says that these are triggered by Milankovitch cycles: periodic changes in the Earth's orbital parameters. However, the details are far from fully understood, leaving many puzzles for us to study.

Energy and the Environment - What Physicists Can Do

The global warming crisis is part of a bigger transformation in which humanity realizes that the Earth is a finite system and that our population, energy usage, and the like cannot continue to grow exponentially. While politics and economics pose the biggest challenges, physicists are in a good position to help make this transition a bit easier. After a quick review of the problems, we discuss a few ways physicists can help.

I left on Saturday, I arrived at Heathrow at about 2:50 on Sunday the 24th, and then I took a train to Sheffield, arriving at a pub called Brown's at about 9:00 pm, where a bunch of people had gathered, including Eugenia Cheng, Tom Leinster, Simon Willerton and Nick Gurski.

On Monday the 25th from 2 to 2:25 pm I gave a talk on "Bicategories and Tricategories of Spans" at a satellite meeting of the British Mathematics Colloquium, 94th Peripatetic Seminar on Sheaves and Logic.

Later that day, from 18:30 to 19:30, I gave this public lecture:

The Mathematics of Planet Earth

The International Mathematical Union has declared 2013 to be the year of The Mathematics of Planet Earth. The global warming crisis is part of a bigger transformation in which humanity realizes that the Earth is a finite system and that our population, energy usage, and the like cannot continue to grow exponentially. If civilization survives this transformation, it will affect mathematics — and be affected by it — just as dramatically as the agricultural revolution or industrial revolution. We cannot know for sure what the effect will be, but we can already make some guesses.

After this a bunch of us went to an Indian restaurant called Aagrah, where Eugenia Cheng booked a large table.

On Wednesday the 27th, I spoke on a panel on open access from 11:30 to 12:45. Later that day I went to Nottingham to give a talk at 17:00:

Spans and the Categorified Heisenberg Algebra

Heisenberg reinvented matrices while discovering quantum mechanics, and the algebra generated by annihilation and creation operators obeying the canonical commutation relations was named after him. It turns out that matrices arise naturally from 'spans', where a span between two objects is just a third object with maps to both those two. In terms of spans, the canonical commutation relations have a simple combinatorial interpretation. More recently, Khovanov introduced a 'categorified' Heisenberg algebra, where the canonical commutation relations hold only up to isomorphism, and these isomorphisms obey new relations of their own. The meaning of these new relations was initially rather mysterious. However, Jeffery Morton and Jamie Vicary have shown that these, too, have a nice interpretation in terms of spans.

On Thursday the 28th the conference ended at 12:30, and I met David Tweed and later also Jim Stuttard and Glyn Adgie.

The Mathematics of Planet Earth

The International Mathematical Union has declared 2013 to be the year of The Mathematics of Planet Earth. The global warming crisis is part of a bigger transformation in which humanity realizes that the Earth is a finite system and that our population, energy usage, and the like cannot continue to grow exponentially. If civilization survives this transformation, it will affect mathematics — and be affected by it — just as dramatically as the agricultural revolution or industrial revolution. We cannot know for sure what the effect will be, but we can already make some guesses.

The Mathematics of Planet Earth

The International Mathematical Union has declared 2013 to be the year of The Mathematics of Planet Earth. The global warming crisis is part of a bigger transformation in which humanity realizes that the Earth is a finite system and that our population, energy usage, and the like cannot continue to grow exponentially. If civilization survives this transformation, it will affect mathematics — and be affected by it — just as dramatically as the agricultural revolution or industrial revolution. We cannot know for sure what the effect will be, but we can already make some guesses.

On July 5, I gave this talk:

Diversity, Entropy and Thermodynamics

As is well known, some popular measures of biodiversity are formally identical to measures of entropy developed by Shannon, Rényi and others. This fact is part of a larger analogy between thermodynamics and the mathematics of biodiversity, which we explore here. Any probability distribution can be extended to a 1-parameter family of probability distributions where the parameter has the physical meaning of 'temperature'. This allows us to introduce thermodynamic concepts such as energy, entropy, free energy and the partition function in any situation where a probability distribution is present . for example, the probability distribution describing the relative abundances of different species in an ecosystem. The Rényi entropy of this probability distribution is closely related to the change in free energy with temperature. We give one application of thermodynamic ideas to population dynamics, coming from the work of Marc Harper: as a population approaches an 'evolutionary optimum', the amount of Shannon information it has 'left to learn' is nonincreasing. This fact is closely related to the Second Law of Thermodynamics.

On June 14 I gave a talk at the Preuves, Programmes et Systèmes group at Université Paris 7:

Stochastic Petri Nets and Chemical Reactions

Chemists use "chemical reaction networks" to describe random interactions between things of different types. These are essentially the same as what computer scientists call "stochastic Petri nets". From such a structure, we can obtain a differential equation describing time evolution. A simple criterion implies that this equation has stationary solutions. This criterion involves a generalization of Euler characteristic to stochastic Petri nets.

G₂ and the Rolling Ball

Understanding the exceptional Lie groups as the symmetry groups of simpler objects is a longstanding challenge. Here we describe how the smallest exceptional Lie group, G₂, shows up as symmetries of a simple physics problem: a ball rolling on a larger ball without slipping or twisting. G2 acts as symmetries of this problem, but only when we treat the smaller ball as a 'spinor', which returns to its orientation not after one full turn but only after two — and only when the larger ball is 3 times as big as the smaller one. We show how to understand this special ratio, describe the geometry of the rolling ball system in terms of imaginary split octonions, and show how geometric quantization applied to this system lets us recover the imaginary split octonions together with their cross product.

Teleparallel Gravity as a Higher Gauge Theory

Higher gauge theory uses '2-connections' to describe parallel transport not only along curves, but also over surfaces. Just as gauge theory uses Lie groups, higher gauge theory uses Lie 2-groups. We show that general relativity can be viewed as a higher gauge theory. On any semi-Riemannian manifold M, we construct a principal 2-bundle with the the 'teleparallel 2-group' as its structure 2-group. Any flat metric-preserving connection on M gives a flat 2-connection on this 2-bundle, and the key ingredient of this 2-connection is the torsion. Taking advantage of Einstein and Cartan's formulation of general relativity in which a flat connection and its torsion are are key ingredients, this lets us rewrite general relativity as a theory with a 2-connection for the teleparallel 2-group as its only field.

Energy, the Environment and What We Can Do

Our heavy reliance on fossil fuels is causing two serious problems: global warming, and the decline of cheaply available oil reserves. Unfortunately the second problem will not cancel out the first. Each one individually seems extremely hard to solve, and taken together they demand a major worldwide effort starting now. After an overview of these problems, we turn to the question: what can we do about them?

I gave the Mathematics Colloquium at 1 pm Monday 6 February 2012, in E7B T2:

Probabilities versus Amplitudes

Some ideas from quantum theory are just beginning to percolate back to classical probability theory. For example, there is a widely used and successful theory of "chemical reaction networks", which describes the interactions of molecules in a stochastic rather than quantum way. If we look at it from the perspective of quantum theory, this turns out to involve creation and annihilation operators, coherent states and other well-known ideas - but with a few big differences. The stochastic analogue of quantum field theory is also used in population biology, and here the connection is well-known. But what does it mean to treat wolves as identical bosons?

Tuesday the 7th at 1 pm in E7B T2 I gave this talk:

Energy, the Environment and What We Can Do

Our heavy reliance on fossil fuels is causing two serious problems: global warming, and the decline of cheaply available oil reserves. Unfortunately the second problem will not cancel out the first. Each one individually seems extremely hard to solve, and taken together they demand a major worldwide effort starting now. After an overview of these problems, we turn to the question: what can we do about them?

Wednesday the 8th at 2 pm in E7A 333, after lunch with the category theorists, I gave this talk in the Australian Category Seminar:

Symmetric Monoidal Categories in Chemistry and Biology

Chemists use "chemical reaction networks" to describe interactions between things of different types. In population biology and the study of infectious diseases, "stochastic Petri nets" are sometimes used for the same purpose. In fact chemical reaction networks and stochastic Petri nets are essentially the same thing. The theory of symmetric monoidal categories can help us understand what this thing is, and how to work with it.

Talks started at 10 am on Monday the 30th, finishing 5 pm on Thursday the 2nd. There was be a workshop banquet on Tuesday 31 January, and a free afternoon on Wednesday 1 February. My contact people were Gavin Brennen and Stephen Bartlett. My talk lasted 45 minutes, starting 9 am on Wednesday:

Probabilities versus Amplitudes

Some ideas from quantum theory are just beginning to percolate back to classical probability theory. For example, there is a widely used and successful theory of "chemical reaction networks", which describes the interactions of molecules in a stochastic rather than quantum way. If we look at it from the perspective of quantum theory, this turns out to involve creation and annihilation operators, coherent states and other well-known ideas - but with a few big differences. The stochastic analogue of quantum field theory is also used in population biology, and here the connection is well-known. But what does it mean to treat wolves as identical bosons?

The theme for EQuaLS5 was "Geometry, Topology and Physics 2012" and the speakers were:

1. John Baez (NUS, Univ of California, Riverside) "Network Theory"
2. Do Ngoc Diep (Inst of Math, Hanoi) "A Procedure for Quantization of Fields"
3. Varghese Mathai (University of Adelaide) "Noncommutative Geometry and the Fractional Quantum Hall Effect"
4. Fredrik Stroemberg (Technical Univ. of Darmstadt) "Arithmetic Quantum Chaos"
5. S. Twareque Ali (Concordia University, Montreal) "Coherent States: Theory and Applications"

My talks on "Network Theory" were at 10:00 on Monday the 9th, 15:00 on Tuesday, 9:00 on Thursday and 9:00 on Friday. My public talk was at 15:00 on Friday, with the following topic:

Energy, the Environment and What We Can Do

Our heavy reliance on fossil fuels is causing two serious problems: global warming, and the decline of cheaply available oil reserves. Unfortunately the second problem will not cancel out the first. Each one individually seems extremely hard to solve, and taken together they demand a major worldwide effort starting now. After an overview of these problems, we turn to the question: what can we do about them?

Probabilities versus Amplitudes

Some ideas from quantum theory are just beginning to percolate back to classical probability theory. For example, there is a widely used and successful theory of "chemical reaction networks", which describes the interactions of molecules in a stochastic rather than quantum way. If we look at it from the perspective of quantum theory, this turns out to involve creation and annihilation operators, coherent states and other well-known ideas - but with a few big differences. The stochastic analogue of quantum field theory is also used in population biology, and here the connection is well-known. But what does it mean to treat wolves as fermions or bosons?

Lisa and I flew from Singapore to Beijing on Air China flight CA976, leaving at 9:30 on July 29 and arriving at 15:30 at Terminal 3.

We took a train to Changchun on August 2. The train ride took 6 hours and 20 minutes.

From the 3rd to 6th we went on an excursion to Baekdu Mountain, tallest of the Changbai Mountains.

On Sunday the 7th we returned to Changchun and Lisa flew back to Beijing and thence to Singapore.

August 8th-10th I gave three one-hour talks on Higher gauge theory, division algebras and superstrings.

Then I took a train or plane back to Beijing. I left Beijing from Terminal 3 on Air China flight CA969, at 15:35 on August 12.

Yunhe Sheng of the department of mathematics at Jilin University wrote:

Probably, you will arrive at Beijing first and spend several days there. We can also arrange your lodging in Beijing. If so, you are also invited to give a talk at Capital Normal University in Beijing. It is very convenient to take a train to go to Changchun from Beijing, which will take about 6 hours and 20 minutes. I will arrange students to buy train tickets for you and pick you up at Changchun Railway station.

Here's a more detailed description of the trip to the Changbai Mountains:

... we can travel 4 days, 3-6 August. On August 3rd we start after breakfast; hopefully we will arrive at Lanjing (a hotel inside the park, Landscape of English) around 3-4 pm and we can have a walk up Changbai Mountain, maybe. On August 4th we will go to see Tianchi, Pubu, Dixiasenlin, and etc. (points to see in the park). We will go to another hotel for Wenquan (hot spring) that night. On August 5th we will go to Senjiaolongwan. We do not need to start very early that day since we have enough time. We will stay around Sanjiaolongwan. Then on the morning August 6th we will come back, and arrive at Changchun before dinner time.

Operads and the Tree of Life

Trees are not just combinatorial structures: they are also biological structures, both in the obvious way but also in the study of evolution. Starting from DNA samples from living species, biologists use increasingly sophisticated mathematical techniques to reconstruct the most likely "phylogenetic tree" describing how these species evolved from earlier ones. In their work on this subject, they have encountered an interesting example of an operad, which is obtained by applying a variant of the Boardmann-Vogt "W construction" to the operad for commutative monoids. The operations in this operad are labelled trees of a certain sort, and it plays a universal role in the study of stochastic processes that involve branching. We shall explain these ideas assuming a bare minimum of prerequisites.

I gave this talk on the 17th:

Higher gauge theory, division algebras and superstrings

Classically, superstrings make sense when spacetime has dimension 3, 4, 6, or 10. It is no coincidence that these numbers are two more than 1, 2, 4, and 8, which are the dimensions of the normed division algebras: the real numbers, complex numbers, quaternions and octonions. We sketch an explanation of this already known fact and its relation to "higher gauge theory". Just as gauge theory describes the parallel transport of supersymmetric particles using Lie supergroups, higher gauge theory describes the parallel transport of superstrings using "Lie 2-supergroups". Recently John Huerta has shown that we can use normed division algebras to construct a Lie 2-supergroup extending the Poincaré supergroup when spacetime has dimension 3, 4, 6 and 10.

• John Huerta: Wednesday 5/18 from 1 pm to 2:30 pm.
• Chris Rogers: Thursday 5/19 from 3:40 pm to 6:40 pm.
• Christopher Walker: Friday 5/20 from 2:30 pm to 4:00 pm.

On Sunday May 22nd I will leave Riverside and visit Christopher Lee in Los Angeles. I returned to Singapore on Tuesday May 24, Lisa was in Erlangen May 18 - 27, 2011.

Energy, the environment, and what mathematicians can do

Our heavy reliance on fossil fuels is causing two serious problems: global warming, and the decline of cheaply available oil reserves. Unfortunately the second problem will not cancel out the first. Each one individually seems extremely hard to solve, and taken together they demand a major worldwide effort starting now. After an overview of these problems, we turn to the question: what can mathematicians do to help?

Higher gauge theory, division algebras and superstrings

Classically, superstrings make sense when spacetime has dimension 3, 4, 6, or 10. It is no coincidence that these numbers are two more than 1, 2, 4, and 8, which are the dimensions of the normed division algebras: the real numbers, complex numbers, quaternions and octonions. We sketch an explanation of this already known fact and its relation to "higher gauge theory". Just as gauge theory describes the parallel transport of supersymmetric particles using Lie supergroups, higher gauge theory describes the parallel transport of superstrings using "Lie 2-supergroups". Recently John Huerta has shown that we can use normed division algebras to construct a Lie 2-supergroup extending the Poincaré supergroup when spacetime has dimension 3, 4, 6 and 10.

• Wednesday May 19, 2010 - Talk at the Einstein Chair Mathematics Seminar at CUNY, run by Dennis Sullivan. My contact person has been Aron Fischer. I flew to New York on Tuesday May 18th and stay at Sullivan's apartment, then leave for London on Saturday May 22nd.

  Electrical Circuits

  While category theory has many sophisticated applications to theoretical physics — especially quantum fields and strings — it also has interesting applications to a seemingly more pedestrian topic: electrical circuits. The pictorial resemblance between circuit diagrams and Feynman diagrams is an obvious clue, but what is the underlying mathematics? This question quickly leads us to an interesting combination of category theory, symplectic geometry, complex analysis and graph theory. Moreover, electrical circuits are just one example of 'open systems': physical systems that that interact with their environment. While textbooks on classical mechanics usually focus on closed systems, open systems are more important in engineering, and their mathematics is arguably deeper and more interesting.

• May 22nd, 2010 - I took a flight from JFK to Heathrow leaving at 10:30 pm and arriving at 10:30 am Sunday May 23rd. I took the Airline (a one-hour bus ride) to Oxford and went to the Cotswold Lodge, 66a Banbury Road. Then from May 24th to 28th I attended the school on Foundational Structures in Quantum Computation and Information, run by Bob Coecke and Ross Duncan. I talked to Tim Palmer over lunch on Tuesday the 24th, Thomas Fischbacher on Thursday the 27th starting at 12:00, and also Dan Ghica.

• Saturday/Sunday May 29-30, 2010 - I gave a talk at the Quantum Physics and Logic workshop at Oxford, organized by Bob Coecke, Prakash Panangaden, and Peter Selinger. Then I caught a flight from Heathrow to Los Angeles at 3:45 pm on Monday May 31st.

  Duality in Logic and Physics

  Duality has many manifestations in logic and physics. In classical logic, propositions form a partially ordered set and negation is an order-reversing involution which switches "true" and "false". The same holds in quantum logic, with propositions corresponding to closed subspaces of a Hilbert space. But the full structure of quantum physics involves more: at the very least, the category of Hilbert spaces and bounded linear operators. This category has another kind of duality, a contravariant involution that switches "preparation" and "observation". Other closely related dualities in quantum physics include "charge conjugation" (switching matter and antimatter), "parity" (switching left and right), and "time reversal" (switching future and past). The quest to find a unified mathematical framework for dualities in logic and physics leads to a fascinating variety of structures: star-autonomous categories, n-categories with duals, and more. We give a tour of these, with an effort to focus on conceptual rather than technical issues.

5

Different numbers have different personalities. The number 5 is quirky and intriguing, thanks in large part to its relation with the golden ratio, the "most irrational" of irrational numbers. The plane cannot be tiled with regular pentagons, but there exist quasiperiodic planar patterns with pentagonal symmetry of a statistical nature, first discovered by Islamic artists in the 1600s, later rediscovered by the mathematician Roger Penrose in the 1970s, and found in nature in 1984.

The Greek fascination with the golden ratio is probably tied to the dodecahedron. Much later, the symmetry group of the dodecahedron was found to give rise to a 4-dimensional regular polytope, the 120-cell, which in turn gives rise to the Poincaré homology sphere and the root system of the exceptional Lie group E₈. So, a wealth of exceptional objects arise from the quirky nature of 5-fold symmetry.

Physics, Topology, Logic and Computation: a Rosetta Stone

In particle physics, Feynman diagrams are used to reason about quantum processes. Similar diagrams can be used to reason about logic, where they represent proofs, and computation, where they represent programs. With the rise of interest in quantum cryptography and quantum computation, the explanation became clear: there is extensive network of analogies between physics, topology, logic and computation. In this introductory talk I, will make some of these analogies precise using a wonderfully general branch of mathematics called category theory.

8

The number 8 plays a special role in mathematics due to the "octonions", an 8-dimensional number system where one can add, multiply, subtract and divide, but where the commutative and associative laws for multiplication — ab = ba and (ab)c = a(bc) — fail to hold. The octonions were discovered by Hamilton's friend John Graves in 1843 after Hamilton told him about the "quaternions". While much neglected, they stand at the crossroads of many interesting branches of mathematics and physics. For example, superstring theory works in 10 dimensions because 10 = 8+2: the 2-dimensional worldsheet of a string has 8 extra dimensions in which to wiggle around, and the theory crucially uses the fact that these 8 dimensions can be identified with the octonions. Or: the densest known packing of spheres in 8 dimensions arises when the spheres are centered at certain "integer octonions", which form the root lattice of the exceptional Lie group E₈. The octonions also explain the curious way in which topology in dimension n resembles topology in dimension n+8.

Who Discovered the Icosahedron?

It has been suggested that the regular icosahedron, not being found in nature, is the first example of a geometrical object that is the free creation of human thought. Regardless of the truth of this, it is interesting to try to track down the origin of the icosahedron. A scholium in Book XIII of Euclid's "Elements" speaks of "the five so-called Platonic figures which, however, do not belong to Plato, three of the five being due to the Pythagoreans, namely the cube, the pyramid, and the dodecahedron, while the octahedron and the icosahedron are due to Theaetetus." More recently, Atiyah and Sutcliffe have claimed that a regular icosahedron appears among a collection of stone balls in the Ashmolean Museum - balls that were unearthed in Scotland and may date back to 2000 BC. However, Lieven le Bruyn has argued that these authors are the victims of a hoax. We examine the evidence with a critical eye.

Categorification in Fundamental Physics

Categorification is the process of replacing set-based mathematics with analogous mathematics based on categories or n-categories. In physics, categorification enters naturally as we pass from the mechanics of particles to higher-dimensional field theories. For example, higher gauge theory is a generalization of gauge theory that describes the parallel transport not just of particles, but also strings or higher-dimensional branes. To handle strings, we must categorify familiar notions from gauge theory and consider connections on "principal 2-bundles" with a given "structure 2-group". One of the simplest 2-groups is the shifted version of U(1). U(1) gerbes are really principal 2-bundles with this structure 2-group, and the B field in string theory can be seen as a connection on this sort of 2-bundle. The relation between U(1) bundles and symplectic manifolds, so important in the geometric quantization, extends to a relation between U(1) gerbes and "2-plectic manifolds", which arise naturally as phase spaces for 2-dimensional field theories, such as the theory of a classical string. More interesting 2-groups include the "string 2-group" associated to a compact simple Lie group G. This is built using the central extension of the loop group of G. A closely related 3-group plays an important role in Chern-Simons theory, and it appears that n-groups for higher n are important in the study of higher-dimensional membranes.

1. Connections on abelian gerbes
2. Lie n-groups and Lie n-algebras
3. Multisymplectic geometry and classical field theory
4. Higher gauge theory and the string 2-group
5. Higher gauge theory, strings and branes

I took a flight from Ontario Airport to Dallas-Forth Worth on Monday September 7th, leaving at 3:20 pm and arriving at 8:10 pm. I came back on Thursday the 10th at 9:15 pm.

At 1 pm on Tuesday the 8th I spoke about the number 5.

At 7 pm on Tuesday the 8th I spoke about Zooming Out in Time.

At 1 pm on Wednesday the 9th I spoke about the number 8.

At 4 pm on Wednesday the 9th I spoke about Fundamental Physics: Where We Stand Today.

At 1 pm on Thursday the 10th I spoke about the number 24.

Computation and the Periodic Table

In physics, Feynman diagrams are used to reason about quantum processes. Similar diagrams can also be used to reason about logic, where they represent proofs, and computation, where they represent programs. With the rise of topological quantum field theory and quantum computation, it became clear that diagrammatic reasoning takes advantage of an extensive network of interlocking analogies between physics, topology, logic and computation. These analogies can be made precise using the formalism of symmetric monoidal closed categories. But symmetric monoidal categories are just the n = 1, k = 3 entry of a hypothesized "periodic table" of k-tuply monoidal n-categories. This raises the question of how these analogies extend. An important clue comes from the way symmetric monoidal closed 2-categories describe rewrite rules in the lambda calculus and multiplicative intuitionistic linear logic. This talk is based on work in progress with Paul-André Melliès and Mike Stay.

Why Smooth Spaces?

The category of smooth manifolds and smooth maps is often taken as the default context for research on differential geometry. However, in many applications it is convenient or even necessary to work in a more general framework. In this introductory talk we explain various reasons for this. We also describe the advantages of various alternative frameworks, including Banach manifolds and other types of infinite-dimensional manifolds, Chen spaces and diffeological spaces, orbifolds and differentiable stacks, and synthetic differential geometry.

Categorification and Topology

The relation between n-categories and topology is clarified by a collection of hypotheses, some of which have already been made precise and proved. The "homotopy hypothesis" says that homotopy n-types are the same as n-groupoids. The "stabilization hypothesis" says that each column in the periodic table of n-categories stabilizes at a certain precise point. The "cobordism hypothesis" gives an n-categorical description of cobordisms, while the "tangle hypothesis" does the same for tangles and their higher-dimensional relatives. We shall sketch these ideas, describe recent work by Lurie and Hopkins on the cobordism and tangle hypotheses, and, time permitting, say a bit about how these ideas are related to other lines of work on categorification.

Lectures on Higher Gauge Theory

Gauge theory describes the parallel transport of point particles using the formalism of connections on bundles. In both string theory and loop quantum gravity, point particles are replaced by 1-dimensional extended objects: paths or loops in space. This suggests that we seek some sort of "higher gauge theory" that describes parallel transport as we move a path through space, tracing out a surface. To find the right mathematical language for this, we must "categorify" concepts from topology and geometry, replacing smooth manifolds by smooth categories, Lie groups by Lie 2-groups, Lie algebras by Lie 2-algebras, bundles by 2-bundles, sheaves by stacks or gerbes, and so on. This overview of higher gauge theory will emphasize its relation to homotopy theory and the cohomology of groups and Lie algebras.

• Lecture 1 - Lie 2-groups and Lie 2-algebras. 2-3 pm, Thursday February 5th.
• Lecture 2 - 2-bundles and classifying spaces for 2-groups. 9-10 am, Friday February 6th.
• Lecture 3 - 2-connections on 2-bundles. 3-4 pm, Friday February 6th.

I gave a talk at the special session on Homotopy Theory and Higher Categories run by Tom Fiore, Mark Johnson, Jim Turner, Steve Wilson and Donald Yau. This was on Wednesday January 7th, 1-1:20 pm in Virginia Suite C, Lobby Level, Marriott:

Classifying Spaces for Topological 2-Groups

Categorifying the concept of topological group, one obtains the notion of a topological 2-group. This in turn allows a theory of "principal 2-bundles" generalizing the usual theory of principal bundles. It is well-known that under mild conditions on a topological group G and a space M, principal G-bundles over M are classified by either the Cech cohomology H¹(M,G) or the set of homotopy classes [M,BG], where BG is the classifying space of G. Here we review work by Bartels, Jurco, Baas-Bökstedt-Kro, Stevenson and myself generalizing this result to topological 2-groups. We explain various viewpoints on topological 2-groups and the Cech cohomology H¹(M,G) with coefficients in a topological 2-group G, also known as "nonabelian cohomology". Then we sketch a proof that under mild conditions on M and G there is a bijection between H¹(M,G) and [M,B|NG|], where B|NG| is the classifying space of the geometric realization of the nerve of G.

I also gave a talk at the special session on Categorification and Link Homology, run by Aaron Lauda and Mikhail Khovanov. This was on Wednesday January 7th, 5:10 - 5:30 pm, in the Harding Room, Mezzanine Level, Marriott:

Groupoidification

There is a systematic process that turns groupoids into vector spaces and spans of groupoids into linear operators. "Groupoidification" is the attempt to reverse this process, taking familiar structures from linear algebra and enhancing them to obtain structures involving groupoids. Like quantization, groupoidification is not entirely systematic. However, examples show that it is a good thing to try! For example, groupoidifying the quantum harmonic oscillator yields combinatorial structures associated to the groupoid of finite sets, while groupoidifying the q-deformed oscillator yields structures associated to finite-dimensional vector spaces over the field with q elements. Starting with flag varieties defined over the field with q elements, we can also groupoidify Hecke and Hall algebras.

Groupoidification

There is a systematic process that turns groupoids into vector spaces and spans of groupoids into linear operators. "Groupoidification" is the attempt to reverse this process, taking familiar structures from linear algebra and enhancing them to obtain structures involving groupoids. Like quantization, groupoidification is not entirely systematic. However, examples show that it is a good thing to try! For example, groupoidifying the quantum harmonic oscillator yields combinatorial structures associated to the groupoid of finite sets. We can also groupoidify mathematics related to quantum groups - for example, Hecke algebras and Hall algebras. It turns out that we obtain structures related to algebraic groups defined over finite fields. After reviewing the basic idea of groupoidification, we shall describe as many examples as time permits.

8

Different numbers have different personalities, and 8 is one of my favorites. The number 8 plays a special role in mathematics due to the "octonions", an 8-dimensional number system where one can add, multiply, subtract and divide, but multiplication is noncommutative and nonassociative. The octonions were discovered by Hamilton's friend John Graves in 1843 after Hamilton told him about the "quaternions". While much neglected, they stand at the crossroads of many interesting branches of mathematics and physics. For example, superstring theory works in 10 dimensions because 10 = 8+2, where 8 is the dimension of the octonions. Also, the densest known packing of spheres in 8 dimensions occurs when the spheres are centered at certain "integer octonions", which form the root lattice of the exceptional Lie group E8. The octonions also explain the curious way in which topology in dimension n resembles topology in dimension n+8.

Higher Gauge Theory and the String Group

Higher gauge theory is a generalization of gauge theory that describes the parallel transport not just of particles, but also strings or higher-dimensional branes. To handle strings, one can categorify familiar notions from gauge theory and consider "principal 2-bundles" with a given "structure 2-group". These are a slight generalization of nonabelian gerbes. We focus on examples related to the 2-group String_k(G) associated to any compact simple Lie group G. We describe how this 2-group is built using the level-k central extension of the loop group of G, and how it is related to the "string group". Finally, we discuss 2-bundles with String_k(G) as structure 2-group, and characteristic classes for these 2-bundles.

The overall title will be My Favorite Numbers and individual titles "5", "8", and "24". These talks will be written up and published with some help from the Trust.

5 (Monday September 15th, 4 pm)

Different numbers have different personalities. The number 5 is quirky and intriguing, thanks in large part to its relation with the golden ratio, the "most irrational" of irrational numbers. The plane cannot be tiled with regular pentagons, but there exist quasiperiodic planar patterns with pentagonal symmetry of a statistical nature, first discovered by Islamic artists in the 1600s, later rediscovered by the mathematician Roger Penrose in the 1970s, and found in nature in 1984. The Greek fascination with the golden ratio is probably tied to the dodecahedron. Much later, the symmetry group of the dodecahedron was found to give rise to a 4-dimensional regular polytope, the 120-cell, which in turn gives rise to the Poincaré homology sphere and the root system of the exceptional Lie group E₈. So, a wealth of exceptional objects arise from the quirky nature of 5-fold symmetry.

8 (Wednesday September 17th, 4 pm)

The number 8 plays a special role in mathematics due to the "octonions", an 8-dimensional number system where one can add, multiply, subtract and divide, but where the commutative and associative laws for multiplication — ab = ba and (ab)c = a(bc) — fail to hold. The octonions were discovered by Hamilton's friend John Graves in 1843 after Hamilton told him about the "quaternions". While much neglected, they stand at the crossroads of many interesting branches of mathematics and physics. For example, superstring theory works in 10 dimensions because 10 = 8+2: the 2-dimensional worldsheet of a string has 8 extra dimensions in which to wiggle around, and the theory crucially uses the fact that these 8 dimensions can be identified with the octonions. Or: the densest known packing of spheres in 8 dimensions arises when the spheres are centered at certain "integer octonions", which form the root lattice of the exceptional Lie group E₈. The octonions also explain the curious way in which topology in dimension n resembles topology in dimension n+8.

24 (Friday September 19th, 4 pm)

The numbers 12 and 24 play a central role in mathematics thanks to a series of "coincidences" that is just beginning to be understood. One of the first hints of this fact was Euler's bizarre "proof" that

1 + 2 + 3 + 4 + ... = -1/12

which he obtained before Abel declared that "divergent series are the invention of the devil". Euler's formula can now be understood rigorously in terms of the Riemann zeta function, and in physics it explains why bosonic strings work best in 26=24+2 dimensions. The fact that

1² + 2² + 3² + ... + 24²

is a perfect square then sets up a curious link between string theory, the Leech lattice (the densest known way of packing spheres in 24 dimensions) and a group called the Monster. A better-known but closely related fact is the period-12 phenomenon in the theory of "modular forms". We shall do our best to demystify some of these deep mysteries.

• July 7-11, 2008 - Algebraic Topological Methods in Computer Science 2008 at University of Paris Diderot (Paris 7). I gave this one-hour plenary talk at 2:30-3:30 pm on Monday July 7th:

  Computation and the Periodic Table

  By now there is an extensive network of interlocking analogies between physics, topology, logic and computer science, which can be seen most easily by comparing the roles that symmetric monoidal closed categories play in each subject. However, symmetric monoidal categories are just the n = 1, k = 3 entry of a hypothesized "periodic table" of k-tuply monoidal n-categories. This raises the question of how these analogies extend. We present some thoughts on this question, focusing on how symmetric monoidal closed 2-categories might let us understand the lambda calculus more deeply.

• Sunday July 13 - Wednesday July 16, 2008 - Visit to Lisbon, Portugal for the agregãço of Alexsandar Mikovic, which will be from 2-4 pm on Monday the 14th and Tuesday the 15th, with some bureacratic stuff lasting until 5 pm on Tuesday. I'm giving a talk on Classifying Spaces for Topological 2-Groups on Monday morning. Invited by Roger Picken.

• Thursday July 24 - Talk on "Groupoidification" at the Preuves, Programmes et Systemes group at Université Paris 7.

I stayed at the SERHS Campus Hotel on the campus of the Universitat Autonoma de Barcelona (UAB) campus in Bellaterra, 18 km north of Barcelona. This campus is where the CRM is located.

I gave the first talk, at 9:30 am on Monday June 30th:

Groupoidification

There is a systematic process that turns groupoids into vector spaces and spans of groupoids into linear operators. "Groupoidification" is the attempt to reverse this process, taking familiar structures from linear algebra and enhancing them to obtain structures involving groupoids. Like quantization, groupoidification is not entirely systematic. However, examples show that it is a good thing to try! For example, groupoidifying the quantum harmonic oscillator yields combinatorial structures associated to the groupoid of finite sets. Groupoidifying the q-deformed oscillator yields combinatorial structures associated to finite-dimensional vector spaces over the field with q elements. We can also groupoidify some mathematics related to quantum groups and representations of finite groups. We first describe the basic ideas, and then as many examples as time permits.

An overall map is here. I stayed at the residence Carmen de la Victoria, 9 Cuesta del Chapiz, from June 21st to 29th. On Sunday the 29th my flight left for Barcelona at 8:45 am.

Here's an overall map.

I stayed at the Residència d'Investigadors, Carrer de l'Hospital, 64 08001 Barcelona.

The IMUB is here, inside the Facultat de Mathemàtiques in the historic building of the Universitàt de Barcelona, at Gran Via 585. The morning lectures took place in Aula B6 (that's in the north-most corner of the building), while the afternoon lectures took place in the "Aula Aribau" (that's in the south-most corner, in fact in the modern building just next to the historical building).

I gave a talk on Monday June 16th, starting at 10 am: first 1 hour of background, then 45 minutes of actual talk, then 45 minutes for discussion.

Topological 2-Groups and Their Classifying Spaces

Categorifying the concept of topological group, one obtains the notion of a topological 2-group. This in turn allows a theory of "principal 2-bundles" generalizing the usual theory of principal bundles. It is well-known that under mild conditions on a topological group G and a space M, principal G-bundles over M are classified by either the Cech cohomology H¹(M,G) or the set of homotopy classes [M,BG], where BG is the classifying space of G. Here we review work by Bartels, Jurco, Baas-Bökstedt-Kro, and others generalizing this result to topological 2-groups. We explain various viewpoints on topological 2-groups and the Cech cohomology H¹(M,G) with coefficients in a topological 2-group G, also known as "nonabelian cohomology". Then we sketch a proof that under mild conditions on M and G there is a bijection between H¹(M,G) and [M,B|G|], where B|G| is the classifying space of the geometric realization of the nerve of G.

• Tuesday May 20, 2008 - Talk at the Groupoids in Analysis and Geometry seminar at U. C. Berkeley - visit organized by Alan Weinstein.

  Groupoidification

  There is a systematic process that turns groupoids into vector spaces and spans of groupoids into linear operators. "Groupoidification" is the attempt to reverse this process, taking familiar structures from linear algebra and enhancing them to obtain structures involving groupoids. Like quantization, groupoidification is not entirely systematic. However, examples show that it is a good thing to try! For example, groupoidifying the quantum harmonic oscillator yields combinatorial structures associated to the groupoid of finite sets. Groupoidifying the q-deformed oscillator yields combinatorial structures associated to finite-dimensional vector spaces over the field with q elements. We can also groupoidify some mathematics related to quantum groups and representations of finite groups. We first describe the basic ideas, and then as many examples as time permits.

• Thursday May 22nd, 2008 - Talk on "5" at Google headquarters in Mountain View, hosted by Mike Stay.

5

Different numbers have different personalities. The number 5 is quirky and intriguing, thanks in large part to its relation with the golden ratio, the "most irrational" of irrational numbers. The plane cannot be tiled with regular pentagons, but there exist quasiperiodic planar patterns with pentagonal symmetry of a statistical nature, first discovered by Islamic artists in the 1600s, later rediscovered by the mathematician Roger Penrose in the 1970s, and found in nature in 1984. The Greek fascination with the golden ratio is probably tied to the dodecahedron. Much later, the symmetry group of the dodecahedron was found to give rise to a 4-dimensional regular polytope, the 120-cell, which in turn gives rise to the Poincaré homology sphere and the root system of the exceptional Lie group E₈. So, a wealth of exceptional objects arise from the quirky nature of 5-fold symmetry.

Higher Gauge Theory

Higher gauge theory is a generalization of gauge theory that describes the parallel transport not just of particles, but also strings or higher-dimensional branes. To handle strings, we generalize familiar notions from gauge theory and consider connections on "2-bundles" with a given "structure 2-group". After an introduction to these ideas, we discuss one of the most interesting 2-groups: the "string 2-group" associated to any compact simple Lie group G. This 2-group is built using a central extension of the loop group of G. We describe the theory of characteristic classes for 2-bundles with this structure 2-group.

• Thursday the 1st, 6 pm: public talk:

  Zooming Out in Time: A Long Term History of Climate Change

  How can we detect and understand oncoming crises in time to avert them? Sometimes we must "zoom out": expand our perspective and find similar situations in the distant past. A good example is climate change. What can a few degrees of warming do? To answer this, we need to know some history: how the Earth's climate has changed over the last 65 million years.

• Friday the 2nd, around noon: lunchtime chalk talk on mathematical physics.
• Friday the 2nd, 3:45-4:45: departmental colloquium:

  Fundamental Physics: Where We Stand Today

  Since the discovery of the W and Z particles over twenty years ago, few truly novel predictions of fundamental theoretical physics have been confirmed by experiment. On the other hand, observations in astronomy have revealed shocking facts that our theories do not really explain: most of our universe consists of "dark matter" and "dark energy". Where does fundamental physics stand today, and why has theory become divorced from experiment?

I went on Wednesday October 31st and came back on Monday November 5th after spending a weekend in Great Falls visiting my parents.

Spans in Quantum Theory

Many features of quantum theory — quantum teleportation, violations of Bell's inequality, the no-cloning theorem and so on — become less puzzling when we realize that quantum processes more closely resemble pieces of spacetime than functions between sets. In the language of category theory, the reason is that Set is a "cartesian" category, while the category of finite-dimensional Hilbert spaces, like a category of cobordisms describing pieces of spacetime, is "dagger compact". Here we discuss a possible explanation for this curious fact. We recall the concept of a "span", and show how categories of spans are a generalization of Heisenberg's matrix mechanics. We explain how the category of Hilbert spaces and linear operators resembles a category of spans, and how cobordisms can also be seen as spans. Finally, we sketch a proof that whenever C is a cartesian category with pullbacks, the category of spans in C is dagger compact.

• August 5-10, 2007 - the fourth Abel Symposium in Oslo, Norway. This symposium was organized by Eric Friedlander, Stefan Schwede and Graeme Segal together with the local representatives Nils Baas, Bjørn Ian Dundas, Bjørn Jahren and John Rognes. It covered the following aspects of modern algebraic topology:

  • algebraic K-theory and motivic homotopy theory
  • structured ring spectra and homotopical algebraic geometry
  • elliptic objects and quantum field theory

  My talk was on Wednesday the 8th at 11 am:

  Higher Gauge Theory and Elliptic Cohomology

  The concept of elliptic object suggests a relation between elliptic cohomology and "higher gauge theory", a generalization of gauge theory describing the parallel transport of strings. In higher gauge theory, we categorify familiar notions from gauge theory and consider "principal 2-bundles" with a given "structure 2-group". These are a slight generalization of nonabelian gerbes. After a quick introduction to these ideas, we focus on the 2-groups String_k(G) associated to any compact simple Lie group G. We describe how these 2-groups are built using central extensions of the loop group ΩG, and how the classifying space for String_k(G)-2-bundles is related to the "string group" familiar in elliptic cohomology. If there is time, we shall also describe a vector 2-bundle canonically associated to any principal 2-bundle, and how this relates to the von Neumann algebra construction of Stolz and Teichner.

• August 18-26, 2007 - visit to the Erwin Schrödinger Institut in Vienna, to attend a Workshop on Poisson Geometry and Sigma Models organized by Anton Alekseev, Henrique Bursztyn and Thomas Strobl, which lasts from August 20th to 24th. I have a reservation at the Pension ANI, Kinderspitalgasse 1, 9th district - arriving on Saturday the 18th and leaving on Sunday the 26th.

  I gave my talk at 9 am on Wednesday August 22nd:

  Higher Gauge Theory and the String Group

  Higher gauge theory is a generalization of gauge theory that describes the parallel transport not just of particles, but also strings or higher-dimensional branes. To handle strings, we categorify familiar notions from gauge theory and consider "principal 2-bundles" with a given "structure 2-group". These are a slight generalization of nonabelian gerbes. We focus on examples related to the 2-group String_k(G) associated to any compact simple Lie group G. We describe how this 2-group is built using the level-k central extension of the loop group of G, and how it is related to the "string group". Finally, we discuss 2-bundles with String_k(G) as structure 2-group, and pose the problem of computing characteristic classes for such 2-bundles in terms of connections.

• September 4, 2007 - talk at the London Analysis and Probability Seminar, University College, London:

  2-Hilbert Spaces

  In work inspired by topological quantum field theory, Kapranov and Voevodsky found it useful to "categorify" the concept of a finite-dimensional vector space and invent the concept of "2-vector space". In simple terms, this amounts to replacing vectors - viewed as lists of numbers - by "2-vectors", which are lists of vector spaces. For purposes of analysis it is important to go further and find a good notion of "2-Hilbert space". For example, just as the category of finite-dimensional representations of a finite group is a 2-vector space, the category of unitary representations of a Lie group should be a 2-Hilbert space. We sketch some attempts to define 2-Hilbert spaces using measurable fields of Hilbert spaces.

• September 10-12, 2007 - 22nd British Topology Meeting at Sheffield University. I gave my talk on 4 pm on Monday September 10th:

  Higher Gauge Theory and the String Group

  Higher gauge theory is a generalization of gauge theory that describes the parallel transport not just of particles, but also strings or higher-dimensional branes. To handle strings, we categorify familiar notions from gauge theory and consider "principal 2-bundles" with a given "structure 2-group". These are a slight generalization of nonabelian gerbes. We focus on examples related to the 2-group String_k(G) associated to any compact simple Lie group G. We describe how this 2-group is built using the level-k central extension of the loop group of G, and how it is related to the "string group". Finally, we discuss 2-bundles with String_k(G) as structure 2-group, and pose the problem of computing characteristic classes for such 2-bundles in terms of connections.

Why Mathematics is Boring

Storytellers have many strategies for luring in their audience and keeping them interested. These include standardized narrative structures, vivid characters, breaking down long stories into episodes, and subtle methods of reminding the readers of facts they may have forgotten. The typical style of writing mathematics systematically avoids these strategies, since the explicit goal is "proving a fact" rather than "telling a story". Readers are left to provide their own narrative framework, which they do privately, in conversations, or in colloquium talks. As a result, even expert mathematicians find papers - especially those outside their own field - boring and difficult to understand. This impedes the development of mathematics. In my attempts at mathematics exposition I have tried to tackle this problem by using some strategies from storytelling, which I illustrate here.

• Tuesday July 10th - talk at the AstroParticule et Cosmologie (APC) group at Université Paris 7, invited by Marc Lachièze-Rey. The talk will be at 2 pm.

  Cartan Geometry and MacDowell–Mansouri Gravity: the Work of Derek Wise

  MacDowell and Mansouri invented a clever formulation of general relativity in which the Lorentz connection and coframe field are combined into a single connection with the DeSitter group SO(4,1) or anti-DeSitter group SO(3,2) as gauge group, depending on the sign of the cosmological constant. While this formulation may seem like a 'trick', it actually has a deep geometrical meaning. This is best understood in terms of Cartan's approach to connections — an approach which was somewhat forgotten after his student Ehresmann developed the simpler approach that eventually became standard. Witten's formulation of 3d gravity as a Chern-Simons theory is also clarified using Cartan geometry. However, in 3 dimensions the relevant Cartan connection is flat and gravity is a topological field theory, while in 4 dimensions this is true only in a certain limit. In this limit, point particles and certain string-like excitations can be nicely described as topological defects. This talk is an exposition of the work of Derek Wise.

Quantum Quandaries: a Category-Theoretic Perspective

Category theory is a general language for describing things and processes - called "objects" and "morphisms". In this language, the counterintuitive features of quantum theory turn out to be properties that the category of Hilbert spaces shares with the category of cobordisms - in which objects are choices of "space", and morphisms are choices of "spacetime". In particular, both these categories - but not the category of sets and functions - are noncartesian monoidal categories with duals. We show how this accounts for many of the famously puzzling features of quantum theory: the failure of local realism, the impossibility of duplicating quantum information, and so on. We argue that these features only seem puzzling when we try to treat the category of Hilbert spaces as analogous to the category of sets rather than the category of cobordisms, so that quantum theory will make more sense when regarded as part of a theory of spacetime. To find such a theory, it may be helpful to study categories of "spans" and "cospans".

The actual conference was from Tuesday April 24nd to Friday April 27th, but I flew there on Sunday April 22nd, arriving at Nice airport on Monday April 23rd. I left the conference on the morning of Saturday April 28th, spent a day in Nice visiting Eugenia Cheng, and departed from Nice airport on Sunday morning.

I arrived January 6th and left January 15th. On Wednesday January 10th I gave this talk:

The Homotopy Hypothesis

Crudely speaking, the Homotopy Hypothesis says that n-groupoids are the same as homotopy n-types - nice spaces whose homotopy groups above the nth vanish for every basepoint. We summarize the evidence for this hypothesis. Naively, one might imagine this hypothesis allows us to reduce the problem of computing homotopy groups to a purely algebraic problem. While true in principle, in practice information flows the other way: established techniques of homotopy theory can be used to study coherence laws for n-groupoids, and a bit more speculatively, n-categories in general.

Higher Gauge Theory

Gauge theory describes the parallel transport of point particles using the formalism of connections on bundles. In both string theory and loop quantum gravity, point particles are replaced by 1-dimensional extended objects: paths or loops in space. This suggests that we seek some sort of "higher gauge theory" that describes parallel transport as we move a path through space, tracing out a surface. To find the right mathematical language for this, we must "categorify" concepts from topology and geometry, replacing Lie groups by Lie 2-groups, bundles by 2-bundles, and so on. Some interesting examples of these concepts show up in the mathematics of topological quantum field theory, string theory and 11-dimensional supergravity.

Higher Gauge Theory

Gauge theory describes the parallel transport of point particles using the formalism of connections on bundles. In both string theory and loop quantum gravity, point particles are replaced by 1-dimensional extended objects: paths or loops in space. This suggests that we seek some sort of "higher gauge theory" that describes parallel transport as we move a path through space, tracing out a surface. To find the right mathematical language for this, we must "categorify" concepts from topology and geometry, replacing Lie groups by Lie 2-groups, bundles by 2-bundles, and so on. Some interesting examples of these concepts show up in the mathematics of topological quantum field theory, string theory and 11-dimensional supergravity.

Tales of the Dodecahedron: from Pythagoras through Plato to Poincaré

The dodecahedron is a beautiful shape made of 12 regular pentagons. It doesn't occur in nature; it was invented by the Pythagoreans, and we first read of it in a text written by Plato. We shall see some of its many amazing properties: its relation to the Golden Ratio, its rotational symmetries — and best of all, how to use it to create a regular solid in 4 dimensions! Poincaré exploited this to invent a 3-dimensional space that disproved a conjecture he made. This led him to an improved version of his conjecture, which was recently proved by the reclusive Russian mathematician Grigori Perelman — who now stands to win a million dollars.

Zooming Out in Time

How can we detect and understand oncoming crises in time to avert them? Sometimes we must "zoom out": expand our perspective and find similar situations in the distant past. A good example is climate change. What can a few degrees of warming do? To answer this, we need to know some history: how the Earth's climate has changed over the last 65 million years.

• August 18-21, 2006 - Suzhou.
• September 14-17, 2006 - Hangzhou.

• Wednesday, May 31, 2006 - I gave this week's colloquium at the Perimeter Institute at 2 pm:

  Higher-Dimensional Algebra: A Language for Quantum Spacetime

  Category theory is a general language for describing things and processes - called "objects" and "morphisms". In this language, the counterintuitive features of quantum theory turn out to be properties that the category of Hilbert spaces shares with the category of cobordisms - in which objects are choices of "space", and morphisms are choices of "spacetime". The striking similarities between these categories suggests that "n-categories with duals" are a promising framework for a quantum theory of spacetime. We sketch the historical development of these ideas from Feynman diagrams, to string theory, topological quantum field theory, spin networks and spin foams, and especially recent work on open-closed string theory, quantum gravity coupled to point particles, and 4d BF theory coupled to strings.

• Thursday, June 1, 2006 - I gave a colloquium in the mathematics department at the University of Western Ontario at 3:30-4:30 pm, after coffee at 3.

  Fundamental Physics: Where We Stand Today

  Since the discovery of the W and Z particles over twenty years ago, no really novel prediction of fundamental theoretical physics has been confirmed by experiment, except perhaps Guth's inflationary cosmology. On the other hand, observations in astronomy have revealed shocking new facts which our theories do not really explain: most of our universe consists of "dark matter" and "dark energy". Where does fundamental physics stand today, and why has theory become divorced from experiment?

• I visited Cambridge Massachusetts on June 2-6 (Friday-Tuesday), reading grant proposals.

• I visited my parents in DC on June 6-11 (Tuesday-Sunday).

• Back at Waterloo June 11th-20th (Sunday-Tuesday). Talk with Howard Burton at 11 am on Wednesday the 14th.

• Tuesday June 20th: back to Riverside.

• April 7-11, 2006 - I attended the Mac Lane Memorial Conference at the University of Chicago. In conjunction with this, I gave the 24th annual Unni Namboodiri Lectures - a series of three lectures at 4 pm on the 7th (Friday), 4 pm on the 10th (Monday), and 4:30 pm on the 11th (Tuesday):

  Higher Gauge Theory, Higher Categories

  The work of Eilenberg and Mac Lane marks the beginning of a trend in which mathematics based on sets is generalized to mathematics based on categories and then higher categories. We illustrate this trend towards "categorification" by a detailed introduction to "higher gauge theory".

  Gauge theory describes the parallel transport of point particles using the formalism of connections on bundles. In both string theory and loop quantum gravity, point particles are replaced by 1-dimensional extended objects: paths or loops in space. This suggests that we seek some kind of "higher gauge theory" that describes the parallel transport as we move a path through space, tracing out a surface. Surprisingly, this requires that we "categorify" concepts from differential geometry, replacing smooth manifolds by smooth categories, Lie groups by Lie 2-groups, Lie algebras by Lie 2-algebras, bundles by 2-bundles, sheaves by stacks or gerbes, and so on.

  To explain how higher gauge theory fits into mathematics as a whole, we start with a lecture reviewing the basic principle of Galois theory and its relation to Klein's Erlangen program, covering spaces and the fundamental group, Eilenberg-Mac Lane spaces, and Grothendieck's ideas on fibrations.

  The second lecture treats connections on trivial bundles and 2-connections on trivial 2-bundles, explaining how they can be described either in terms of their holonomies or in terms of Lie-algebra-valued differential forms. For a clean treatment of these concepts, we recall Chen's theory of "smooth spaces", which generalize smooth finite-dimensional manifolds.

  The third lecture explains connections on general bundles and 2-connections on general 2-bundles, explaining how they can be described either in terms of holonomies or local data involving differential forms. We also explain how 2-bundles are described using nonabelian Cech 2-cocycles, and how the theory of 2-connections relates to Breen and Messing's theory of "connections on nonabelian gerbes".

• Starting Wednesday April 19th, I gave a series of informal talks to the category theorists at the University of Chicago, about topics that may be covered in my book:
  • On Wednesday April 19th, at 2:30 pm, room E203: The Power of Negative Thinking
  • On Friday April 21st, at 2:30 pm, room E312: Cohomology: The Layer-Cake Philosophy
  • On Monday April 24th, at 3:00 pm, room E203: An Example: Classifying 2-Groupoids

  Michael Shulman took notes on these talks and wrote an extensive appendix on topos theory.

• April 29-May 1, 2006 - three 1-hour talks at the 2006 Barrett Lectures, a conference on geometric topology at the University of Tennessee in Knoxville. I left on Friday April 28th, and returned on Wednesday May 3rd.

  Higher Gauge Theory

  Gauge theory describes the parallel transport of point particles using the formalism of connections on bundles. In both string theory and loop quantum gravity, point particles are replaced by 1-dimensional extended objects: paths or loops in space. This suggests that we seek some sort of "higher gauge theory" that describes parallel transport as we move a path through space, tracing out a surface. To find the right mathematical language for this, we must "categorify" concepts from topology and geometry, replacing smooth manifolds by smooth categories, Lie groups by Lie 2-groups, Lie algebras by Lie 2-algebras, bundles by 2-bundles, sheaves by stacks or gerbes, and so on. We give an overview of higher gauge theory, with an emphasis on its relation to homotopy theory and the cohomology of groups and Lie algebras.

  On May 2nd there was an excursion to the Smoky Mountains. I flew there on April 28th and flew back on May 3rd.

Loop Quantum Gravity

One of the great challenges facing physics today is to reconcile quantum theory and general relativity. Loop quantum gravity is an approach to this challenge that incorporates quantum theory into our description of spacetime from the very start. Quantum states of the geometry of space are described by "spin networks" - graphs with certain labellings of their edges and vertices. The theory predicts that geometrical quantities such as area and volume take on a discrete spectrum of possible values, and it explains the entropy of black holes by associating information to each point at which a spin network edge punctures the event horizon. This talk will be a nontechnical overview of the basic ideas behind loop quantum gravity.

Universal Algebra and Diagrammatic Reasoning

Since the introduction of category theory, the old subject of "universal algebra" has diversified into a large collection of frameworks for describing algebraic structures. These include "monads" (formerly known as "triples"), the "algebraic theories" of Lawvere, and the "PROPs" of Adams, Mac Lane, Boardman and Vogt. We give an overview of these different frameworks, which are closely related, and explain how one can reason diagrammatically about algebraic structures defined using them. Our treatment of monads focuses on the abstract "bar construction". Our treatment of algebraic theories and PROPs explains how the latter are related to Feynman diagrams, and leads up to an adjunction between algebraic theories and PROPs which is analogous to the relation between classical and quantum physics. We conclude with some reflections on how features of our physical universe have influenced our notions of universal algebra.

On Monday February 27th I gave a talk for a large scientific audience at the Faculté des Sciences de Luminy:

Fundamental Physics: Where We Stand Today

Since the discovery of the W and Z particles over twenty years ago, no really novel prediction of fundamental theoretical physics has been confirmed by experiment, except perhaps Guth's inflationary cosmology. On the other hand, observations in astronomy have revealed shocking new facts which our theories do not really explain: most of our universe consists of "dark matter" and "dark energy". Where does fundamental physics stand today, and why has theory become divorced from experiment?

During this time I also visited Carlo Rovelli and Alejandro Perez at the Centre de Physique Theorique de Luminy. Kirill Krasnov arrived on Sunday, February 26th around 1 pm, and left on Wednesday, March 1st early in the morning. We talked about his ideas on "2-Feynman diagrams" and their relation to my n-categorial approach to spin foams.

Higher Gauge Theory: 2-Connections

Gauge theory describes the parallel transport of point particles using the formalism of connections on bundles. In both string theory and loop quantum gravity, point particles are replaced by 1-dimensional extended objects: paths or loops in space. This suggests that we seek some kind of "higher gauge theory" that describes the parallel transport as we move a path through space, tracing out a surface. To find the right mathematical language for this, it seems we must "categorify" concepts from differential geometry, replacing smooth manifolds by smooth categories, Lie groups by Lie 2-groups, Lie algebras by Lie 2-algebras, bundles by 2-bundles, sheaves by stacks or gerbes, and so on. We give an overview of higher gauge theory, with an emphasis on the concept of "2-connection" for a principal 2-bundle.

home