- Part 1: introduction, definition
of smooth manifolds, smooth maps, products of manifolds, Lie groups, the
general
linear groups \(\mathrm{GL}(n,\mathbb{R})\) and
\(\mathrm{GL}(n,\mathbb{C})\), the closed
subgroup theorem, and the definition of matrix Lie
groups.
- Part 2: Lie group homomorphisms,
the category of Lie groups. Examples of matrix Lie groups:
Picturing all these groups in the case \(n = 1\).
- Part 3: Picturing some of these
groups in the case \(n = 2\). Why \(\mathrm{SO}(2) \cong
\mathrm{U}(1) \cong S^1\). Why \(\mathrm{O}(n)\) is diffeomorphic to
the disjoint union of two copies of \(\mathrm{SO}(n)\). Why
\(\mathrm{SL}(2,\mathbb{R})\) is diffeomorphic to \(\mathbb{R}^2
\times S^1\), and how \(\mathrm{SO}(2)\) sits inside
\(\mathrm{SL}(2,\mathbb{R})\). Examples of maximal compact subgroups.
Every connected Lie group \(G\) is diffeomorphic to \(K \times
\mathbb{R}^n\) for a maximal compact subgroup \(K \subseteq G\), which
is unique up to conjugation.
-
Part 4:
The three associative normed division
algebra: the real numbers \(\mathbb{R}\), the complex numbers
\(\mathbb{C}\) and the quaternions
\(\mathbb{H}\). Defining the quaternions and proving that they form a
normed division algebra. Proof that as Lie groups, \(\mathrm{SU}(2)\) is isomorphic to
$$ \mathrm{Sp}(1) = \{a \in \mathbb{H}: \; |a| = 1
\}.$$
Quaternionic
matrix groups: the quaternionic
general linear group:
$$ \mathrm{GL}(n,\mathbb{H}) = \{g \in
\mathrm{M}_n(\mathbb{H}) : \; g \textrm{ invertible} \} $$
the quaternionic special linear group:
$$ \mathrm{SL}(n,\mathbb{H}) = \{g \in
\mathrm{M}_n(\mathbb{H}) : \; \det(g) = 1 \} $$
and the quaternionic
unitary group, also called the compact symplectic group:
$$
\mathrm{Sp}(n) = \{g \in \mathrm{M}_n(\mathbb{H}) : \; gg^\ast = 1 \}
$$
A warning about quaternionic
determinants: they take values in the complex numbers, and
\(gg^\ast = 1\) implies \(\mathrm{det}(g) = 1\) so
\(\mathrm{Sp}(n,\mathbb{H}) \subseteq \mathrm{SL}(n,\mathbb{H})\).
The three Lie groups that are spheres: $$ S^0 \cong \{x \in
\mathbb{R}: \; |x| = 1\} = \mathrm{O}(1) \cong \mathbb{Z}_2 $$ $$ S^1
\cong \{x \in \mathbb{C}: \; |x| = 1\} = \mathrm{U}(1) \cong
\mathrm{O}(2) $$ $$ S^3 \cong \{x \in \mathbb{H}: \; |x| = 1\} =
\mathrm{Sp}(1) \cong \mathrm{SU}(2) $$
-
Part 5: Covers of Lie
groups, and universal
covers. The group \(\mathbb{R}\) is a universal cover of
\(\mathrm{SO}(2)\). The spin group
\(\mathrm{Spin}(n)\) is, by definition, the universal cover of
\(\mathrm{SO}(n)\) for \(n \ge 2\). Examples:
-
Spin(3) \(\cong \mathrm{SU}(2) \cong \mathrm{Sp}(1)\)
-
Spin(4) \( \cong \mathrm{SU}(2) \times \mathrm{SU}(2)\)
-
Spin(5)
\( \cong \mathrm{Sp}(2)\)
-
Spin(6) \( \cong \mathrm{SU}(4)\)
Proof that \(\mathrm{SO}(3)\)
is diffeomorphic to the projective space
\(\mathbb{R}\mathrm{P}^3\), which has fundamental group
\(\mathbb{Z}_2\). Proof that the
universal cover of \(\mathrm{SO}(3)\) is \(\mathrm{SU}(2)\).

Picture proof that the fundamental group of \(\mathrm{SO}(3)\) is \(\mathbb{Z}_2\): this is a fancy version of the belt trick.
Note that after the cube rotates 720°, the belts are back to their original positions!
-
Part 6: Compact
Lie groups. The Lie groups \(\mathrm{O}(n), \mathrm{SO}(n),
\mathrm{Spin}(n), \mathrm{U}(n), \mathrm{SU}(n)\) and
\(\mathrm{Sp}(n)\) are compact. The unfeasibility of classifying all
compact Lie groups. The classification of compact connected
Lie groups. Every compact connected Lie group has a finite cover that
is a product of a compact connected abelian Lie group and a
compact simply connected Lie group. Every compact connected
abelian Lie group is isomorphic to a torus
$$\mathbb{T}^n = \mathrm{U}(1) \times \cdots \times \mathrm{U}(1).$$
Every compact simply connected Lie group is isomorphic to a product of
finitely many copies of the classical compact
Lie groups \(\mathrm{Spin}(n), \mathrm{SU}(n), \mathrm{Sp}(n)\) and
the five exceptional
compact Lie groups, built using octonions:
- G2, the automorphism group of the octonions, which is 14-dimensional.
- F4, the isometry group of the octonionic projective plane, which is 52-dimensional.
- E6, the isometry group of the bioctonionic projective plane, which is 78-dimensional.
- E7, the isometry group of the quateroctonionic projective plane, which is 133-dimensional.
- E8, the isometry group of the octooctonionic projective plane, which is 248-dimensional: the king of Lie groups!
Example: \(\mathrm{U}(n)\) has \(\mathrm{U}(1) \times \mathrm{SU}(n)\) as an \(n\)-fold cover.
-
Part 7: Lie group actions. Transporting an action along
diffeomorphisms. Restricting an action to a closed subgroup.
-
Part 8: Felix Klein's idea for
reducing geometry to group theory: his Erlangen program.
Euclidean geometry and the Euclidean group.
The product of actions; restricting an action to an invariant
submanifold. Transitive
actions. How a Lie group gives a geometry and an action gives a
type of figure. Real projective
plane geometry and the group \(\mathrm{GL}(3,\mathbb{R})\):
points, lines and point-line flags. Higher-dimensional real projective
geometry and the group \(\mathrm{GL}(n,\mathbb{R})\): Grassmannians
and flag
manifolds. Complex
projective geometry and \(\mathrm{GL}(n, \mathbb{C})\), quaternionic
projective geometry and \(\mathrm{GL}(n,\mathbb{H})\). For more,
see:
-
Part 9: Lie
group representations. A representation of a Lie group \(G\) on a
finite-dimensional vector space \(V\) amounts to the same thing as a
Lie group homomorphism \(\rho \colon G \to \mathrm{GL}(V)\) where
the general linear
group \(\mathrm{GL}(V)\) is the Lie group of all invertible linear
transformations of \(V\). For any Lie group \(G\) there is a category
\(\mathrm{Act}(G)\) of actions of \(G\) and a subcategory
\(\mathrm{Rep}(G)\) of representations of \(G\). Example: the
tautological representations of \(\mathrm{GL}(n,\mathbb{R}),
\mathrm{GL}(n,\mathbb{C})\) and closed subgroups of these groups. The
direct sum and tensor product of representations. Proof that given a
representation \(\rho \colon G \to \mathrm{GL}(V)\) we have
$$ \rho \otimes \rho \; \cong \; S^2 V \, \oplus \Lambda^2 V $$
where \(S^2 V \subseteq V \otimes V\) is the space of symmetric tensors
and \(\Lambda^2 V \subseteq V \otimes V\) is the space of antisymmetric
tensors. The example of this where \(\rho\) is the tautological
representation of \(\mathrm{GL}(2,\mathbb{C})\) on \(\mathbb{C}^2\).
Definition of invariant subspace and subrepresentation.
A tiny taste of Young diagrams.
-
Part 10: Lie groups in quantum physics.
Hilbert
spaces. In quantum physics any system is described using some
Hilbert space \(H\), and the states of that system are described by
unit vectors \(\psi \in H\), that is, vectors \(\psi\) with \(\|\psi\|
= 1\). A linear operator \(U \colon H \to H'\) that maps unit vectors
to unit vector is called an isometry, and this is the
same as a linear operator that preserves the norm, or the inner
product. An invertible isometry is called a unitary operator.
A linear operator \(U \colon H \to H\) is unitary iff \(UU^\ast =
U^\ast U = 1_H\), and for any a Hilbert space \(H\) the unitary
operators
$$ \mathrm{U}(H) = \{ U \colon H \to H : \; U \textrm{ is unitary} \}
$$
form a Lie group. Any finite-dimensional Hilbert space
\(H\) is isomorphic to \(\mathbb{C}^n\) with its standard inner
product, and then \(U(H) \cong \mathrm{U}(n)\) is a Lie group. A
unitary
representation of a Lie group \(G\) on a finite-dimensional
Hilbert space \(H\) is a Lie group homomorphism \(\rho \colon G \to
\mathrm{U}(H)\). Examples: the spin-0 particle, the
spin-1/2 particle,
and the spin-1 particle are unitary representations
$$ \alpha_0 \colon \mathrm{SU}(2) \to \mathrm{U}(\mathbb{C}^1) \cong
\mathrm{U}(1) $$
$$ \alpha_{1/2} \colon \mathrm{SU}(2) \to \mathrm{U}(\mathbb{C}^2) \cong
\mathrm{U}(2) $$
$$ \alpha_1 \colon \mathrm{SU}(2) \to \mathrm{U}(\mathbb{C}^3)
\cong \mathrm{U}(3) $$
Rotating a spin-1 particle. How tensor products of representations describe ways of 'sticking
together' physical systems to build new physical system. When we
stick together two spin-1/2 particles we can get either a spin-0
particle or a spin-1 particles, due to the isomorphism of
representations $$ \alpha_{1/2} \otimes \alpha_{1/2} \cong \alpha_0
\oplus \alpha_1 $$ which arises from the isomorphism $$ \rho \otimes
\rho \; \cong \; \Lambda^2 V \, \oplus S^2 V. $$
-
Part 11: Lie algebras: a quick
overview of some essential facts which we will study in more detail
later. The Lie algebra \(\mathfrak{g}\) of a Lie group \(G\) is its
tangent space at the identity. There's a one-to-one correspondence
between elements \(v \in \mathfrak{g}\) and Lie group homomorphisms \(C
\colon \mathbb{R} \to G\), given by the requirement that \(C'(0) =
v\). The Lie algebra \(\mathfrak{g}\) acquires, in a manner to be
explained later, an operation $$ [\cdot,\cdot] : \mathfrak{g} \times
\mathfrak{g} \to \mathfrak{g} $$ that is bilinear, antisymmetric and
obeys the Jacobi
identity. Conversely, any finite-dimensional vector space with an
operation with these 3 properties arises (up to isomorphism) by taking
the tangent space of some Lie group \(G\). Furthermore, this Lie
group is unique (up to isomorphism) if we require that it's
connected and simply connected.
-
Part 12: The exponential map. For
any Lie group \(G\) and any \(v \in \mathfrak{g}\) there exists a
unique Lie group homomorphism \(C \colon \mathbb{R} \to G\) such that
\(C'(0) = v\). We prove this for matrix Lie groups using the
matrix
exponential: the exponential of an \(n \times n\) complex matrix
\(A \in M_n(\mathbb{C})\) is defined by
$$ \exp(A) = \sum_{n = 0}^\infty \frac{A^n}{n!} $$
and we get the Lie group homomorphism \(C \colon \mathbb{R} \to G\)
by setting
$$ C(t) = \exp(t v). $$
Our proof also uses the basic theorem on the local existence and uniqueness
of solutions of first-order ordinary differential equations.
-
Part 13: The Lie bracket. How
the Baker–Campbell–Hausdorff
formula lets us recover the product in a matrix Lie group, at least near
the identity, from the Lie bracket. Proof that if \(\mathfrak{g}\) is
the Lie algebra of matrix Lie group \(G\) then $$ v, w \in
\mathfrak{g} \implies vw - wv \in \mathfrak{g}. $$ In this case we can
start with the smooth map
$$ \begin{array}{rccl} \mathrm{AD}(g) \colon & G & \to & G \\
& h & \mapsto & ghg^{-1}
\end{array}
$$
for each \(g\in G\), then differentiate it to get
$$ \begin{array}{rccl} \mathrm{Ad}(g) \colon & \mathfrak{g} & \to
& \mathfrak{g} \\
& w & \mapsto & gwg^{-1}
\end{array}
$$
and then differentate this with respect to \(g\) to get a linear map
$$ \begin{array}{rccl} \mathrm{ad}(v) \colon & \mathfrak{g} & \to
& \mathfrak{g} \\
& w & \mapsto & vw - wv
\end{array}
$$
for each \(v \in \mathfrak{g}\). Thus, in this case we have an operation
\( [\cdot, \cdot] \colon \mathfrak{g} \times \mathfrak{g} \to \mathfrak{g} \)
given by
$$ [v,w] = vw - wv .$$
We define the Lie bracket for a general Lie group by copying this procedure:
we start with
$$ \begin{array}{rccl} \mathrm{AD}(g) \colon & G & \to & G \\
& h & \mapsto & ghg^{-1} ,
\end{array}
$$
then we differentiate it to get
$$ \mathrm{Ad}(g) \colon \mathfrak{g} \to \mathfrak{g} $$
and
$$ \mathrm{ad}(v) \colon \mathfrak{g} \to \mathfrak{g}, $$
and then define
$$ [v,w] = \mathrm{ad}(v)(w) . $$
Proof that the Lie bracket is linear in each argument, antisymmetric
and obeys the Jacobi identity.
-
Part 14: Matrix Lie algebras, also called
classical
Lie algebras. The Lie algebras of \(\mathrm{GL}(n,\mathbb{C}),
\mathrm{GL}(n, \mathbb{R})\) and \(\mathrm{GL}(n,\mathbb{H})\) are
$$ \mathfrak{gl}(n,\mathbb{C}) = \mathrm{M}_n(\mathbb{C}) $$
$$ \mathfrak{gl}(n,\mathbb{R}) = \mathrm{M}_n(\mathbb{R}) $$
$$ \mathfrak{gl}(n,\mathbb{H}) = \mathrm{M}_n(\mathbb{H}) $$
The Lie algebras of \(\mathrm{SL}(n,\mathbb{C}), \mathrm{SL}(n, \mathbb{R})\)
and \(\mathrm{SL}(n,\mathbb{H})\) are
$$ \mathfrak{gl}(n,\mathbb{C}) = \{a \in \mathrm{M}_n(\mathbb{C}): \mathrm{tr} (a) = 0\} $$
$$ \mathfrak{gl}(n,\mathbb{R}) = \{a \in \mathrm{M}_n(\mathbb{R}): \mathrm{tr} (a) = 0\} $$
$$ \mathfrak{gl}(n,\mathbb{H}) = \{a \in \mathrm{M}_n(\mathbb{H}): \mathrm{tr} (a) = 0\} $$
where in the last case we define a complex-valued trace of an \(n \times n\) quaternionic matrix by regarding it as a \(2n \times 2n\) complex matrix.
The Lie algebras of \(\mathrm{U}(n), \mathrm{O}(n)\) and \(\mathrm{Sp}(n)\) are
$$ \mathfrak{u}(n) = \{a \in \mathrm{M}_n(\mathbb{C}) : a + a^\ast = 0 \} $$
$$ \mathfrak{o}(n) = \{a \in \mathrm{M}_n(\mathbb{R}) : a + a^\ast = 0 \} $$
$$ \mathfrak{sp}(n) = \{a \in \mathrm{M}_n(\mathbb{H}) : a + a^\ast = 0 \} $$
A matrix with \(a + a^\ast = 0 \) is called skew-adjoint.
Finally, the Lie algebras of \(\mathrm{SU}(n)\) and \(\mathrm{SO}(n)\) are
$$ \mathfrak{su}(n) = \{a \in \mathrm{M}_n(\mathbb{C}) : \mathrm{tr}(a) = 0,
a + a^\ast = 0 \} $$
$$ \mathfrak{so}(n) = \mathfrak{o}(n) = \{a \in \mathrm{M}_n(\mathbb{H}) : a + a^\ast = 0 \} $$
where the final surprise happens because \(a + a^\ast = 0\) implies \(\mathrm{tr}(a) = 0\) for real matrices.
-
Part 15: From Lie groups to Lie
algebras. Every Lie group homomorphism gives a homomorphism of Lie
algebras. This defines a functor from the category
of Lie groups to Lie algebras, so our big commuting diagram of Lie
groups from Part 4 gives a big
commuting diagram of Lie algebras.
-
Part 16: Lie algebra
representations. How a Lie group representation \(\rho\colon G \to
GL(V)\) gives a Lie algebra representation \(d\rho \colon \mathfrak{g}
\to \mathfrak{gl}(V)\), and a unitary Lie group representation
\(\rho\colon G \to U(H)\) gives a Lie algebra representation \(d\rho
\colon \mathfrak{g} \to \mathfrak{u}(H)\).
-
Part 17: Lie algebras in quantum
mechanics. In quantum physics, self-adjoint
operators on the Hilbert space of a system correspond to observables. Given a
unitary representation \(\rho \colon G \to U(H)\) of a Lie group on a
finite-dimensional Hilbert space, we get an observable
\(id\rho(v) \colon H \to H\) for each element \(v \in \mathfrak{g}\).
How to compute the probability that we get a specific answer when we
measure some observable in some state. Example: the \(z\) component
of angular momentum for the spin-1/2 particle.
-
Part 18: A many-faceted Lie algebra. The
following Lie algebras are all isomorphic:
-
\(\mathfrak{o}(3) = \{a \in \mathrm{M}_3(\mathbb{R}) : \, a^\ast = -a \} \)
-
\(\mathfrak{so}(3) = \{a \in \mathrm{M}_3(\mathbb{R}) : \, a^\ast = -a,
\mathrm{tr}(a) = 0 \} \)
-
\(\mathfrak{su}(2) = \{a \in \mathrm{M}_2(\mathbb{C}) : \, a^\ast = -a, \mathrm{tr}(a) = 0 \} \)
-
\(\mathfrak{sp}(1) = \{a \in \mathbb{H} : \, a^\ast = -a \} \)
-
\(\mathbb{R}^3\) with its cross product as Lie bracket.
The isomorphism \(\mathfrak{sp}(1) \cong \mathfrak{su}(2)\) maps the
imaginary quaternions \(i,j,k\) to skew-adjoint matrices $$ I = \left(
\begin{array}{cc} 0 & -i \\ -i & 0 \end{array} \right) ,\quad J =
\left( \begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array} \right) , \quad K
= \left( \begin{array}{cc} -i & 0 \\ 0 & -i \end{array} \right). $$
Physicists turn these into self-adjoint matrices by multiplying them by
\(i\), and call the resulting self-adjoint matrices the Pauli matrices
\(\sigma_1, \sigma_2, \sigma_3 \).
-
Part 19 - The spin-1 particle.
Why the angular momentum of a spin-1 particle along the \(z\)
axis can only equal \(1, 0\) or \(-1\). The spin-1/2 particle revisited:
why the angular momentum of a spin-1/2 particle along the \(z\) axis
can only equal \(+\frac{1}{2}\) or \(-\frac{1}{2}\).
-
Part 20 - Irreducible
representations of Lie groups. Invariant subspaces,
subrepresentations,
reducible and
decomposable
representations. In what follows we consider only
finite-dimensional representations of Lie groups.
Every decomposable representation is reducible, but not conversely:
there is a 2-dimensional representation of the Lie group
\(\mathbb{R}\) that is reducible but not decomposable. However, every
unitary representation that is reducible is decomposable. Every
representation of a Lie group is a direct sum of finitely many
indecomposable representations. Every representation of
a compact Lie group can be given an inner product making it
unitary. Putting these results together, we see that every
representation of a compact Lie group is the direct sum of
finitely many irreducible representations.
-
Part 21: Irreducible
representations of SU(2). There is a representation
of \(\mathrm{SU}(2)\) on \(S^n \mathbb{C}^2\), which is the space of
homogeneous polynomials of degree \(n\) in two variables. If we set
\(j = n/2\), physicists call this the spin-\(j\) representation
$$ \alpha_j \colon \mathrm{SU}(2) \to \mathrm{GL}(S^n \mathbb{C}^2) $$
and it generalizes the cases we've already seen, where \(j = 0,\frac{1}{2}\)
and \(1\). We construct the spin-\(j\) representation and prove that
it is irreducible. The proof involves first building a representation
$$ \rho \colon \mathrm{GL}(2,\mathbb{C}) \to \mathrm{GL}(S^n \mathbb{C}^2),$$
and then restricting it to get the representation \(\alpha_j\) of
\(\mathrm{SU}(2)\). To prove this is irreducible it helps to show any
representation of \(\mathfrak{su}(n)\) on a complex vector space extends
to a representation of \(\mathfrak{sl}(n,\mathbb{C}\). In particular
$$ d\alpha_j \colon \mathfrak{su}(2) \to \mathfrak{gl}(S^n \mathbb{C}^2) $$
extends to a representation
$$ d\tilde{\alpha}_j \colon \mathfrak{sl}(2,\mathbb{C}) \to
\mathfrak{gl}(S^n \mathbb{C}^2) $$
which is a restriction of
$$ d\rho \colon \mathfrak{gl}(2,\mathbb{C}) \to
\mathfrak{gl}(S^n \mathbb{C}^2) $$
This lets us use raising and lowering operators on \(S^n \mathbb{C}^2\), also
called ladder operators. For other proofs, see:
-
Part 22: From \(\mathrm{SU}(2)\) to
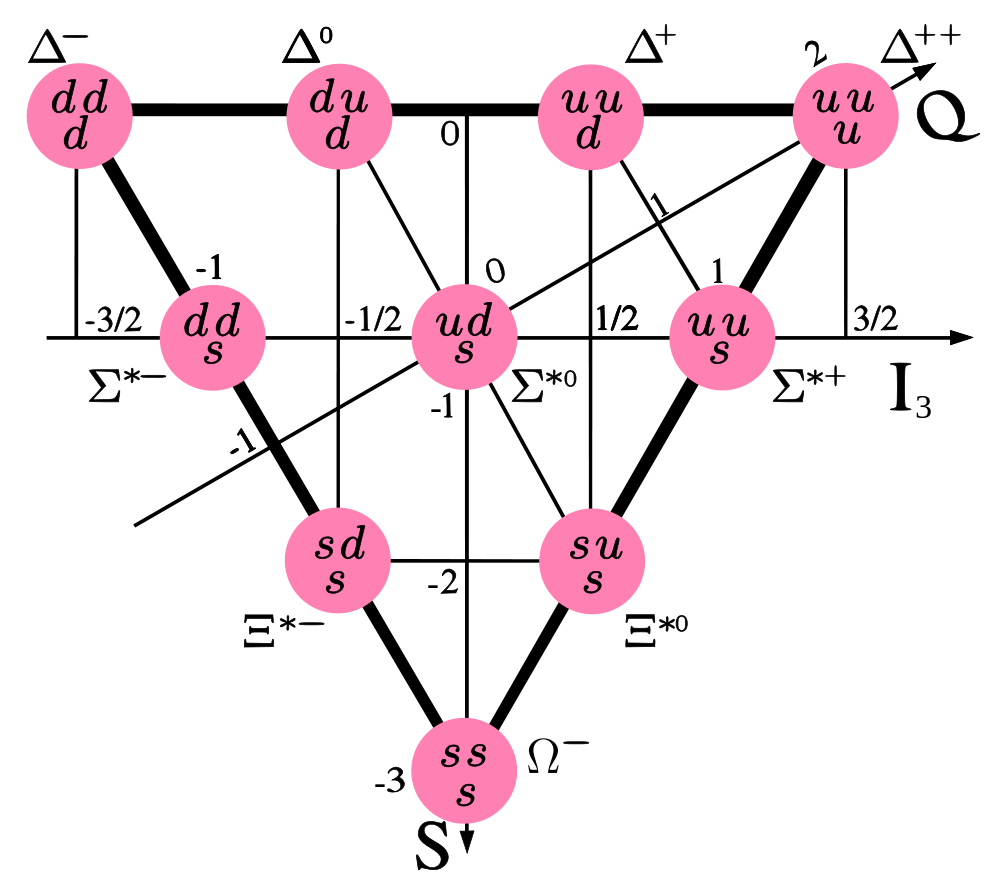
\(\mathrm{SU}(3)\) and beyond. Isospin and
representations of \(\mathrm{SU}(2)\). Gell-Mann's theory of quarks
and
representations of SU(3).
-
Part 23: Lie groups rule the world!
A reminder of how symmetries give observables. Time translation gives
energy; spatial translations give momentum; rotations give angular
momentum. Spatial translations and rotations can be combined into the
6-dimensional Euclidean group,
which has an action on space, \(\mathbb{R}^3\). Time translations and
the Euclidean group can be combined into a 7-dimensional Lie group
that has an action on spacetime, \(\mathbb{R}^4\). This group is a
subgroup of an even larger group that acts on spacetime, the
10-dimensional Galilei
group. The Galilei group also includes symmetries called boosts,
which give another important observable: position. Einstein's special
relativity replaces the Galilei group with another 10-dimensional Lie
group acting on spacetime: the Poincaré
group. In the Standard Model of
particle physics, the symmetry group is the product of the
Poincaré group and
$$ \mathrm{SU}(3) \times \mathrm{SU}(2) \times \mathrm{U}(1). $$
Here \(\mathrm{SU}(3)\) is the symmetry group
of the strong force, \(\mathrm{SU}(2)\) is the symmetry group of the
weak force and \(\mathrm{U}(1)\) is the symmetry group of the
electromagnetic force (roughly).